土结构性本构模型研究综述
2017-03-08刘帅帅柳艳华李丹梅
刘帅帅,柳艳华,李丹梅
(长安大学 公路学院,陕西 西安 710054)
土体的结构性,是指土颗粒和孔隙的性状和排列形式(或称组构)及颗粒之间的相互作用。绝大部分天然土体都具有结构性,较强的结构特性对土体的强度与变形影响显著,可以说土的结构性是决定各类土力学特性的一个最为根本的内在因素[1]。要想合理反应土体的应力应变关系,就必须对其结构性有正确的认识。而实际上目前大部分本构模型是针对饱和重塑土或者砂土建立起来的,天然土体本身具有的结构特性,导致用于工程计算时,产生较大的偏差。也正如我国学者沈珠江所提出的建立土体结构性的数学模型,是21世纪土力学的核心问题[2]。
研究土结构性问题的根本目的在于揭示结构性及其变化的力学效果[3]。谢定义[1]指出,当前关于土体结构性研究主要有三大基本途径:①基于微结构形态学的研究方法。它是借助光电量测技术,着重分析微观下土体颗粒或颗粒小团体在荷载作用下的变化规律,定量描述土体变形、破坏、蠕变等的作用原理,然后进行微结构力学效应分析,建立土体变形、强度等宏观变量与微观结构的关系。②基于固体力学的研究方法。它是从数学力学的观点出发,借助连续体损伤力学(CDM)、扰动状态理论等,建立一种能够有效反应土体在荷载作用下应力应变关系的力学模型。③基于土力学的研究方法。随着饱和重塑土的力学理论越来越成熟,对原状土与饱和重塑土进行试验研究,通过对比分析,从而引进表征土体结构性的参数来建立相应的结构性模型。本文简单介绍了近10年来提出的比较有代表性的土结构性本构模型,根据当前关于土结构性研究的三大基本途径对其进行分类,指出这些模型的特点以及在应用中可能存在的问题。最后,针对当前土结构性本构模型的发展趋势提出了几点建议。
1 土结构性本构模型
根据以上有关土体结构性研究的三大基本途径,从不同的理论基础及建模思路把当前土的结构性本构模型分为四类:(1)微观结构模型;(2)基于损伤理论和扰动状态理论建立的复合体损伤模型;(3)基于结构性参数建立的弹塑性本构模型;(4)利用边界面塑性理论建立的结构性本构模型。
1.1 微观结构本构模型
一直以来,从微观层面研究加载过程中结构性的变化,建立微观结构破损与宏观土体力学之间的联系,推出相关的应力应变关系,是研究土体结构性的一种有效途径。施斌等[4]从微观的角度考虑,基于土体速率过程理论,建立了表征黏性土各向异性和蠕变的微观力学模型,同时给出了蠕变的应力应变关系为:
σij=ηijkmεkm
(1)
式中,ηijkm为土体四阶黏滞张量。
蒋明镜等[5]通过对天然黏土室内压缩试验的离散元模拟,在微观层面上得出了土体结构的破损规律,采用函数来表示。同时改进了修正剑桥模型的硬化规律,提出了新的结构性土硬化规律表达式。其表达式为:
(2)

从微观角度对土体结构性进行分析,探究土体在受力过程中,其强度与变形发生变化的内在机理,这对于从宏观上揭示土体的工程特性具有重要的意义。通过这种方法建立的模型,作用机理和建模思路相对清晰,但是土体微结构复杂多样,目前大部分的微结构模型还处于理论分析阶段,距离工程应用还有一定的距离。且土体微观结构特征主要依靠光电测试技术进行研究,测试费用昂贵,现阶段还无法普遍推广。
1.2 复合体损伤模型
复合体损伤理论认为可以将原状土当作是初始无损伤且黏聚性强的胶结元和完全破坏后无胶结性的摩擦元复合而成的二元结构体。在实际荷载作用下土体逐渐发生破损并由胶结元慢慢转化为摩擦元,通过此演化过程来模拟土的结构性破坏。沈珠江[9]率先利用这种理论,将在荷载作用下的黏土抽象为大小不同的易碎土块的集合体,提出了考虑结构性的黏性土堆砌体模型,并推导出其相应的应力应变关系。其将损伤力学的理论引入到土力学中,为土结构性本构模型的研究开辟了新的途径。刘汉龙等[10]在已建立的软土三维弹塑性本构模型屈服函数中,引入沈珠江的结构性损伤因子及损伤复合体概念,基于统一各向同性准则,推导得出了结构性软土的三维弹塑性本构方程。其本构模型的增量表达式为:
{dεepd}={dε0}+{dεd}= (1-ω)·{dεep}+{dεd}
(3)
式中,{dεd}为损伤塑性变形,{dε0}为未发生损伤软土的弹塑性变形。
刘恩龙等[11]在岩土损伤力学的理论框架下,考虑土体初始应力下的各向异性,基于对结构性土破损机制的微观分析,引入了考虑初始各向异性的破损率λ和局部应变系数C,并给出了其宏观的表达式,建立了结构性土增量形式的二元介质(胶结元和摩擦元)模型。由于土体微结构的复杂性,目前还无法通过室内测试技术测定试样的破损参数,通常假定其为应力或应变的函数,并通过拟合室内单元试验结果来获取函数中所需要的相关参数。针对目前室内测试技术的局限性,蒋明镜等[12]以离散元法(DEM)为理论基础,对结构性黄土离散元试样进行增减荷和加湿的数值试验,给出离散元试样中所定义的破损参数b和B的表达式,并从数值试验中获得破损参数b和B的演化规律,建立了其与宏观力学特性之间的关系。之后,胡海军等[13]采用了上述离散元数值试验的方法,得到了理想结构性黄土离散元试样在加载和增湿过程中结构性破损参数的演化规律,将破损参数的函数形式引入到应力分担形式的二元介质(胶结元和摩擦元)本构模型当中去,并编制了数值计算程序与试验结果进行模拟对比分析。事实证明,此种方法测定的破损参数要比沈珠江建立的破损参数变化规律更为合理。
以损伤理论为基础建立土结构性本构模型,其优势是能够简单直接地描述土体结构的破损过程,其核心是损伤参数的选取和测定以及损伤规律的建立。但是,损伤理论并不能描述土体在损伤过程中出现强度软化后又增强的现象,针对这一不足,扰动状态概念理论(DSC)应运而生,它由美国学者C.S.Desai[14]提出,扰动函数D不但可以表征材料的损伤同时也可以描述材料的强化,从而弥补了损伤理论存在的缺陷。Ahad[15]对结构性土体的压缩特性进行研究,将初始屈服时的结构性土体视为相对完整状态,采用弹性理论来描述;完全破坏后的土体(重塑土)视为完全调整状态,采用修正剑桥模型进行描述。基于试验和理论构建扰动状态函数来反应土体在这两种状态演化过程中结构性损伤对压缩曲线的影响,从而建立相应的压缩模型。Desai模型中认为土体的扰动只包括偏应变扰动,这与实际还存在的体应变扰动不符。对此国内学者邵帅等[16]基于扰动状态理论和试验,将扰动因子分别定义为体应变扰动因子与偏应变扰动因子,并分别构建了体应变扰动函数和偏应变扰动函数,同样采用修正剑桥模型来描述土体的完全调整状态,提出了Q3结构性黄土的本构模型。其扰动状态下的增量方程为:
(4)
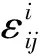
此模型相对于其他的基于扰动状态理论建立的模型来说,形式相对简单,参数容易测定,具有较好的实际工程应用前景。于小军等[17]借助电阻率不规则因子来进行扰动变量的表征和测试,改善了传统扰动状态变量获取方法的缺陷。通过三轴排水试验研究,构建了体应变扰动函数和偏应变扰动函数,来描述土体从相对完整状态转化为完全调整状态的动态过程,建立结构性软黏土的本构模型。
由于缺乏合适的设备,传统的扰动状态变量获取方法还不够完善,存在一定的缺陷和不足,这也成为阻碍基于扰动状态理论建立模型的一大因素,需要进一步深化研究。此外由于该类模型中往往参数众多,且不易在试验中直接获取,使得模型真正应用于实际工程尚有一定的困难。
1.3 基于结构性参数建立的弹塑性本构模型

(5)
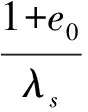
(6)
式中,F的定义如上式所示,λs为结构性黄土的压缩斜率;e0为土的初始孔隙比;M为等结构性临界状态线的斜率;psx为结构性黄土的屈服面与p轴的交点;pt=ccotφ;c为结构性黄土的黏聚力、φ为结构性黄土的内摩擦角;a1和b1为土性相关的材料参数。邓国华等[20]考虑到目前大多数的结构性参数;如最具代表性的应变结构性参数和应力结构性参数只能分别反映平均正应力和剪应力对土体结构性的影响,基于此,作者等在综合结构势理论的框架内,提出了既能反映平均正应力作用又能反映剪应力作用的应力比结构性参数mη,通过对天然黄土进行常规的三轴剪切试验,分析结构性黄土的强度特性,并提出了随着结构性参数变化的临界状态线的表达式,最后在修正剑桥模型的基础上建立了结构性黄土的本构模型。其模型的矩阵表达形式为:
(7)
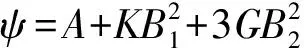
基于结构性参数建立的弹塑性本构模型,关键是结构性参数的表征和测定,往往依托大量的室内试验分析结构性参数与土体强度变形之间的关系,对试验的精确性具有严格的要求。修正剑桥模型由于理论基础严密,模型简单,参数易测,在其基础上进行结构性的修正以建立相应的本构模型,便于理解与推广。而依托临界状态理论,将传统的弹塑性模型扩展到结构性土的应用中去,通过土体结构强度的变化考虑结构性的影响,原理简单,易于理解。
1.4 利用边界面塑性理论建立的结构性本构模型
传统塑性理论认为土体在屈服面之内的应力状态只有弹性变形产生,这与实际变形中弹、塑性同时发生的情况相违背。而边界面塑性理论的提出便很好地弥补了这一局限性。将定义土体结构性的方法引入到边界面模型中,能够更加合理的描述土体的弹塑性变形和结构性损伤过程。M.Rouainia等[23]通过研究发现天然软黏土的屈服面要大于重塑土的屈服面。基于运动硬化的三面(结构边界面、气泡屈服面以及参考面)模型,以重塑土的屈服面为参考面,定义结构性损伤参数rd(pc/p0=rd),构建了rd的损伤演化规律:
(8)
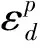
(9)
式中各参数的定义为:
(10)
(11)
(12)
(13)
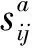
模型通过各向异性张量aij及其旋转硬化规律[24]来描述土体的各向异性,并定义重塑土的各向异性屈服面为参考面,通过对结构性黏土的试验结果进行模拟,验证了模型的合理性。柳艳华等[25]考虑到循环荷载极其复杂加载条件下结构性土的力学特征,又对上述模型进行了改进。将传统固定的映射中心改为可移动的映射中心,卸载时,映射中心不再固定在应力空间的坐标原点而是移至卸载起始点,在加载和卸载过程中采用不同的塑性模量表达式,来反映卸载—再加载过程中所产生的应变对应力的滞后性。
借助边界面塑性理论建立的模型,能够反映土体在循环荷载等复杂应力加载作用下的力学特性,也能够很好地描述土体在变形过程中出现的软化现象。但是其缺点是本构方程过于复杂,模型参数较多,且部分物理意义模糊,不易通过室内试验获取。总之,将模型应用在实际工程中有较大的困难。
2 结论
本文基于结构性研究的三大途径及不同的建模思路,对近10年提出的土结构性本构模型进行分类,总结评价,指出了模型的特点及存在的不足,并得出以下结论:
(1)目前对于土体结构性破损规律多是从宏观角度进行研究,缺少从微观层面研究加载过程中结构性的变化。鉴于此,随着试验量测技术和有限元计算软件的快速发展,应加强从微观层次的研究,分析结构性土体受力后微观结构变化的内在机理,正确的表征微观变量与宏观力学特性之间的联系,提出更加合理的本构模型。
在本构模型中,如何合理的确定模型参数对模型的应用有着至关重要的影响。目前采用室内土工试验确定的模型参数往往与实际现场中差异较大。所以,研究室内试验确定的模型参数与实际现场环境下参数之间的对应关系也是下一步工作的重点。
(3)研究本构模型的目的是为了能更好地服务于实际工程。因而,应更多地关注于模型的适用性、参数求取的简易性。
[1] 谢定义,齐吉琳.土结构性及其定量化参数研究的新途径[J].岩土工程学报,1999,21(6):651-656.
[2] 沈珠江.土体结构性的数学模型-21世纪土力学的核心问题[J].岩土工程学报,1996,18(1):95-97.
[3] 谢定义.试论我国黄土力学研究中的若干新趋向[J].岩土工程学报,2001,23(1):3-13.
[4] 施斌,王宝军,宁文务.各向异性黏性土蠕变的微观力学模型[J].岩土工程学报,1997,19(3):7-13.
[5] 蒋明镜,刘静德,孙渝刚.基于微观破损规律的结构性土本构模型[J].岩工程学报,2013,35(6):1134-1139.
[6] 蒋明镜,周卫,刘静德,等.基于微观力学机制的各向异性结构性砂土的本构模型研究[J].岩土力学,2016.(12):3347-3355.
[7] FANG H L,ZHENG H,ZHENG J.Micromechanics-based Multimechanism Bounding Surface Model for Sands[J].International Journal of Plasticity,2017.
[8] PAUL G J.Physical Basis and Validation of A Constitutive Model for Soil Shear Derived from Microstructural Changes[J].International Journal of Geomechanics,2013,13(4):365-383.
[9] 沈珠江.结构性黏土的堆砌体模型[J].岩土力学,2000,21(1):1-4.
[10] 刘汉龙,肖杨,崔允亮.结构性软土三维弹塑性损伤本构模型研究[J].岩土工程学报,2011,33(4):637- 642.
[11] 刘恩龙,罗开泰,张树祎.初始应力各向异性结构性土的二元介质模型[J].岩土力学,2013,34(11):3103-3109.
[12] 蒋明镜,胡海军.荷载和水作用下结构性黄土破损规律的离散元分析[J].岩土工程学报,2014,36(6):989- 997
[13] 胡海军,蒋明镜.引入离散元所得破损规律的结构性黄土本构模型[J].岩石力学与工程学报,2016,(S1): 3241-3248.
[14] DESAI C S,Ma Y.Modelling of Joints and Interfaces Using the Disturbed State Concept[J].International Journal for Numerical and Analytical Methods in Geomechanics,1992,16(9):623-653.
[15] AHAD Q.Disturbed State Concept-based Constitutive Model for Structured Soils[J].International Journal of Geomechanics,2016.
[16] 邵帅,褚峰,邵生俊.Q3结构性黄土的扰动状态本构模型试验研究[J].岩石力学与工程学报,2016,35(7):1494 -1500.
[17] 于小军,齐志宏.基于扰动状态概念的结构性软黏土本构模型[J].岩土工程学报,2009,31(12):1882-1887.
[18] 谢定义,齐吉琳,张振中.考虑土结构性的本构关系[J].土木工程学报,2000,33(4):35-41.
[19] 罗爱忠,邵生俊,陈昌禄,等.黄土的湿载结构性本构模型研究[J].岩土力学,2015,36(8):2209-2215.
[20] 邓国华,邵生俊,佘芳涛.结构性黄土的修正剑桥模型[J].岩土工程学报,2012,34(5):834-841.
[21] 吴小锋,李光范,胡伟,等.海口红黏土的结构性本构模型研究[J].岩土力学,2013,(11):3187 -3191.
[22] LIU M D,CARTER J P.A Structured Cam-clay Model[J].Canadian Geotechnical Journal,2002,39(6):1313 -1332.
[23] ROUAINIA M,VOOD D M. A Kinematic Harding Constitutivemodel for Natural Clays with Loss of Structure[J].Geotechnique,2000,50(2):153-164.
[24] 魏星,黄茂松.天然结构性黏土的各向异性边界面模型[J].岩土工程学报,2007,29(8):1224-1229.
[25] 柳艳华,黄茂松,李 帅.循环荷载下结构性软黏土的各向异性边界面模型[J].岩土工程学报,2010,32(7): 1065-1071.
