波浪作用下独墩码头振动作用及其控制方法研究

郭廷凯，李 强

（浙江海洋大学船舶与机电工程学院，浙江舟山 316022）

码头结构在波浪等海上动力荷载作用下容易产生较大的动力响应，长期频繁的作用会导致结构引起疲劳损伤甚至破坏。因此，对码头结构受到波浪等海洋环境荷载作用下的研究就显得十分重要，对码头结构的设计乃至建成后的安全运营都有着重要的现实意义。

目前国内外有关波浪力对结构物的影响有大量的研究：HAN，et al[1]运用了Hamiliton原理和Kirchhoff假设研究了上端自由而下端支撑在海底条件下立管在波浪作用下的轴向与水平振动特性；黄津等[2]在工程实例的背景下，采用ANSYS软件建立高桩码头有限元模型，研究波浪力对高桩码头结构的影响，并对桩的失稳提出解决方案。杨长义等[3]以Morison方程为基础，采用不同的波浪理论计算了作用于高桩码头单根直桩和斜桩上的正向波浪力，研究结果发现：d/L≤0.2时，采用忽略波浪非线性因素的线性波计算得到的正向波浪力偏小，应采用Stokes五阶波进行计算。刘柞秋等[4]在波浪力的作用下对桩一土一承台随着承台所受外力、波浪力、桩侧地基土的变化进行研究，研究结果发现：采用相互作用模型分析桩一土一承台结构中桩和采用规范的计算结果几乎完全一致；在波浪力对桩的作用时，特别是在淤泥、粉砂中，波浪力对桩土承台结构影响较大。黄华定等[5]以金塘跨海大桥为背景开展了波浪对桥墩基础作用的研究。由于该桥址所在海域水流和波浪都比较大，实际情况比计算模型更为复杂，因此现场的实测数据是客观准确的，测试的主要内容是水流和波浪对桥墩基础的作用，实验测得的数据可作为桥梁设计的重要参数，而这些参数在设计规范里都没有明确的规定。

本文以舟山某浮式码头中的固定独立桩墩结构的工程存在的问题为背景，以分析与解决工程问题为目的，开展波浪作用下对独墩码头的动力响应研究，分析结构产生振动的原因并提出合理的抑制振动的方法，具有一定的工程应用价值。

1 工程背景与工程问题

1.1 工程背景

根据某码头工程实例为研究背景，该独墩码头由桥台墩、桩和土构成，码头下方共有9根圆柱桩支撑，分布方式是3×3布置，竖向和水平的每两根桩间距5 m，如图1所示；该码头的桥台墩采用混凝土材料，设计参数见表1；该码头桩墩由6根钢管桩支撑，钢管桩的截面直径D=0.8 m，为计算方便，将结构简化为二维平面模型，具体设计参数见表2。

图1 某独墩码头工程实况图Fig.1 Image of a single-pier wharf

表1 桩墩结构尺寸及材料参数Tab.1 Pile pier structure size and material parameters

表2 钢管桩尺寸及材料参数Tab.2 Steel pipe pile size and material parameters

根据本工程地质报告，在钻探所达深度范围内，场地地层层序如下：袋装碎石、淤泥粉质粘土、粉质粘土1、粉质粘土2、含砂砾粉质粘土、强风化花岗岩、中风化花岗岩、微风化花岗岩，见表3；该码头工程的设计流速和50 a一遇的极端波浪参数见表4。

表3 各类土体的尺寸及物理参数Tab.3 Size and physical parameters of all types of soil

表4 海洋环境参数Tab.4 Ocean environment parameters

1.2 工程问题与分析

该独墩式码头在投付使用后就出现了较为明显的振动现象，经过较长时间运营后振动愈加明显，且已经出现一定的应变累积，承台与固定式结构之间出现了永久性变位，进一步发展可能会影响正常使用。

通过现场踏勘，该水域的水流较急，波高较大，同时受船行波的影响较为明显。波浪作用是该独墩式码头出现上述问题的外因。而且，通过分析该码头在施工时采用的施工工艺，因该处的水流较急，打桩施工时为稳桩而采用了袋砂碎石抛填的方法，抛填厚度较大，但在设计时并未考虑由于该抛填产生的附加荷载对于下卧软土层的附加固结沉降作用。

为准确找出该桩墩结构振动原因，拟采用有限元方法建立桩墩在波浪作用下的动力响应分析模型，研究波浪作用对桩墩的振动影响，揭示其振动的原因。为进一步控制结构的振动，本文提出采用桩间加横联的方式进行控制，横联位置考虑设置低潮位上方0.5 m处，以方便施工加固。

2 有限元模型与数值分析

2.1 有限元计算原理与计算模型

本文运用有限元软件建立独墩码头的二维简化计算模型，研究独墩码头在波浪作用下的整体运动响应。

独墩码头在打桩施工时为稳桩而采用了袋装碎石抛填的方法，抛填厚度3 m，相当于在淤泥层上加了3 m厚度的袋装碎石，使下卧土层产生附加应力，导致淤泥固结和淤泥层压缩，从而加大了钢管桩的暴露长度。经过实地勘测验证，证实泥面标高下降3 m左右。针对这一问题，本文采用在码头平台高程不发生变化的情况下，只是使淤泥层单纯发生沉降进行设计工况,分别将淤泥层的厚度降低0、1、2、3 m的四种基本工况，并对降低3 m的模型中桩间架设横联也设置了一个工况进行对比研究。五种工况如下：

工况1：独墩码头沉降0 m（即独墩码头设计时的模型）；

工况2：独墩码头沉降1 m；

工况3：独墩码头沉降2 m；

工况4：独墩码头沉降3 m（即独墩码头现在的模型）；

工况5：独墩码头沉降3 m且在结构平潮位上方0.5 m处加横联；

将独墩码头结构离散为功能与原结构相当的二维有限元模型（图2），按照实际结构情况划分节点和单元，然后把全部的荷载等效为节点荷载作用在节点上，而节点由单元的刚度支持，进而计算节点的位移和应力，最后算出单元应力得到码头结构的变形状况[6]。

2.2 独墩码头模型计算参数的设置

以工况1的码头为例，独墩码头计算模型中，计算区域为广阔无垠土域中的一个长方形区域，长40 m，宽34.7 m，当静水时其浸水深度为10 m，来流条件为远方从左到右均匀一入射波动，其波动方程为 z=η（x,y）=H+A0cosk（x-ct），其中由码头工程概况中的海洋环境情况可知波长λ=61.2 m，振幅A0=4.02 m，远方均匀来流流速为1.5 m/s，则水波周期对桩体采用理想弹性体分析，土体采用理想弹塑性分析，假定服从Mohr-Coulomb屈服准则，但是在底层微强化花岗岩底层假设底床平整且无滑移固壁条件；左右两侧由于与水流流向平行且因至于广阔无垠的区域中，故设定为对称边界条件，其法向速度为0，设置为两端固定；对本码头模型进行网格划分；其中桩采用梁单元B21，桥台墩采用CPS4R实体单元，土体结构采用CPe4R实体单元。

在对独墩码头结构的动力响应分析中，波浪力对结构的影响十分重要的。对于波浪问题，受波浪作用的码头墩柱结构根据直径与波长的比值可以划分为小尺度和大尺度两类，其波浪理论和计算公式是不一样的，小尺度墩柱采用Morison公式[7]，大尺度墩柱采用绕射理论（也称为势流理论）[8]。本文中所涉及的某独墩码头工程，直径D与波长L的比值D/L＜0.2，属于小尺度结构，采用Morrison公式来计算结构的波浪力[9]。根据挪威船级社（DNV）规范，位于桩柱任意高度（距离海底以上高度d+z）处的水平波浪力fH按Morison方程计算如图3所示。

其受到的水平波浪力可以表示为阻力fD和惯性力fM之和，作用于单位长度直立圆柱上的波向力fH为:

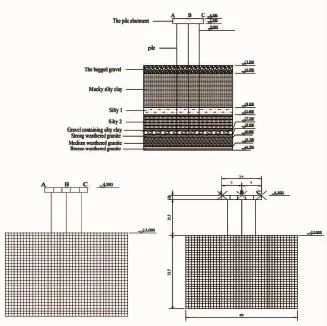
图2 典型工况示意图与有限元网格划分Fig.2 Schematic diagram of typical working conditions and finite element meshes

图3 小尺寸直立圆柱波浪力计算示意图Fig.3 Small size vertical cylinder wave force calculation schematic diagram

其中，θ=kx-ωt，在有限深水条件下有 ω2=gktanh（kd），将其带入 Morison 方程，考虑圆柱轴心上 x=0（即θ=-ωt），则单位圆柱上的水平波浪力:

其中Morison公式中的两个水动力系数CD和CM的取值关系到最后计算结果的正确性。国内外学者在大量规则波或震荡流对垂直桩柱作用力试验基础上，对这两个系数的取值作了规定[11-12]，给出了许多建议值。在本模型中，主要依据《海港水文规范JTJ213-98》[13]来确定来和，它们分别取为0.7和1.5。

3 计算结果与分析

为反映独墩码头结构在波浪作用下的动力响应，在工况1、工况2、工况3、工况4和工况5的桥台墩顶面左右两侧和中部相同的位置取了3个监测点（图2）。通过有限元计算对这三个监测点进行水平和竖向方向的振动情况进行分析，并与现场测量数据相对比，然后分析桩间架设横联对独墩码头振动的抑制作用。

3.1 不同的沉降深度对独墩码头的影响

由有限元软件计算经后处理可得到工况1—工况4独墩码头上三个监测点在波浪作用下的时间位移曲线（图4～6）。

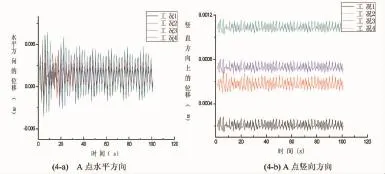
图4 监测点A的时间位移关系Fig.4 Time-displacement relationship of monitoring point A

图5 监测点B的时间位移关系Fig.5 Time-displacement relationship of monitoring point B

图6 监测点C的时间位移关系Fig.6 Time-displacement relationship of monitoring point C

从图4～6对比可以看出，四种不同工况下的A、B、C三个监测点的振动随着土层的固结沉降加大而增大。原设计工况1在A、B、C三个监测点的水平最大位移分别为0.002 3、0.002 5、0.002 9 m，竖向最大振动位移分别为0.000 21、0.000 22、0.000 34 m；当土层沉降达3 m时，A、B、C三个监测点的水平振动位移分别增大至0.007 5、0.007 7、0.007 8 m，竖向振动位移分别增大至 0.001 15、0.001 21、0.001 85 m；水平向振动位移增幅平均约为3倍；竖向振动位移增幅平均为5.45倍。

从图7可以看出，随着独墩码头的地层沉降，即桩结构在水中的暴露段逐渐增加，码头整体结构在水平方向和竖直方向的振幅呈非线性增长。如果独墩码头不发生地质沉降，从图中工况1数据可以看出，码头整体结构水平方向的振幅符合设计时的要求。但是因施工中所采用的抛石稳桩工艺，造成了土层的附加应力增加，从而产生地层沉降，加剧了独墩码头的振动。

图7 监测点水平和竖向振动最大位移与土层沉降值的关系Fig.7 The relationship between the maximum horizontal and vertical vibration displacement and the soil settlement

3.2 独墩码头工程的现场实测对比

在独墩码头现场进行了测量，主要用波谱器、恒流适配器、加速度传感器等仪器工具及WS-DAQ数据采集软件，进行低速数据采集，本次试验主要测量一段时间内在波浪作用条件下独墩码头的振动加速度的频率和振型。再从计算机上读取其数值并进行分析，推算出对应的相对位移，与数值模拟的。

由WS-DAQ数据采集软件处理可得到工况4独墩码头上三个监测点在波浪作用下的加速度曲线。将数值模拟工况4与现场测量的加速度进行比较，如图8所示。

图8 数值模拟工况4与现场测量的加速度比较图Fig.8 Comparison of acceleration between numerical simulation of condition 4 and field measurement.

从图8可以看出，数值模拟工况4与现场测量的加速度数据曲线基本比较吻合，说明独墩码头模型的数值模拟具有真实性与可靠性，为能够解决实际工程的设计与问题的解决提供了可靠地依据和保证。

3.3 架设横联对独墩码头振动的抑制作用分析

采用在桩间架设横联的方法来控制独墩码头的振动作用，根据有限元计算结果，对比了工况4（不加横联独墩码头）和工况5（加横联独墩码头）上A、B、C三个监测点在波浪作用下的时间位移曲线（图9）。

图9 未加横联与加横联支撑条件下独墩码头的振动位移的比较Fig.9 Comparison of vibration displacement between conditions with and without the cross-bracing

从图9可以看出，工况4在A、B、C监测点的水平最大位移分别为0.007 5、0.007 7、0.007 8 m，竖向最大位移分别为0.001 15、0.001 21、0.001 85 m，工况5在A、B、C监测点的水平最大位移分别为0.000 39、0.000 69、0.000 89 m，竖向最大位移分别为0.000 65、0.000 87、0.001 06 m；可见在独墩码头上架设横联的位移明显小于不加横联的情况，架设横联可以有效地抑制独墩码头结构的振动。

4 结论

本文在波浪作用下对独墩码头地层沉降不同深度的几个工况进行数值分析，并分析了采用架设横联来抑制振动的效果，得到如下结论：

二维简化有限元计算表明，随着独墩码头的地层沉降，桩在水中的暴露段逐渐增加，在波浪作用下桩墩结构在水平和竖向方向的振幅呈非线性增长，且水平位移比竖向位移大。

数值模拟的结果与现场实测基本吻合，采用数值模拟方法解决工程问题具有一定的可靠性。

对结构同一个位置的水平位移比较发现架设横联的要比未加横联的位移减小，大约减少了未加横联时的60%～80%的振幅；对竖向位移比较发现，加横联的要比未加横联时位移减少了40%～60%。说明架设横联对码头的独立桩墩具有明显的约束作用，可以取得良好的振动抑制效果。

[1]HAN S M,BENAROYA H.Non-linear coupled transverse and axial vibration of a compliant structure Part 1:Formulation and free vibration[J].Journal of sound and vibration,2000,237（5）:837-873.

[2]黄 津,于小存,陈志勇.波浪力对高桩码头结构的影响分析[J].港工技术,2010,47（3）:8-12.

[3]杨长义,陈玺文.浅析作用于外海高桩码头单桩上的正向波浪力计算[J].港工技术,2013,50（6）:15-18.

[4]刘祚秋,周翠英,温少荣,等.桩-土-承台结构在波浪力作用下的力学效应分析[J].岩土力学,2005,26（7）:1 109-1 112.

[5]黄华定,于旭东.金塘大桥波流力的分析研究[J].公路,2009（1）:127-129.

[6]MORISON J R,JOHNSON J W,SCHAAF S A,et al.The Force exerted by Surface Waves on Piles[J].Journal of Petroleum Technology,1950,2（5）:149-154.

[7]杨江辉,张 宏,刘锦昆,等.基于ABAQUS/AQUA的深水导管架平台动力分析研究[J].中国海洋平台,2007,22（6）:29-33.

[8]王献孚.计算船舶流体力学[M].上海:上海交通大学出版社,1992.

[9]戴 澍,解 德.基于ABAQUS的小尺度桩柱波浪力计算方法[J].固体力学学报,2011,32（增刊）:288-295.

[10]李远林.波浪理论及波浪载荷[M].广州:华南理工大学出版社,1994.

[11]丁 军,王登婷.基于边界元法大尺度柱体上的波浪荷载分析[C]//中国钢结构协会海洋钢结构分会2010年学术会议暨理事会第三次会议,2010.

[12]赵子丹,陆君良.微幅波对矩形竖直墩柱的作用[J].海洋学报:中文版,1980,2（3）:137-152.

[13]中华人民共和国交通部.海港水文规范（JTJ 213-98）[S].北京:人民交通出版社,1998.