基于贝叶斯压缩感知的自旋目标成像

蒙继东，尚 社

(中国空间技术研究院 西安分院，陕西 西安 710100)

基于贝叶斯压缩感知的自旋目标成像

蒙继东，尚 社

(中国空间技术研究院 西安分院，陕西 西安 710100)

窄带雷达受发射信号带宽限制，距离向分辨率低，通常应用于目标检测和跟踪。窄带雷达可通过转动目标的微多普勒对其进行精确成像，为目标识别提供新思路。文中在窄带雷达成像基础上，根据目标散射点稀疏性，提出了基于贝叶斯压缩感知的自旋目标成像算法。仿真结果表明，方位欠采样条件下，比复数后向投影算法得到的图像更加尖锐，因而具有更高的分辨率。且与传统压缩感知方法相比，需要更少的信号。

窄带雷达；微多普勒；贝叶斯压缩感知；自旋目标

对于一些尺寸较小的自旋目标，窄带雷达的带宽无法满足其ISAR成像需求。自旋目标在在一定姿态角范围内，对载波频率产生周期性调制，这种称为微多普勒效应[1]。近年来国内外关于利用微多普勒效应对旋转目标成像开展了广泛深入的研究工作[2]。文献[3]利用空间碎片自旋运动产生正弦分布的多普勒谱，提出了一种单距离多普勒干涉(SRDI)算法,实现对空间碎片的二维成像。文献[4]提出了单距离匹配滤波(SRMF)算法通过构造不同旋转半径下的匹配滤波器，分别对横向回波数据进行匹配滤波得到不同半径上点散射强度的估计从而可估计出目标的形状尺寸。SRMF利用快速傅里叶变换(FFT)有效地提高成像速率与SRDI算法相比具有分辨率高、计算量少的优点，但是受旁瓣影响，分辨率有限。文献[5]提出复数后向投影算法对旋转散射点的相位进行匹配搜索成像，当回波数据是欠采样的，图像比较模糊。基于压缩感知的正交匹配算法能精确重构图像，低信噪比(SNR)和高PRF情况下的回波，无法准确地重构所有目标散射点。

贝叶斯压缩感知[6]将统计学中的贝叶斯理论[7]与压缩感知理论[8]相结合，在相关向量机[9](RVM)框架下，求解得出原始信号或其稀疏权系数的最大后验估计，重构出原始信号值。本文将贝叶斯压缩感知应用于自旋目标成像[10-11]，提出了一种基于贝叶斯压缩感知的自旋目标成像算法。方位欠采样条件下，比后向投影算法得到的图像更加尖锐，因而具有更高的分辨率。且与传统压缩感知方法相比，在抗噪声和稀疏信号重构更有优势。

1 自旋目标的窄带雷达成像模型

自旋目标经过补偿转化为转台模型，且该目标在观测时间类转速恒定，图1给出窄带雷达自旋目标的成像模型。在直角坐标系XYZ中，雷达视线为y轴方向，目标旋转矢量为Ω，与雷达视线夹角为，目标散射点P在成像平面上的投影为P′。

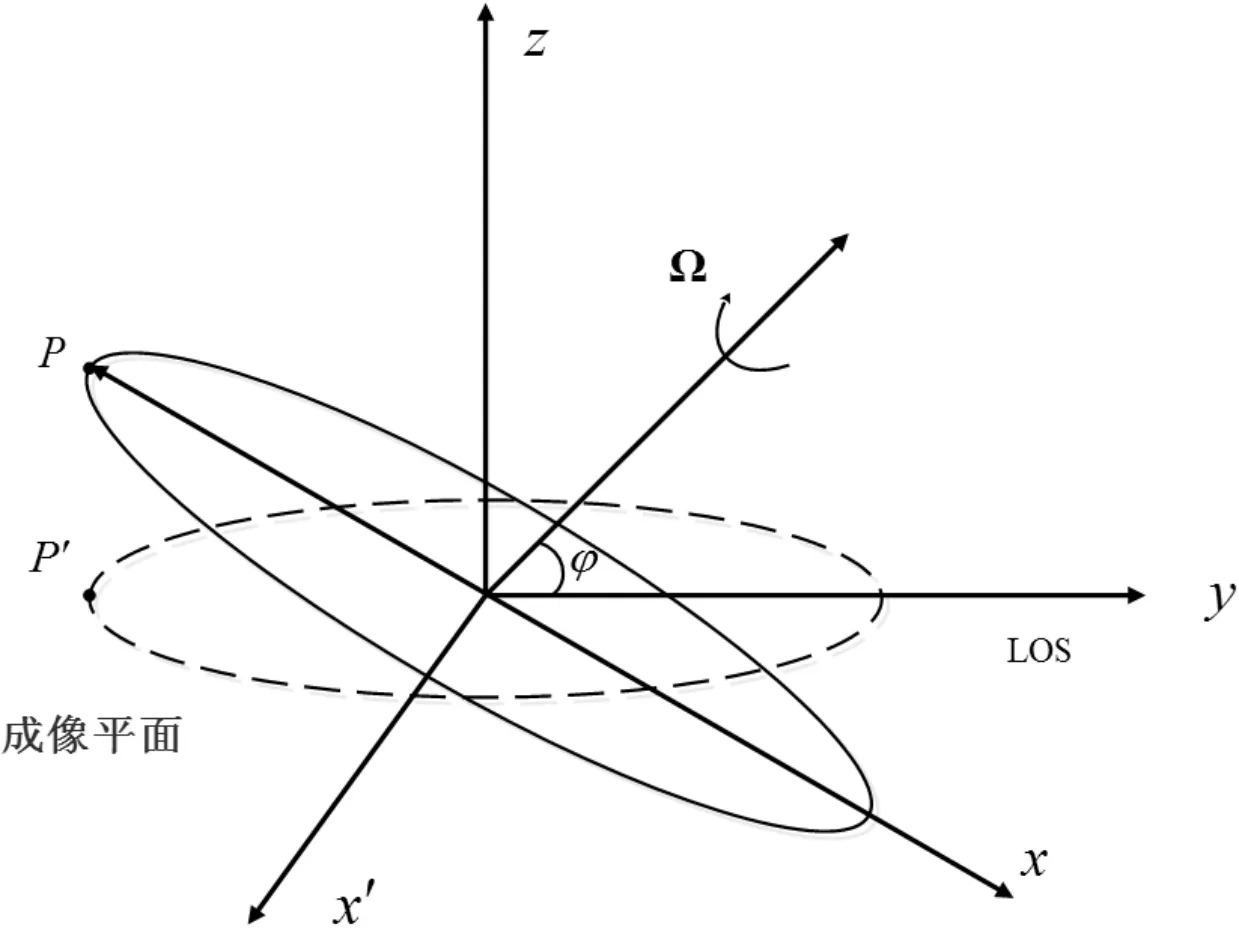
图1 自旋目标成像几何模型

对于窄带雷达，目标上第k个散射点的慢时间回波满足

(1)

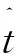
将回波与载波混频后，得到基带信号

(2)

其中，λ表示波长，λ=c/fc。根据图1成像模型，第k个散射点在旋转平面上的初始坐标为(xk,yk)，则Rk(tm)满足

(3)

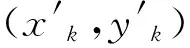
(4)

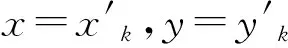
2 贝叶斯压缩感知的自旋目标成像

假设对于离散二维场景，距离向有X个散射位置，方位向有Y个散射位置，后向散射系数的非零散射点个数为K，则可将式(4)原始信号可稀疏表示为

(6)

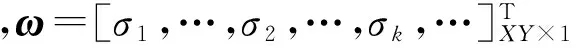
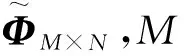
(7)

(8)

根据压缩感知理论

(9)

为求解式(9)，可采用贪婪算法或者凸优化算法[12]，该算法在低信噪比下，无法对散射系数精确求解。BCS能够提供散射系数的全后验概率密度估计，并考虑了压缩欠采样过程中的噪声，因而具有更好的鲁棒性。

YM×1方位向欠采样数据，nM×1高斯白噪声，均值为0，方差为σ2

(10)

目的是对散射ω和σ2作最大后验估计。为避免模型中参数和训练样本个数一样多而导致的严重过匹配问题，需要对参数加一定的约束条件，在贝叶斯框架下一般对参数指定先验分布作为其约束条件，较为常用的是Laplace分布

(11)

然而，在贝叶斯分析方法中，Laplace先验条件不能直接使用，因Laplace先验条件和高斯密度函数不是共轭的。为了解决这个问题，引入相关向量机理论(RVM)，采用分层先验的模型结构。对稀疏散射系数ω指定零均值的高斯先验分布，即

(12)

其中，αi，i=1,…,M是高斯分布方差的倒数，然后对α和α0分别附加Gamma先验分布

(13)

p(α0|c,d)=Γ(α0|c,d)

(14)

得到ω的后验概率密度函数

p=(ω|α,α0)=N(ω|μ,Σ)

(15)

其中，均值和方差分别为

μ=αΣΦTY

(16)

Σ=(α0ΦTΦ+Λ)-1

(17)

其中,Λ=diag(α1,α2,…,αM).

在贝叶斯框架下，边缘似然函数等效对数表达形式如

(18)

其中，C=σ2I+ΦA-1ΦT，利用期望最大化算法(Evidence Maximization, EM)或II型最大似然估计算法求解[13-14]

(19)

(20)

其中，γi=1-αi∑ii是量化因子。μ和Σ是α0和α的函数，同时α0和α是μ和Σ的函数，式(16)～式(17)与式(19)、式(20)形成了迭代[15]。当经过多次迭代运算，散射系数系数ω误差在允许误差范围内，即迭代收敛时，稀疏散射系数ω的重构估计值对应的就是后验均值μ。需要注意的是，贝叶斯压缩感知算法最初定义在实数域上，而方位向慢时间雷达信号和稀疏基均是复数据，因此，要对观测系统作如下的变换

(21)

3 仿真验证

为验证所提算法有效性，采用自旋目标仿真窄带雷达回波数据对两种算法性能比较。雷达中心频率为fc=10 GHz，对应波长为λ=0.03 m，系统带宽为B=30 MHz，对应距离分辨率为5 m。如图2所示，目标散射点分布为螺旋桨形状，后向散射系数均为1，散射点最大自旋半径为0.6 m，目标自旋角速率 。方位无模糊成像时所需的脉冲重复频率为10 053 Hz，观测时间0.2 s，方位向采样数为2 010。

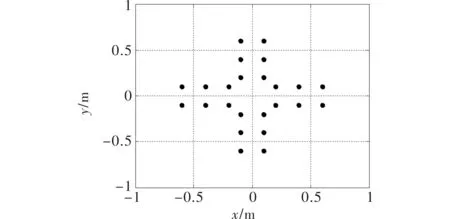
图2 仿真目标散射点分布

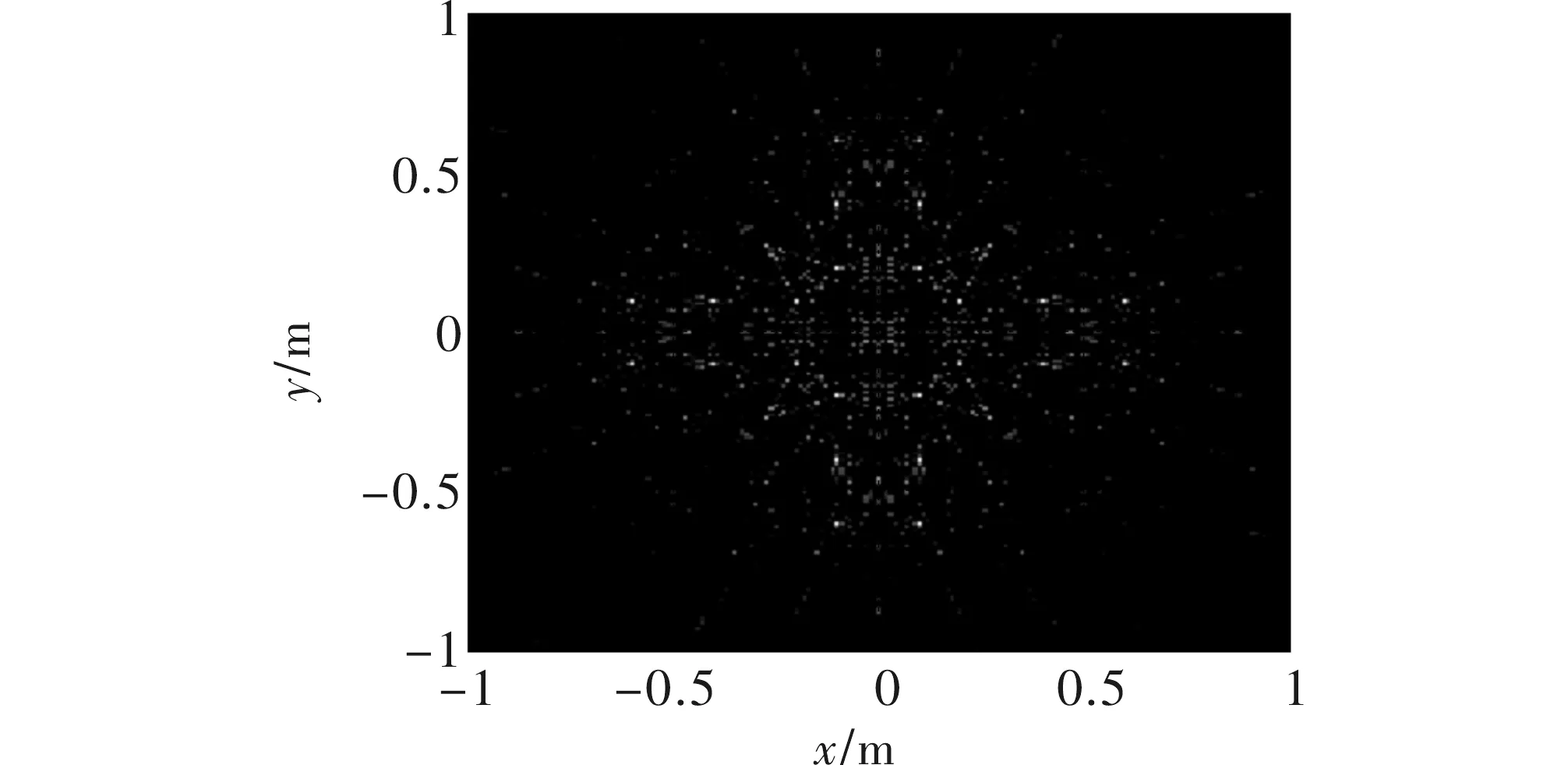
图3 复数后向投影算法得到图像

图3为信噪比10 dB时复数后向投影算法成像结果，从图中可看出准确地估计出散射点位置，当散射点距离较近时，受旁瓣影响易掩盖真实散射点同时产生较多的虚假散射点，降低图像质量。

图4和图5分别为CS算法和BCS算法在信噪比10 dB，方位向欠采样率为50%成像结果，均能准确地估计出散射点位置和后向散射系数，对比发现，CS算法产生较多虚假散射点，受方位欠采样率和噪声的影响。

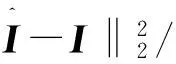
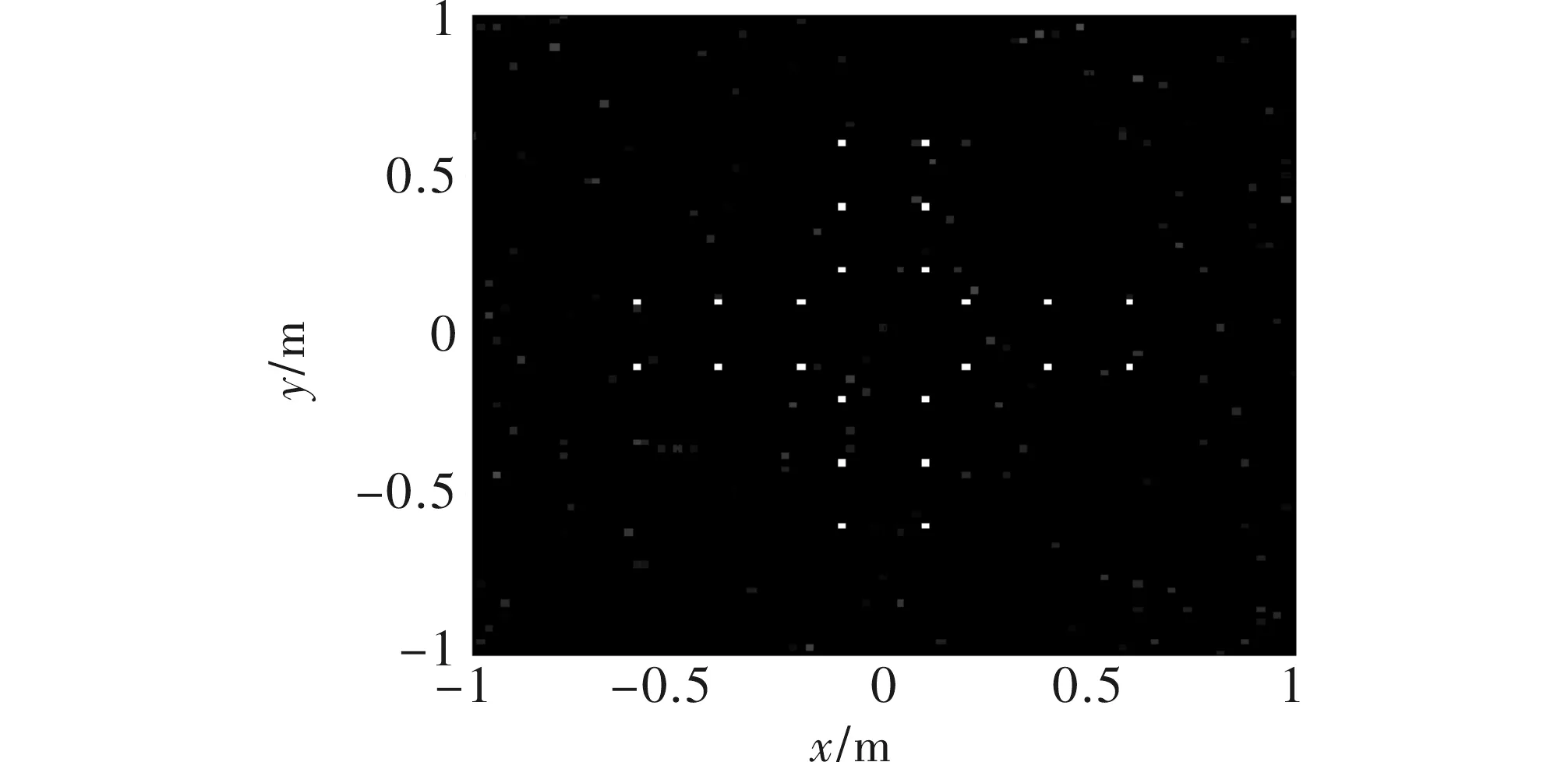
图4 CS算法图像

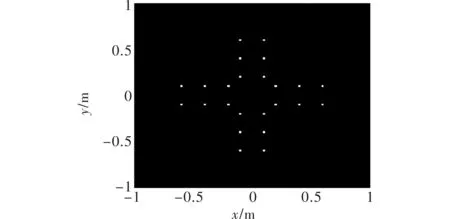
图5 BCS算法图像

图6为欠采样率50%条件下，两种算法随信噪比变化的性能曲线，可看出两种算法的归一化均方误差随信噪比提高逐渐降低，信噪比达到一定值后趋于稳定0。在相同信噪比条件下，BCS算法比CS算法误差小。信噪比达到一定值后，两种算法效果相同。图7为信噪比0 dB条件下，两种算法随欠采样率变化的性能曲线，出两种算法的归一化均方误差随欠采样率提高逐渐降低，欠采样率达到一定值后趋于稳定，BCS算法比CS算法误差小。对比图6和图7，在自旋目标成像中BCS算法比CS算法性能好。

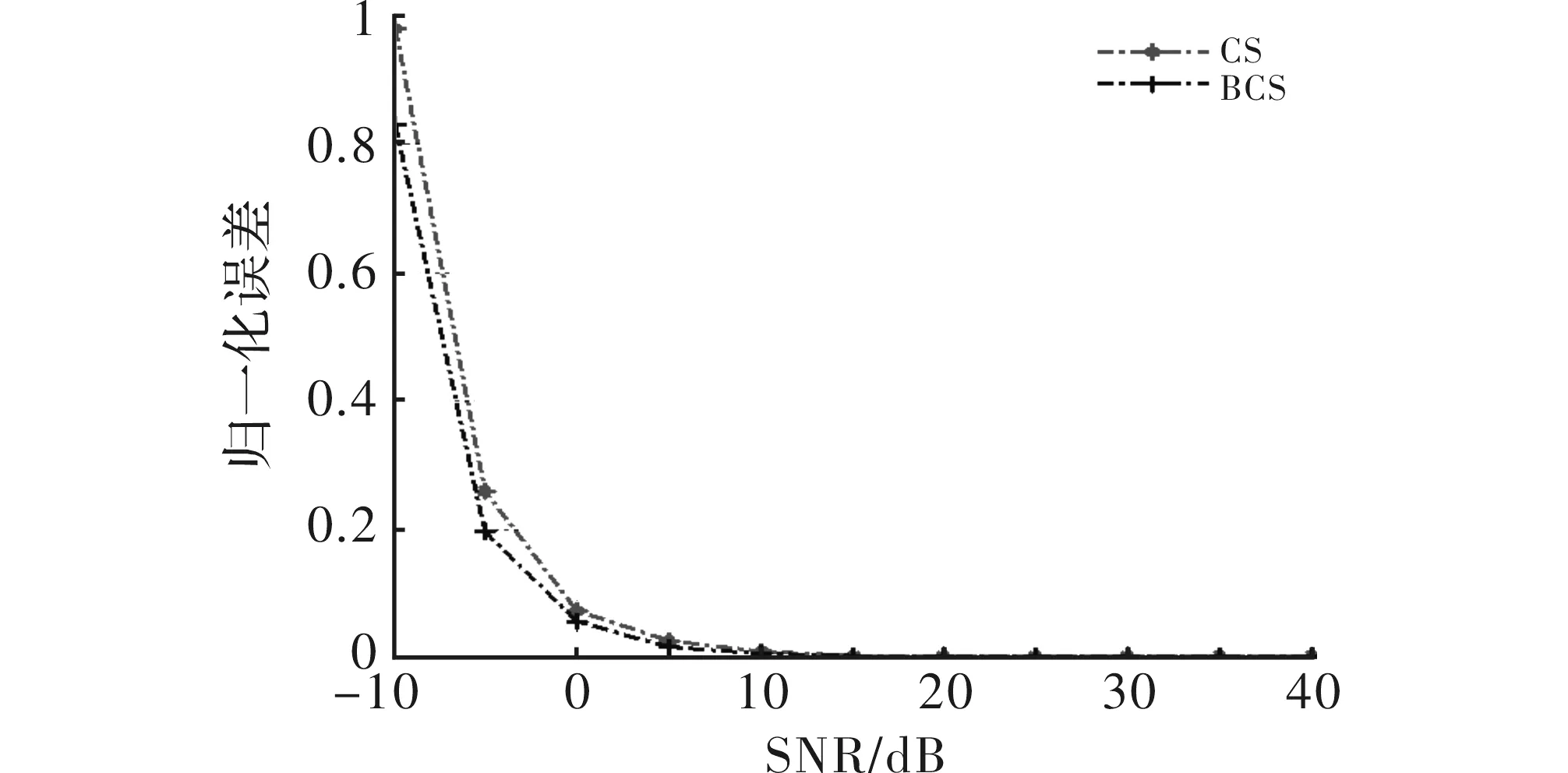
图6 归一化误差与信噪比的关系

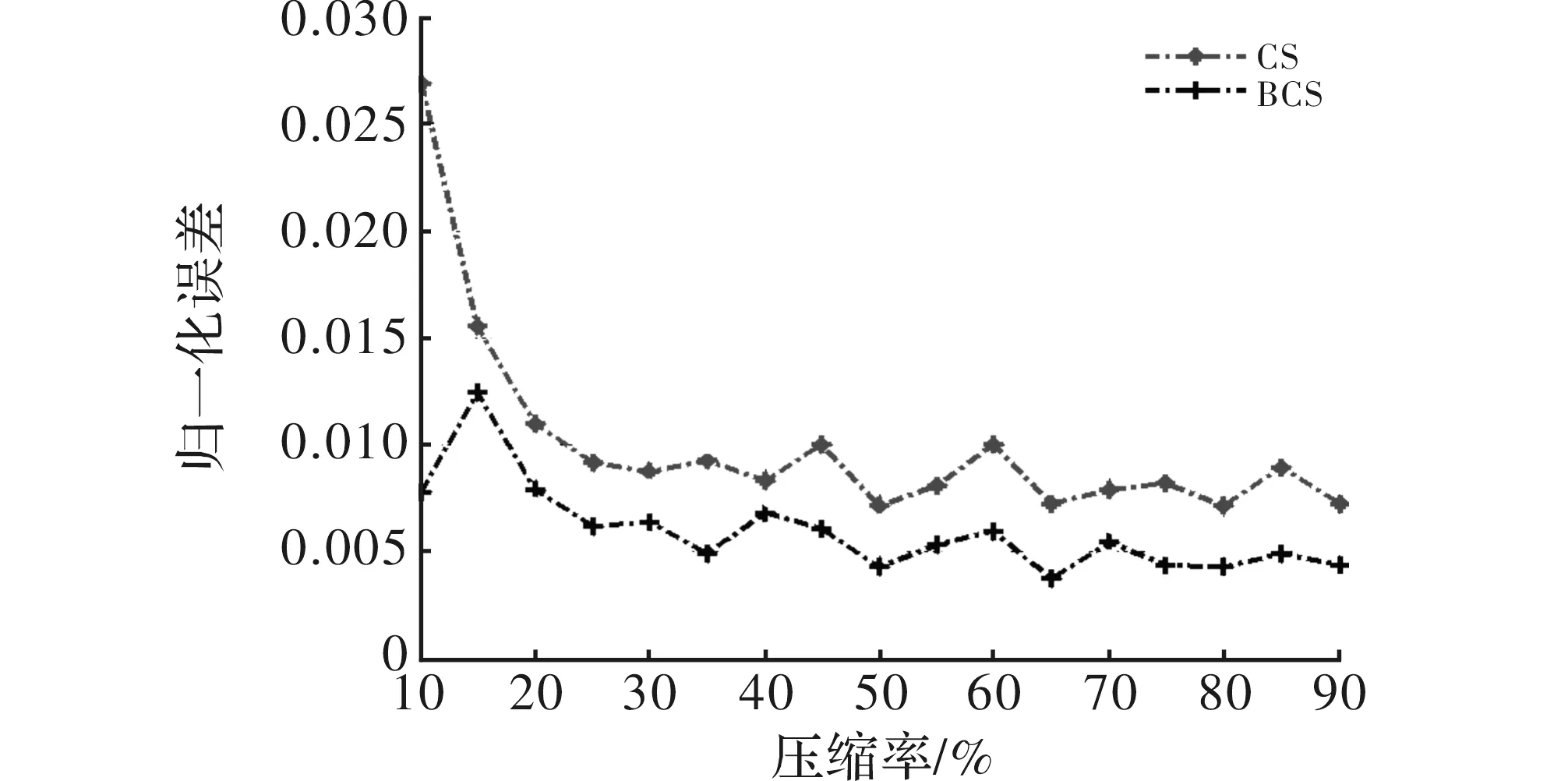
图7 归一化误差与压缩率的关系

4 结束语

本文以窄带雷达对自旋成像理论，针对复数后向投影算法受旁瓣分辨率有限，提出了基于贝叶斯压缩感知的自旋目标成像算法，大幅度提高成像分辨率，有利于目标识别。相比CS算法只能提供点估计，BCS能够提供散射系数的全后验概率密度估计，并考虑了压缩欠采样过程中的噪声，因而具有更好的鲁棒性。在不同条件下的仿真数据成像结果验证算法的有效性。

[1] Chen V C, Li F, Ho S S, et al. Micro-doppler effect in radar: phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(1):2-21.

[2] Chen V C,Ling H.Time-frequency transforms for radar imaging and signal analysis [M].Norwood, MA:Artech House,2002.

[3] Sato T.Shape estimation of space debris using single-range doppler interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(2):1000-1005.

[4] 王琦,邢孟道,保铮.基于单距离匹配滤波的太空碎片雷达成像[J].电子与信息学报,2008,30(5):1037-1040.

[5] 白雪茹,孙光才,武其松,等.窄带雷达自旋目标成像[J].中国科学:信息科学,2010(11):1508-1518.

[6] Ji S.Bayesian compressive sensing[J].IEEE Transactions on Signal Process,2008,7(56):2346-2356.

[7] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory, 2006,52(4):1289-1306.

[8] Oliveri G,Rocca P,Massa A. A bayesian compressive sampling-based inversion for imaging sparse scatterers[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(10): 3993-4006.

[9] Tipping M E.Sparse bayesian learning an-d the relevance vector machine[J].Journal of Machine Learning Research,2001,2(1):211-244.

[10] Ender J H G. On compressive sensing applied to radar[J].Signal Processing,2010,90(2):1402-1414.

[11] 谢晓春,张云华.基于压缩感知的二维雷达成像算法[J].电子与信息学报,2010,32(5): 1234-1238.

[12] Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010, 4(2):310-316.

[13] Derin Babacan S. Bayesian compressive sensing using laplace priors [J]. IEEE Transaction on Image Processing,2010,19(1):53-63.

[14] Faul A C,Tipping M E. Analysis of sparse bayesian learning[C].Paris:Advances in Neural Information Processing Systems, 2002: 383-389.

[15] 徐建平,皮亦鸣,曹宗杰.基于贝叶斯压缩感知的合成孔径雷达高分辨成像[J].电子与信息学报,2011, 33(12):2863-2868.

Spinning Target Imaging Based on Bayesian Compressive Sensing

MENG Jidong，SHANG She

(Xi’an Branch, China Academy of Space Technology, Xi’an 710100, China)

Narrow-band radar which emits the signal restricted by bandwidth limitation has a low resolution in range profile, so usually applies to target detection and tracking. Narrow-band radar can be imaged precisely by the rotating target’s micro-Doppler, providing a new idea of target recognition. Due to the characteristics of narrow-band radar echoes from spinning targets, an imaging method based on Bayesian compressive sensing (BCS) is proposed according to the sparsity nature of narrow-band radar echoes from spinning targets. Simulation results show that the proposed approach offers a sharp and sparse image absence of side-lobes which is the common problem in conventional complex-valued back-projection method imaging methods and has fewer artifacts than the conventional compressive sensing (CS) based methods.

narrow-band radar; micro-doppler; Bayesian compressive sensing; spinning targets

2016- 03- 28

蒙继东(1989-)，男，硕士研究生。研究方向：雷达探测与成像。

10.16180/j.cnki.issn1007-7820.2017.02.025

TN959

A

1007-7820(2017)02-094-04