面向轨迹预测的高超声速飞行器气动性能分析

翟岱亮，雷虎民，李海宁，周 觐

(1.空军工程大学 防空反导学院，西安 710051；2.95247部队，惠州 516000)

面向轨迹预测的高超声速飞行器气动性能分析

翟岱亮1，雷虎民1，李海宁2，周 觐1

(1.空军工程大学 防空反导学院，西安 710051；2.95247部队，惠州 516000)

为了给高超声速轨迹预测问题提供先验知识，研究了面向轨迹预测的高超声速飞行器气动性能分析问题。首先，简要介绍了高超声速再入滑翔飞行器的基本性能，从拦截的角度分析了对其滑翔段进行轨迹预测的必要性。其次，以HTV-2为例，采用斜激波理论、活塞理论、Prandtl-Meyer方程及粘性力工程计算方法对临近空间高超声速环境下飞行器的受力情况进行了分析建模。然后，对目标机动性能进行了仿真分析，仿真结果与相关文献报道较一致，证明了建模仿真方法的可行性。最后，基于以上建模仿真，给出了一组适用于临近空间高超声速飞行器滑翔段目标跟踪和轨迹预测的气动参数，并进行了仿真验证，为下一步研究基于拦截的高超声速飞行器轨迹预测提供了理论基础和方法指导。

高超声速飞行器；轨迹预测；气动力；滑翔；HTV-2

0 引言

高超声速再入滑翔飞行器(Hypersonic Reentry-glide Vehicle,HRGV)一般是指飞行马赫数大于5，能利用自身特殊的气动外形提供升力在临近空间进行无动力滑翔飞行，执行全球快速打击任务的飞行器[1-2]。它具有机动能力强、弹道灵活多变、难于拦截等诸多优点，受到了高度重视。目前，各军事大国对HRGV的控制特性[3-4]、动力学特性[5-6]、轨迹优化[7]、热防护[8]及跟踪[9]等问题进行了大量研究，而对于HRGV的拦截问题鲜有报道。

由于目标飞行速度很高，只能采用预测命中点法进行制导拦截，这就对目标的轨迹预测提出了很高的要求。预测问题的实质就是要获知至少两个方面的信息：参量的当前状态分布和参量的变化规律，对于目标的轨迹预测而言，即为目标当前飞行状态和目标运动模型。通过目标跟踪，可获得目标的当前状态；而要获知目标未来时刻的运动模型，需要充分的掌握关于目标的先验知识，包括目标的作战运用方式、机动方式、机动范围以及过去时刻的飞行规律等。目前，对高超声速飞行器机动性能的相关研究较少，文献[10]仅分析了高超声速滑翔飞行器的机动能力，文献[11]仅对高超声速飞行器的转弯半径进行了研究。

在滑翔阶段，目标飞行时间最长、受力影响因素最少，是防御的主要阶段。本文重点以此飞行阶段为研究对象，从飞行器的受力分析入手，以HTV-2为例，研究目标的机动性能和气动参数，为进行目标跟踪和目标轨迹预测研究提供先验知识。另外，精确的高阶状态转移模型总是伴随着高度的非线性，会增加数据处理难度和估计精度，本文在临近空间目标气动力计算和机动性能分析的基础上给出了一组适用于HRGV跟踪和预测的近似线性化参数，为目标轨迹预测提供了可能。

1 目标模型

1.1 目标运动模型

本文使用东北天坐标系(East-North-Up CS，ENUCS)描述目标状态，则HRGV的运动模型可表示为

(1)

其中

(2)

(3)

因此，只需对g和uk进行建模描述，即可对目标的轨迹及机动性能进行定量分析。重力加速度模型可按照地球建模的详细程度，分为平面地球模型、球面地球模型和椭球地球模型，这里采用最简单的重力模型，将地球视为平面，则在ENUCS下，有：g=[0 0 g]T。气动加速度uk将采用下一节气动力计算方法进行建模，为此首先给定如下信息：

(1) 目标质量

假设目标质量为450kg。

(2) 坐标转换

(4)

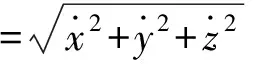
(3) 大气模型和声速模型

气动力计算还需要大气密度与声速等大气数据模型。标准大气表是以实际大气特征的统计平均温度值为基础，并结合一定的近似数值计算所形成的。这里采用美国1976年标准大气的计算方法。

1.2 目标简化几何模型

由于无法获得HTV-2的具体几何模型参数，为了获取对目标气动性能的定量分析，用如图1所示的近似简化模型进行仿真分析。

HTV-2简化模型的几何参数如下：

顶点：p1(4,0,0)、p2(0,1,0)、p3(0,0.5,0.5)、p4(0,-0.5,0.5)、p5(0,-1,0)、p6(0,0,0)。

表面：s1(p1,p5,p2)、s2(p1,p2,p3)、s3(p1,p3,p4)、s4(p1,p4,p5)、s5(p5,p4,p6)、s6(p4,p3,p6)、s7(p6,p3,p2)。

2 气动力计算方法

随着计算机软硬件技术的发展和计算流体力学(CFD)研究的不断深入，CFD软件已广泛应用于飞行器的气动力分析，且可靠性较高。但通常CFD软件计算法方法复杂，对计算机的性能要求较高；另一方面，采用CFD软件不利于气动相关参数的分析。因此，本文采用高超声速环境下飞行器气动力的工程计算方法进行目标机动性能分析[5-6,12]。高超声速飞行器飞行高度位于临近空间，飞行速度Ma>5，其所处大气环境和所受气体动力学规律均与低空低速飞行目标不同。假定一个具有方向的理想平面，其法线方向表示为dsurf=(xsurf，ysurf)，设气流速度方向为dsteam=(xsteam，ysteam)，根据几何关系，可将气流偏转角定义为

(5)

则气流偏转角为正时，气流被压缩；当气流偏转角为负时，气流膨胀，如图2所示。

2.1 迎风面压强

计算压缩气流对表面的压强，可采用不同的方法，如Bolender使用激波斜激波理论，Chavez使用牛顿碰撞理论，Oppenheimer的活塞理论。这里以斜激波理论为主，遇到不可解的情况时，改用活塞理论。

(1) 斜激波理论

采用斜激波理论求解气流被压缩之后的压强，需要一个中间数据，即激波角θs。激波角定义为气流方向到激波面的转角。

斜激波的压强p与激波角θs有关：

(6)

式中p∞为自由流压强；M∞为自由流马赫数；γ为气体的比热容，理想气体γ=1.4 。

激波角可用以下方程进行求解：

(6)

其中

(8)

设s=sin2θs，令f(s)=s3+bs2+cs+d，则δ取不同的值时，函数f(s)随s的变化曲线如图3所示。图中，δ较小时，曲线位于下侧；δ较大时，曲线位于上侧；并且对于所有的s=0，f(s)<0；对所有的s=1，f(s)>0。由曲线可知，在气流转折角较小时，具有3个根，其中最小根为减熵根，最大根也舍去，取曲线在下降段的根作为激波角。

利用牛顿迭代法解斜激波关系式时，为了避免遇到非物理解，可将初值设为曲线拐点，也即d2f(s)=0处，有

(9)

利用此参考初值，即可保证迭代解法的收敛性。

(2) 活塞理论

观察图2中的一系列曲线，发现在δ大于某一定值时，方程仅有一个非物理根，此时斜激波理论不可用，定义此δ为“最大有效气流偏转角δeff”。经由多次仿真，发现δeff与马赫数正相关，然而解析形式尚未查明，这里拟用一组仿真数据(如表1所示)拟合，拟合曲线如图4所示。

从图4可看出，在M∞≥5时，最大气流转折角变化不大，使用M∞=5时的值。M∞<5时采用拟合值，为保守起见，δmax少取3°，则

(5)

当压缩角δ>δeff时，斜激波理论不再适用，转而采用活塞理论。活塞理论认为飞行器表面上某一点的压强p仅与该点的下洗速度有关，类似活塞在一维管道中运动时所有压强与其运动速度的关系：

(11)

式中Vn为当地下洗速度；a∞为当地音速。

又因为

(12)

故

(13)

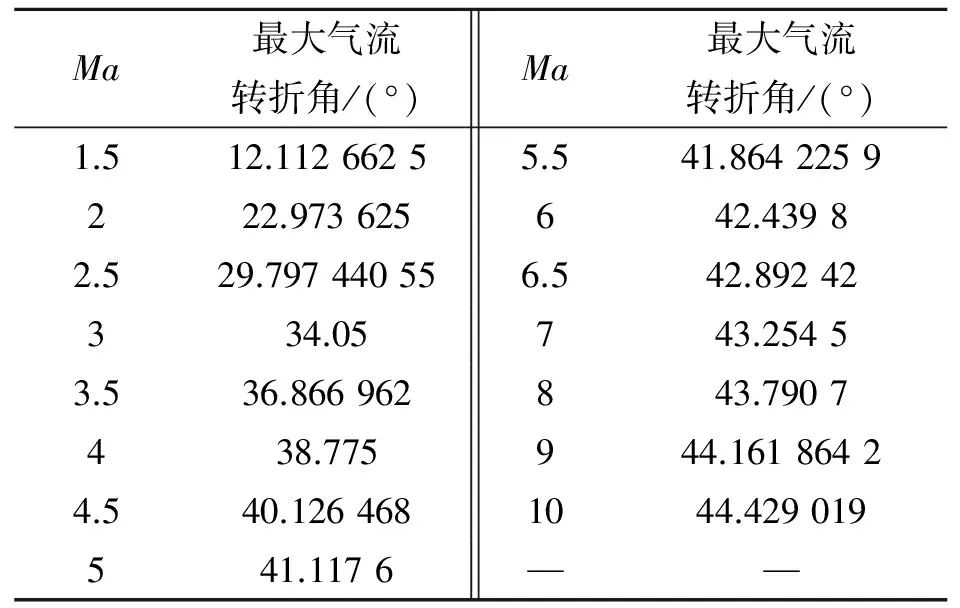
表 1 最大气流偏转角

用活塞理论得到的压强曲线在马赫数约为3时是基本连续的，在马赫数更高的情况下是不连续的。与斜激波理论相比，用活塞理论得到的压强更高，但与斜激波理论得到的压强处于一个量级。

2.2 背风面压强

在高超声速条件下，此过程气流加速、减压。在解算气流膨胀的压强时，一个重要的中间量是膨胀后的马赫数M1，可用Prandtl-Meyer方程求解：

(14)

其主要部分的形式为

(15)

它随马赫数的变化曲线如图5所示。

从图5可看出，v(M)是有限度的，最大值约为130°。将M∞带入式(11)右侧，再加上气流膨胀角δ，可能会大于130°，使方程无解。解决的办法是在解算之前判断方程右侧的值，若超过极限值，则将其替代为一个小于但接近极限值的角度，此角度仍然对应着极高的马赫数和极低的压强比，背风面附近区域接近真空，仍然与真实情况接近。另外，在马赫数较低时，v(M)曲线并不单调，因此应保证飞行器速度在Ma=1.5以上。

解得马赫数之后，即可使用等熵流关系式得到膨胀波的压强：

(16)

2.3 粘性力计算

由于在高超声速环境下，粘性对飞行器的气动性能和推进性能等的影响显著。文献[12]采用粘性力工程计算方法对高超声速飞行器所受的粘性力进行计算，结果与CFD基本一致。则飞行器上下表面的粘性力可表示为

(17)

式中ρ、v和μ分别为机体表面流体的密度、速度和粘性系数；L为机体沿气流方向长度。

3 目标运动性能分析

3.1 目标气动力分析

对HTV-2的简化模型采用Bolender等给出的三维机体高超声速气动力估算方法进行计算，即可得到不同条件下的气动性能。HTV-2在30 km高度，不同马赫数的流场中的升阻比(标量)随攻角变化曲线如图6所示。通过仿真验证，发现飞行器的最大升阻比与马赫数正相关。各马赫数条件下，最大升阻比出现在攻角约8.6°时，马赫数在5～20之间时推测其升阻比介于3.5～5之间，这与相关文献报道论述[1-2]相一致。

3.2 目标机动能力分析

为保证足够的飞行距离，假设飞行器在整个过程中按最大升阻比(即攻角为8.6°)飞行。另根据文献HTV-2滑翔段主要在30～60 km飞行，马赫数在3～20范围，这里给定飞行器初始状态s0=[0 0 60 km 6.8 km/s 0 0]T，倾侧角在0°～36°范围内不同取值条件下，目标的三维轨迹如图7所示。从图7可见，目标的最大纵向飞行距离大于10 000 km，最大横向机动距离可达5 000 km，这也是与文献报道较为吻合的。

3.3 目标机动参数分析

进行目标气动力和轨迹分析的目的是为后续目标跟踪[9]和轨迹预测提供先验知识，这就需要充分分析影响目标机动性能的参数。

飞行器的在VTCCS下的气动加速度aVTC是空气压强和气动参数α的函数，这里表示为

(18)

为了使气动力用线性化参数表示，通过仿真试验，这里给出一组VTCCS下的新气动参数αVTC，它与目标在VTCCS下加速度的关系可表示为

(18)

式中p∞为自由流压强；v为目标速度。

为进一步验证本文提出的气动参数的性能，通过文献[13]中的再入体运动方程对其进行试验。给定初始状态s0=[0 0 40 km 2.4 km/s 0 0]T，假设目标按以下2种机动方式飞行：

机动方式1：攻角按幅度分别为6.5°和10.5°、周期为100 s的矩形波变化，倾侧角为固定值0°；

机动方式2：攻角为固定值8.5°，倾侧角按幅度分别为20°和-20°、周期为100 s的矩形波变化。

则飞行过程中，气动参数αVTC随时间的变化曲线如图10所示。从图10可看出，当目标按机动方式1飞行时，气动参数αV和αC随时间的变化曲线近似呈周期为100 s的矩形波，气动参数αT曲线呈线性；当目标按机动方式2飞行时，气动参数αV和αC随时间的变化曲线近似线性，气动参数αT曲线呈周期为100 s的矩形波。进而说明目标在飞行过程中，气动参数αV和αC与飞行器的攻角近似线性，气动参数αT与飞行器的倾侧角近似线性。

4 结论

(1)采用临近空间高超声速环境下气动力工程计算方法，以HTV-2的简化模型为例，对目标在滑翔段的受力特性和目标运动特性进行了仿真分析，验证了本文气动建模方法的可行性和有效性。

(2)为便于轨迹预测，给出了一组能够唯一确定目标的飞行状态，且在目标飞行过程中与目标的攻角和倾侧角近似线性的气动参数。下一步研究的重点和难点将是基于本文给定的气动参数进行目标跟踪和轨迹预测研究，为拦截高超声速飞行器提供先验信息，提高拦截可能性。

[1] Walker S H,Sherk J,Shell D,et al.The DARPA/AF falcon program: the hypersonic technology vehicle#2 (HTV-2) flight demonstration phase[C]//15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference,2008: AIAA-2008-2539.

[2] Norris J D,Lafferty J F,Smith M S,et al.Design and aerodynamic calibration of the new AEDC hypervelocity wind tunnel No.9 mach 8 nozzle[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit,2005: AIAA-2005-4278.

[3] Bolender M A.An overview on dynamics and controls modeling of hypersonic vehicles[C]//2009 American Control Conference.St.Louis: Hyatt Regency Riverfront,2009: 2507-2512.

[4] Zhang Y,Xian B,Diao C.Robust tracking control design for a flexible air-breathing hypersonic vehicle[J].Journal of Central South University,2014,21:130-139.

[5] Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rocket,2007,44(2):374-387.

[6] Adamov N P,Puzyrev L N,Kharitonov A M,et al.Damping characteristics of a reentry vehicle at hypersonic velocities[J].Journal of Applied Mechanics and Technical Physics,2014,55(5):870-876.

[7] Zhao J,Zhou R.Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J].Chinese Journal of Aeronautics,2013,24(6):1544-1553.

[8] 陆海波,刘伟强.迎风凹腔与逆向喷流组合热防护系统冷却效果研究[J].物理学报,2012,61(6):372-377.

[9] 李海宁,雷虎民,翟岱亮,等.面向跟踪的吸气式高超声速飞行器动力学建模[J].航空学报,2014,35(6):1651-1664.

[10] 陈小庆.高超声速滑翔飞行器机动技术研究[D].长沙:国防科学技术大学,2011.

[11] 杨皓云,贺正洪,钟明皓,等.高超声速飞行器侧向机动性能研究[J].科学技术与工程,2013,13(30): 9139-9143.

[12] 张栋,唐硕,李世珍.吸气式高超声速飞行器粘性力工程计算方法[J].固体火箭技术,2013,36(3): 291-295.

[13] Istratie V.Three-dimensional optimal skip entry with terminal maximum velocity[C]//New Orleans,LA: 1997:97-3483.

(编辑：吕耀辉)

Trajectory prediction oriented aerodynamic performances analysis of hypersonic vehicles

ZHAI Dai-liang1, LEI Hu-min1, LI Hai-ning2, ZHOU Jin1

(1.School of Air and Missile Defense,Air Force Engineering University,Xi'an 710051,China； 2.Troop No.95247 of PLA,Huizhou 516000,China)

In order to provide the prior knowledge for the trajectory prediction of hypersonic vehicle,trajectory prediction oriented aerodynamic performances analysis of hypersonic vehicles was researched.Firstly,the basic performances of the hypersonic reentry-glide vehicle were introduced,and the necessity of trajectory prediction for intercepting hypersonic vehicles was analyzed.Secondly,take HTV-2 as an example,its aerodynamic force and maneuvering performances were simulated through oblique-shock theory,piston theory and Prandtl-Meyer flow.The simulation results are identical to that in the references,which demonstrate the validity of the simulation method.What's more,in order to make the trajectory prediction possible,a new set of aerodynamic parameters was proposed based on the simulations of aerodynamic force above,which provides theoretical basis and reference for trajectory prediction of hypersonic vehicles.

hypersonic vehicle；trajectory prediction；aerodynamic force；glide；HTV-2

2015-11-24；

2016-03-21。

国家自然科学基金(61573374、61503408)；航空科学基金(20130196004、20140196004)。

翟岱亮(1987—)，男，博士，研究方向为目标跟踪、信息融合。E-mail：quietzdl@126.com

V211

A

1006-2793(2017)01-0115-06

10.7673/j.issn.1006-2793.2017.01.021