基于修正Arrhenius活化能方法的HTPB推进剂贮存寿命预估

杜永强，郑 坚，彭 威，张 晓，顾志旭

(军械工程学院，石家庄 050003)

基于修正Arrhenius活化能方法的HTPB推进剂贮存寿命预估

杜永强，郑 坚，彭 威，张 晓，顾志旭

(军械工程学院，石家庄 050003)

对HTPB推进剂高温加速寿命试验的老化起点进行了修正，并将Arrhenius方程中活化能与温度的函数关系修正为多项式形式。通过2种HTPB推进剂老化试验数据的回归结果得到修正活化能方法的老化模型，外推出25 ℃下的贮存寿命分别为12.8 a和11 a，与常温外推试验数据相符，且误差小于传统Arrhenius方法。

HTPB推进剂；活化能；修正Arrhenius方程；寿命预估

0 引言

复合固体推进剂是固体火箭发动机的核心，开展复合固体推进剂的贮存老化性能和寿命预估研究，对于火箭发动机的使用性能和安全可靠性具有重要意义[1]。目前，国内外常用研究方法是将高温加速寿命试验和Arrhenius方程结合，建立推进剂性能变化的老化模型，进而外推出常温下推进剂的使用寿命。传统的Arrhenius方程在处理数据时，将指前因子和表观活化能假设为常数，没有考虑其在温度下的变化，但通过理论推导和试验证明，这2个参数都和温度有关，不能作为常数处理。在对固体推进剂的寿命预估上，传统的Arrhenius方程也存在较大误差。因此，必须对该方程进行修正。

张昊等[2]从动力学理论分析入手，验证了活化能是老化温度的函数，活化能和老化温度存在线性依赖关系，并提出了预估推进剂寿命的四参数动力学模型。陈海建等[3]分析了传统Arrhenius方程的局限性，通过理论推导建立了基于Arrhenius方程的三参数公式，并和传统Arrhenius方程以及常温试验外推储存寿命进行了比较。结果表明，修正的Arrhenius方程预估精度更高。以上学者都对传统Arrhenius方程中的活化能进行了修正，有效减小了寿命预估的误差，但都没有考虑到推进剂在固化过程中伴随着老化，固化起点不等同于老化起点；另外，对于活化能的修正上，还可进一步缩小误差，使预估结果更符合实际贮存情况。

本文选择HTPB推进剂的老化模型为指数函数形式，对HTPB推进剂高温加速寿命试验的老化起点进行了修正。同时，结合传统Arrhenius方程中指前因子及活化能与温度的函数关系，修正该函数为多项式形式，通过试验数据拟合影响程度因子，分析不同温度函数关系对2种型号HTPB推进剂的影响。该方法可有效减小传统Arrhenius方程带来的误差，同时对不同型号的HTPB推进剂有良好的适应性。文中通过具体的老化试验数据，对该模型进行了验证。

1 分析和建模

1.1 老化起点的修正

本文选取的反应机理函数为国内外在对推进剂进行寿命预估时，通常采用的指数模型[4]：

(1)

式中P为推进剂老化后的力学性能参数；P0为初始性能值；K为性能变化速率常数;t为老化时间。

在固化过程中，老化反应也在同时进行。因此，固化终点并非老化起点。假设HTPB推进剂在温度T0下进行固化，加上固化前后的升降温时间，总共的固化时间为t0，其他温度下的对应时间用阿累尼乌斯导出式进行修正：

(2)

通过实测得到的推进剂活化能数据，代入式(1)可求得不同温度下的K值与固化温度T0下的K值之比。假设固化结束后式(1)中的(P/P0)为一定值，则可导出：

(3)

即可求得不同老化温度下的老化起点。

1.2 Arrhenius方程的修正

表观活化能Ea、指前因子A和反应机理函数P(k,t)是反应动力学方程中最重要的3个参数[5]。高温加速老化方法假设固体推进剂的老化反应速率K服从Arrhenius方程：

(4)

式中R为普适气体常数；T为热力学温度。

根据理论推导和老化试验可得出，活化能和指前因子均是温度的函数。因此，在进行试验数据处理时，不能将这2个参数假设为常数[6]。

通过加速老化试验表明，指前因子和温度的函数关系不同时，老化反应速率常数也存在区别。考虑到公式能更准确地预估试验老化模型，同时分析不同温度函数形式对反应速率常数的影响，选取指前因子和温度的函数关系为多项式形式：

(5)

所以，Arrhenius方程的形式修正为

(6)

(7)

式中Cm(m=0,1,2,3,4)，E均为待定系数。

从式(7)可看出，每个单独的反应速率常数在形式上为三参数Arrhenius方程。因此，本文推导的修正公式，可看作是不同形式温度函数的结合，但各自对反应速率的影响程度θm(m=0,1,2,3,4)，需要依据实际试验数据进行拟合。

对式(7)等式两边同时取对数，并对温度求导，整理得

(8)

对传统Arrhenius方程用同样的方式取对数求导，整理得

(9)

比较式(8)和式(9)可得，修正公式考虑到了温度对活化能的影响，结合不同温度下的影响程度，可有效地减小传统公式下假设活化能为常数带来的误差。

2 算例

2.1 老化起点的修正

本算例的试验部分数据来自文献[3]。对2种HTPB推进剂分别在50、60、70 ℃和35、50、65、80 ℃下进行高温加速老化试验，定期对推进剂的力学性能进行测试，并选取性能变化最显著的最大延伸率，作为性能评定参数[7]。

已知某HTPB推进剂在70 ℃下固化时间为3 d，加上前后升降温时间，总的固化时间为4 d，并且该型号的HTPB推进剂的活化能实测数据为21.338 kJ/mol，将数据代入到式(2)和式(3)中，可求得HTPB推进剂在70 ℃下固化4 d，相当于不同温度下的老化时间。修正的老化起点结果见表1。

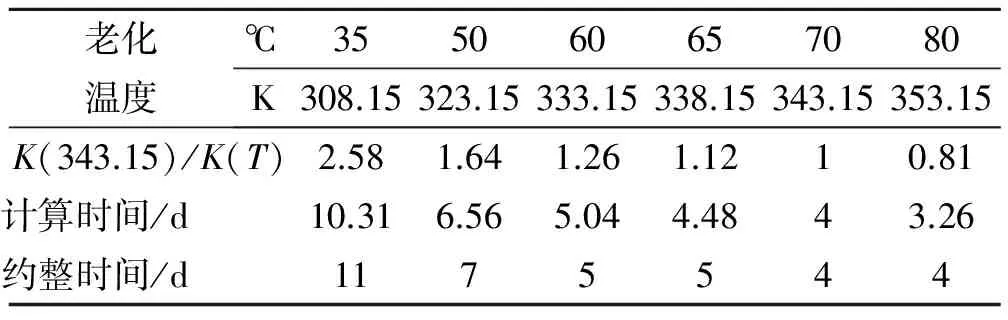
表1 修正后的老化起点

2种HTPB推进剂的最大延伸率随温度和老化时间的数据如图1所示。从图1可见，随着老化时间的增长，推进剂的最大延伸率呈下降趋势，且在相同的老化时间下，老化试验的温度越高，最大延伸率下降的越明显，这与高温下反应速率加快有关[8-9]。2#推进剂的老化速率明显快于1#推进剂，这与不同丁羟推进剂的配方有直接关系。由图1中数据拟合情况可见，试验数据符合本文选取的反应机理函数的指数模型。

2.2 模型参数的求解

本文求解采用分步回归的方法[10]。根据试验数据中推进剂力学性能P和贮存时间t的关系，借助最小二乘法对式(1)进行拟合，并对不同老化温度下的试验数据进行相关性分析，结果见表2。表中，n表示进行回归分析的数据对数，R表示相关性系数，R0.01表示显著性水平为0.01时的临界相关系数。

容易得出，在60 ℃和65 ℃条件下的老化反应模型与试验数据拟合的相关性最好。

对Km=CmTme(-E/RT),m=0,1,2,3,4分别进行回归分析，显然当m=0时，即为传统的Arrhenius方程，结果如表3所示。

拟合老化性能参数P与时间t的关系，得到影响程度因子θm(m=0,1,2,3,4)如表4所示。

1#HTPB推进剂以相关性最优的60 ℃下的回归数据拟合得到的老化模型为

(10)

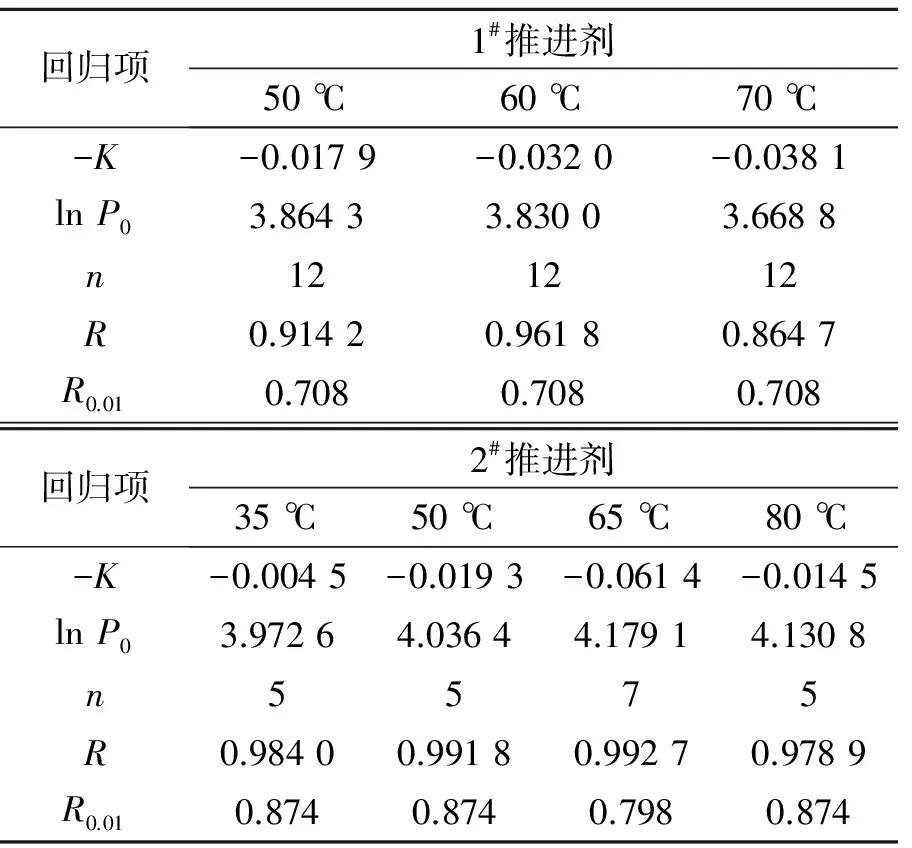
表2 1#推进剂数据处理结果

表3 反应速率函数各参数回归分析结果

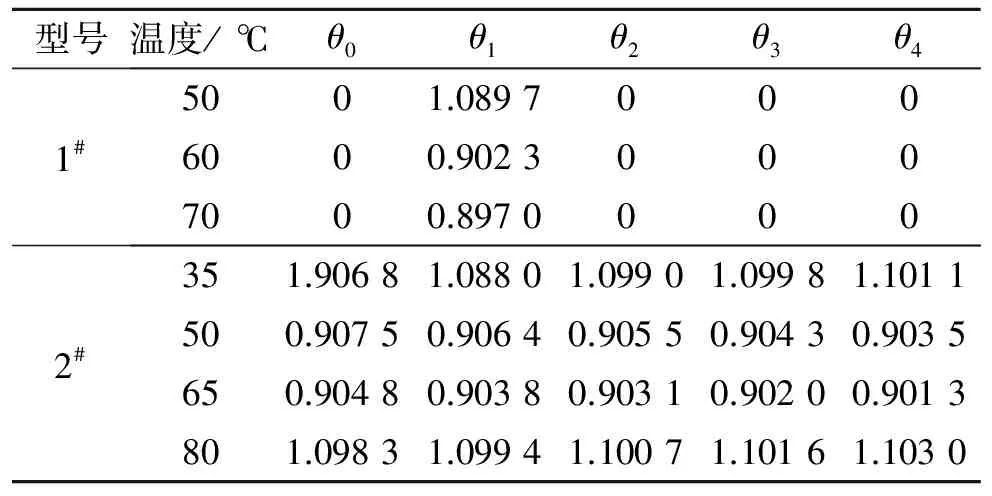
表4 影响程度因子

以推进剂最大延伸率下降至15%为失效判据[9]，预估推进剂在25 ℃贮存条件下的寿命，并与常温试验外推方法和传统Arrhenius方法进行比较，结果如表5所示。从表5可看出，活化能修正公式比传统的Arrhenius公式精确度更高。另外，活化能修正公式得到的老化寿命低于常温试验外推结果，从安全角度而言，该方法更符合实际要求。

表5 25 ℃下1#推进剂贮存寿命预估结果

2#HTPB推进剂以相关性最优的65 ℃下的回归数据拟合得到的老化模型为

(11)

用该模型预估HTPB推进剂的寿命，以最大延伸率下降到20%为失效标准，得到预估结果为11 a，以最大延伸率下降到15%为失效标准，得到预估结果为13.7 a，与实际贮存结果相符。

比较1#和2#HTPB推进剂的老化模型可看出，将传统Arrhenius方程活化能修正后，指前因子与温度的不同函数形式对推进剂的老化有不同程度的影响。1#推进剂中，该函数的影响主要呈现温度的一次形式，对2#推进剂该函数的影响呈现出多项式形式。该模型的处理方法可用于其他类型推进剂的研究中，具有一定的可扩展性。同时，修正后的Arrhenius方程有效地减小了把活化能假设为常数带来的误差，模型的寿命预估结果更精确。

本文提出的活化能修正公式是在文献[3]的三参数公式的基础上发展而来，假设活化能修正公式和HTPB推进剂的贮存状况能够有效吻合，则该公式对应的回归结果的相关系数以及与常温外推试验结果的相对误差要优于三参数公式。为了验证假设的正确性，将活化能修正公式和三参数公式的相关系数以及相对误差进行对比分析。考虑到推进剂在实际贮存时的温度不可能保持恒定，不同温度下推进剂的贮存寿命存在较大区别。因此，对这2种公式在不同温度条件下的推进剂贮存寿命预估结果进行了对比分析，结果如表6和表7所示。

表6 2种公式对比结果

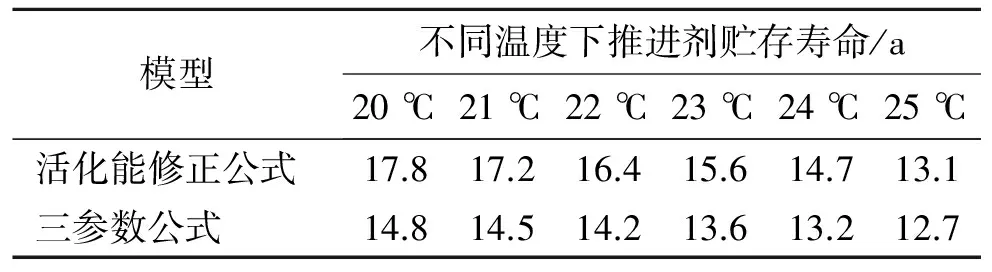
表7 不同温度下推进剂贮存寿命预估结果对比

综合表6和表7的对比分析结果可看出，活化能修正公式的相关系数和相对误差都要优于三参数公式。随着贮存温度的降低，推进剂的贮存寿命明显增加，说明低温贮存可有效提高推进剂的贮存寿命。25 ℃条件下活化能修正公式预估推进剂的贮存寿命为13.1 a，大于三参数公式的预估结果，但小于常温外推试验结果，活化能修正公式预估得到的寿命符合安全方面的规定，该结果可作为HTPB推进剂实际贮存的参考。

3 结论

(1)通过结合Arrhenius方程导出式和推进剂老化的指数模型，对不同老化温度下的推进剂老化起点进行了修正，确保老化试验数据更符合实际贮存状况。

(2)修正了传统Arrhenius方程中的活化能形式，提出了指前因子和温度的多项式关系，并结合2种HTPB推进剂的老化试验数据，以推进剂最大延伸率下降到20%为失效标准，外推出25 ℃下其贮存寿命分别为12.8 a和11 a，与常温试验外推数据相符，且误差小于传统Arrhenius方法。

(3)对不同型号的推进剂，活化能与温度的函数关系呈现不同的多项式形式，不同形式的温度函数的影响程度也各不相同，对该模型的处理方法可应用到其他类型的推进剂研究当中，本方法具有一定的可扩展性。

[1] 侯林法,杨仲雄,陈继周,等.复合固体推进剂[M].北京:宇航出版社,1994.

[2] 张昊,庞爱民,彭松.固体推进剂贮存寿命非破坏性评估方法(Ⅲ)——预测残留寿命延寿法[J].固体火箭技术,2006,29(4):279-282.

[3] 陈海建,滕克难,李波,等.基于修正Arrhenius方法的SRM药柱储存寿命预估[J].弹箭与制导学报,2011,31(4):232-235.

[4] Layton L.Chemical structural aging studies on HTPB propellant[R].AD-A010731,1975.

[5] 王春华.HTPB推进剂老化性能与贮存寿命预估的研究[D].长沙：国防科技大学,1998:45-53.

[6] 高大元,何碧,何松伟,等.Arrhenius方法的局限性讨论[J].含能材料,2006,14(2):132-135.

[7] GJB 770B—2005.火药试验方法[S].国军标,2005.

[8] 杨根,赵永俊,张炜,等.HTPB推进剂贮存期预估模型研究[J].固体火箭技术,2006,29(4):283-285.

[9] 李松年,刘勇,王罗新,等.HTPB推进剂储存老化性能试验研究[J].推进技术,2006,27(5):473-476.

[10] 傅惠民,杨立保,林逢春,等.固体推进剂贮存寿命整体预测方法[J].机械强度,2007,29(5):754-759.

(编辑：崔贤彬)

Storage life prediction of HTPB propellant based on modified Arrhenius activation energy method

DU Yong-qiang,ZHENG Jian,PENG Wei,ZHANG Xiao,GU Zhi-xu

(Ordnance Engineering College,Shi'jiazhuang 050003,China)

The aging starting point of the high temperature accelerated life test of HTPB propellant was modified,and the activation energy of the Arrhenius equation was modified to be a polynomial.The aging model of the modified activation energy method was obtained by the regression results of two kinds of HTPB propellant based on the aging test data,and the storage life of the new method is 12.8 a and 11 a respectively,which is consistent with the data from the temperature extrapolation test,and the error of which is less than the traditional Arrhenius method.

HTPB propellant;activation energy;modified Arrhenius model;storage life prediction

2015-12-08；

2016-03-23。

杜永强(1991—)，男，硕士生，研究方向为复合固体推进剂加速老化建模。E-mail：dyqangus@163.com

V512

A

1006-2793(2017)01-0081-04

10.7673/j.issn.1006-2793.2017.01.014