基于离散余弦变换的数字图像压缩算法实现

刘羽飞

基于离散余弦变换的数字图像压缩算法实现

刘羽飞

随着互联网通讯技术和数字媒体技术的快速发展，现代社会处于一种信息化时代，各种语音、文字、数字图像等大量的信息处于高速流通中。其中数字图像技术在各领域被广泛使用，对于数字图像的处理技术也得到迅速发展。但是一般数字图像都具有数据量大的特点，给图像传输、图像加密、图像存储等数字图像处理中的常见问题的解决增加了难度。数字图像这一特点是数字图像处理技术发展中必须克服的因素。

目前，数字图像压缩技术的研究与发展前景，受到更多学者专家的关注，越来越多的数字图像压缩技术被提出。数字图像的压缩也被称为数字图像编码，通过用少量的有效像素值将数字图像有损或者无损表示原来的数字图像技术。数字图像压缩技术的目的是要将原始数据量较大数字图像通过压缩技术后数字图像的数据量减少，但是压缩后的数字图像基本达到原始图像的效果，并包含主要信息，这样方便数字图像的传输、显示、交换等。目前，数字图像压缩处理技术领域常用的压缩方法有离散余弦变换理论、小波变换理论、图像压缩感知理论等。在国际上数字图像处理的JPEG的标准既通过使用离散余弦变换将获得的一幅数字图像各图像块的离散余弦变换DCT的系数，接下来通过对系数的量化，再对其进行熵编码得到压缩后的数字图像。图像在压缩后用于传输，因此图像在传输后需要解码，数字图像的解码就是压缩过程的逆变换。由于利用离散余弦变换对数字图像压缩具有较好的压缩效果，JPEG的图像压缩标准在各领域被广泛使用，目前在通讯及网络传输大部分的图像都是采用的JPEG的压缩标准[1-3]。数字图像小波变换压缩原理是将数字图像进行小波变换，在变换的过程中选择合适的小波基进行小波变换分解，进行小波变换后会产生小波系数矩阵，压缩过程就对变换后的小波系数矩阵进行量化。最后得到量化后的小波系数矩阵进行编码。在利用小波变换算法对数字图像压缩过程中最关键和最核心的是小波系数矩阵的量化过程，量化方式将直接导致和影响数字图像的压缩效果。数字图像的压缩感知理论是基于对数字图像进行直接随机观测，随机观测即随机采集数字图像中的随机数据信息，通过随机采集到的数字图像数据信息作为图像压缩的数据。在解码过程中对随机采集到压缩图像数据进行压缩感知信号的重组及重构还原出压缩前的数字图像信息。本文通过对数字图像进行离散余弦变换后进行频域压缩的方法，通过Matlab仿真实现与结果分析。通过仿真结果得出DCT变换在数字图像压缩应用中以下优点能进行快速压缩处理，压缩后图像质量较高，压缩过程中的计算效率高，有效地获得了更好的压缩效果[4]。

1 离散余弦变换

在数字图像处理中通常会将图像从空间域转换到频率域上进行分析处理。通过简单的积分变换就可以得到图像的空间频率成分，进而对图像在频域上进行处理。离散余弦变换也被看作为傅里叶变换的一种相关的频域变换方法，可以简称为DCT，其中离散余弦变换有具体的数学推导公式及过程，在不同的应用领域也分别会代表不同的物理意义[5-6]。

一维离散余弦变换：

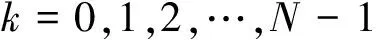
(1)

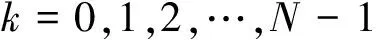
(2)

二维离散余弦变换如下：

(3)

其中u=0,1,2…M-1;v=0,1,2…N-1

(4)

(5)

其二维离散余弦变换的反变换如：

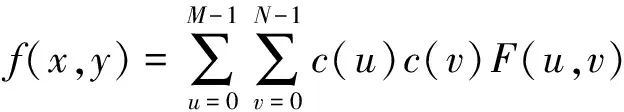
(6)

2 基于DCT的图像压缩算法

基于离散余弦变换DCT图像压缩方法的流程如图1所示，其算法步骤主要分为以下几步：第一步要将被压缩的图像进行分块处理，通常将图像分为8×8的图像子块。接下来第二步将对分好的每个子块进行离散余弦变换，变换后的图像低频部分都大部分集中在图像频谱图中的左上角处，而高频部分基本集中在频谱图的右下角区域中。由于数字图像中的主要数据信息都是低频的信息，主要存在低频部分，所以对应的离散余弦变换后的低频系数较大。高频部分包含的信息量小，对应的DCT系数比较小可以忽略。在数字图像压缩中，对图像的频谱图像的低频部分进行保留处理，及保存CDT变换后系数较大的部分，将高频系数较小的那部分舍弃，通常情况下人的眼睛对高频的信息不敏感，从而当高频部分被舍弃，人眼也很难察觉到有失真。在数字图像传输过程中，就是利用这个压缩特点，将图像变换后的高频信号系数舍去进行压缩数据的传输，当接收到图像压缩数据后需要还原图像，将压缩的图像数据进行离散余弦反变换恢复到原有的图像数据值。在这过程中图像会有一定的数据丢失，但是人眼还是无法直接看出。这就实现了数字图像压缩传输的目的。其次是进行DCT系数的量化，对图像进行量化将会导致图像的质量下降，图像经过DCT变换后，DCT系数的幅度可能较大，因此需要量化系数不为零的系数项减小其系数的幅度，有些高频系数可以量化为零，增加系数为零项的数目。在量化过程中，通常将低频部分的量化阈值系数设为较小的数值，最大限度地保留数字图像原有的主要数据信息。在高频部分设置系数阈值时，一般都将高频系数值设为零。一般情况下量化的阈值选定直接导致压缩的效果，即在图像的压缩比与图像质量之间的取舍，量化的阈值越大，图像的压缩比越高。通常情况下想要获得更好的图像压缩质量，则需要综合考虑设置合理的量化阈值对图像进行压缩处理。在量化编码过程中，其中DC为图像的直流分量，DC分量包含了图像频谱的主要部分，也包含了图像的主要信息，对其系数进行编码的系数一般取值较大。

图1 压缩过程

3 仿真结果与分析

在实验仿真中选取了一幅灰度级为0到255，图像大小为488×360像素的鲜花图像作为压缩处理的图像，对图像先进行二维离散余弦变化后的频谱图如图2所示，从实验仿真结果图可以明显看出二维离散余弦变化后图像左上角较亮，说明左上角数字较大，能量信息基本集中在左上角，通过舍弃右下角的高频数据将可以实现图像的压缩。

(a)

(b)

(a)

(b)

(c)

(d)

(e)

(f)

实验过程中采用保留不同个数的量化系数实现不同的压缩比进行压缩，实验结果如图3所示。为了直观地看清楚不同压缩比下的压缩图像效果，在图3中给出了六幅不同压缩比下的压缩图像，在图(a)(b)(c)三幅图像中分别保留了21,15,10个量化系数，在这三幅图像中还是可以清晰看到图像整体轮廓和细节，保存了较多原有的图像信息。图(d)(e)(f)三幅压缩图像分别保留了7,5,3个量化系数。从图中可以明显看到与前三幅压缩图像的压缩效果不同，后三幅图像出现了模糊的现象，保留了大致的轮廓，其中一些细节的东西显示不明显，图像出现了失真，图像的质量出现了下降。

通常用峰值信噪比(PSNR)来评价一幅图像压缩后和原图像相比质量的好坏， PSNR越高，压缩后失真越小。公式如下：

(7)

(8)

其中MNS表示均方差，MAX表示图像的灰度级。

其中图(a)(b)(c)(d)(e)(f)对应的PSNR值分别为81.054 8、76.383 5、70.235 8、50.487 2、42.698 1、36.584 2。虽然图5(f)压缩后的图像有些模糊，但PSNR值仍能达到36.5842，人眼在一定的误差范围内仍能接受。

通过仿真结果得知当图像要想获得较低的压缩比，就要保留较多的量化系数个数，这样通过DCT变换压缩后的图像质量较高。当图像量化系数个数保留较少时，获得较高的压缩比，但是数字图像的信息量会减少导致图像的质量下降。因此在实际的图像压缩处理中，则需要合理选择适合的压缩比对图像进行压缩处理以达到所要满足的图像质量要求。

4 总结

本文通过利用离散余弦变换DCT对数字图像表示从空间域变换到频域表示，根据离散余弦变换图像频谱分布的特点。通过舍弃部分数据，用较少的数据信息量来表示压缩后的图像，能较大地减少原始图像信息冗余的情况，从而实现了保留主要信息的同时较好地压缩了数字图像的数据量。使用MATLAB实验仿真，对数字图像进行了不同程度的压缩，给出了保留不同量化个数下图像的压缩效果图，对压缩图像进行了分析。通过实验仿真结果表明离散余弦变换DCT应用在数字图像压缩中取得了较好的效果，表明该方法有很高的可行性，其操作简单，压缩处理计算快，压缩后的图像质量较高，能有效减少图像的数据量，便于图像的保存及传输。

[1] 刘雅莉.二维DCT 变换在JPEG图像压缩中的应用及其MATLAB实现[J]. 理论与算法, 2014(5): 33-35.

[2] 武瑛.DCT变换在图像压缩中的应用[J]. 计算机与现代化, 2013(4): 103-106.

[3] 陈一虎.基于离散余弦变换的图像压缩研究[J]. 现代电子技术, 2011, 34(21): 86-88.

[4] 陈波, 王红霞, 成礼智. 图像压缩中的快速方向离散余弦变换[J]. 软件学报, 2011, 22(4): 826-832．

[5] 姚军财.一种基于DFT 的数字图像压缩算法[J]. 陕西理工学院学报( 自然科学版), 2012, 28(3): 22-25.

[6] 王新年, 张涛. 数字图像压缩技术实用教程[M]. 北京: 机械工业出版社, 2009.

责任编辑 陈桂梅

(韶关学院 物理与机电工程学院，广东 韶关 512005)

随着互联网技术及通讯技术的快速发展，数字图像被广泛使用。对数字图像的压缩技术是数字图像处理技术中的关键技术之一。本文介绍了一种基于离散余弦变换(DCT)频域变换方法，使用该方法对数字图像进行图像数据的压缩。该方法用MATLAB仿真软件对实验测试的数字图像进行压缩，对比不同压缩比下的压缩图像进行分析，通过实验仿真结果得出离散余弦变换应用在数字图像压缩中有良好的效果。该方法具有操作简单，处理速度快，易于操作，压缩图像质量高等优点。

图像压缩； 离散余弦变换

Digital Image Compression Based on Discrete Cosine Transformative Algorithm

LIUYufei

(School of Physics and Electrical and Mechanical Services, Shaoguan University,Shaoguan 512005, China)

With the rapid development of Tnternet and communication technology, digital image is widely used. The digital image compression is one of the key technologies of digital image processing techniques. This paper introduces a method in digital image compression, which based on using discrete cosine transform (DCT) frequency domain. The processes of compare and analysis the compressed images are done by the MATLAB simulation software in different compression ratio. The result shows the discrete cosine transform gains great effect than others. The advantages of the DCT method are easy operation, fast processing and high quality compression image.

image compression; discrete cosine transform

10.13750/j.cnki.issn.1671-7880.2017.01.012

2016-09-15

刘羽飞(1989— )，男，广东韶关人，硕士，研究方向：自动化装置及检测技术，数字图像处理。

TN 911.73

A

1671-7880(2017)01-0043-04