基于非均匀性和分形维数的黄土优先流特征定量分析

潘网生，许玉凤，卢玉东，高礼安，姚 兴



基于非均匀性和分形维数的黄土优先流特征定量分析

潘网生1,2，许玉凤1，卢玉东2，高礼安1，姚 兴1

（1. 黔南民族师范学院旅游与资源环境学院，都匀 558000；2. 长安大学环境科学与工程学院，西安 710054）

该文以陕西泾阳南塬边坡黄土为例开展示踪剂试验，通过改进的优先流入渗深度和入渗量非均匀性系数，研究黄土优先流的入渗量、入渗深度、含水率、孔隙率、分形等参数的相互关系及其内在规律。结果表明：1）入渗量越大，优先流入渗深度的非均匀性越明显；2）初始含水率越高，优先流发育程度越低，而湿润锋迹线的分形维数越小；3）黄土孔隙率越大，优先流入渗深度的非均匀性越明显，且入渗深度值波动范围也相对较大；4）同一类型的黄土，其试验尺度大小对湿润锋迹线的分形维数没有明显影响；5）在0.5倍黄土优先流最大入渗深度范围内，分形特征值越大，优先流非均匀程度越强，优先流越发育；6）在没有明显优先流渗流通道情况下，90 mm地表灌溉水量，其最大入渗深度不超过120 cm。考虑正常蒸发和没有裂缝的前提下，地表灌溉水并不容易直接导致地下水位上升。由此推断，优先流在地表水向地下水转换过程中发挥着重要作用。同时，优先流对黄土滑坡的影响不容忽视。研究可为深入揭示黄土优先流渗流特征与黄土优先流滑坡的内在联系提供依据。

入渗；土壤；分形维数；黄土；优先流；示踪试验；渗流特性

0 引 言

优先流是描述土壤在多种环境条件下发生非平衡渗流过程的专业术语[1]。优先流研究包括指流（finger flow）、大孔隙流（macropore flow）和漏斗流（funnel f1ow）3种类型。国外开展优先流研究较早，1973年Petrus提出了优先流概念雏形[2]。自1989年Monte Verita学术会议后，优先流的普遍存在及其研究意义引起了学术界的广泛关注，大量的田间和室内试验研究由此展开[3]，并取得了丰硕的研究成果。近年来，国外学者基于示踪剂[4-7]、模拟试验[8]及时域反射仪（time domain reflectometry，TDR）等技术[9]研究优先流的渗流路径、分形、多样、不稳定、周期性及时间差异性等特征[10-12]。国内学者针对不同土壤类型开展土壤含水量及优先流渗流特征研究，主要包括非饱和土特性[13]、原状黄土土柱[14]、山地和平原地区甚至绿洲地区的耕地土壤[15-17]、森林土壤[18]、黑垆土及渭河砂土[19]等，主要研究手段是染色示踪法[20-24]。

目前，优先流研究主要涉及农业、林业、生态、环境污染等领域，关于黄土优先流的研究较少，黄土优先流与黄土地质灾害关系的研究则更少。在内外营力作用下，黄土内部形成了不同规模、不同尺度、不同时期序列的裂隙、节理和孔洞，其种类、结构形态及其连通性直接决定着黄土渗透性质，造成降雨或灌溉入渗的显著差异。这种差异使得部分雨水或灌溉水汇聚于黄土优势渗流通道，迅速入渗至黄土斜坡深部，控制了潜在滑动面的形成、扩展和贯通，进而导致黄土斜坡不稳定，易诱发优先流型黄土滑坡。但由于黄土优先流入渗途径较为复杂，黄土优先流控滑机理研究相对薄弱，优先流主导的滑坡机理尚未引起学术界的足够关注和重视，致使一些事实上的优先流型黄土滑坡没有得到科学合理的解释。因此，在此背景下开展黄土优先流渗流特征研究有着重要的理论和现实意义。

宏观视角的黄土斜坡优先流渗流特征研究一般通过数值模拟进行分析，难以通过现场试验手段获得全面的第一手资料，而微细观视角的黄土优先流渗流特征试验研究则可以弥补前者不足，为宏观黄土斜坡优先流渗流特征及规律研究提供佐证。因此，为了剖析黄土优先流的入渗量、入渗深度、含水率、孔隙率、分形等参数的相互关系及其内在规律，揭示黄土优先流渗流特征与黄土优先流滑坡的内在联系，本文以泾阳南塬黄土体为研究对象，开展微细观尺度的优先流渗流特征试验研究，以完善多尺度视角下黄土优先流渗流理论体系，为宏观黄土斜坡优先流渗流数值模拟、优势滑动面形成机理及优势滑动面搜索方法研究提供理论依据，对黄土滑坡灾害治理也具有重要的理论意义和应用价值。

1 材料与方法

1.1 试验地概况

试验地选择在泾阳县南塬东风村黄土边坡弃耕地，其地理位置为108°50¢48²E，34°29¢25²N。试验区北侧为泾河南岸陡坡，南侧为坟地和砖厂（图1）。根据试验区黄土孔隙率相对差异，将试验区分为试验Ⅰ区和试验Ⅱ区，每个试验区黄土剖面质地相对均匀，没有明显的大孔隙和裂隙结构。试验Ⅰ区和试验Ⅱ区的土体物理性质见表1。表1中数据除残余含水率依据测定时间段空气湿度做经验判定外，其他均通过室内试验获取，其中孔隙率由取自该试验坑土块的Quanta 200型扫描电镜（荷兰FEI有限公司）图像分析获取，饱和渗透系数由TST-55型渗透仪（河北省虹宇仪器设备有限公司）测得。

图1 试验场地概况

表1 不同试验区黄土的物理性质参数

土水特征曲线由TEN60型土壤张力计（浙江托普仪器有限公司）对黄土土柱进行增湿测定，并由van- Genchten模型拟合（饱和渗透系数取平均值）。van- Genchten模型公式[25]如下：

式中为含水率；θ为饱和含水率；θ为残余含水率；和为拟合形态参数；1-1/；为土壤基质吸力，kPa。渗透性函数曲线见图2。试验区I的和分别为27.73 kPa和1.82；试验区II的和分别为22.36 kPa和1.64。

图2 2个试验区黄土渗透性函数曲线

Fig.2 Permeability function curve of loess in 2 regions

1.2 示踪试验法

本文采用示踪剂技术对优先流渗流特征进行现场试验，试验于2014年10月进行，夜晚最低气温12 ℃，白天最高气温26 ℃。示踪试剂为碘化钾-淀粉，其基本原理如下：碘化钾中的碘离子在硝酸铁作用下被氧化成碘分子，淀粉吸附碘分子过程中发生显色反应，利用该显色对优先流路径进行追踪与描述。示踪剂的配制[26]：碘化钾溶液质量浓度为20 g/L，淀粉溶液质量浓度为50 g/L，硝酸铁溶液质量浓度为20 g/L。将配制好的淀粉溶液与硝酸铁溶液混合摇匀。

试验设计见表2，在试验Ⅰ和Ⅱ区分别开挖4个试验坑。所有试验坑平面为边长相等的矩形（×），试验坑之间距离＞3 m。根据双环渗透原理，用铲刀开挖2个同心环状正方形试验坑，1～7号试验坑的内坑尺寸50 cm´50 cm，同心环状外坑宽10 cm，内坑与外坑之间的土埂宽10 cm，内外坑深度均为10 cm。8号试验坑的内坑尺寸100 cm´100 cm，同心环状外坑宽10 cm，内坑与外坑之间的土埂宽10 cm，内外坑深度均为10 cm。

表2 试验设计

试验前将每个试验场所50 cm厚度的地表土铲除并开挖剖面，在深度分别为0～20、＞20～40、＞40～60、＞60～80和＞80～100 cm处，按水平间隔20 cm用环刀（100 cm3）取未扰动土样，测定土壤基本物理性质。为了增大试验土体初始含水率，试验前10 d单独对4#试验坑以40 mm入渗水量进行预先增湿处理。

先后向开挖好的8个试验坑的内坑注入配制好的碘化钾溶液，外坑注入同样高度的清水。待碘化钾溶液完全入渗后，用防水隔热材料将试验坑覆盖。12 h后开挖垂直剖面，剖面间距为5 cm。剖面开挖形成后，向剖面均匀喷洒配制好且充分摇匀的淀粉和硝酸铁混合溶液。显色完成后，用奥林巴斯SZ-15高清照相拍摄各剖面的染色图像。拍照之后，对垂直剖面的染色区域和非染色区域分别取样测试土壤含水率，取样前必须铲掉表层2 cm厚的土层，以保证含水率测试数据准确。染色区域采样剖面间隔10 cm，未染色区域采样剖面间隔20 cm。

1.3 图像预处理方法

显色完成后采用高清相机拍摄染色图像，并采用MATLAB软件作二值化处理（图3），分别得到各剖面优先流渗流特征图。需要说明的是，根据试验前对研究区黄土酸碱度测定，pH值范围为6.7～6.9，呈弱酸性。由于该弱酸性土壤环境不利于碘化钾中碘的析出，因此在一定程度上影响到本试验染色效果。

图3 图像二值化过程

1.4 优先流渗流特征参数确定

1.4.1 非均匀性分析法确定入渗深度和入渗量

1）入渗深度的非均匀性分析

盛丰[27]在用示踪剂试验研究优先流时，引入实际入渗深度替代最大入渗深度描述优先流非均匀特征。笔者认为，该概念的引入可能导致不能真实、完整描述优先流非均匀特征的问题。因为相邻剖面最大入渗深度往往具有相似性，侧向入渗的发育，常导致相邻剖面染色效果不一致，这也正是优先流本质特征表现。由于不能切开所有剖面获得试验数据，故不能明确判断最大入渗深度上方未被染色的具体原因。因此，难以确定实际入渗深度值。本文认为采用最大入渗深度描述优先流非均匀特征更符合实际。本文定义优先流入渗深度非均匀系数为

式中C为优先流入渗深度非均匀系数；max(x,y)为(x, y)位置处被染色的最大入渗深度；为不同(x, y)位置处被染色最大入渗深度的平均值；为试验坑剖面平行方向（或剖面垂直方向）的像素点总数目。

2）入渗量的非均匀性分析

Kamra等[28]研究认为，在优先流存在条件下，溶质运移主要通过水动力弥散作用、二域作用以及优先流作用共同完成。郭会荣等[29]在基于室内土柱穿透试验的优先流定量评价研究中，将溶质运移引起的穿透曲线延展量定义为由水力弥散延展量、二域溶质交换延展量及优先流穿透曲线延展量3部分构成，并采用优先流综合评价指标定量描述优先流程度，取得了良好的定量评价效果。因为二域溶质交换量很小，交换机理研究目前尚不明确，且二域溶质交换在本质上并不影响优先流形态特征，故本文忽略二域溶质交换延展量的影响，以E表征优先入渗量的非均匀性，该值越大，表明优先入渗量越大，优先流发育程度越明显。E数学表达式如下：

式中0、θ分别为试验前、后土体体积含水量，cm3/cm3；min为剖面最小入渗深度，cm；为试验注水深度，cm。

为进一步研究黄土优先流渗流特征，本文采用英国统计学家卡尔·皮尔逊提出的简单相关系数法[30]。通过剖面平行方向、剖面垂直方向入渗深度的互相关函数关系揭示入渗深度的分布规律。该方法用以表征优先流入渗深度沿2个相互垂直的不同方向分布的相关程度，其中一个方向的计算结果用以比较优先流各剖面内部入渗深度的非均匀程度，而另一方向的计算结果用以比较优先流各剖面之间入渗深度的非均匀程度。相关性系数大于0，且变化幅度小于50%，表明剖面内部及剖面之间优先流入渗深度的相关性较强，即表征优先流入渗深度在空间分布上相对均匀。反之，当某一剖面内部或剖面之间相关性系数有正数变负数或由负数变正数，且变化幅度较大，则表明优先流入渗深度在空间分布上极不均匀。

1.4.2 分形维数及分形特征分析法

1）分形维数计算方法

野外试验中数码影像所记录的被示踪剂染色的优先流湿润锋迹线，具有明显的不规则、分裂、无序又支离破碎的复杂结构，即具有分形特征。近年来，分形维数已经成为刻画优先流的重要定量化指标。本文研究采用像素点覆盖法研究分形维数，该方法的核心思想是采用正方形的像素格网覆盖优先流湿润锋迹线，盒子的边长记为δ，所覆盖住优先流湿润锋迹线的盒子数目记为(δ)[31]。设为分形维数，其数学表达式为

= 1时，表明湿润锋迹线为直线，此时即为均匀渗流状态，不存在优先流；> 1时，表明湿润锋迹线为不规则曲线，此时存在优先流，且分形维数越大，表明优先流发育程度越强，反之亦然。

2）基于活动流场模型的分形特征参数计算方法

活动流场模型理论认为，土壤中的水分运移仍然遵循连续性模型的一般规律，可以用Darcy定律和Richards方程描述，且活动流场内土壤含水率与基质势满足Van Genuchten函数关系。盛丰给出二维坐标下活动流场模型的水流控制方程，并基于分形的活动流场模型理论，将渗流场划分活动流场和不活动流场，认为活动流场具有分形特征。活动流场在整个渗流场中所占的比例与活动流场模型分形特征参数之间存在某种函数关系[27]：

式中S为活动流场区域的平均水饱和度。

此外，活动流场模型分形特征参数的物理意义由下式表示[27]：

式中0为活动流场分形维数；0为欧拉维数。是描述优先流非均匀程度的指标，越大，表示非均匀程度越强，=0表示当前渗流为均匀渗流状态。

2 结果与分析

2.1 优先流渗流影像特征

以1#、2#、3#和8#试验为例，图4表明试验结束后12 h开挖断面典型剖面渗流特征影像二值化结果。由图4可知，黄土渗流过程确实存在优先流渗流现象，且优先流渗流分叉出现在入渗湿润锋部位，从形态特征看无一定规律可循，但其入渗深度与入渗量存在明显相关性，即入渗量越大，入渗深度亦越大。

染色面积比例是直观、定量描述优先流在垂直剖面运动轨迹的一种方法，通过绘制垂直方向的不同剖面即可获得优先流三维空间分布特征。结果表明（图5），不同试验染色面积比例均随优先流入渗深度增大而减小，说明入渗过程非均衡进行，存在明显的优先流渗流现象。

注：以试验坑一角为原点，建立三维坐标，x为离试验坑一角的水平距离，y垂直于x，下同。

图5 不同试验染色面积比例分布

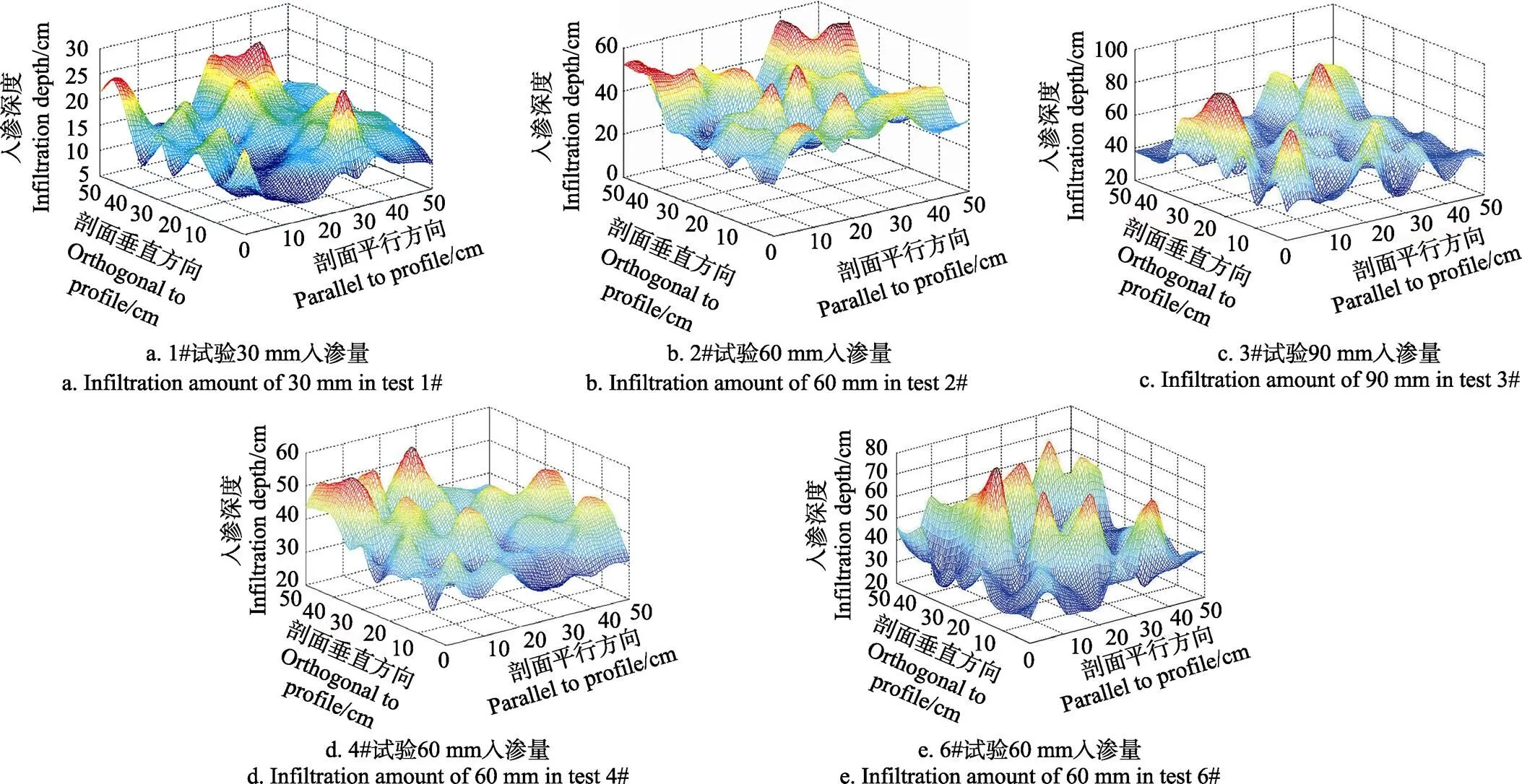
图6 不同入渗条件下水流入渗深度的空间分布

2.2 入渗深度空间分布

为反映入渗深度的空间分布特征，将每个试验区地表离散成5 cm×5 cm的正方形网格，由此每个试验得到100个正方形网格，应用MATLAB软件绘制1#、2#、3#、6#试验入渗深度分布三维图（图6）。结果表明，黄土优先流的入渗深度在空间上存在极大差异。

以5个试验为例表明优先流入渗深度非均匀系数变化，如图7所示。比较图7a～c可知，1#试验C在剖面平行方向和剖面垂直方向变化幅度均处于0.1～0.25之间，且在近距离区间，2个方向的C值呈现为大体一致的变化趋势，但随着距离增大，C值呈现异化。2#试验剖面平行方向C变化幅度在0.2～0.25之间，保持相对稳定，而剖面垂直方向C波动较大，变化幅度在0.05～0.3之间。3#试验剖面平行方向和剖面垂直方向的C变化幅度在0.05～0.35之间，且2个方向的C值呈现为大体一致的变化趋势。由上述数据分析可知，相同类型黄土、相同初始含水率条件下，随着入渗量增大，C变化幅度呈增大趋势，但剖面平行方向和剖面垂直方向的C的异化程度呈逐步减小趋势，表明渗流垂向不均匀性大于水平的不均匀性，也表明入渗量多少对入渗深度的非均匀特征具有明显影响。

图7 各试验入渗深度的非均匀系数Cμ

由图7d可知，4#试验C值变化幅度在0.05～0.18之间，比较图7b可知，在相同入渗量条件下，初始含水率越大，C变化幅度越小。此外，根据图7d统计结果，4#试验的入渗最小深度和入渗平均深度均大于2#试验，即表明初始含水率对优先流入渗深度的非均匀特征具有明显影响，且初始含水率越大，优先流平均入渗深度越大，优先流入渗深度的不均匀特征越不明显。进而可以推断，黄土初始含水率越大，优先流通过的速度越快。

由图7e可知，6#试验剖面平行方向和剖面垂直方向的C值幅度在0.1～0.3之间，且2个方向的C表现为大体一致的变化趋势，表明水平方向的渗流较为均匀。与图7b比较可知，相同入渗量条件下，大孔隙率黄土C值大于小孔隙率黄土C值，且波动范围也相对较大，表明黄土孔隙率大小也是影响黄土优先流入渗深度非均匀性的重要因素。

根据皮尔逊简单相关系数法计算结果（表3），随着入渗量增大，黄土优先流入渗深度的相关系数变化幅度也在增大，即表征优先流入渗深度的非均匀性越来越明显；通过比较2#试验和4#试验计算结果得出：相同入渗量条件下，初始含水率对优先流入渗深度的相关系数有着明显影响，初始含水率越大，黄土优先流入渗深度在不同方向上的相关系数越大，即表征优先流入渗深度的非均匀性越不明显；通过比较2#试验和6#试验剖面垂直方向计算结果得出：相同入渗量的条件下，黄土孔隙率大小对优先流入渗深度的相关性系数影响比较明显，孔隙率越大，不同方向入渗深度的相关性系数变化幅度越大，即表征优先流入渗深度的非均匀性越明显。

表3 各试验入渗深度的相关系数

此外，由表3可知，优先流入渗深度相关系数在剖面平行方向和剖面垂直方向上总体波动较大，产生这种现象的可能原因是黄土孔隙通道形态特征和空间分布的无规律性所造成，这种情况也说明研究区黄土优先流入渗深度非均匀程度较明显，优先流特征也较明显。

2.3 入渗量变化特征

以5个试验为例表明优先流入渗量非均匀系数E变化特征（表4）。1#试验、2#试验、3#试验的E变化范围基本一致，即0.3～0.55之间，由此可以判断同一类型的土质、相同初始含水率条件下，入渗量非均匀程度并没有本质区别。

表4 各试验入渗量的非均匀系数

4#试验入渗量非均匀系数E变化范围在0.2~0.37之间，明显小于2#试验。表明初始含水率对入渗量非均匀程度具有明显影响，初始含水率越大，优先入渗量越小，优先流发育程度越不明显，反之亦然。但结合统计资料，初始含水率越大，平均入渗深度越大，进而可以推断，平均入渗量也越大。6#试验E变化范围在0.2～0.44之间，其变化幅度大于2#试验（0.33～0.53）。由此表明，黄土孔隙率对优先入渗量存在明显影响，孔隙率越大，入渗量的非均匀性特征越明显，优先流发育程度越明显。

试验前后分别通过采用烘干法测定土壤含水率，再由干容重计算转化为体积含水量（图8）。试验前后含水量分布基本呈现“V”型，初始含水量随深度增大逐步增大，并在某一深度保持相对稳定，试验后的土壤含水量随深度增加而逐步减小，并在某一深度保持相对稳定，即达到该深度部位的初始含水量。由图8b可知，2#试验与4#试验设计注水量相同，但由于4#试验在10 d前以40 mm入渗水量进行预先增湿，故4#试验初始含水量较大，“V”型深浅与初始含水量及入渗量有着密切关系，初始含水量越大，“V”型越浅，反之亦然。入渗量越大，“V”型越深，反之亦然。

图8 试验前后土壤体积含水量

2.4 分形维数及分形特征分析

利用MATLAB编制程序实现对图像分形维数自动计算，通过对koch曲线、sierpinski三角形验证，表明该程序计算结果的精度较高（相对误差＜5%），可以用来计算优先流湿润锋迹线分形维数。计算结果如表5所示。

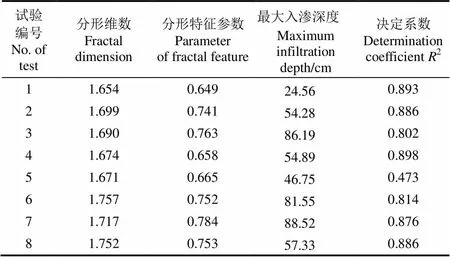
表5 不同试验优先流湿润锋迹线分形参数

表5表明，1#、2#、3#试验湿润锋迹线分形维数先增大后减小，比较5#、6#、7#试验湿润锋迹线的分形维数，同样是先增大后减小，表明孔隙率大致相同的一类黄土的优先流发育程度与入渗量存在一定的关系，即存在一个最佳入渗量使得该类黄土优先流发育最为明显。这与盛丰[27]研究结论一致。此外，比较2#和4#试验计算结果，含水率对优先流发育程度存在一定的影响，初始含水率较大的黄土，湿润锋迹线的分形维数则较小。比较6#和8#试验计算结果，分形维数没有明显变化，表明同一类型的黄土，其试验尺度的大小对湿润锋迹线的分形维数没有明显影响。

根据式（5）～（7），分别对1#～8#试验在0～0.5max（最大入渗深度）深度范围的染色面积比例及含水率数据做拟合分析。拟合结果表明，0～0.5max深度范围的具有较高的决定系数2。而对0～0.75max深度范围的拟合精度较低，2变化范围在0.673～0.698之间，对0～max深度范围的拟合精度更低，2变化范围在0.436～0.507之间。由此说明，分形特征参数可以在一定深度范围内定量描述黄土优先流渗流非均匀特征，但不能完整地定量描述优先流非均匀特征，因此在应用方面存在一定的局限性[27]。此外，该方法遇到大孔隙流时，拟合精度极低（5#试验）。比较6#、7#试验测定的值（表5），较大孔隙率的黄土分形特征值随入渗量增大变化不明显，该结论与盛丰[25]的研究结论基本一致。通过比较1#、2#、3#试验实际测定的值，表明较大孔隙率的黄土分形特征值随着入渗量增大呈现增大趋势，与6#、7#所得出的结论基本相符。

3 讨 论

优先流研究实践表明，对其本质规律的揭示、数学模型的构建、推导、改进及验证，都离不开对优先流现象的正确解析。虽然本文采用的示踪剂试验方法较为传统，但仍是目前国内外直观描述优先流现象特征和内在规律的重要手段之一。

细观黄土体优先流渗流特征是宏观黄土斜坡优先流渗流特征的缩影，研究细观黄土体渗流特征及其内在规律是认识宏观黄土斜坡优先流渗流特征、规律及其致灾机理的必由之路。本研究试验证明，细观黄土体优先流渗流具有明显的分形特征。根据分形自相似性原理，本研究成果可以为宏观黄土斜坡优先流渗流特征、规律及其致灾机理研究提供基础数据和理论依据。

泾阳南塬塬边多是高陡斜坡，裂缝发育，且主要集中在滑坡相对活跃地段，如太平镇寨头村和高庄镇东风村附近，主要是由于农业不合理灌溉导致地下水位上升所致[32]。根据本文3#试验研究结果，在没有明显优先流渗流通道情况下，90 mm地表灌溉水量，其最大入渗深度不超过120 cm。即在考虑正常蒸发、没有裂缝的前提下，地表灌溉水并不容易直接导致地下水位上升。泾阳南塬滑坡之所以发生，与塬边裂缝发挥优先流渗流作用不无关系。长期不合理的农业灌溉，使得灌溉优先流借助裂缝优势通道快速到达斜坡体深部，直接导致地下水位持续上升，进而改变坡脚土体抗剪强度，引发黄土斜坡滑坡。因此，泾阳南塬滑坡本质上应属于黄土优先流滑坡。

研究区黄土呈弱酸性，弱酸性环境对以碘化钾作为示踪剂的试验数据结果产生一定的偏差，但对描述优先流现象及其渗流规律并无本质影响。此外，当存在大孔隙流时，活动流场模型即失去应用价值。因此，进一步开展针对大孔隙流的理论模型研究工作是今后值得关注的研究方向。

4 结 论

1）入渗量多少对入渗深度的非均匀特征具有明显影响；初始含水率越大，黄土优先流入渗深度在不同方向上的相关系数越大，优先流入渗深度的非均匀性越不明显；黄土孔隙率越大，优先流入渗深度的非均匀性越明显，入渗量系数的非均匀性特征越明显。

2）初始含水率较大的黄土，湿润锋迹线的分形维数则较小；同一类型的黄土，其试验尺度的大小对湿润锋迹线的分形维数没有明显影响。

3）在0.5倍的黄土优先流最大入渗深度范围内描述活动流场比例具有一定的实践指导意义，湿润锋迹线的分形特征值越大，优先流非均匀程度越强，优先流越发育。

4）在没有明显优先流渗流通道情况下，90 mm地表灌溉水量，其最大入渗深度不超过120 cm。即考虑正常蒸发、没有裂缝前提下，地表灌溉水并不容易直接导致地下水位上升。

[1] Flury M, Flühler H, Jury W A, et al. Susceptibility of soils to preferential flow of water: A field study[J]. Water Resources Research, 1994, 30(7): 1945－1954.

[2] Petrus A C R. Refraction of a fluid at an interface between two anisotropic porous media[J]. Zeitschrift für angewandte Mathematik and Physik ZAMP, 1973, 24(1): 43－53.

[3] Clothier B E, Green S R, Deurer M. Preferential flow and transport in soil: Progress and prognosis[J]. European Journal of Soil Science, 2007, 59(1): 2－13．

[4] Gumm L P, Bense V F, Dennis P F, et al. Dissolved noble gases and stable isotopes as tracers of preferential fluid flow along faults in the Lower Rhine Embayment, Germany[J]. Hydrogeology Journal, 2016, 24(1): 99－108.

[5] Adrian A H, Steve W L, Peter A T, et al. The hydrological effects of lateral preferential flow paths in a glaciated watershed in the Northeastern USA[J]. Vadose Zone Journal, 2010, 9(2): 397－414.

[6] Horst H G, Peter G, John N. Preferential and unstable flow: from the pore to the catchment scale[J]. Vadose Zone Journal, 2010, 9(2): 207－212.

[7] Kung K J S, Hanke M, Helling C S, et al. Quantifying pore- size spectrum of macropore-type preferential pathways[J].Soil Science Society of America Journal, 2005, 69(4): 1196－1208.

[8] Annalisa G, Vincenzo S. Effects of preferential flow pathways on groundwater resources rainfall supply[J]. Engineering Geology for Society and Territory, 2015, 3: 257－260.

[9] Hasan M. Using TDR and modeling tools to investigate effects of interactive factors on preferential flow and transport in field sandy clay soil[J]. Environmental Earth Sciences, 2014, 71(4): 1821－1838.

[10] Marcus H, Richard D, William C, et al. Hydropedology and preferential flow in the Tasmanian texture-contrast soils[J]. Vadose Zone Journal, 2013, 12(4): 1－14.

[11] Chris B G, Henry S L. Controls and frequency of preferential

flow occurrence: A 175-event analysis[J]. Vadose Zone Journal, 2011, 10(3): 816－831.

[12] Martin H, Peggy A O, Javier G G, et al. Arsenic, copper, and zinc leaching through preferential flow in mining-impacted soils[J]. Soil Science Society of America Journal, 2012, 76(2): 449－462.

[13] 张丽华，王成武. 非饱和土壤优先流运动特性的染色示踪研究[J]. 节水灌溉，2010(5)：35－39. Zhang Lihua, Wang Chenwu. Using dye tracer to characterize preferential flow movement on soil surface[J]. Water-saving Irrigation, 2010(5): 35－39. (in Chinese with English Abstract)

[14] 徐学选，陈天林. 黄土柱入渗的优先流实验研究[J]. 水土保持学报，2010，24(4)：82－85. Xu Xuexuan, Chen Tianlin. Experimental study on infiltration of Loess column though preferential flow[J]. Journal of Soil and Water Conservation, 2010, 24(4): 82－85. (in Chinese with English Abstract)

[15] 蒋小金，王恩姮，陈祥伟，等. 典型黑土耕地土壤优先流环绕特征[J]. 应用生态学报，2010，21(12)：3127－3132.Jiang Xiaojin, Wang Enheng, Chen Xiangwei, et al. Surrounding characteristics of preferential flow in cultivated typical black soils of Northeast China[J]. Chinese Journal of Applied Ecology, 2010, 21(12): 3127－3132. (in Chinese with English Abstract)

[16] 张欣，张洪江，张福明，等. 西南山区农地土壤前期含水量对优先流的影响[J]. 水土保持学报，2014，28(2)：1－7，14. Zhang Xin, Zhang Hongjiang, Zhang Fuming, et al. Effect of antecedent soil moisture on preferential flow in agricultural land of southwest mountains[J]. Journal of Soil and Water Conservation, 2014, 28(2): 1－7, 14. (in Chinese with English Abstract)

[17] 闫加亮，赵文智，张勇勇. 绿洲农田土壤优先流特征及其对灌溉量的响应[J]. 应用生态学报，2015，26(5)：1454－1460. Yan Jialiang, Zhao Wenzhi, Zhang Yongyong. Characteristics of the preferential flow and its response to irrigation amount in oasis cropland[J]. Chinese Journal of Applied Ecology, 2015, 26(5): 1454－1460. (in Chinese with English Abstract)

[18] 张财宝，刘目兴，王文德，等. 三峡库区森林土壤优先流染色特征[J]. 水土保持学报，2012，26(2)：80－84. Zhang Caibao, Liu Muxing, Wang Wende, et al. Dyeing characteristic of preferential flow under forestland in the Three Gorges Reservoir area[J]. Journal of Soil and Water Conservation, 2012, 26(2): 80－84. (in Chinese with English Abstract)

[19] 高朝侠，徐学选，赵传普，等. 土壤初始含水率对优先流的影响[J]. 中国水土保持科学，2014，12(1)：46－54. Gao Zhaoxia, Xu Xuexuan, Zhao Chuanpu, et al. Effect of initial soil water content on preferential flow[J]. Science of Soil and Water Conservation, 2014, 12(1): 46－54. (in Chinese with English Abstract)

[20] 刘目兴，杜文正. 山地土壤优先流路径的染色失踪研究[J]. 土壤学报，2013，50(5)：871－880. Liu Muxing, Du Wenzheng. To investigate soil preferential flow paths in mountain area using dye tracer[J]. Acta Pedologlca Sinica, 2013, 50(5): 871－880. (in Chinese with English Abstract)

[21] 徐宗恒，徐则民，官琦，等.不同植被发育斜坡土体优先流特征[J]. 山地学报，2012，30(5)：521－527. Xu Zongheng, Xu Zemin, Guan Qi, et al. The characteristic of preferential flow in different vegetated slope soils[J]. Journal of Mountain Science, 2012, 30(5): 521－527. (in Chinese with English Abstract)

[22] 陈晓冰，张洪江，李世友，等. 紫色砂岩区不同植被类型土壤优先流特征及其影响因素[J]. 中国水土保持科学，2014，12(6)：42－49. Chen Xiaobing, Zhang Hongjiang, Li Shiyou, et al. Characteristics

and influencing factors of preferential flow in different vegetation types of purple sandstone regions[J]. Science of Soil and Water Conservation, 2014, 12(6): 42－49. (in Chinese with English Abstract)

[23] 吴庆华，张家发，蔺文静，等. 土壤水流模式染色剂示踪及优先流程度评估[J]. 农业工程学报，2014，30(7)：82－90. Wu Qinghua, Zhang Jiafa, Lin Wenjing, et al. Appling dyeing tracer to investigate patterns of soil water flow and quantify preferential flow columns[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(7): 82－90. (in Chinese with English Abstract)

[24] 盛丰，张利勇，王康. 土壤大孔隙发育特征对水和溶质输移的影响[J]. 土壤，2015，47(5)：1007－1013. Sheng Feng, Zhang Liyong, Wang Kang. Study on developmental characteristics of macropores and their effects on soil water flow and solute transport with tracer infiltration experiments[J]. Soils, 2015, 47(5): 1007－1013. (in Chinese with English Abstract)

[25] Genuchten V, Th M. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44 (5): 892－898.

[26] 盛丰，方妍.土壤水非均匀流动的碘-淀粉染色示踪研究[J]. 土壤，2012，44(1)：144－148. Sheng Feng, Fang Yan. Study on preferential soil water flow using iodine-starch staining method[J]. Soils, 2012, 44(1): 144－148. (in Chinese with English Abstract)

[27] 盛丰. 土壤优先流的活动流场模型理论研究[D]. 广州：中山大学，2009. Sheng Feng. Study on the Active Region Model for Preferential Flow in the Unsaturated Soil[D]. Guangzhou: Sun Yat-sen University, 2009. (in Chinese with English Abstract)

[28] Kamra S K, Lennartz B, Genuchten V, et al. Evaluating non-equilibrium solute transport in small soil columns[J]. Journal of Contaminant Hydrology, 2001, 48(3/4): 189－212.

[29] 郭会荣，靳孟贵，王云. 基于室内土柱穿透实验的优先流定量评价[J]. 地质科技情报，2009，28(6)：101－106. Guo Huirong, Jin Menggui, Wang Yun. Quantitative evaluation of preferential flow based on laboratory breakthrough experiments of soil columns[J]. Geological Science and Technology Information, 2009, 28(6): 101－106. (in Chinese with English Abstract)

[30] 李小明，谢祥俊，刘建兴. 概率与数理统计[M]. 北京：高等教育出版社，2004：141－147.

[31] 孙洪泉. 分形几何及其分形插值研究[J]. 河北工业大学学报，2002，31(1)：56－60. Sun Hongquan. Fractal geometry and study on fractal interpolation [J]. Journal of Hebei University of Technology, 2002, 31(1): 56－60. (in Chinese with English Abstract)

[32] 许领，戴福初，邝国麟，等. 台缘裂缝发育特征、成因机制及其对黄土滑坡的意义[J]. 地质论评，2009，55(1)：85－90. Xu Ling, Dai Fuchu, Kwong A K, et al. Characteristics and forming mechanisms of the plateau-edge cracks and their significance to loess landslides[J]. Geological Review, 2009, 55(1): 85－90. (in Chinese with English Abstract)

Quantitative determination of preferential flow characteristics of loess based on nonuniformity and fractional dimension

Pan Wangsheng1,2, Xu Yufeng1, Lu Yudong2, Gao Li’an1, Yao Xing1

(1.558000,; 2.710054,)

Understanding the seepage characteristics of loess preferential flow is important for loess landslide risk control. In order to study the seepage characteristics of loess preferential flow, in this study, eight test pits were designed in 2 regions of the abandoned farmland in Nanyuan Dongfeng village, Jingyan county, China (108°50′48″E, 34°29′25″N). The soil was developed in loess parent material. In each region, soil texture was homogenous without obvious macropore and cracks. The test pits were labeled with 1#-8#. In region I, the first 3 pits had same size, but different designed infiltration amount with 30, 60 and 90 mm, respectively. The 4# pit was similar with the 2# pit, but the former had high initial soil moisture. The 5#, 6# and 7# were same with 1#, 2# and 3#, respectively but in the region II. The 8# pit was similar with 4#, but had a bigger size. The dye tracer method was conducted and the soil profile was pictured. The images after binarization were used for preferential flow characteristics analysis. The infiltration depth and amount non-homogeneous coeffeicients were determined. The fractal dimension and fractal feature parameter were also determined. The results showed that infiltration had an obvious impact on the infiltration depth. The nonuniformity of the preferential flow infiltration depth became more obvious with increasing infiltration. However, the nonuniformity of the preferential flow infiltration depth was less obvious when the initial moisture content was high. The development of the preferential flow was lower, its velocity was higher, the average infiltration was greater and the fractal dimension was smaller. The loess porosity size also significantly influenced the correlation coefficient of the preferential flow infiltration depth. The nonuniformity of the infiltration coefficient and the nonuniformity of the preferential flow infiltration depth became more obvious and the fluctuation range of depth thresholds was greater when porosity increased. The test scale of loess for the same treatment did not show an appreciable effect on the fractal dimension of the wet peak trace. Within the 0-0.5 times of maximum infiltration depth of preferential flow in southern tableland in Jingyang County, when the value of the fractal characteristic was high, the nonuniformity of the preferential flow was higher, and the preferential flow was more developed. Without obvious preferential flow seepage channel, the maximum infiltration depth was less than 120 cm under irrigation water volume of 90 mm. Considering normal evaporation and no crack, we considered that the surface irrigation water was not easy to directly lead to the rise of ground water level. Therefore, the preferential flow plays an important role in the whole process from the surface water to the groundwater. At the same time, the influence of preferential flow on loess landslide should not be ignored.

infiltration; soils; fractal dimensions; loess; preferential flow; tracer test; seepage characteristics

10.11975/j.issn.1002-6819.2017.03.019

P642.13+1;S152.2

A

1002-6819(2017)-03-0140-08

2016-03-19

2016-09-10

国家自然科学基金项目（40372114）；贵州省教育厅创新群体重大研究项目（黔教合KY字[2016]054）；贵州省教育厅创新群体重大研究项目（黔教合KY字[2016]055）。

潘网生，男，江苏镇江人，博士，从事地质灾害与生态环境研究。都匀黔南民族师范学院，558000。Email：450392404@qq.com。

潘网生，许玉凤，卢玉东，高礼安，姚 兴. 基于非均匀性和分形维数的黄土优先流特征定量分析[J]. 农业工程学报，2017，33(3)：140－147. doi：10.11975/j.issn.1002-6819.2017.03.019 http://www.tcsae.org

Pan Wangsheng, Xu Yufeng, Lu Yudong, Gao Li’an, Yao Xing.Quantitative determination of preferential flow characteristics of loess based on nonuniformity and fractional dimension[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(3): 140－147. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.03.019 http://www.tcsae.org