利用高斯定理求空心球体引力场

余泽西

(北京市昌平新东方外国语学校 北京 102206)

利用高斯定理求空心球体引力场

余泽西

(北京市昌平新东方外国语学校 北京 102206)

针对现阶段AP物理教学中引力有关定律推导问题，采取与以往建立微分式不同的方法，即利用高斯定律来求解空心引力场值：地球谐振子模型和空心球壳，为广大教师提供一个新的授课思路．

AP教学 引力场 空心球体 高斯定律

1 引言

现阶段物理教学中，对于空心球体内部引力场值问题，教师一般采用建立微分方程的方法，然而这种方法虽建立简单，但是求解困难，因为涉及两个变量θ和R使得学生难以求解[1]．如果我们可以利用引力场是保守力场这一事实将其与电磁场做类比，从而使学生可以方便地求解球形引力场的场强．在AP力学[2]的教学中，引力场求解部分主要集中在牛顿的经典力学，也就是说，引力与质量是成线性关系的．而对于本文所讨论电磁学中，我们使用简化版描述静电场的麦克斯韦方程[3]．这是由于AP课程主要是针对于未参加大学学习即将进入美国大学的学生，他们微积分知识较为薄弱，所以在美方标准课标中，去除了难以令学生理解的散度概念和复杂的算符表达．

2 二者的相似性

3 求地球引力系数

在AP物理学中，简化静电场公式为

这里E是电场强度，Q是电荷量．

通常的我们称ε0为静电系数，但并不知道在引力场的高斯定理中质量与G的关系，也就是说“引力系数”．但在确定二者的相似性后，我们可以通过联立库仑定律和万有引力公式来求解引力场中的高斯定理的质量系数．

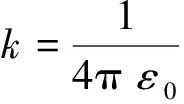
∮g·dA=4πGM

(1)

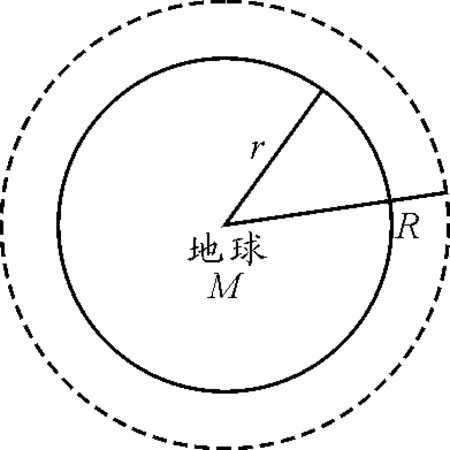
图1 求地球引力系数附图

证：

(1)地球的物质分布均匀，即密度处处相等

(2)地球是完美实心球体

(3)∀是引力场强系数，g是引力场强，地球半径为r，质量为M，高斯面半径为R，在R处，则有

∮g·dA=4πGM

(2)

由于是完美球体，力场强度在R上处处相等

g·∮dA=4πGM

球表面积为

S=4πR2

(3)

将式(3)代入式(2)有

(4)

高斯引力和万有引力公式结论一致，证毕．

在考题中学生一般会遇到高斯面内质量随高斯面的大小改变而改变的情况，那么此时如果简化高斯定理中的变量是质量密度，就会显得更有效．而且在AP物理中，问题中的质量源一般是均匀的(密度在 球体内处处相等)，所以

∮g·dA=4πGM=4πGρV

(5)

这里，V是体积．

4 该方法在习题中的应用

现在针对真实出现的考题，做举例说明．

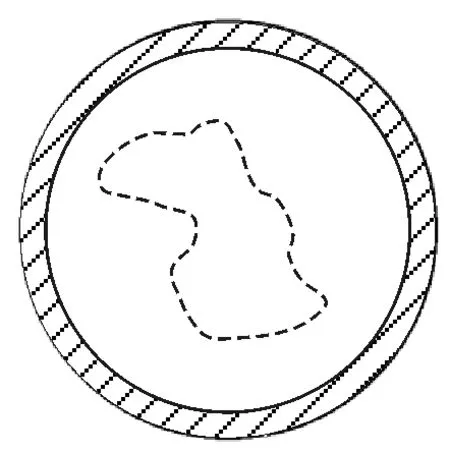
4.1 求中空隧道的引力场值(地球谐振子模型)

图2 地球谐振子模型

已知：

(1)地球质量分布均匀；

(2)中间隧道十分微小；

(3)地球质量为M，密度为ρ；高斯面半径为r.

求：在r

解：如图2所示，利用球形对称，我们利用式(5)建立式子

∮g·dA=4πGρV

∮dA=4πr2

约分整理得

(6)

式(6)结果表明，引力场强度和半径成线性关系(Linear relationship)可以发现除了r是变量之外，其他符号表示的量均为常量．由此我们可以得到空心隧道引力场强度变化是随着半径成线性变化的结论．

4.2 求空心球壳的引力场值

利用高斯定理，原本复杂的空心球体计算也大大简化，如图3所示.

图3 空心球壳

由于在高斯面内没有质量分布,其质量M为零，式(5)可列为

∮g·dA=4πG·0

解得

g=0

由于中心无源，本题目的难度大大简化，物体在空心球壳内部的引力为零.

5 总结

综上所述，可以得到以下几个结论：

(1)引力系数为∀=G·4πρ=4πGM；

(2)隧道模型引力场强度随半径成线性递增；

(3)空心球体内部引力场值处处相等.

可以发现, 由于球形对称的结构, 引力场用高斯面可以非常方便的被求解． 且相比于牛顿的质点方法，这种对于力场的直观呈现可以使学生更好的抓住要点，和形成明确的物理直觉．而且由于AP物理考题中，物理题大多都为本文所提及球形对称，所以该方法可以让学生更快的得到结果．

1 陈小红 罗琬华. 西南大学物理科学与技术学院.物理通报，2014(05):116～117

2 Parker W,Mosborg S,Bransford J,et al. Rethinking Advanced High School Coursework:Tackling the Depth/Breadth Tension in the AP "US Government and Politics" Course.Curriculum Studies,2011, 43(4):1～27.

3 S. Nesseris and L.Perivolaropoulos. Department of Physics,University of Ioannina,Greece.Physical Review D Particles & Fields,2006,73(10):3 511

4 Exner P.Analysis on graphs and its applications:Issac Newton Institure for Mathematical Sciences,Cambridge,UK,January 8-June 29, 2007.American Mathematical Society,2008

5 Gravity G L F.Gauss′ Law for Gravity.Alphascript Publishing,2010

6 Ragains P.Cracking the AP Physics 2 Exam,2016 Edition.Public Finance Review,2015,22(3):366～382

Gauss′sLawtoProveHollowSphere′sGravitationalField

YuZexi

(BeijingchangingNewOrientalFLS，Beijing102206)

considering the current AP teaching problem about gravitational field conduction, I used Gauss′s Law to prove two models, harmonic oscillator earth and hollow sphere, instead of conventional differential equation. This method, I hope, can provide teachers a new way to prove for students.

AP teaching;gravitational field;hollow sphere;Gauss′s Law

2016-08-23)