小学数学教学中数学思想的渗透探析
2017-03-02苏泽
苏泽
摘 要:数学是众多科学的基础,对于提升学生的逻辑思维能力是非常有效的,要做好数学的教学,就要从娃娃抓起,小学的教学就成为了重点。我们在教学过程当中,要注意数学思想的渗透,让学生善于使用数学思想解决问题。本文对相关知识进行了论述,希望对小学数学的教学有所帮助。
关键词:小学数学 数学思想 教学
引言
数学思想是人类思想文化宝库中的瑰宝,也是推动人类进步的关键要素。在小学数学的教学过程当中,我们要帮助学生理解数学思想,吃透数学思想,运用数学思想,从而提高他们的数学学习能力,提高学校的教学水平。教师要对数学思想引起足够的重视,引导学生运用数学思想解决问题。笔者根据自己的经验,对小学数学教学中如何渗透教学思想提供了一定的建议,希望能够抛砖引玉。
一、数形结合思想的渗透
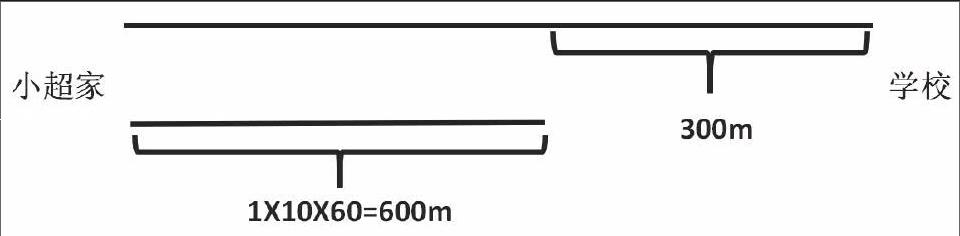
数形结合思想是数学教学当中最为常用的思想之一,也是帮助学生更好学习数学的重要媒介。從狭义上来说,数学本身就是一门以数字、字母和图形组成的学科,解题的过程中,数字离不开图形,图形离不开数字,所以,在教学过程当中,我们要将数字和图形充分的结合到一起,从而让学生理解更加深刻。近年来,随着新课改的不断深入,我国对数形结合思想的运用越来越成熟、灵活,教师也将此方法越来越多的利用到了小学数学的教学当中。小学生大多处于6-13岁的阶段,对于图形的敏感程度是非常高的,通过数形结合思想的教学,往往可以将复杂的问题简单化,也能使学生的脑中形成一套完整的体系,有助于他们更好的开展学习。在小学数学的教学当中,数形结合思想最为常见的例子就是速度与距离的问题,我们可以通过绘制线段的形式来帮助学生进行解题。比如,我们举一个应用题的例子,小明与小超是好朋友,天天一起上学,由于小明家比小超家远,小明天天先去小超家,再一起到学校。今日,小明骑自行车上学,而小超步行上学,由于小明起床较晚,所以小超先行出发,以1m/s的速度向学校前进,而当小明赶到了小超家的时候,发现小超已经出发了10分钟,这时小明以6m/s的速度追赶小超,这时小超距离学校还有300米,问,小明和小超谁先到达学校呢?这个问题看起来比较复杂,但是通过图形的绘制,整个过程就非常明确了,流程如下所示:
小明在小超家时,小超已经走了600米,此时小明以6m/s的速度往学校出发,总路程为900m,那么900÷6=150s,小明到达学校还需要150s,而小超到达学校的时间为300÷1=300s,所以,小明虽然后走,但是由于速度优势,将率先到达学校。从这个例子中我们可以看出,利用线段等图形帮助解题的效率是很高的,能够将繁琐的问题转化为简单的形式,方便了学生的理解。数形结合的思想是数学教学中应用最为广泛的思想,要求教师备课时要将这个思想融入到理论教学和例题,锻炼学生的逻辑思维,提高教学的效率。[1]
二、等价转化思想的渗透
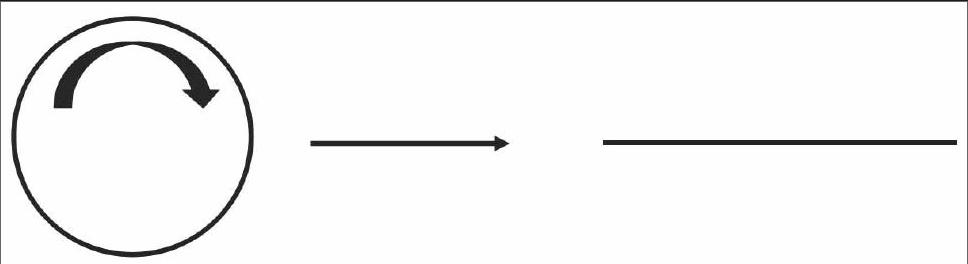
除了数形结合思想之外,等价转化思想也是我们最为常用的方法,等价转化思想,顾名思义,就是为了解决同一的问题的两种不同的方法,将复杂的情况转化为了简单的情况,这样,就可以将问题更好的解答。在数学的教学当中,有很多问题比较难以理解,解答起来比较困难,但是,我们可以将题目的内容做一等价的转化,这样,就能使问题得到很好的解决。等价转化思想的核心就是将未知的问题转化为已知的问题进行解答,可以本来难以回答的问题变得简单明了。我们举一个非常简单的例子,在研究圆形的周长的时候,我们一开始无从下手,不知道该怎样解决,而我们把求圆形的周长换成求线段的长度,我们就可以利用我们所学的知识进行解决了。我们用绳子做成圆形,然后用剪刀将圆形的绳子剪开一个小口,将绳子捋直,然后使用卡尺对绳子的长度进行测量,得到的结果就是我们所要的圆形的周长。具体图示如下所示:[2]
通过这种等价转化的思想,我们就可以把比较难以计算的圆形周长转化为了可以计算的线段长度了。从这个例子当中,我可以清楚的看出,运用等价转化思想,可以使比较困难的问题转化为一个相对简单的问题,用我们掌握的知识来进行解答,在日常的教学当中,我们要教育学生灵活的运用这种思想,从而能够提高他们的逻辑思维能力,同时,也可以触类旁通,提高数学素养和能力,为他们今后的学习和生活打下坚实的基础。[3]
三、直观数学思想的运用
以上两种教学思想是应用非常广泛的,同时,还有一些其他的数学思想也能够有效的帮助学生提升逻辑思维能力,养成良好的数学习惯,从而更好的进行解题。小学生处于数学学习的基础阶段,数学思想对他们的影响将是非常重大的,我们要利用好这些数学思想,帮助学生提高数学学习能力。直观数学思想就是非常常用的数学思想之一,所谓直观,就是让学生的思想能够直接的接触题目,给予他们真正的想象空间和思考时间,并且在整个课堂教学的过程中,要不断的创设宽松、热烈的研讨气氛,教师要解答学生提出的具有针对性的问题,无论在解题方法和解题策略上面都要需要巧妙的答疑解惑,激发学生的学习积极性的一种数学思想。例如,学习三角形、四边形变化相关内容的时候,教师要尊重学生自己的想法,可以在学生的学习思维基础上不断的引导和启发,对比出图像的不同之处。培养学生的想象能力对学生直观思维的培养有推助作用。再比如,学习平面图形面积计算等相关内容的时候,因为单纯的图像记忆让学生感觉很困难,如果运用想象能力,引导学生把图象想象成某一个特定的图形,这样记忆起来就更加的深刻。我们要利用好直观数学思想,让学生的思维更加深入而简练,锻炼他们的解题能力。[4]
结语
在小学数学的学习中渗透教学思想是非常必要的,我们要充分的利用好数形结合思想、等价转化思想、直观数学思想等,让这些数学思想真正的在学生的脑子里生根发芽,从而更好的帮助他们进行学习,提高数学思维能力。
参考文献
[1]戴依敏. 试论小学数学教学中数学思想的渗透[J]. 教育观察(中下旬刊),2015,30:101-102.
[2]王伟政. 小学数学教学中数学思想方法的渗透实践[J]. 学周刊,2016,25:255-256.
[3]姜嫦君,刘静霞. 小学数学教学中数学思想方法的渗透[J]. 延边教育学院学报,2010,02:106-108.
[4]陈祥彬. 在小学数学教学中渗透数学思想方法[J]. 课程·教材·教法,2010,07:37-41+36.
