基于非解析正交矩的图像分析

赵远阳, 付 波, 赵熙临, 范秀香, 郭 浩

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

基于非解析正交矩的图像分析

赵远阳, 付 波, 赵熙临, 范秀香, 郭 浩

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

为进一步提高正交矩的图像特征表达能力，根据零点采样原理，认为权函数是影响正交多项式零点分布的关键因素，采用正交化准则与数值方法相结合的手段求取非解析正交多项式，从而构造高性能的非解析正交矩，实验验证表明该方法是有效的。

正交化原则；数值方法；非解析正交多项式；非解析正交矩

20世纪80年代以来，以Zernike矩和Legendre矩为代表的正交矩逐步成为图像处理与模式识别领域的一类重要特征表达手段[1]，探索图像理解与分析的新理论、新方法成为近30年图像矩理论的研究热点。随后，Y.L.Sheng[2]、平子良[3- 5]、阿木古愣[6, 7]、M. Pawlak和S.X. Liao[8, 9]、R. Mukundan[10-12]、舒华忠[13-15]、付波[16]、P.T. Yap[17]等提出了正交Fourier-Mellin矩、Fourier-Jacobi(p=4,q=3)矩、Hahn矩、Chebichef矩、改进Legendre矩、Krawtchouk矩等多种高性能矩，并研究了正交矩的多畸不变性、抽样性能、误差抑制以及算法效率等不同因素对其特征表达能力的影响。

已有研究成果表明，正交多项式的抽样性能，即正交多项式的零点分布及其分布密度对正交矩的图像特征表达能力有重要影响[2]。正交矩基函数的零点数目和密度与其描述图像高空间频率成分的能力密切相关[3-7,15,16]，即n阶多项式的零点数目和位置代表着该阶图像矩对图像的抽样频率和抽样位置，对应的低阶矩主要抽取总轮廓特征，而高阶矩捕获高频细节信息。研究者可以通过改进或研究零点分布更好的正交基函数来改善正交矩的性能，正交矩的零点越多，矩的特征表达能力越强，而且较均匀零点分布的正交矩在表现图像的全局特征上效果更好，正交Fourier-Mellin矩[2]、Fourier-Chebyshev矩[3]、Fourier-Jacobi(p=4,q=3)矩[6]、Fourier-Jacobi矩[4]以及改进Legendre矩[17]等高性能正交矩就是基于此原理提出的。然而阿木古楞[6]等人的研究也表明，由于固定零点会造成该零点附近重构效果退化，该类零点只能设置在定义域的两端；其次，经典解析正交多项式的种类有限，限制了零点分布的可选择性。因此，如果想进一步提高正交矩的特征表达能力，必须另辟蹊径，寻找新的方法求解具有更优零点分布的正交多项式。

正交矩的核是正交多项式，按照Askey的研究[18-20]，经典正交多项式分为wilson连续正交多项式与Racah离散正交多项式两大类。Jacobi多项式归于Wilson多项式，而Hahn多项式、Krawtchouk多项式等属于Racah多项式的特例。20多年来，围绕这些具有解析表达的经典正交多项式提出了多种正交矩如Legendre矩、Zernike矩、径向Chebyshev矩、径向Jacobi矩、Tchebichef矩、Krawtchouk矩、Hahn矩、Racah矩等。受数学基础研究的限制，具有解析表达的正交多项式不仅种类有限而且极难构造，这一情况极大限制了正交矩的研究。自Q.Y. Zhu等提出离散Racah矩后，鲜见新的高性能正交矩的报道，一个重要原因就是正交多项式解析表达的限制。由于正交多项式的零点分布局有渐进特性[19]，仅从有限的经典解析正交多项式寻找优化零点分布的手段显得力不从心，需要探索生成新正交多项式的方法。

因此，本文从这些研究成果与思路出发，突破解析正交多项式的局限，采用数值方法求解正交多项式，将更灵活地配置正交多项式的零点分布，以构造具有更好图像特征表达能力的正交矩。

1 图像正交矩

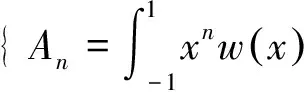
其中,展开系数正交函数系ηnm由

式中ηpq称为f(x,y)的正交矩。

2 非解析正交矩

2.1 正交化准则结合数值方法构造带权非解析正交多项式

定义区间[-1,1]内的连续权函数w(x)及其与xn的内积

权函数w(x)对应的正交多项式

(1)

由多项式正交化准则，Pn(x)应满足

(2)

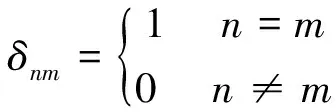
也即Pn(x)应满足

(3)

式(3)可写为：

An+lbn+An+l-1bn-1+…+Al+1b1+Alb0=0

(4)

其中l

(5)

通过松弛叠代法，求取式(5)在可以求取已知bn条件下的数值解，这样求得满足式(2)的多项式Pn(x)。由求模公式得

(6)

2.2 非解析正交矩

式(1)和式(6)可构造正交矩

其反变换公式为

(7)

该方案虽然是以区间[-1,1]为例得出，它也适合于其他定义域形式如[0,1]。

2.3 通过权函数调整正交多项式零点分布

正交多项式的零点分布具有渐进特性，即零点分布密度总是沿变量的某一方向增加。根据对相关研究成果的分析，权函数是影响正交多项式零点分布的关键因素。同时考虑权函数零点对重构效果的影响，本文对权函数的设计定义以下原则：

1)权函数不设零点或将零点设置在定义域的端点；

2)设计权函数形态，使正交多项式零点分布更平均。

3 实验验证

根据以上对正交多项式从零点数量和零点分布密度两个方面的分析可知，通过设计不同特性的权函数，可以按照实际应用需求合理安排正交多项式的零点分布，使低阶正交矩包含更多的图像细节，从而增强正交矩的特征表达能力。

本文分析一类较特殊的正交多项式，令权函数w(x)>0关于y轴对称，按照式(2)到式(5)求解P2(x)得b1=0，同时由式(5)可得：

b2A2+b0A0=0

即

代入式(5)可得二阶零点：

(8)

从式(8)项目组推断，权函数w(x)的内积A0越小，零点就越靠近原点；反之，则远离原点。根据该结果，项目组构造四个权函数(图1)：

图 1 四个权函数的示意图

从图1以及实际计算可知，四个权函数的0阶内积的大小顺序为

(a)带权w1(x)正交多项式

(b)带权w2(x)正交多项式

(c)带权w3(x)正交多项式

(d)带权w4(x)正交多项式图 2 四类正交多项式示意图

图 3 四类正交矩重构效果图

图 4 四类正交矩归一化均方误差

根据式(8)，对应0阶内积越小的权函数，对应正交多项式的二阶零点也越靠近原点。因此，高阶正交多项式的零点也相应向原点移动。由数值方法求解方程(5)可以得到四个权函数对应的非解析正交多项式，如图2分别画出四个正交多项式的1-6阶示意。从图中可以清晰看到，0阶内积越小的权函数，对应的正交多项式零点分布越均匀。按照零点分布密度与重构性能的关系，应有w4(x)对应的正交多项式具有较均匀的零点分布，其对应的正交矩在四类情况中应具有最好的重构效果。图3和图4记录了四类正交矩对一20×20图像“我”的重构效果与归一化均方误差

图5和图6结果显示：带权w4(x)正交矩在四类矩中具有最好的重构效果。试验结果验证了本项目研究思路的可行性与正确性，即正交化与松弛迭代法结合的非解析带权正交多项式算法是可行的，权函数可以改变零点分布，具有较均匀零点分布的正交矩具有更好的整体重构性能。

4 结论

根据零点采样原理，认为权函数是影响正交多项式零点分布的关键因素，采用正交化准则与数值方法相结合的手段求取非解析正交多项式，从而构造高性能的非解析正交矩。虽然该方法不能完全完成任意权正交多项式的求解，但对于目前使用较多的多项式类权具有较好的求解效果，实验验证表明该方法是有效的。但是对于式(5)的数值求解存在计算效率的问题，大型矩阵方程的求解效率仍是本方法需要考虑的问题。

[1] Teague M. Image analysis via the general theory of moments[J]. J. Opt. Soc. Amer., 1980, 70(8): 920-930.

[2] Sheng Y L, L X Shen. Orthogonal Fourier-Mellin moments for invariant pattern recognition[J]. J. Opt. Soc. ,Am. (A), 1994, 11(6): 1748-1757.

[3] Ping Z L, R G Wu, Y L Sheng. Image description with Chebyshev-Fourier moments[J]. J. Opt. Soc. Am. (A), 2002, 19(8): 1748-1754.

[4] 任海萍, 平子良，博午日亘. Image Description with Jacobi-Fourier Moments[J]. 光学学报, 2004, 24(1): 5-10.

[5] Ping Ziliang, Haiping Ren, Jian Zou, et.al. “Generic orthogonal moments: Jacobi-Fourier moments for invariant image description[J].” Pattern Recognition, 2007, 40(4): 1245-1254.

[6] Amu G L, Hasi S R, Yang X Y, et al. Image Analysis by Pseudo-Jacobi(p=4,q=3)-Fourier Moments[J]. Applied Optics, 2004, 43(10):2093-2101.

[7] 阿木古楞, 哈斯苏荣, 利民, 等 . 用变形雅可比(p=4, q=3)-傅立叶矩描述红花粉末的显微图像[J]. 内蒙古农业大学学报(自然科学版), 2006, 27(3): 129-131.

[8] Liao S X , Pawlak M. On image analysis by moments[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(3): 254-266.

[9] Xin Y Q, Pawlak M, and Liao Simon. Accurate computation of zernike moments in polar coordinates[J]. IEEE Trans. On Image Process, 2007, 16(2): 581-587.

[10] Mukundan R, Ong S H, Lee P A. Image analysis by Tchebichef moments[J]. IEEE Transactions on Image Processing, 2001, 10(9): 1357-1364.

[11] Mukundan R. Some computational aspects of discrete orthonormal moments[J]. IEEE Transactions on Image Processing, 2004, 13(8): 1055-1059.

[12] Mukundan R. Radial tchebichef invariants for pattern recognition[C]. Proc. of IEEE Tencon Conference Tencon05, Melbourne, Nov 2005: 2098-2103.

[13] 秦磊, 舒华忠, 於文雪,等. Legendre矩的两种快速算法[J]. 电子学报, 2004, 32(1):25-28.

[14] Gu J, Shu H Z, Toumoulin C, et al. A novel algorithm for fast computation of Zernike moments[J]. Pattern Recognition, 2002, 35(12): 2905 - 2911.

[15] Zhu H Q, Shu H Z, Liang J, et al. Image analysis by discrete orthogonal Racah moments[J]. IEEE Trans. on Signal Processing, 2007, 87(4): 687-708.

[16] Fu B, Zhou J Z, Li Y H, etal. Image analysis by modified Legendre moments[J]. Pattern Recognition, 2007, 40(2): 691-704.

[17] Yap P T, Raveendran P, Ong S H. Image analysis by Krawtchouk moments[J]. IEEE Transactions on Image Processing, 2003, 12(11): 1367-1377.

[18] Temme N M. The askey scheme for hypergeometric orthogonal polynomials viewed from asymptotic analysis[R]. Technology Report, MAS-R0005, 2000.

[19] Dunkl C F, Xu Y. Orthogonal polynomials of several variables[M]. Cambridge University Press, 2001.

[20] Goovaerts M J, Wimp J, Wuytack L, et al. Applications and numerical analysis[J]. Journal of Computational and Applied Mathematics-Special issue: nonlinear problems with blow-up solutions，1998, 96(2):1404-1416.

[责任编校： 张岩芳]

Image Analysis Based on Non-Analytic Orthogonal Moments

ZHAO Yuanyang, FU Bo, ZHAO Xilin, FAN Xiuxiang, GUO Hao

(SchoolofElectrical&ElectronicEngin.,HubeiUniv.ofTech.,Wuhan430068,China)

In order to enhance the feature extraction capabilities of orthogonal moments, based on the theory of zero sampling, we think that the power is the key factor in influencing the zero distribution of orthogonal polynomials. And the orthogonality criterion and numerical algorithm are used to resolve non-analytic orthogonal polynomials and construct the non-analytic orthogonal moments. The experimental results show that the proposed moments have superior performance.

Orthogonality criterion, Numerical method, non-analytic orthogonal polynomials, non-analytic orthogonal moments

2016-01-06

国家自然科学基金项目(61072130)，武汉市科技攻关计划项目(2013012401010845)，湖北工业大学基金项目(BSQD12107

赵远阳(1990-)， 男， 湖北武汉人，湖北工业大学硕士研究生，研究方向为图像数数值稳定性分析

1003-4684(2017)01-0056-04

TP75

A