翼型对水下滑翔机滑翔性能影响分析

徐世勋 刘玉红 朱亚强 王延辉

1.机构理论与装备设计教育部重点实验室，天津，3000722.天津大学机械工程学院，天津，300072

翼型对水下滑翔机滑翔性能影响分析

徐世勋1,2刘玉红1,2朱亚强1,2王延辉1,2

1.机构理论与装备设计教育部重点实验室，天津，3000722.天津大学机械工程学院，天津，300072

选用NACA 4位数翼型，采用计算流体力学方法分析了翼型对水下滑翔机滑翔经济性和稳定性的影响。研究结果表明，合适的翼型可以极大地提高滑翔经济性，但对滑翔机静稳定性的提高并不明显；对于非对称翼型，翼型的弯曲程度和弯曲方向对滑翔经济性和静稳定性的影响均很大。在此基础上，并结合工程实际，提出了变后缘柔性机翼方案，通过数值模拟试验验证了所提出方案的可行性。研究成果为水下滑翔机柔性机翼的设计提供了理论参考。

水下滑翔机；翼型；滑翔经济性；滑翔稳定性；变后缘柔性机翼

0 引言

水下滑翔机是通过调节自身浮力进行驱动的新型无人水下航行器，其续航能力强、噪声小、制造成本低，因而被广泛应用于海洋科学研究、海洋环境监测以及军事侦查等领域[1-3]。水下滑翔机机翼在一定攻角下能产生水动升力，从而将滑翔机的净浮力转换为前进驱动力。合适的机翼设计可以提高滑翔机的航行性能(滑翔经济性和滑翔稳定性)，进而减少能耗、提高航程。

为改进水下滑翔机的性能，研究者们分别从机翼结构参数、机翼布局等方面开展了研究，甚至还开展了可变机翼的研究。武建国等[4]采用正交试验的方法研究了机翼弦长、安装位置、后掠角以及展弦比对滑翔机经济性和稳定性的影响；赵宝强[5]分析了滑翔机水平固定机翼的展弦比、根梢比、后掠角等设计参数之间的关系并进行了优化，在此基础上设计了柔性机翼，以提高滑翔机的稳定性；宫宇龙等[6]对实验尺度水下滑翔机机翼的安装位置、后掠角、展长、展弦比和根梢比这5个设计参数进行了分析，并设计了一种适用于试验尺度滑翔机的高升阻比水平机翼。在可变机翼的研究方面， ARIMA等[7]设计并开发了可翻转机翼的滑翔机模型Alex。ISA等[8]建立了拥有可变机翼和方向舵的水下滑翔机动力学模型，并进行了运动仿真。英国国家海洋中心研制的AutosubLR带有分体机翼，可以实现机翼的伸长和缩短，可改变机翼位置，并实现了机翼的翻转[9]。YANG等[10]设计了可以改变展弦比、后掠角以及翻转角的可变机翼，提高了滑翔机的经济性、稳定性和机动性。田文龙等[11]通过对滑翔机机翼翻转角的控制，提高了滑翔机的滑翔速度和机动性。

水下滑翔机作为水下“飞机”，其机翼的形状、尺寸及布局为水下滑翔机在水中滑翔提供着必需的升力及水动力，机翼每个参数的改变都会极大地改变水下滑翔机周围的水动布局。本文在前期研究基础上，以天津大学研制的“海燕”混合驱动水下滑翔机为对象，研究机翼翼型对水下滑翔机滑翔经济性和稳定性的影响，并提出了软体柔性机翼的概念设计模型。研究成果一方面为水下滑翔机性能优化提供理论参考，另一方面也为软体柔性机翼的设计提供基础理论支持。

1 翼型参数

机翼平行于飞行器对称面或垂直于前缘的剖面形状称为翼型。在现有翼型资料中，美国国家航空咨询委员会(NACA)开发的NACA翼型系列较为丰富。国内外现有的水下滑翔机机翼多为矩形平板对称翼型[12-15]。由于水下滑翔机不同航行模式下所需的水动力不同，为研究翼型对滑翔机不同航行模式下航行性能的影响，本文选取对称和非对称两类翼型进行试验,分别考察翼型厚度和翼型弯度对滑翔机航行性能的影响。

水下滑翔机的滑翔速度较低，本文以NACA 4位数翼型族作为研究对象。NACA 4位数翼型是NACA最早建立的一个低速翼型系列[16]，翼型如图1所示。翼型标记为 NACAXYZZ，其中，X表示相对弯度(翼型最大弯度相对于弦长的百分数)，Y表示最大弯度相对位置(翼型最大弯度位置位于弦长的百分数)，ZZ表示相对厚度(翼型最大厚度相对于弦长的百分数)。即

X=h/cY=xh/cZZ=t/c

其中，h为中弧面与弦线间的最大距离；c为翼型弦长；xh为最大弯度的位置与前缘的距离；t为翼型的最大厚度。例如NACA1412的含义即翼型最大弯度为弦长的1%，最大弯度位置在始于前缘的40%弦长处，最大厚度为弦长的12%。为了便于试验对比，本文所选的6种翼型最大厚度均在弦长30%处。

图1 NACA 4位数翼型参数Fig.1 Parameters of NACA 4-digit airfoil

对称翼型组机翼型号分别为NACA0006、NACA0012、NACA0018，本文中，具有矩形翼形的平板翼也归为对称翼型组；非对称翼型组机翼型号分别为NACA1412、NACA4412、NACA6412。两组翼型的几何参数分别见表1、表2，图2为不同翼型的几何示意图。

表1 对称翼型组翼型基本参数Tab.1 Parameter values of symmetric airfoil group mm

表2 非对称翼型组翼型基本参数Tab.2 Parameter values of asymmetric airfoil group mm

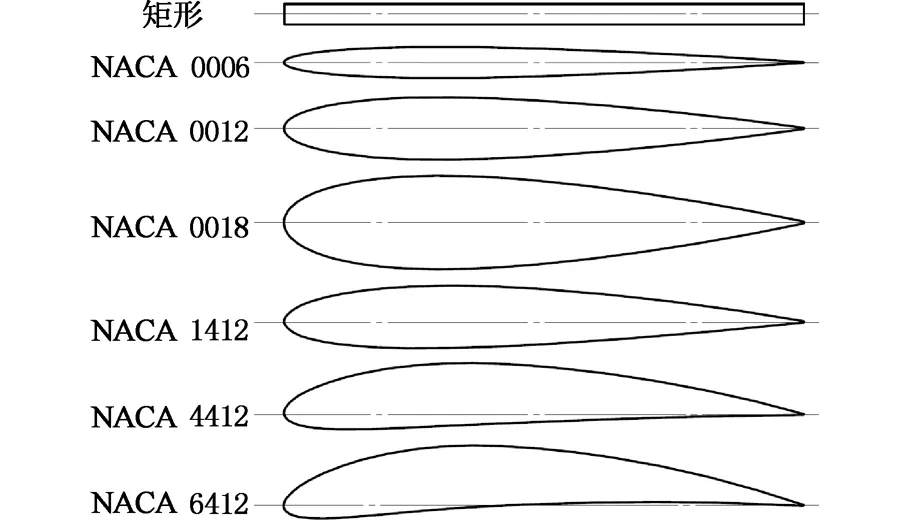
图2 不同型号翼型示意图Fig.2 Diagram for different types of airfoils

2 数值计算方法

2.1 几何模型及计算域

“海燕”混合驱动水下滑翔机模型如图3所示，滑翔机主体外壳直径为0.22 m，机身长2.3 m，机翼翼根前缘安装位置距离滑翔机头部顶点1580 mm，翼展为1.01 m，前缘后掠角为50°，后缘后掠角为45°，机翼整体形状为梯形，其中，翼尖弦长为117.65 mm，翼根弦长为226.59 mm。滑翔机采用滑翔方式实现低速、长距离运动，而在螺旋桨驱动模式下完成短期定深、快速航行以及转向等动作。

图3 “海燕”混合驱动水下滑翔机模型Fig.3 Geometric model of Petrel hybrid-driven underwater glider

计算域整体为圆柱体，如图4所示，水域直径尺寸为10 m，计算域轴线与滑翔机壳体轴线重合。水流入口边界设置于距离滑翔机头部4倍体长处，入口边界条件为速度入口；水流出口边界设置于距离滑翔机尾部5倍体长处，出口边界条件为自由流出；滑翔机所有壁面均设定为静止无滑移壁面，壁面粗糙度为0；池壁边界为圆柱面，设为对称边界[17]。

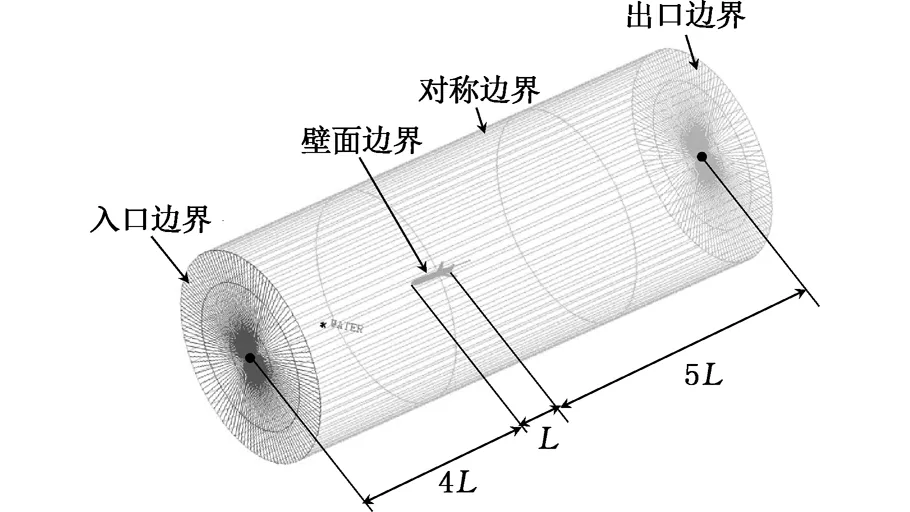
图4 计算域及边界条件Fig.4 Computational geometric field and boundary condition

2.2 网格划分

网格划分时采用尺寸函数与非结构化网格的方法相结合，这样既可以保证整体网格疏密的合理分布，又可以使网格的生成方法简单方便。对滑翔机机体面网格进行加密处理，机体表面最大网格为10 mm，机翼部分最大网格为6 mm，其余表面最大网格为4 mm。滑翔机外表面附加边界层，初始网格高度为0.77 mm，网格增长率为1.15，共6层边界层。滑翔机机翼部分网格划分如图5所示，附近边界层网格如图6所示。

图5 机翼部分网格划分Fig.5 Grids in the wing

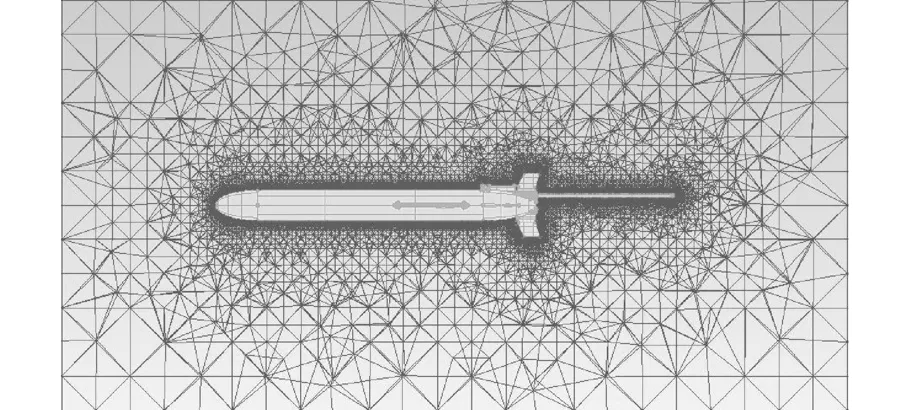
图6 滑翔机附近水域网格划分示意图Fig.6 Grids in the water field around glider

2.3 计算模型及求解

对于当前研究对象的水下滑翔机，滑翔模式下的雷诺数约1.16×106，因此，采用湍流模型对所建水域进行模拟。模拟时假定流体为不可压缩连续性介质，控制方程组为描述牛顿流体的连续方程及N-S方程[18]，湍流方程采用SST k-ω模型，求解方法选用“simplic”，二阶迎风模式，流体密度(海水密度)ρ=1025kg/m3，黏度μ=0.00 107kg/(m·s)。

计算过程中滑翔机主体尺寸及机翼布局不变，只改变机翼的翼型，滑翔机航速为0.5m/s，攻角α分别取 0°、±2°、±4°、±6°，其中，正攻角对应于水下滑翔机下潜滑翔状态，负攻角对应于水下滑翔机上浮滑翔状态。

2.4 模型的验证

为了验证所建数值模型的准确性，按照上述建模方法对Slocum滑翔机[19]在不同攻角下的阻力系数进行计算，并与文献[13]中的海试试验数据进行比对，数据对比结果见表3。可见，计算结果与试验结果相近，误差不超过11%，说明本文数值计算方法可靠。

表3 Slocum阻力系数Cd数值模拟结果验证Tab.3 Validation of the drag coefficient obtained from numerical simulation for Slocum glider

3 分析指标

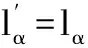
(1)

lα=-Mα/Lα

(2)

4 结果与讨论

4.1 对称翼型组

图7所示为对称翼型组升阻比的模拟试验结果。从图7可知，具有对称翼型的水下滑翔机在零攻角时升阻比最小(即滑翔经济性最差)，几乎为零；在正攻角和负攻角范围内航行时，其升阻比变化趋势大体相同，即随着攻角绝对值的增大，升阻比也增大。翼型厚度对滑翔经济性有一定影响，具有较厚翼型模型(如NACA 0018)的升阻比相较具有较薄翼型模型(如矩形翼型、NACA 0006、NACA 0012)的升阻比有较大降低，即机翼越厚,越不利于水下滑翔机滑翔经济性的提升。在-4°≤α≤+4°范围内，较薄的矩形翼型、NACA 0006、NACA 0012这三种对称翼型之间的升阻比相差不大；但随着攻角的继续增大，如攻角为±6°时，NACA 0006和NACA 0012翼型的升阻比会有较大提升，相比于矩形翼型，经济性有所提高。综上所述，在选择对称翼型的机翼时，可选较薄的NACA 0006翼型、NACA 0012翼型和矩形翼型，以提高滑翔经济性。

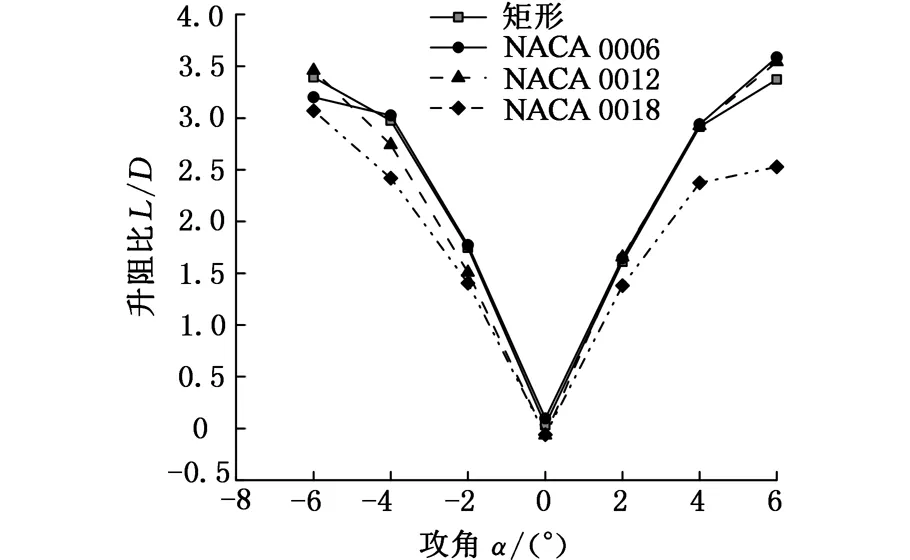
图7 对称翼型组经济性结果Fig.7 Flight efficiencies of symmetric airfoils group

图8所示为对称翼型组稳定性模拟试验结果。由图8可知，四种翼型的滑翔机均可保持静稳定；但随着翼型最大厚度的增大，滑翔机的静稳定性有所降低。

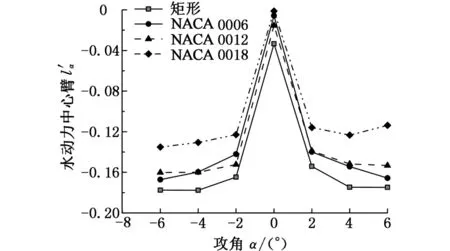
图8 对称翼型组稳定性结果Fig.8 Static stabilities of symmetric airfoils group

4.2 非对称翼型组

图9所示为机翼最大厚度相同的非对称翼型组(如NACA 1412、NACA 4412、NACA 6412)与对称翼型(如NACA 0012)升阻比的模拟试验结果。由图9可知，具有非对称翼型的水下滑翔机升阻比在正攻角(下潜滑翔状态)范围内随着翼型弯度的增加而增大，所有非对称翼的升阻比均高于对称翼型的升阻比；在负攻角(上浮滑翔状态)范围内的变化则正好相反。这说明了非对称翼型与对称翼型在提高滑翔机经济性上的差别，在正攻角范围内，非对称翼型可以提供更高的升阻比；即在下潜滑翔时，具有下弯状态的非对称翼型的水下滑翔机具有更好的滑翔经济性，弯度越大，滑翔经济性越好。而在负攻角范围内，非对称翼型的经济性比对称翼型的经济性差。

图9 非对称翼型组经济性结果Fig.9 Flight efficiencies of asymmetric airfoils group

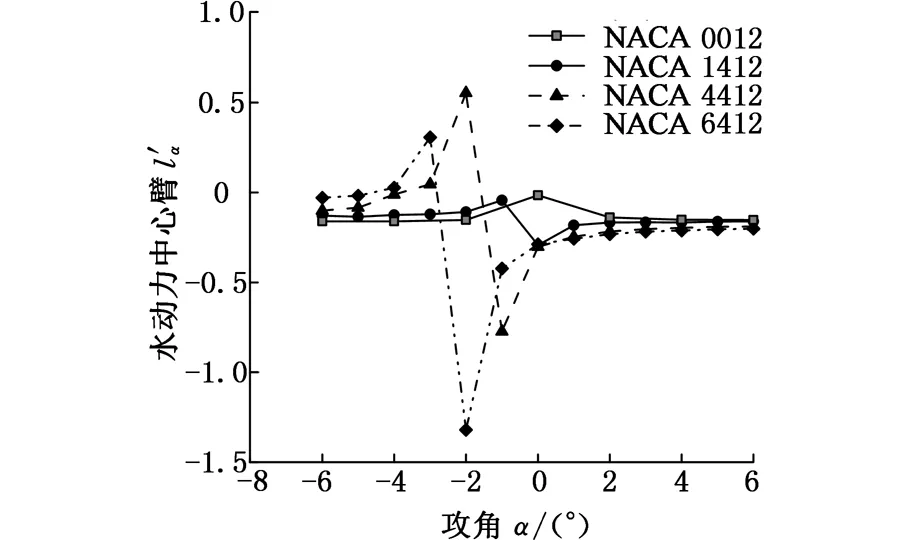
图10 非对称翼型组稳定性结果Fig.10 Static stabilities of asymmetric airfoils group

所以，当采用下弯式非对称翼型时，应尽量使滑翔机保持在正攻角范围内航行；相反，若采用上弯式非对称翼型，则应使滑翔机保持在负攻角范围内航行。

5 变后缘柔性机翼

5.1 柔性机翼概念的提出

针对本文研究对象“海燕”混合驱动水下滑翔机，多次海试试验后发现：①由于机翼初始外形设计均为刚性固定翼，只能适应特定的滑翔速度，导致水下滑翔机在高速滑翔(螺旋桨开启状态)时容易失稳；②大翼展机翼的存在，使水下滑翔机在定深航行中阻力系数增大，如图11所示，进而使滑翔机阻力升高，极大地降低了续航能力。根据4.2节的分析发现，合适的非对称翼型有利于提高水下滑翔机的滑翔经济性。因此，如果将水下滑翔机的机翼设计成能随不同运动模式自动改变其水动外形的柔性机翼，对于提高水下滑翔机的运动性能及续航能力具有重要意义。

图11 有翼与无翼滑翔机定深航行时的阻力系数对比Fig.11 Comparison of drag coefficients between fixed-wing glider and no-wing glider in depth-keeping flight

由4.2节的分析可知，为获得最佳航行性能，水下滑翔机不同运动模式下需要的翼型实际上也有所不同，如下潜滑翔时，翼型向下弯曲有助于获得较大的升阻比。但是工程上很难实现整个翼型的精确变形。通过观察不同类型的翼型可发现，非对称翼型相对于对称翼型，可类比为机翼后缘的向下弯曲变化形式。由此推测，在不同的攻角下，机翼翼型后缘的弯折变化同样会对水下滑翔机的经济性和稳定性带来类似的影响。为此，本文提出软体柔性机翼概念，如图12所示，为提高滑翔经济性，当水下滑翔机下潜滑翔时，机翼后缘变为下弯形状；当上浮滑翔时，机翼后缘则变为上弯形状；定深航行时，机翼可收回，以减小航行阻力。

图12 不同航行模式下机翼翼型概念示意图Fig.12 Concept sketches of changeable airfoil in different flight modes

本文采用数值模拟试验的方法研究软体柔性机翼的初步变形方案，后续研究中将重点解决软体柔性机翼的设计与实现。

5.2 变后缘机翼数值模拟试验

为了研究机翼后缘弯度变化对水下滑翔机经济性的影响，以矩形平板翼为研究对象，通过改变机翼后缘弯折角度来研究机翼后缘变化对水下滑翔机滑翔性能的影响。研究方案如下：在矩形翼型的85%弦长处分别将后缘弯折±6°、±15°、±30°，得到各变后缘翼型，如图13所示，本次模拟试验中攻角α分别取0°、±2°、±3°、±4°、±5°、±6°。

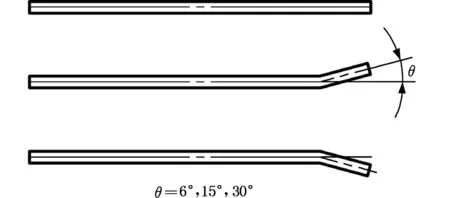
图13 变后缘翼型示意图Fig.13 Diagram of airfoil with changeable trailing edge

5.3 结果与分析

经过相同的数值计算过程后，得到升阻比计算结果如图14所示。从图14a可以看出，在机翼后缘上弯时，在负攻角范围内具有较高的升阻比，上弯的角度越大，升阻比越高；但是当攻角α≤-4°后，升阻比增大不再明显，各模型的升阻比趋于相同。而在机翼后缘下弯时，如图14b所示，在正攻角范围内具有较高的升阻比，下弯的角度越大，升阻比越高；同理，当攻角α≥4°后，升阻比增大不再明显，各模型的升阻比趋于相同。此计算结果与非对称翼型的计算结果相似：机翼后缘的下弯角度增大，对于非对称翼型则是最大弯度的增大，其升阻比在正攻角范围内随之增大。变后缘组的试验结果也证明了非对称翼型组计算结果的正确性。

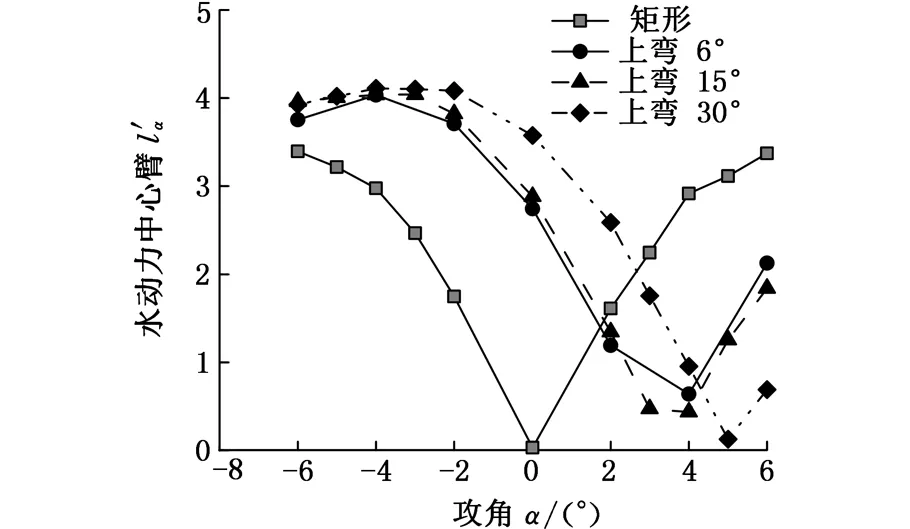
(a)后缘上弯

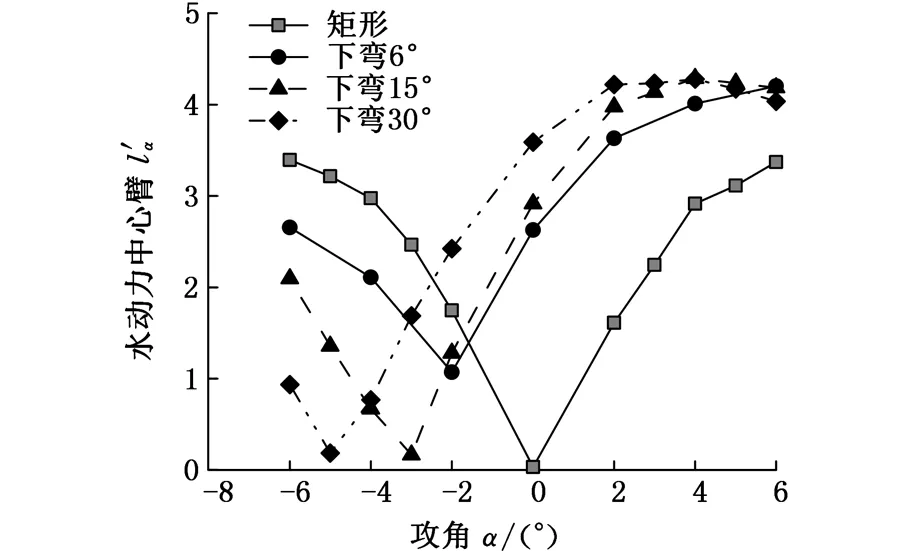
(b)后缘下弯图14 机翼后缘弯曲状态不同时水下滑翔机的升阻比随攻角变化Fig.14 Variation of lift-drag ratio with attack angles under different warping trailing edge

由以上试验数据的分析可知，若水下滑翔机在正攻角范围内航行时机翼后缘下弯，则可提高滑翔经济性；在负攻角范围内航行时，机翼后缘上弯，可以提供较好的滑翔经济性；-4°≤α≤4°时，后缘下弯的角度越大，可以提供的经济性越好，但是当攻角的绝对值超过4°以后，后缘弯曲角度的大小对滑翔经济性的影响不再明显。所以滑翔机在水下航行时，可以根据航行攻角适当改变机翼后缘弯度，以实现航行收益最大。

从机翼流场压力分布情况可进一步理解机翼后缘变化对水下滑翔机滑翔经济性的影响。图15和图16分别为α=4° 和α=-4° 时距离滑翔机对称面200 mm处机翼周围流场压力云图。由图15可以看出，α=4°时，后缘下弯的机翼(图15b)上下表面产生了较大的压差，有利于提高滑翔机的升力，进而提高滑翔经济性；反之，后缘上弯的机翼(图15a)在前缘和弯折处产生了相反的压差，形成了一组力矩，对滑翔机的升力起到了反作用，进而减小了升阻比，所以此时的滑翔机经济性较差。而α=-4°时(图16)，则与上述情况相反，此时后缘向上弯折更有利于提升滑翔经济性。

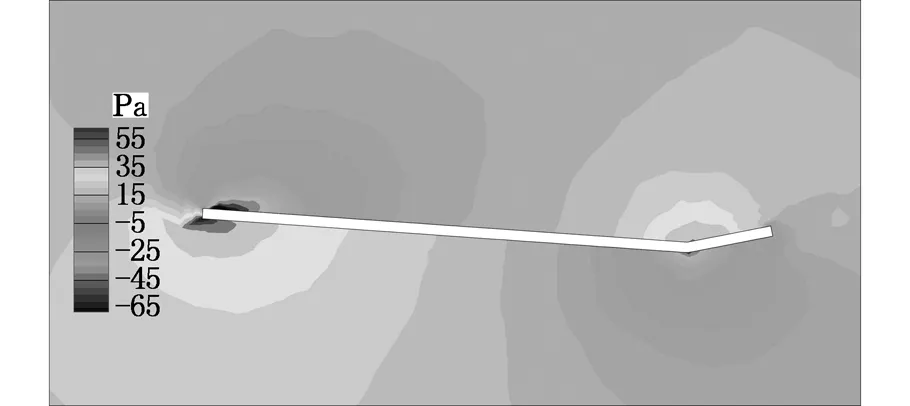
(a) 后缘上弯

(b)后缘下弯图15 α=4°时后缘弯折15°机翼截面压力云图Fig.15 Pressure contour in the flow field around the wing with 15° warping trailing edge under 4° angle of attack

(a) 后缘上弯

(b)后缘下弯图16 α=-4°时后缘弯折15°机翼截面压力图 Fig.16 Pressure contour in the flow field around the wing with 15° warping trailing edge under -4° angle of attack

机翼变后缘组的稳定性计算结果如图17所示。可以看出，后缘变化方向不同，在正负攻角范围内的稳定性也不同：机翼后缘下弯时，在正攻角范围内可保持静稳定性；机翼后缘上弯时，在负攻角范围内可保持静稳定性。同时，后缘下弯组在负攻角范围航行时会出现失稳现象，而且弯折的角度不同，出现失稳情况时对应的攻角也不同。这与非对称翼型组的稳定性变化情况相同。后缘上弯组的稳定性变化情况与下弯组相反。

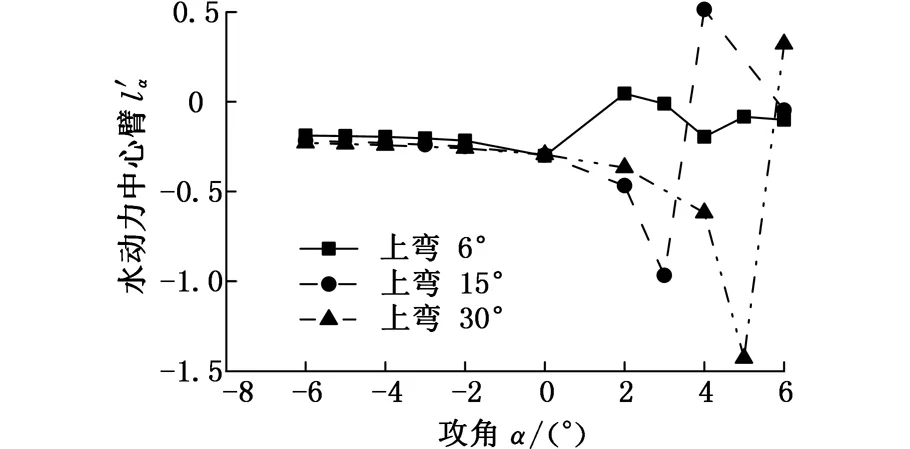
(a) 后缘上弯

(b)后缘下弯图17 机翼变后缘组稳定性结果Fig.17 Static stabilities of changeable trailing edge group

6 结论

(1)对于对称翼型，NACA 0006和NACA 0012翼型较现有翼型可以提供更高的升阻比，即提高滑翔状态下的经济性；翼型的变化对滑翔机的稳定性影响较小。

(2)对于非对称翼型，翼型的弯度发生了变化，并且在正攻角范围内提高了滑翔经济性。从试验数据中可以看出，随着翼型弯度的增大，滑翔机在正攻角范围内的升阻比也随之增大。

(3)水下滑翔机在负攻角范围内航行时，机翼后缘上弯，机翼周围流场会产生向下的压力差，提高了滑翔经济性，有利于滑翔机的上浮滑翔；反之，在正攻角范围内航行时，机翼后缘下弯可以提供较好的滑翔经济性，有利于滑翔机下潜滑翔。机翼后缘的变化也会影响滑翔机的静稳定性：后缘上弯时，滑翔机在负攻角范围内稳定性好；而机翼后缘下弯时，滑翔机在正攻角范围内稳定性好。

(4)本文研究成果为后续软体柔性机翼的变形方案提供了理论支持，可根据不同滑翔状态改变机翼后缘弯折方向，如滑翔机上浮则机翼后缘上弯，下潜则机翼后缘下弯，以提高滑翔机的滑翔经济性。

[1] Eriksen C C. Autonomous Underwater Gliders [R]. Sea Lodge:La Jolla, CA, 2003.

[2] JENKINS S A, HUMPHREYS D E, SHERMAN J, et al. Underwater Glider System Study[R]. USA：Office of Naval Research, 2003：2-21.

[3] 庞重光, 连喜虎, 俞建成. 水下滑翔机的海洋应用[J]. 海洋科学, 2014, 38(4)：96-100. PANG Chongguang, LIAN Xihu, YU Jiancheng. Ocean Application of the Underwater Glider[J]. Marine Sciences, 2014, 38(4): 96-100.

[4] 武建国, 陈超英, 王树新. 混合驱动水下滑翔器滑翔状态机翼水动力特性[J]. 天津大学学报, 2010, 43(1)： 84-89. WU Jianguo, CHEN Chaoying, WANG Shuxin. Hydrodynamic Characteristics of the Wings of Hybrid-driven Underwater Glider in Glide Mode[J]. Journal of Tianjin University, 2010, 43(1): 84-89.

[5] 赵宝强. 水下滑翔机水平固定翼设计[J]. 舰船科学技术, 2016, 38 (1)：103-107. ZHAO Baoqiang. The Horizontal Fixed Wing Design of Underwater Glider[J]. Ship Science and Technology, 2016, 38(1): 103-107.

[6] 宫宇龙, 马捷, 刘雁集. 实验尺度水下滑翔机的机翼设计与水动力分析[J]. 船舶工程, 2015, 37(8)：103-106. GONG Yulong, MA Jie, LIU Yanji. Flat Wing Design and Hydrodynamic Analysis Laboratory Underwater Glider[J]. Ship Engineering, 2015, 37(8): 103-106.

[7] ARIMA M, ICHIHASHI N, MIWA Y. Modelling and Motion Simulation of an Underwater Glider with Independently Controllable Main Wings[J].OCEANS 2009-EUROPE. IEEE, 2009: 1-6.

[8] ISA K, ARSHAD M R, ISHAK S. A Hybrid-driven Underwater Glider Model, Hydrodynamics Estimation, and an Analysis of the Motion Control[J].Ocean Engineering, 2014, 81(2): 111-129.

[9] FURLONG M E, PAXTON D, STEVENSON P, et al. Autosub Long Range: a Long Range Deep Diving AUV for Ocean Monitoring[C]//Autonomous Underwater Vehicles (AUV), 2012 IEEE/OES. IEEE, 2012: 1-7.

[10] YANG Zhijin, WANG Yanhui, WU Zhiliang, et al. Mechanism Design of Controllable Wings for Autonomous Underwater Gliders[C]//OCEANS’14 MTS/IEEE. Taipei, 2014: 1-5.

[11] 田文龙, 宋保维, 刘郑国. 可控翼混合驱动水下滑翔机运动性能研究[J]. 西北工业大学学报, 2013, 31(1): 122-127. TIAN Wenlong, SONG Baowei, LIU Zhengguo. Motion Characteristic Analysis of a Hybrid-driven Underwater Glider with Independently Controllable Wings[J]. Journal of Northwestern Polytechnical University, 2013, 31(1): 122-127.

[12] ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider: A Long-range Autonomous Underwater Vehicle for Oceanographic Research[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 424-436.

[13] GRAVER J G. Underwater Gliders: Dynamics, Control and Design[D]. Princeton：Princeton University, 2005：149-160.

[14] SHERMAN J, DAVIS R, OWENS W B, et al. The Autonomous Underwater Glider “Spray”[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 437-446.

[15] WANG Shuxin, SUN Xiujun, WANG Yanhui, et al. Dynamic Modeling and Motion Simulation for a Winged Hybrid-driven Underwater Glider[J]. China Ocean Engineering, 2011, 25(1): 97-112.

[16] SCOTT J.NACA Airfoil Series[DB/OL]. (2001-8-26)[2016-9-1].http://www.aerospaceweb.org/question/airfoils/q0041.shtml.

[17] 孙梦瑶.水下滑翔机粘性水动力数值模拟方法研究[D].天津；天津大学, 2014. SUN Mengyao. Numerical Simulation of Viscous Hydrodynamics of Unmanned Underwater Glider[D]. Tianjin:Tianjin University, 2005.

[18] TYAGI A, SEN D. Calculation of Transverse Hydrodynamic Coefficients Using Computational Fluid Dynamic Approach[J]. Ocean Engineering, 2006, 33(5/6)：798-809.

[19] ALVAREZ A. Redesigning the SLOCUM Glider Fortorpedo Tube Launching[J]. IEEE Journal of Oceanic Engineering, 2010, 35(5)：984-991.

[20] 马冬梅, 马峥, 张华. 水下滑翔机水动力性能分析及滑翔姿态优化研究[J]. 水动力学研究与进展(A辑), 2007, 22(6)：703-708. MA Dongmei, MA Zheng, ZHANG Hua, et al. Hydrodynamic Analysis and Optimization on the Gliding Attitude of the Underwater Glider[J]. Journal of Hydrodynamics(Ser. A), 2007,22(6):703-738.

[21] 施生达. 潜艇操纵性[M]. 北京：国防工业出版社, 1995. SHI Shengda. Submarine Maneuverability[M]. Beijing: National Defense Industry Press, 1995.

[22] WU Baoshan, XING Fu, KUANG Xiaofeng, et al. Investigation of Hydrodynamic Characteristics of Submarine Moving Close to the Sea Bottom with CFD Methods[J].Journal of Ship Mechanics, 2005, 9(3)：19-28.

(编辑 陈 勇)

Effects of Airfoil on Flight Performance of Autonomous Underwater Gliders

XU Shixun1,2LIU Yuhong1,2ZHU Yaqiang1,2WANG Yanhui1,2

1.Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin，300072 2.School of Mechanical Engineering，Tianjin University，Tianjin，300072

Based on the NACA 4-digit airfoil, effects of the airfoil on flight performance, such as flight efficiency and static stability, were analyzed by using the method of computational fluid dynamics with the environment of commercial software ANSYS-FLUENT. Results show that appropriate airfoil may greatly improve the flight efficiency of AUGs, but the improvements to the static stability of the AUGs are not so obvious. For asymmetric airfoils, the camber and bending directions of the airfoil have great influences on both of flight efficiency and static stability. According to the present researches and combining with the engineering practices, the flexible wings with variable trailing edge were proposed to make the AUG get better flight performance, which was proved by the numerical simulation experiments. The present achievements provide theoretical guidance for the design of flexible wings of AUGs.

autonomous underwater glider(AUG); airfoil; flight efficiency; flight stability；flexible wings with variable trailing edge

2016-10-09

国家自然科学基金资助项目(51475319，51675372)

TH122

10.3969/j.issn.1004-132X.2017.03.006

徐世勋，男，1992年生。天津大学机械工程学院硕士研究生。主要研究方向为水下滑翔机柔性机翼。刘玉红(通信作者)，女，1971年生。天津大学机械工程学院副教授。E-mail: yuhong_liu@tju.edu.cn。朱亚强，男，1992年生。天津大学机械工程学院博士研究生。王延辉，男，1979年生。天津大学机械工程学院副教授。