旋转锯片空气动力学噪声特性计算与分析

田永军 段国林 夏晓光 张 萼

河北工业大学机械工程学院,天津，300130

旋转锯片空气动力学噪声特性计算与分析

田永军 段国林 夏晓光 张 萼

河北工业大学机械工程学院,天津，300130

为分析旋转刀具在气流作用下的声学特性，基于多场耦合计算方程建立了流场-结构-声场联合仿真模型，通过弹性体与流场的动力学计算得到了结构强迫振动响应，利用边界元法将振动响应信息作为声学边界，获取了锯片的声场辐射信息，噪声预估值与实测结果吻合良好。研究了锯片旋转过程中周围流场媒介的层流、湍流特性对锯片振动的影响规律；揭示了流-固耦合作用对声场时域、频域影响作用机制；确定了锯片空载噪声辐射的方向特性；分析了锯片尺寸结构对噪声的影响规律，为低噪声锯片的设计提供了参考依据。

锯片；多场耦合；振动；噪声；预估

0 引言

锯机噪声按工作过程可分为锯切噪声和空载噪声。其中，空载噪声决定了锯机噪声水平的下限，空气动力学噪声是空载噪声的重要组成部分。锯机空载时间占大部分的工作时间，约80%[1]。由于锯机启动后不能随意停止，故对锯片空载噪声进行预估并分析，明确噪声来源，通过合理手段控制空载噪声，对于缓解锯机的高噪声干扰具有重要意义。

锯片噪声辐射问题一直是锯切领域研究的重点和热点问题。BIES[2]基于噪声用实验研究了锯片的噪声源。文献[3]基于边界元法(boundary element method,BEM)得到了锯片的声压分布，文献[4]通过噪声理论获取了锯片的声学特征。上述研究为锯片空载噪声预测提供了多种方案，但是由于空载噪声辐射问题不仅涉及流、固、声等学科，还包含大量非线性因素，上述研究大多对锯片噪声的声学边界信息进行了大量的简化，没有考虑旋转锯片与空气间复杂的双向耦合关系及锯片瞬态时变非线性等因素，具有一定局限性。为此，本文建立了流体-结构-声场多物理场联合仿真模型，该模型对锯片在实际工作过程涉及的复杂载荷激励以及声学边界条件进行了综合考虑，既模拟了旋转锯片振动特性及其周围流场动态行为，又对锯片的气动噪声辐射水平进行了预估，为揭示锯片流固耦合特性及声学特性提供了方法。

1 多场耦合分析理论基础

1.1 流体-结构耦合分析

流场中，高速旋转钝体的周围气流会迫使结构变形产生振动，而结构的位移变化又影响气流，两相介质间的相互作用称为流固耦合(fluid-structure interaction,FSI)现象。FSI问题控制方程为[5]

(1)

式中，k为迭代时间步；Aff、Ass分别为气流、弹性体的系统矩阵；ΔXFZ(〗WTBX〗kf、Bf分别为流体待求解项和作用力(外部)；ΔXFZ(〗WTBX〗ks、Bs分别为固体结构的对应项；Asf、Afs为耦合矩阵。

FSI问题重要的目标是得到结构振动响应(声学边界信息)，式(1)求解方法有以下两种：①直接法。将方程放在一个矩阵组求解，精度高，但是由于耦合域中各相的刚度不同，与流场相连的数值矩阵和与结构相连的数值矩阵相差多个数量级，导致计算量巨大。②分区迭代法[6-7]。其本质如下：在每一个时间步长按顺序分别求解流体和固体控制方程，按规定通过流固交界面把流域网格与结构网格信息进行相互插值计算，可以准确快速地实现两相介质的计算结果交换传递。

1.2 结构-声场耦合分析

结构-声场耦合是结构振动与声学介质波动的相互作用而产生的声辐射问题。通常利用FEM/BEM[8]法求解耦合系统获得声辐射信息，原理是利用将流固耦合场(FEM)得到的振动信息作为声学边界传递给BEM网格，从而进行求解获得结构的声场特征。

结构-声系统耦合方程详见文献[4-5],声学辐射的求解还需满足Helmholtz方程[4-5,8]，若机械工作现场可近似视为三维半空间[9]，地面可视为刚性面边界处理，即法向振动速度为0，则Helmholtz方程中格林函数G[4-5]定义如下:

GH=G(rp,rq)+RHG(rp1,rq1)

(2)

其中，RH=1，rp1、rq1表示镜像点。由流场-结构控制方程(式(1))，联立结构-声方程以及声场积分方程耦合求解即可获取动态旋转系统全过程的声压、振动信息。

2 锯片多场耦合系统框架及模型

将锯片、夹盘、空气域组成一个整体系统并作为研究对象，该多场耦合系统求解流程框架及计算模型如图1、图2所示。

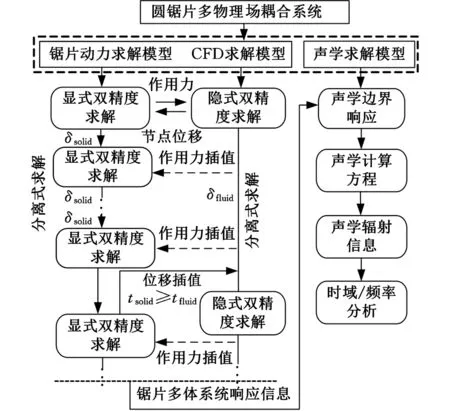
图1 多场耦合系统框架Fig.1 Flow chart of multi-field coupling system

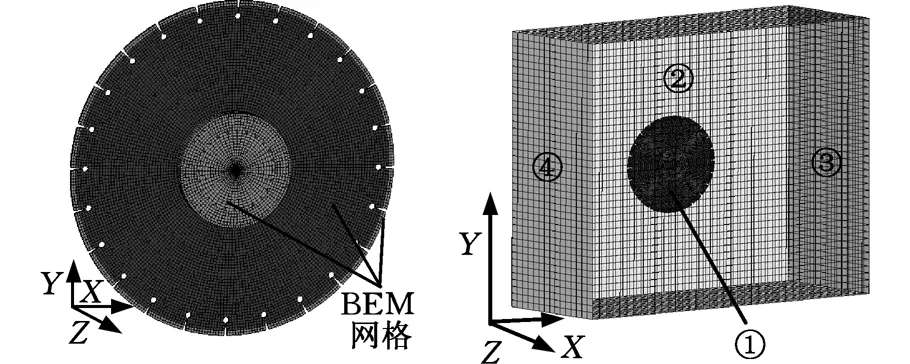
(a)FEM模型及BEM声学模型 (b)多物理场耦合模型及其边界①非滑动边界 ②流场自由滑动边界 ③流场入口流速 ④流场出口的压力图2 锯片旋转系统多物理场耦合计算模型Fig.2 Multi-physics coupling calculation model

2.1 锯片旋转系统多耦合场仿真流程

旋转锯片系统与空气媒介间刚度数值矩阵差距巨大，直接求解耦合方程计算量太大，因此，将锯片与气体间耦合方程进行解耦，采用效率更高的分区迭代法进行计算(图1)，对于空气流域子系统的流场特性分析，采用隐式双精度方程进行计算分析；对于锯片多体结构子系统的动力学分析，采用显式双精度计算方程进行求解，且两者之间是按顺序相互迭代求解的。图1中，δsolid、δfluid分别为锯片多体结构和气体的计算子步长，在计算初始时刻将流场作用力通过插值方式传递给刀具结构，当总步长tsolid≥tfluid时，结构位移信息通过耦合界面传递给气体网格，满足流固控制方程收敛条件后，经多次迭代获得旋转结构在耦合场响应信息。最后，将圆锯片及夹盘表面振动速度作为声学边界条件映射到边界元声学网格，通过求解声学波动方程即可获得锯片气动噪声辐射信息。

2.2 旋转锯片系统多耦合场计算模型

计算模型如图2a所示，几何参数如下：锯齿24个，夹盘直径为120 mm，锯片直径为350 mm，内孔直径为25.4 mm，基体厚度为2.5 mm。边界条件如下：锯片绕Z轴转动，转速为3000 r/min。如图2a所示，采用三维实体单元对旋转结构进行离散，初始时刻网格数目为26 840，FEM网格用于获取结构瞬时振动响应信息。声学响应则不能采用实体单元计算，只能采用二维网格计算，因此，本文在锯片实体单元表面提取降维的二维网格定义为BEM单元，网格数目为21 368。此时BEM、FEM间网格在对应位置的节点坐标重合，从而保证了振动响应信息映射声学边界时数据输入的准确性与同步性。

声学模型填充流体媒介后得到多场耦合模型，该模型可分为4部分(图2b)。流域体积为1.5 m×1.5 m×0.5 m。流域边界条件定义如下：①非滑动边界由旋转结构组成；②自由滑动边界由空气域组成；③初始时刻入口流速定义为0；④流场出口的压力定义为0，即没有外界风速干扰。FSI分析中，为了节省计算，大多数研究将计算域分为静网格和运动网格两部分。为了提高计算精度，实现各部件按真实规律运动，本文在流域中利用ALE动网格技术实现流场全域动网格运算，在计算过程中为了消除网格翻转等现象，使用ICFD_Control_Adapt_Size网格划分技术对过度扭曲的网格进行自适应划分。

3 多场耦合系统计算及分析

计算过程以ANSYS、LS_DYNA R700等计算平台，通过显式、隐式结合的方式提取了结构在耦合场的瞬时强迫响应，并通过FEM/BEM法结合声学方程得到了锯片气动声辐射信息。

3.1 材料基本参数

空气本构方程为ICFD_Mat，密度为1.28 kg/m3，锯片周围气流运动速度较小(Mr<0.3)，可视为不可压缩湍流且黏性系数为常量，因此，采用ICFD_Control_Turbulence控制的k-ε湍流方程模拟空气域流动特性，k为湍流脉动动能、ε为脉动动能耗散率，k-ε方程中湍流系数表达式为μt=ρCμ(k2/ε)，其中，Cμ=0.09。基体选用Plastic_Kinematic方程描述其应力、应变等力学行为；锯齿由金刚石和金属结合剂组成，采用Mat_Elastic本构模型描述其动力学行为；夹盘刚度大，旋转时变形很小，采用Mat_Rigid本构模型将其定义为刚体。各部分的材料参数见表1。

表1 圆锯片材料的基本参数Tab.1 Material parameters of circular saw

3.2 耦合场计算分析

图3为在稳定阶段锯片周围流场的XZ截面速度及Y方向压力云图。从图3a可以看出，锯齿节块周围气体流动速度较快，而锯片内径周围气流速度变化较小，主要原因是刀具旋转时，弧区锯齿持续拍打其周围空气质点，迫使质点不断波动，导致此处的空气流速加快。从图3b看到，远离锯片的第一、四截面压力梯度相对较小，从第二、三截面图可以看到，受到锯片的影响，锯齿边界层周围流场压力为负，且在旋转过程中该区域负压现象一直存在。受到旋转锯片影响，锯齿周围的速度梯度大，流场扰动强烈，从而产生非定长空气压力，不稳定气压会迫使锯片产生振动继而诱发噪声辐射。

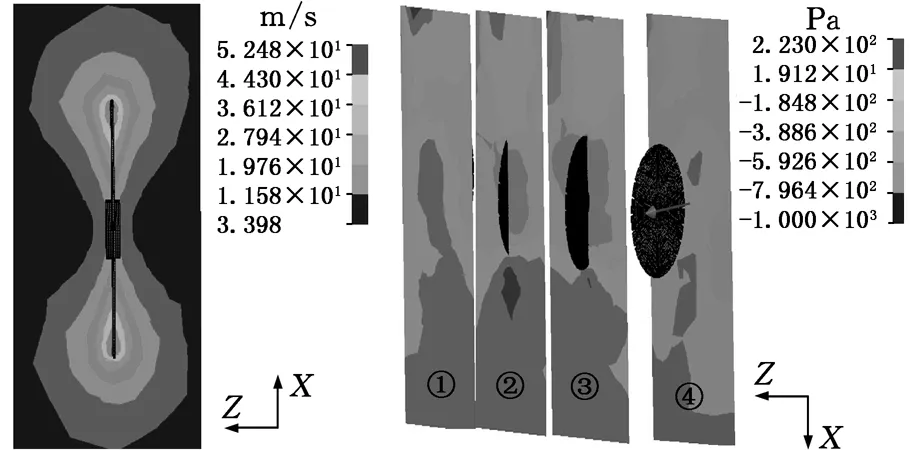
(a) XZ向流场速度云图 (b)Y向流场压力云图图3 0.10 s时锯片周围流场云图Fig.3 Flow pattern around the saw blade

图4所示为锯片周围空气流线图(XZ截面)，描述了锯片旋转过程周围流场变化情况。图4a中，在旋转初始阶段刀具上端周围气流较为稳定，而在刀具下端齿尖局部气流扰动不规则，出现湍流(turbulent flow)入射现象；图4b中，随转速增大，在锯齿周围湍流入射现象明显，而在其他区域没有明显的气流扰动，表明产生圆锯空气动力噪声的重要原因是锯片外悬伸出的不连续锯齿的作用导致气流流经此处产生分离而出现涡流现象；随后转速稳定，如图4c～图4d所示，湍流层区域扩大，在锯齿和锯片表面涡流分裂以及涡流脱落现象明显(偶极子源辐射现象)，这种周期性的脱落、分离作用导致锯片不断振动。由图4可以确定空载噪声产生的重要原因如下：旋转过程中锯片表面以及锯齿处形成的紊流与其接触并不断扰动，紊流经由锯齿被分隔为涡流并不断周期性地膨胀和压缩，促使空气流动复杂化(单双极子源耦合辐射现象)，同时锯片受到气流波动激励作用产生振动，进而产生噪声辐射。

(a)0.07 s时流场流线图 (b)0.08 s时流场流线图

(c)0.1 s时流场流线图 (d)0.13 s时流场流线图图4 锯片截面(Y=0)流场流线图Fig.4 Streamlines of saw’s cross section

4 模型验证

为验证模型的合理性，利用SERIES机床进行空载噪声实验，额定转速为3000 r/min，转差率在6%之内。大型车间测量噪声时，为减小声波反射对测量结果的影响，确定测量半径为1～1.5 m[10]，设备及测点布置如图5所示。

(a)实验设备图 (b)主视图及俯视图 1.振动监测点 2.采用激光测振仪OFV505提取横向振动速度 3.麦克风 4.LMS Test.lab为振动与噪声分析系统图5 实验设备以及噪声监测点Fig.5 Experimental equipment and monitoring points

4.1 噪声及振动的时域响应信息

锯片表面辐射噪声功率[4]可表示为

(3)

图6a给出了测量点(测点垂直于锯片，噪声测量半径为1m)空载旋转锯片声压级时域信息，在0～0.07s启动阶段实验中出现“啸声”现象，声压突然增大,随后在稳定阶段消失，数值分析中该现象表现不够明显，两组数据误差为5%～12%，实验值比仿真值大且声压波动平稳，主要原因是数值计算模型较理想化，尚未考虑锯机零部件振动以及其他因素的影响而导致声压较小，且在计算中出现流体动网格变形，使计算产生累计误差，导致在稳定阶段声压幅值波动大于实验数据。

图6b为锯片半径为0.8R及0.4R处锯片表面的横向振动信息。两测点振动幅值分别为-0.09～0.06 m/s和-0.03～0.03 m/s，仿真数据与实验数据吻合度较高，误差控制在6%～13%，对比数据得到以下结论：①离锯齿越近，锯片表面振动速度越剧烈，说明锯片噪声辐射源主要集中在锯齿周围；②离锯齿越近，振动幅度不对称性更加明显，主要原因是离锯齿越近，旋转过程锯片与空气间复杂激励导致锯片轴向刚度越不一致，而内部测点离夹盘较近，夹盘的预紧作用迫使其周围基体变形较小，从而使刚度变化小；③仿真中模型理想化，仿真数据振动幅度小于实验值，仿真过程流体网格变形造成累计误差等原因导致振动周期偏大。

(a)时域声压级曲线

(b)锯片表面测点横向振动速度曲线图6 测点的时域声压级及横向振动速度曲线Fig.6 Time domain sound pressure level and lateral vibration velocity curve of the measuring point

4.2 锯片辐射声场的噪声指向性

噪声指向性是指在相同的距离下，不同方向上声压的分布。依据图5测点布置，在相同条件下重复实验3次，获得各测点的声压平均值，如图7所示。分析可得以下结论：①以0°～180°线为基准，噪声分布呈对称趋势；②位于0°、180°测点处噪声最大，位于0°～90°、360°～270°、180°～270°、180°～90°处声压水平逐渐降低，主要原因是在垂直于锯片振动区域，锯片声辐射的有效面积最大，声场能量最高，随着角度的变化，有效辐射面积减少，声场能量也逐渐降低；③实验测量中(图5a)，由于90°～180°、180°～270°测点位于机器背面，机头等部件阻碍了噪声传播，以致噪声普遍小于270°～360°、0°～90°测点噪声；仿真结构建模对称，噪声沿X、Y方向分别呈对称趋势；④在一定范围内，随着距离增大，噪声呈衰减的趋势。空载噪声水平与实测相差5%～15%，表明模型具有一定的预测能力，同时噪声分析结果表明噪声辐射具有明显轴向对称性。

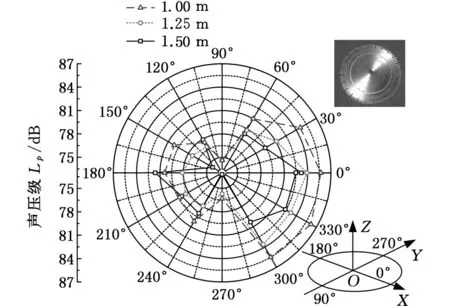
(a)空载实验

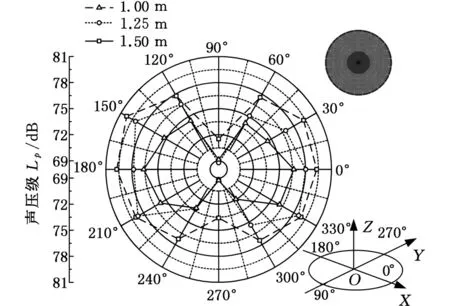
(b)空载仿真图7 噪声指向性Fig.7 Noise directivity

5 结果分析

5.1 流固耦合特性对气动噪声的影响

如图7所示，0°测点仿真值与实验值误差较小，因此，以该测点为例分析噪声声功率级随速度变化的情况。

由图8可知：①随转速增大，双向流固耦合条件与未考虑流固耦合条件的噪声预测值之间的差距逐渐增大，说明转速越大，FSI现象对噪声的影响越大。②锯片声功率与转速的4.3～4.8次方成正比，因此，气动噪声发射机理主要是单源和偶极子源两种声源的组合。这一结果与文献[11]提供的数值一致。若不考虑FSI现象中噪声声功率与转速的5.8～6次方成正比，即明显的双极子源特性，则与实际不符。③对比图7、图8，不考虑FSI现象时误差与实验值误差为10%～22%，在FSI效应下仿真与实验值误差为5%～14%。因此，噪声声压级水平的预估应尽量采用FSI算法。

图8 锯片声功率级随转速变化情况Fig.8 Sound power curve with speed changes

5.2 空载噪声频域分析

空载时，频谱分为两种：转频和齿通频率。由转速可得转频fs=50kHz，k=1,2,…。由转速及齿数得到齿通频率ftp=1200kHz，其中，k=1为基频，k=2,3,…为高次谐波频率。

图9为稳定阶段噪声频谱图，仿真值与实测数据的趋势走向吻合，但仿真模型简化，使得低频域段声压信息与实测值有较大误差。由频谱图发现声压集中在2200～3500 Hz，高频阶段比低频阶段的能量高，分析各频域段峰值与转频吻合良好，故认为转频是激发气动噪声的因素。实测高频噪声峰值集中在2690～2850 Hz附近，与齿通频率不对应，而在此区间内锯片的固有频率为2770.8 Hz，因此，可以推断出稳定阶段声压级主要是由锯片高阶固有频率激发的，即锯片激发的绕动力与锯片谐振或者固有频率同步激发锯片振动加剧，产生高频噪声。若在锯片表面或者内部增加阻尼材料，可改变锯片的固有特性，减小振动，可使高频噪声衰减。

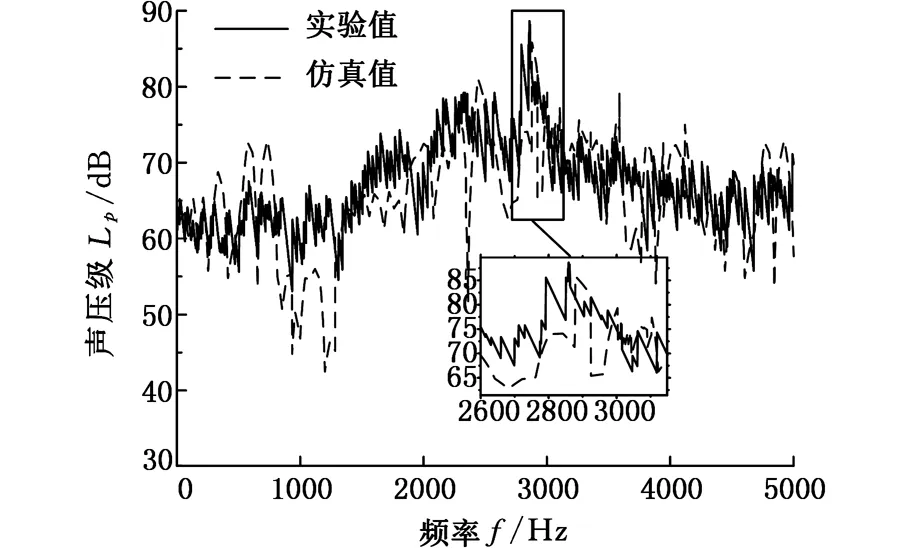
图9 旋转稳定阶段的噪声频域曲线Fig.9 Noise frequency domain curve of rotation stability stage

5.3 尺寸结构对锯片空载噪声的影响

通过改变锯片固有特性虽可抑制噪声源，但是采用黏性材料会大大增加工艺成本，而通过设计锯片尺寸结构使空气扰动激励降低以减小锯片振动与噪声更为合适。

就锯片而言，一定存在最佳结构使得气动噪声最小，本文将锯齿数量x1、基体厚度x2、锯片直径x3作为设计变量，考察锯片结构对气动噪声的影响。本文利用数理统计的响应面法结合自适应模拟退火法[12-14]对锯片尺寸结构进行分析并获取最优解。其步骤如下:在设计空间选取试验样本点，对样本点进行数值计算，获取声学、力学响应；然后利用最小二乘算法对响应值进行拟合，建立设计变量与响应目标之间的近似函数，即响应面模型；最后利用模拟退火法对响应面进行寻优，获取最优锯片最优尺寸结构。设计空间以及变量初始值见表2。

表2 设计变量以及设计空间

经过6次迭代计算，获取锯片尺寸与噪声之间的响应面数学模型。R2检验是评价模型精度重要指标[13]，经计算回归方程的检验值R2=0.928，说明近似拟合方程满足精度要求。获得回归方程后，对方程优化计算即可获取最佳点[13-14]。进行数据分析后，结论如下：①固定x1与x2，设计域内随着直径x3的增大，噪声呈现增大趋势，主要原因是夹盘尺寸固定，锯片直径的直径增大后夹紧比较小，则锯片旋转过程中波动幅度增大，直接导致噪声增大，当直径为470 mm时噪声有效值最大达89.2 dB，而当直径为261 mm时噪声有效值最小为75.9 dB。②固定x2与x3，在设计域内随着齿数x1的增大，噪声先增大后减小。主要原因是齿数增加导致齿间内气体涡流以及分离现象加剧，致使锯片表面非定常波动压力增大，从而导致噪声增大；当锯齿数目达到一定程度，锯齿总面积减小导致锯齿表面总压力减小和噪声降低，然而过多锯齿可能导致旋转过程中锯片应力增大以及刚度降低，从而导致转动不稳定。③固定x1与x3，在约束条件内随着锯片厚度x2的增大，噪声有增大趋势，锯片厚度对噪声影响较小，最大值与最小值相差为2.5～4.1dB。在保证刚度要求的条件下，经分析得到最优数值解如下：40.55齿(取整为40)、厚度为3.006 98mm、直径为261.21mm的锯片空载噪声最低。因此，可以设计锯片尺寸结构使空载噪声降低，锯片设计过程中各参数不是孤立的，最优尺寸设计是兼并上述参数的一个组合变量。

6 结论

(1)空载时锯片外边缘流场是复杂三维紊流，在旋转稳定阶段，锯齿顶端速度流通最大，流体压力变化也最大，而锯片外表面气流表现的湍流现象，表明锯齿及外边缘是空载噪声的主要噪声源，也是振动最为剧烈的区域。

(2)圆锯片旋转产生噪声辐射的重要原因如下：锯片表面以及锯齿处的形成的紊流与其接触并不断扰动，紊流经由锯齿被分隔为涡流并不断周期性地膨胀和压缩，促使空气流动复杂化，而锯片受到气流非线性激励作用而产生被迫振动，进而产生噪声辐射。

(3)对锯片空载噪声进行指向性分析后发现，气动噪声具有明显的轴向对称性，垂直于锯片方向气动噪声最大，平行于锯片两端噪声最小，同转速下两者相差达9dB。在一定范围内，随着距离的增大，噪声呈衰减的趋势。

(4)随锯片转速的增大，流固耦合作用对锯片空载噪声的影响更加明显。在频域上分析发现，旋转稳定阶段高频噪声主要是由锯片高阶固有频率激发的，表现在锯片表面激发的绕动力与锯片谐振或固有频率同步，迫使锯片振动加剧。

(5)在满足实际应用的条件下，减小锯片直径、适当增大锯片齿数、减小锯片厚度，可降低气动噪声。然而各参数不是孤立的，最优设计结构参数是一个权衡组合变量。

[1]LEUMC,MOTECD.OriginofIdlingNoiseinCircularSawsandItsSuppression[J].WoodScienceandTechnology, 1984, 18(1): 33-49.

[2]BIESDA.CircularSawAerodynamicNoise[J].JournalofSoundandVibration, 1992, 154(3): 495-513.

[3]YAOT,DUANG,WANGT.CoupledFEM/BEMMethodforNoisePredictionofCommonandSandwichCircularSawBlades[J].KeyEngineeringMaterials, 2016, 693:463-470.

[4] 肖杰.圆盘锯切噪声控制的研究[D].武汉:华中科技大学，2004.XIAOJie.OnCuttingNoiseControlofCircularSawBlade[D].Wuhan:HuazhongUniversityofScience&Technology，2004.

[5]RUGONYIS,BATHEKJ.OnFEAnalysisofFluidFlowsFullyCoupledwithStructuralInteractions[J].CMES-ComputerModelinginEngineeringandSciences, 2001, 2(2): 195-212.

[6]LÖHNERR,YANGC,CEBRALJ,etal.Fluid-structure-thermalInteractionUsingaLooseCouplingAlgorithmandAdaptiveUnstructuredGrids[C]//29thAIAAFluidDynamicsConference.Albuquerque,1998:1-16.

[7]DOSSANTOSN,GERBEAUJF,BOURGATJF.PartitionedFSIStrategyforSimulationsofaThinElasticValve[C]//ECCOMASCFDProceedings.Delft, 2006:3147-3170.

[8]SHARPER.ApredictionoftheAcousticalOutputofaGolfDriverHeadUsingFiniteElements[D].SanLuisObispo:CaliforniaPolytechnicStateUniversity, 2010.

[9]BAPATMS,SHENL,LIUYJ.AdaptiveFastMultipoleBEMfor3DHalf-spaceAcousticWaveProblems[J].EngineeringAnalysiswithBoundaryElements, 2009, 33(8): 1113-1123.

[10] 方丹群,张斌,孙家麟,等.噪声控制工程学[M]. 北京：科学出版社，2013.FANGDanqun,ZHANGBin,SUNJiaLin,etal.NoiseControlEngineering[M].Beijing:SciencePress,2013.

[11] 王厚立.试论圆锯的振动，噪音及减少噪音的途径[J].南京林业大学学报 (自然科学版) , 1983,4(2):20-38.WANGHouli.DiscussionontheVibration,NoiseandNoiseReductionofCircularSaw[J].JournalofNanjingForestryUniversity(NaturalScienceEdition), 1983, 4(2):20-38.

[12]POBLETEV,ARENASJP,RIOSR,etal.VibrationandIdlingNoiseinCommercialCircularSaws[C]//FifthInternationalCongressonSoundandVibration.Adelaide, 1997:1351-1358.

[13]STANDERN,ROUXW,EGGLESTONT,etal.ADesignOptimizationandProbabilisticAnalysisToolfortheEngineeringAnalyst[M].LSTC,Livermore, 2007.

[14]INGBERL.AdaptiveSimulatedAnnealing:LessonsLearned[J].ControlandCybernetics, 1996, 25(1): 33-54.

(编辑 陈 勇)

Calculations and Analyseis on Aerodynamic Noise Characteristics of Rotating Saw Blades

TIAN Yongjun DUAN Guolin XIA Xiaoguang ZHANG E

School of Mechanical Engineering, Hebei University of Technology, Tianjin,300130

In order to analyze the acoustic characteristics of the rotary tool under the fluid action, a combined simulation model was constructed based on coupled-field calculation equations. Firstly, the vibration response characteristics of the structure were extracted under the system which contained the rotating saw blades and air flow.Moreover, the vibration responses were regarded as acoustic boundary conditions to calculate acoustic radiation of the circular saw based on the boundary element method.Then, a structure acoustic coupling model was established to calculate the sound pressures. As compared with the experimental results, the coupling model may be used to noise prediction of the rotary tool.The laminar flow may turbulent flow characteristics of blade vibrations were studied in the processes of the rotating saw with around flow field and the sound radiation in time domain characteristics and laminar and turbulent characteristics with the coupled system was studied herein. Then,the characteristics of the directivity of aeroacoustic noise were studied. Finally，the influences of the size structure on the noise of the saw was determined, which provides a method for desining a low noise circular saw.

circular saw；multi field coupling；vibration；noise；prediction

2016-07-08

天津市自然科学基金重点资助项目(11JCZDJC23100)；河北省自然科学基金资助项目(F2014202241)

TP29;TH122;TB53DOI：10.3969/j.issn.1004-132X.2017.03.004

田永军，男，1988年生。河北工业大学机械工程学院博士研究生。主要研究方向为动力学优化设计、机械振动与噪声控制。段国林(通信作者)，男，1963年生。河北工业大学机械工程学院教授、博士研究生导师。E-mail：glduan@hebut.edu.cn。夏晓光，男，1988年生。河北工业大学机械工程学院博士研究生。张 萼，女，1989年生。河北工业大学机械工程学院硕士研究生。