基于试切误差补偿的斜齿插削技术与实验

吴震宇 赵大兴 钟瑞龄 许 万

1.湖北工业大学机械工程学院，武汉，4300682.宜昌长机科技有限责任公司技术中心，宜昌，443003

基于试切误差补偿的斜齿插削技术与实验

吴震宇1赵大兴1钟瑞龄2许 万1

1.湖北工业大学机械工程学院，武汉，4300682.宜昌长机科技有限责任公司技术中心，宜昌，443003

为了提高数控插齿机插削斜齿精度，提出了一种基于试切误差补偿的数控加工方法。首先，在分析斜齿螺旋线偏差产生机理的基础上，采用线段逼近理论主运动曲线，计算满足加工精度要求的线段最大许用步长和曲柄转角；然后，通过试切齿轮，测取螺旋线偏差并反求出主运动曲线偏差，获得更准确的新理论主运动曲线；最后，在生产用G代码中，重新用线段逼近新理论主运动曲线。实验结果表明：加工的斜齿轮螺旋线偏差达到7级精度，结果符合预期，验证了技术方案的可行性。

数控插齿机；电子螺旋导轨；螺旋线偏差；主运动

0 引言

斜齿加工精度和效率问题一直都是学术界和工业界的研究热点[1-5]，高性能的插齿装备加之合理的加工工艺，对提高斜齿加工精度和加工效率至关重要。插齿机加工斜齿轮时，斜齿螺旋线是靠螺旋导轨实现的，采用电子螺旋导轨技术的数控插齿机正逐步取代采用制造成本高、安装困难且通用性差的机械螺旋导轨技术的普通插齿机[6]，这为斜齿加工提供了相应的硬件保障，而开展高精、高效的斜齿插削技术及应用研究将对进一步提高斜齿加工质量提供技术保障。但即便是采用了电子螺旋导轨技术的数控插齿机，也不可避免地存在系统误差，因为其刀具旋转运动关系最复杂，由展成运动和附加转动组成[7]，如果刀具附加转动存在偏差，将直接产生螺旋线偏差；又因为电子螺旋导轨的刀具附加转动角位移是刀轴主运动线位移的函数，因此，由误差传递原理与等效分析原则可知，刀轴的主运动偏差将间接产生螺旋线偏差。目前国内插齿机的主轴大多采用曲柄连杆机构实现插齿刀的上下往复主运动[8]，这种主运动理论上应该是呈非线性的[9]，但是实际应用中，主运动曲线是由一系列线段按照一定的规律逼近理论主运动曲线[10]，不可避免地存在逼近偏差，因此，必然存在主运动偏差，从而导致螺旋线偏差的产生。为了解决由系统误差所引起的齿轮加工误差，国内外学者做了许多研究，归结起来主要集中在两个方面：①误差建模。早期只是建立了机床的几何误差模型，后来逐渐意识到温度场的影响是不可忽略的，进而考虑温度场影响，建立了机床热误差模型，试图从理论上寻找能够全面准确刻画机床误差产生机理的数学模型，进而从根源去规避误差的产生，但是这种方式不仅在建模上存在困难，而且在误差模型的适用性上存在局限性。②误差补偿。在这方面，大量的研究成果集中在坐标测量机上，相比之下，对数控机床误差补偿技术的研究进展缓慢，还处于探索阶段。本文基于先测出被加工件的误差，通过改变后续件的加工程序纠正加工误差的思路，设计了一种试切误差补偿的斜齿轮数控化插削技术方案，确立了插齿刀附加转动步长的计算和螺旋线偏差补偿的实现方法；通过插削加工实验，验证了该技术方案的可行性。

1 螺旋线偏差的产生机理

1.1 螺旋线偏差与主运动偏差关系

由斜齿成形理论可知，电子螺旋导轨附加转动与刀轴主运动必须满足下式：

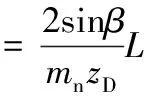
(1)

式中，θ为插齿刀附加转动角度；mn为插齿刀模数；zD为插齿刀齿数；β为插齿刀螺旋角。

由式(1)可知，当插齿刀的模数、齿数、螺旋角已知时，插齿刀附加转动角度θ与插齿刀在竖直方向上运动的距离L成固定比例，该比例称为附加转动系数，用K表示，即

(2)

由于工件齿轮转动偏差是由插齿刀附加转动偏差引起的，故工件齿轮螺旋线偏差e与插齿刀附加转动偏差θD之间的关系为

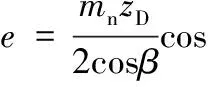
(3)

式中，αt为端面压力角。

通过式(1)可以由主运动曲线偏差得到插齿刀的附加转动偏差，通过式(3)可以由插齿刀的附加转动偏差得到工件齿轮的螺旋线偏差。所以主运动曲线偏差ΔL与螺旋线偏差e之间的关系为

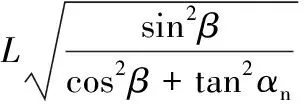
(4)

法面压力角αn恒等于20°，由式(4)可知，确定螺旋角β的值之后，主运动曲线的偏差将以固定的比例反映到工件齿轮的螺旋线偏差上。该比例系数称为Zebra系数，用Z表示，即

(5)

1.2 设计主运动偏差分析

对于目前多数刀轴主运动采用曲柄连杆机构的插齿机，其理论主运动曲线呈图 1所示的非线性。但是实际应用中，设计主运动曲线是由一系列逼近理论主运动曲线的线段构成的，因此，不可能保证与理论主运动曲线完全重合，导致必然存在主运动偏差。

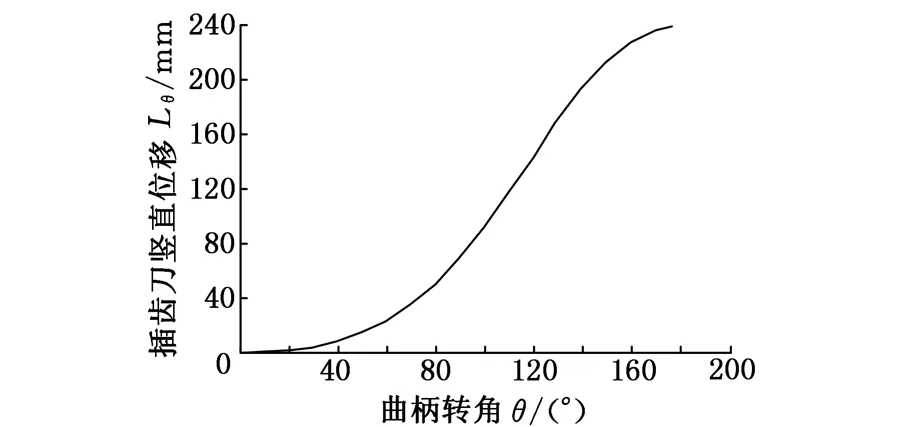
图1 曲柄连杆机构的理论主运动曲线Fig.1 Theoretical main drive curve of crank connecting rod

1.3 实际主运动偏差分析

笔者所在的课题组在对实际主运动曲线的分析研究中发现，受连杆长度及初始位置测量精度、运动副间隙、杆件受力变形及磨损等因素的影响，实际主运动曲线与理论主运动曲线存在不可忽略的差异，因此，也会产生主运动偏差[11]。

上述客观存在的设计主运动偏差和实际主运动偏差，使得螺旋线偏差的存在是不可避免的，但是能够通过采取合理的技术方案，将其降低在允许范围内。

2 试切误差补偿的插削技术方案

2.1 总体技术方案

针对1.2节的设计主运动偏差问题，本文按照任意位置的螺旋线偏差小于许用螺旋线总偏差的要求规划设计主运动曲线，计算满足齿轮加工精度要求的设计主运动曲线中线段的最大许用步长，限制曲柄每次转过的角度。

上述技术方案是针对设计主运动偏差的解决措施，但是由1.3节的分析可知，在多因素耦合影响下，存在不可忽略的实际主运动偏差，这部分影响的变化规律复杂且不确定。因此，本文在确定设计主运动曲线每段线段的最大许用步长和对应的曲柄转角的基础上，编制试切用的G代码，通过试切一次齿轮，测取螺旋线偏差，反求出主运动偏差；然后，将其补偿到理论主运动曲线中，由此获得更准确的新理论主运动曲线，重新按照任意位置的螺旋线偏差小于许用螺旋线总偏差的要求，用一系列线段逼近误差补偿后的新理论主运动曲线，得到重新规划后的设计主运动曲线；最后，根据新规划的设计主运动曲线，计算其每段直线的最大许用步长和对应的曲柄转角，编制生产用的G代码。

2.2 最大许用步长和对应的曲柄转角

本方案中，设计主运动曲线是采用一系列线段逼近理论主运动曲线得到的，因此，每段直线的最大许用步长和对应的曲柄转角直接决定螺旋线偏差能否控制在允许范围内。Max_Step代表最大许用步长，SP值代表设计主运动曲线中每段直线对应的曲柄转角。

图2中，[P]表示许用的主运动曲线偏差，由被加工齿轮的许用螺旋线总偏差得到，P1表示主运动曲线偏差线段中点的纵坐标值，P2表示与P1同横坐标的曲线上的点的纵坐标值，P表示P1与P2差值的绝对值。图3中，SP_All代表SP初始值，L_S代表上超越行程，L_Q代表上超越行程与切削行程的和，L_X代表总加工行程。

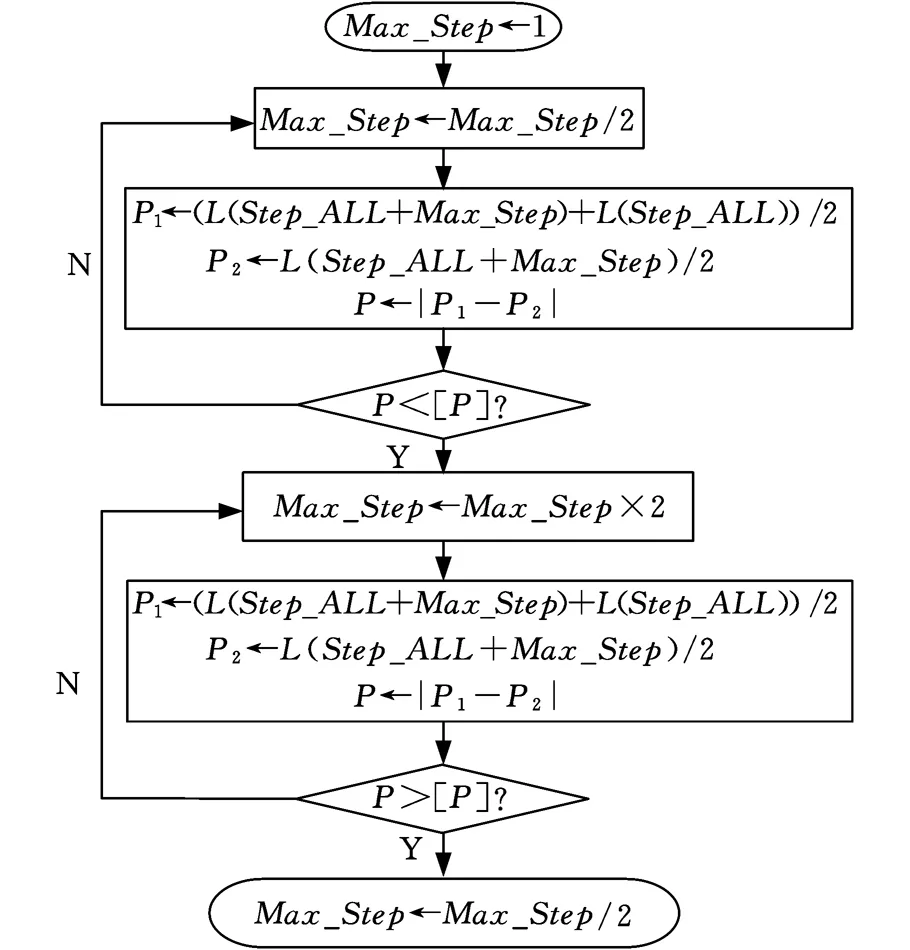
图2 最大许用步长的计算流程Fig.2 Calculation process of maximum allowable step

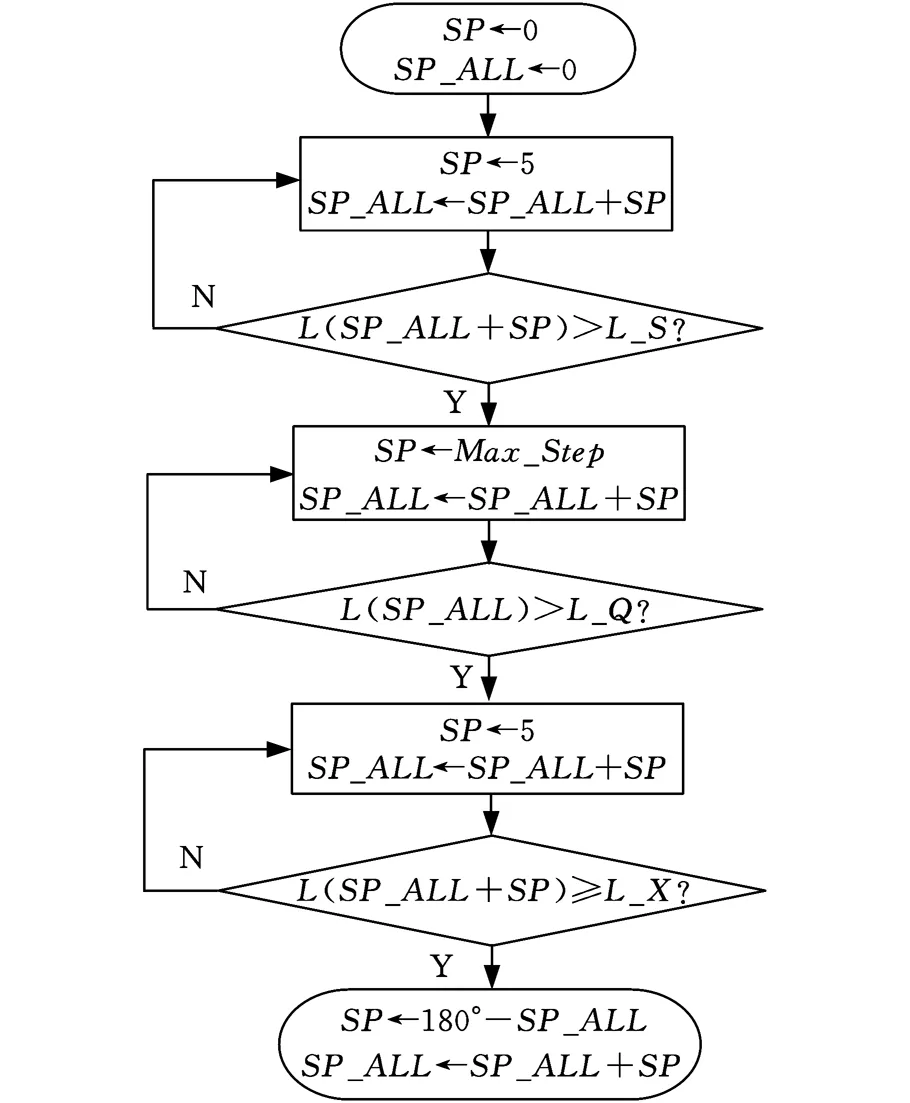
图3 曲柄转角的计算流程Fig.3 Calculation process of crank angle

3 螺旋线偏差的补偿

生产用G代码与试切用G代码的不同之处在于：前者根据试切齿轮螺旋线偏差检测结果，对后者切削行程部分代码进行螺旋线偏差补偿。螺旋线偏差的补偿是技术方案中必不可少的一环。整个补偿过程分为两部分：①减少上超越行程测量精度对补偿的影响；②沿齿宽方向对螺旋线偏差进行补偿，生成生产用G代码。

3.1 上超越行程测量精度的影响及处理

试切齿轮的螺旋线偏差结果反映沿齿宽方向任意位置处的螺旋线偏差。要将其补偿到G代码中，首先要确定螺旋线偏差补偿的初始位置，即上超越行程的实际大小。

图4为上超越行程测量精度影响示意图。粗实线表示实际上超越行程等于L_S时的螺旋线偏差检测结果。点划线表示实际上超越行程等于L_S_min时的螺旋线偏差检测结果。虚线表示实际上超越行程等于L_S_max时的螺旋线偏差检测结果。图4中的阴影线部分表示当实际上超越行程在L_S_max与L_S_min之间时，对应竖直位置必然存在的螺旋线偏差。显然，上超越行程测量精度越高，L_S_max-L_S_min就越小，必然存在的螺旋线偏差越接近检测结果。

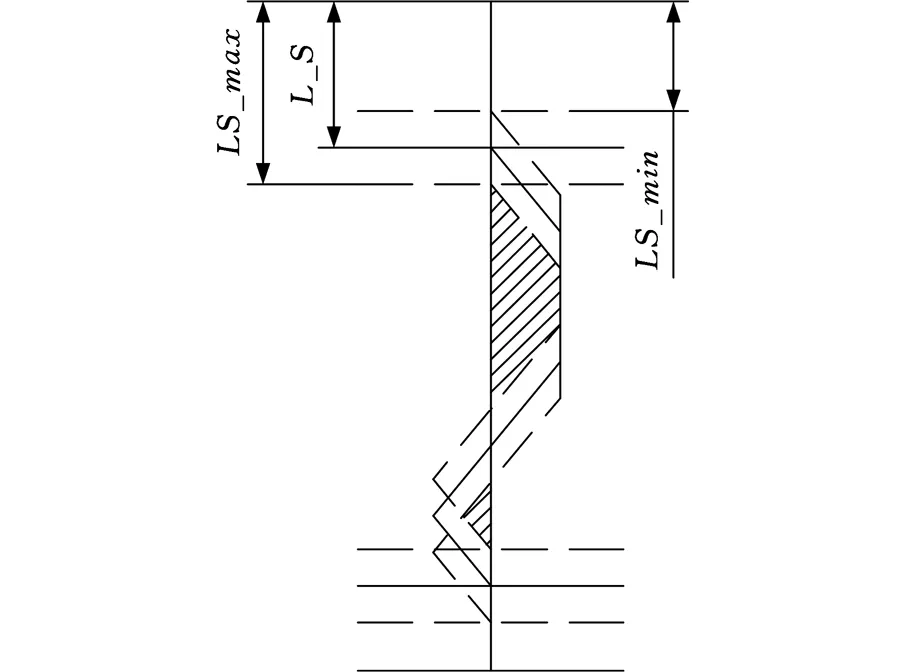
图4 上超越行程测量精度影响Fig.4 Influence of top-stroke precision

针对上超越行程测量精度带来的影响，如果只补偿必然存在的螺旋线偏差(即图4中阴影线部分，它是当上超越行程位于两个极限位置时，相对应的螺旋线偏差的“与”),这种方法必然导致部分螺旋线偏差没有得到补偿，甚至存在最大螺旋线偏差没有得到补偿的可能性。因此，本文采用降级法降低超越行程测量精度的影响，将螺旋线偏差检测结果所有值均乘以降级系数0.9，然后对新的螺旋线偏差进行补偿，即图 5所示阴影线部分。尽管理论上补偿完后仍然存在螺旋线偏差，但是，补偿之后的螺旋线偏差为补偿之前的0.1倍，即螺旋线偏差降低了一个数量级。尽管仍然存在部分螺旋线偏差没有得到补偿的可能性，但是它可以较好地减小上超越行程测量精度带来的影响，并且编程时更容易实现螺旋线偏差数据的输入、处理与保存。

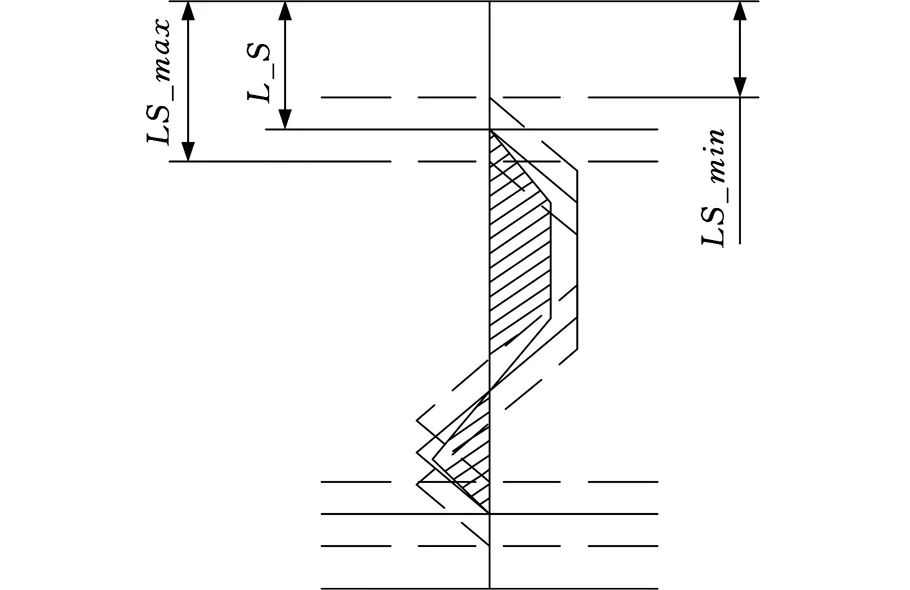
图5 降级法降低上超越行程测量精度影响Fig.5 Effect of degrading method on reducing the influence of top-stroke precision

3.2 螺旋线偏差补偿原理

由于分析研究中假设的加工条件与实际的加工条件之间必然存在差异，故实际检测中，试切齿轮各个齿面测量得到的螺旋线偏差会存在一定的差异，并且检测结果不会如图4、图5所示的那样简单、规范。针对该问题，本文采用的方法是先用线段去逼近螺旋线偏差，要求线段能体现各个齿面螺旋线偏差的变化趋势及各个极值点、转折点、零点；然后，按降级法对上超越行程测量精度的影响进行处理；最后，获得的螺旋线偏差再除以对应的Zebra系数，从而得到相应的主运动曲线偏差。

图6为螺旋线偏差补偿原理图。假设被加工齿轮为右旋斜齿外齿轮，则插齿刀应选择相应规格的左旋插齿刀。因此，进行附加旋转运动时，插齿刀逆时针旋转。假设测量的齿面为左齿面。用纵坐标表示主运动曲线偏差的位置，用横坐标表示主运动曲线偏差的数值，将主运动曲线偏差与主运动曲线表现在同一个坐标系中，如图6中的线段ab、bc。

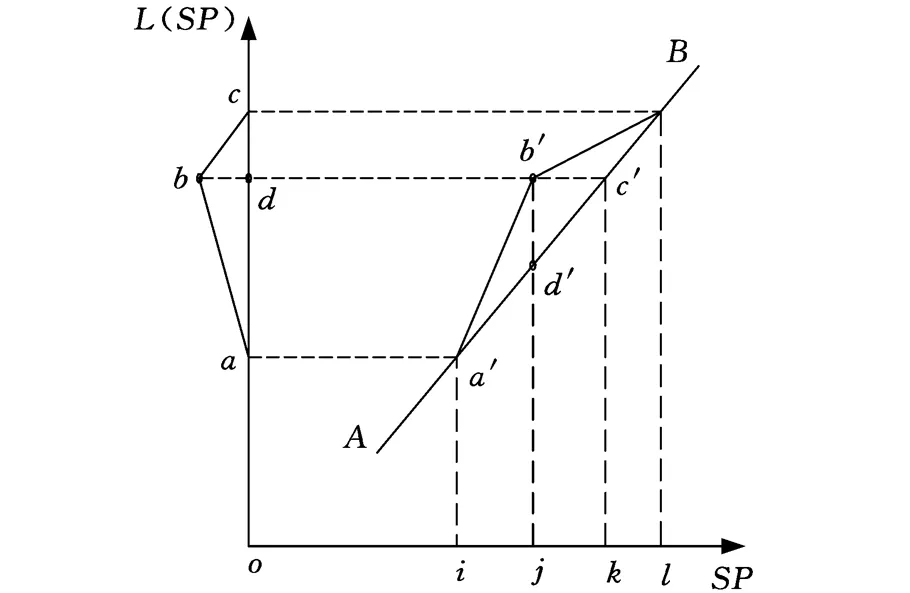
图6 螺旋线偏差补偿原理Fig.6 Compensation of helix deviation

图6中的线段AB为生成试切用G代码所用的设计主运动曲线中的一段。当SP在i～l之间时，插齿刀在竖直方向上的位置在L(i)～L(l)之间，此时存在主运动曲线偏差。当插齿刀实际位置位于L(k)时，主运动曲线偏差的绝对值达到最大值，即bd的长度。主运动曲线偏差为负，意味着螺旋线偏差为负，实际工件齿形比理论工件齿形少转了一定角度，实际插齿刀附加转动比理论插齿刀附加转动少了一定的角度。为了消除螺旋线偏差，与旧G代码相比，附加转动进行到该位置时，新的G代码必须控制插齿刀多转过指定角度，亦即新设计主运动曲线必须在旧设计主运动曲线之上。

假设bd的长度为Δ，新设计主运动曲线用L′(SP)表示。为消除当插齿刀实际位置位于L(k)时所对应的螺旋线偏差，要求当L′(x)=L(k)时,L′(x)-L(x)=Δ，即b′d′=bd。根据旧设计主运动曲线的斜率以及Δ的大小，可以求出x值，即图6中的j。根据新设计主运动曲线生成的G代码，当SP=j时，插齿刀的实际位置为L(k)，插齿刀比补偿之前多转了ΔK，其中，K为对应附加转动系数。同理，可对其他位置的主运动曲线偏差进行补偿。最终得到新的设计主运动曲线：Aa′、a′b′、b′c′、c′B。由新的设计主运动曲线生成生产用G代码。

4 切削加工实验

4.1 加工实验

为了验证技术方案的可行性，在宜昌长机科技有限责任公司的配合下，进行现场加工实验。在普通三轴数控插齿机床的基础上，将主轴电机由普通变频电机更改为伺服电机，同时更改数控系统的相关设置。所采用的加工参数如下：插齿刀齿数为69，工件齿数为91，模数为2.3091mm，螺旋角为27.5°，压力角为17.5°，工件齿宽为35mm，插齿刀左旋，工件右旋，工件材料为铸铁，刀具材料为高速钢。要求工件齿轮达到7级精度，许用螺旋线总偏差为18μm。共进行了三次加工实验，实验测量在SP-60 渐开线齿廓测量仪上进行。

第一次加工实验先用标准数控加工程序进行试切加工，使用的是试切用G代码，即螺旋线偏差补偿值为0，并用渐开线齿廓测量仪对被切齿轮进行齿廓测量。由于齿轮的螺旋线总偏差是方案成败的评判标准，故只进行螺旋线偏差检测。为了减少不必要的加工时间，加工出一定齿数之后便停止加工，选择中间的轮齿进行测量。后两次加工实验是螺旋线偏差补偿，得到的齿轮同第一次加工得到的齿轮外观相似。根据第一次加工实验得到的螺旋线偏差，选取两种补偿值方案，编制生产用G代码，载入数控系统中进行加工实验。由于补偿值不同，螺旋线偏差检测结果也不同。

4.2 实验结果分析

第一次加工实验螺旋线总偏差达到140μm，远大于许用值18μm。第二次加工实验时，用一线段表示要补偿的螺旋线偏差。即在专用程序中输入点(0,0)、点(35,140)。若技术方案及螺旋线偏差补偿算法正确，则补偿后的螺旋线总偏差应大大减小，并且螺旋线偏差曲线呈鼓形。在实际加工中，经过补偿之后的第二次加工实验的螺旋线偏差确实呈鼓形，螺旋线总偏差为30μm，较补偿之前的140μm小了很多，符合预期要求。但是第二次补偿之后的螺旋线总偏差仍然大于许用值。可以用梯形来表示第二次补偿之后的螺旋线总偏差，即点(0,0)、(10,30)、(24,30)、(35,0)确定的梯形。第三次加工实验时，用三段线段表示要补偿的螺旋线偏差，对第二次加工实验中没有补偿的部分也进行补偿。即在专用程序中输入点为(0,0)、(10,70)、(24,126)、(35,140)。若技术方案及螺旋线偏差补偿算法正确，则补偿后的螺旋线总偏差应小于许用偏差，并且螺旋线偏差曲线不会呈明显的倾斜。经过补偿之后的第三次加工实验的螺旋线总偏差为14μm，小于许用值18μm。相比第一次加工的检测结果，第三次加工实验的螺旋线偏差曲线并没有呈明显的倾斜。第三次加工实验成功地完成了螺旋线偏差补偿，补偿之后齿轮的螺旋线总偏差小于许用值，验证了技术方案的可行性及核心算法的正确性。

5 结论

(1)根据电子螺旋导轨插削斜齿成形理论，建立了刀具附加转动与刀轴主运动的运动关系，并推导出螺旋线偏差与主运动偏差的函数关系，从中发现螺旋线偏差是由刀轴主运动偏差所引起的。

(2)针对主运动为曲柄连杆机构的数控插齿机，分析了设计主运动偏差和实际主运动偏差的产生机理，从理论上论证了由直线逼近理论得到的设计主运动曲线与理论主运动曲线之间必然存在偏差，而且受到多因素耦合作用的影响，实际主运动偏差也是不可忽略的，变化规律非常复杂。

(3)按照任意位置的螺旋线偏差小于许用螺旋线总偏差的要求规划设计主运动曲线，确立了插齿刀转动步长的计算方法；分析了上超越行程测量精度对加工结果的影响，确立了螺旋线偏差补偿的实现方法。

[1]ZHANGYu,YANHongzhi.NewMethodologyforDeterminingBasicMachineSettingsofSpiralBevelandHypoidGearsManufacturedbyDuplexHelicalMethod[J].MechanismandMachineTheory,2016, 100:283-295.

[2]WUYR,TRANVT.TransmissionandLoadAnalysisforaCrownedHelicalGearPairwithTwist-FreeToothFlanksGeneratedbyAnExternalGearHoningMachine[J].MechanismandMachineTheory,2016,98:36-47.

[3]LOPATINBA,PLOTNIKOVASV,KHAUSTOVSA.InvoluteHelical-bevelGearing[J].ProcediaEngineering, 2015,129:891-895.

[4]JIANGJinke,FANGZongde.High-orderToothFlankCorrectionforaHelicalGearonaSix-axisCNCHobMachine[J].MechanismandMachineTheory, 2015,9:227-237.

[5] 丁国龙，张颂，赵大兴，等.齿轮成形磨削砂轮廓形优化研究[J].中国机械工程，2015,26(6)：743-748.DINGGuolong,ZHANGSong,ZHAODaxing,etal.OptimizationofGrindingWheelProfileforGearFormGrinding[J].ChinaMechanicalEngineering, 2015,26(6)：743-748.

[6]UENOK.NewGuidelessCNCShaperforHelicalGears[J].GearTechnology,1998,15(2):17-19.

[7] 朱玉.斜齿轮数控插削加工的运动分析和仿真[J].机械传动,2008,32(5):69-72.ZHUYu.KinematicsAnalysisandSimulationofNCShapingofHelicalGear[J].JournalofMechanicalTransmission,2008,32(5):69-72.

[8] 程伟林.具有急回特性的数控插齿机主运动系统的设计与控制研究[D].株洲：湖南工业大学，2015.CHENGWeilin.DesignandControlResearchfortheMainDriveSystemoftheCNCGearShapingMachinewithQuickReturnCharacteristics[D].Zhuzhou:HunanUniversityofTechnology, 2015.

[9] 魏兵，杨文堤.机械设计基础[M].武汉：华中科技大学出版社，2011. WEI Bing,YANG Wendi.Mechanical Design[M].Wuhan: Huazhong University of Science & Technology Press,2011.

[10] HE Jihua. Modeling and Simulation of the Mechatronic System of a Large and Heavy Duty CNC Gear Shaper[C]// 2010 International Conference on Digital Manufacturing and Automation(ICDMA 2010). Changsha, 2010: 956-959.

[11] 吴震宇,赵大兴,钟瑞龄.多因素影响的电子螺旋导轨误差的理论分析[J].中国机械工程，2016, 27(24)：3301-3306. WU Zhenyu, ZHAO Daxing, ZHONG Ruiling. Theoretical Analyses on Errors of Electronic Helical Guides Influenced by Multi-factor[J].China Mechanical Engineering,2016,27(24):3301-3306.

(编辑 陈 勇)

Helical Gear Shaping Technology Based on Error Compensation by Trial Cuts and Experiments

WU Zhenyu1ZHAO Daxing1ZHONG Ruiling2XU Wan1

1.School of Mechanical Engineering, Hubei University of Technology, Wuhan, 430068 2.Technology Center, Yichang Changji Machine Technology Co., Ltd., Yichang, Hubei, 443003

A machining technology based on error compensation by trial cuts was presented for improving machining precisions of a helical gear for CNC gear shaper. Firstly, the ideal main motion curve was derived using some straight lines approaching the ideal main motion curve, where the maximum allowable step of each straight lines and the corresponding crank angles that might satisfy the demands of machining precision were calculated. Then, the deviations of the main motion curve were calculated by the helix deviations of gear trial cuts, and a new more accuate ideal main motion curve was derived. At last, the new ideal main motion curve was approached by some straight lines again in the G codes used final gear machining. The test results show that the helix deviations of machined helical gears achieve 7 level accuracy, and satisfy the demands, and which verifies the feasibility of the method presented herein.

CNC gear shaper; electronic helical guide; helix deviation; main motion

2016-06-12

国家自然科学基金资助项目(51405144);国家科技重大专项(61375092)；湖北省重大科技专项(2014AAA013，2016AAA068)；湖北省自然科学基金资助项目(2014CFB598);高层次人才科研启动金资助项目(BSQD385);“先进制造技术与装备”协同创新中心开放基金资助项目(1201508)

TH161DOI：10.3969/j.issn.1004-132X.2017.03.003

吴震宇，男，1982年生。湖北工业大学机械工程学院副教授。主要研究方向为智能控制与数控技术。E-mail:wzy5221027@163.com。赵大兴，男，1962年生。湖北工业大学机械工程学院教授、博士研究生导师。钟瑞龄，男，1968年生。宜昌长机科技有限责任公司高级工程师。许 万,男，1979年生。湖北工业大学机械工程学院副教授。