吸力式组合桩抗拔承载特性数值分析*

黄绍梁， 杜 湧， 高建财

(太原理工大学 建筑与土木工程学院， 山西 太原 030024)

吸力式组合桩抗拔承载特性数值分析*

黄绍梁， 杜 湧， 高建财

(太原理工大学 建筑与土木工程学院， 山西 太原 030024)

吸力式组合桩的承载特性是海洋工程设计和施工中的一个关键问题， 通过采用有限元分析方法对吸力式组合桩的极限承载特性进行计算， 考虑了长径比、 荷载作用角度和荷载作用点三个重要因素. 探讨了荷载在不同长径比、 作用角度和作用点下吸力式组合桩的极限承载力， 根据承载力的变化规律得出最佳荷载作用点位置. 结果表明， 长径比越大， 吸力式组合桩的极限承载力越大； 荷载作用角度越小， 吸力式组合桩的极限承载力越大， 当荷载作用角度为0°时， 吸力式组合桩的极限承载力最大； 当荷载作用点从桩顶移动到桩底时， 极限承载力呈现先上升后下降的趋势， 且最佳荷载作用点位置随着长径比的增长会发生上移.

吸力式组合桩； 承载力； 有限元分析； 最佳荷载作用点

0 引 言

吸力式基础作为一种经济有效的海洋结构物基础形式受到广泛关注. 吸力式基础， 又称为吸力锚、 吸力桩、 负压锚或桶形基础， 它是一种大直径的圆筒结构， 通常底部敞开， 顶部封闭. 在安装过程中， 首先桩通过自身的重量嵌入海底土壤使得筒内形成初始封闭， 然后打开桩顶部的阀门， 将桩体内部的气体和水排出， 此时桩体内部形成负压， 在负压的作用下， 桩体可不断的被压入泥中， 直到贯入设计的深度. 为了适应不同的水深和土质条件， 通常会将多个吸力式单桩组合使用， 以形成更加稳固、 调节精度更高的吸力式组合桩结构. 相对吸力式单桩， 组合桩具有稳定性高、 可调性高和适用性广等优点. 与浅海平台相比， 在深海中吸力式组合桩所受到的锚系荷载显著增加， 主要承受上部结构受风浪荷载作用后传递下来的拉拔荷载. 因此， 研究吸力式组合桩的抗拔承载特性具有重要的科学意义和工程实用价值.

目前， 针对吸力式组合桩的研究比较少， 缺乏行业设计规范和统一标准[1-5]. 刘振纹等[6]分析了双桶基础的地基水平承载力， 并给出了相应的估算方法. 刘树杰[7]通过对海上风机多桶基础的承载力分析， 探讨了多桶基础在竖向、 水平和力矩作用下的极限承载力， 给出了荷载的最有利和最不利的作用方向. 李驰[8]等对多桶基础在竖向和水平荷载作用下的静承载力进行了研究， 提出对称多桶组合基础竖向和水平静承载力的确定方法， 但李驰只给出了一种长径比下多桩的抗拔承载力， 同时忽略了作用点和作用角度的影响. 为了弥补荷载作用点和作用角度对吸力式组合桩的影响， 本文选取了3种不同长径比的吸力式组合桩， 采用大型有限元软件ABAQUS进行三维非线性有限元数值分析， 分别对均质软粘土地基中荷载在吸力式组合桩桩身不同作用点和作用角度作用下的极限承载力进行了数值模拟. 通过数值分析吸力式组合桩在不同加载模式下的承载特性， 为今后的施工设计提供更为合理的建议.

1 有限元数值分析方法

考虑到吸力式组合桩结构和荷载的对称性， 采取吸力式组合桩与计算区域的一半简化有限元计算模型， 如图 1 所示. 整个模型采用三维8节点减缩积分实体单元以减少计算量. 为了消除边界效应的影响， 土体的计算区域桩径方向取10倍桩间距， 深度方向取5倍桩长； 为了提高计算精度， 在桩周及桩内部土体有限元划分得更密致， 其他位置沿径向增长. 桩体为线弹性材料， 弹性模量E=210 GPa， 泊松比v=0.3， 桩壁厚t=0.03 m， 桩的外径D=2.5 m， 桩间距S=5 m， 桩体的长径比L/D=2, 4, 6. 土体为均质软粘土， 假定土体处于完全不排水状态， 不排水强度Su=10 kPa， 采用Mohr-Coulomb屈服准则的理想弹塑性模型， 变形模量为E=500Su， 泊松比v=0.49， 内摩擦角为φ=26°， 剪胀角ψ=0°， 黏聚力取c=12 kPa， 认为土体是不可压缩的. 桩土之间的相互作用采用库伦摩擦对模拟， 吸力式组合桩与土体的法向接触面采用硬接触形式， 切向接触面采用罚函数法来模拟桩土之间的摩擦效应， 即桩壁的摩擦力与桩壁所受到的垂向压应力成正比. 有研究表明， 当摩擦系数f超过临界值0.4后， 摩擦系数对吸力桩承载力的影响很小[9]. 考虑到施工桩基础贯入的难度， 本模型中设定桩土之间的摩擦系数为f=0.35.

图 1 吸力式组合桩及有限元模型Fig.1 Triple clustered suction piles and finite element model

在有限元数值计算过程中， 有荷载控制方法和位移控制方法两种加载方法， 用位移控制方法加载可以得到更精准的荷载-位移曲线[10]. 当荷载-位移的斜率为0时， 意味着在荷载不变的情况下位移在持续增长， 即认为基础达到了极限平衡状态[11]. 因此， 本文采用位移控制施加荷载的方法进行加载.

2 吸力式组合桩承载力分析

下面选取了3种不同长径比的吸力式组合桩， 分别对不同荷载作用点和荷载作用角度下吸力式组合桩的极限承载能力进行了对比分析.

2.1 长径比的影响

针对长径比L/D=2, 4, 6的吸力式组合桩， 图2给出了水平荷载和竖直上拔荷载与位移之间的关系曲线. 从图 2 中可以看出， 长径比对吸力式组合桩的极限承载力影响很大， 随着长径比的增长， 吸力式组合桩的水平极限承载力和竖向抗拔承载力都有显著的增加. 从图 2(a) 中可以发现， 在后期的加载过程中， 长径比L/D=2的吸力式组合桩水平荷载-位移曲线斜率率先接近为零， 说明此时桩的水平承载能力已得到最大发挥， 地基发生破坏. 因此吸力式组合桩的长径比越小， 吸力式组合桩的水平承载力越小. 图 2(b) 中在竖直上拔的过程中， 吸力式组合桩的承载力主要是来源于桩土之间的摩擦力及桩和桩内土的自重， 当桩土之间的摩擦力达到极限值后， 桩身位移都会陡然发生增长， 说明此时桩体被拔出土体. 随着长径比的增长， 吸力式组合桩基础的竖向抗拔承载力也有所增长， 说明长径比是影响吸力式组合桩承载力的一个重要因素.

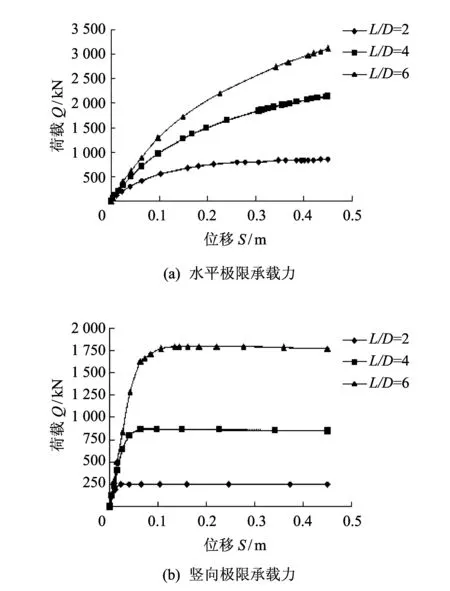
图 2 不同荷载作用方向的荷载-位移曲线Fig.2 Load-displacement curves of different loads

2.2 荷载作用角度的影响

图 3 是荷载作用点位置不同时， 吸力式组合桩极限承载力与荷载作用角度的关系曲线.

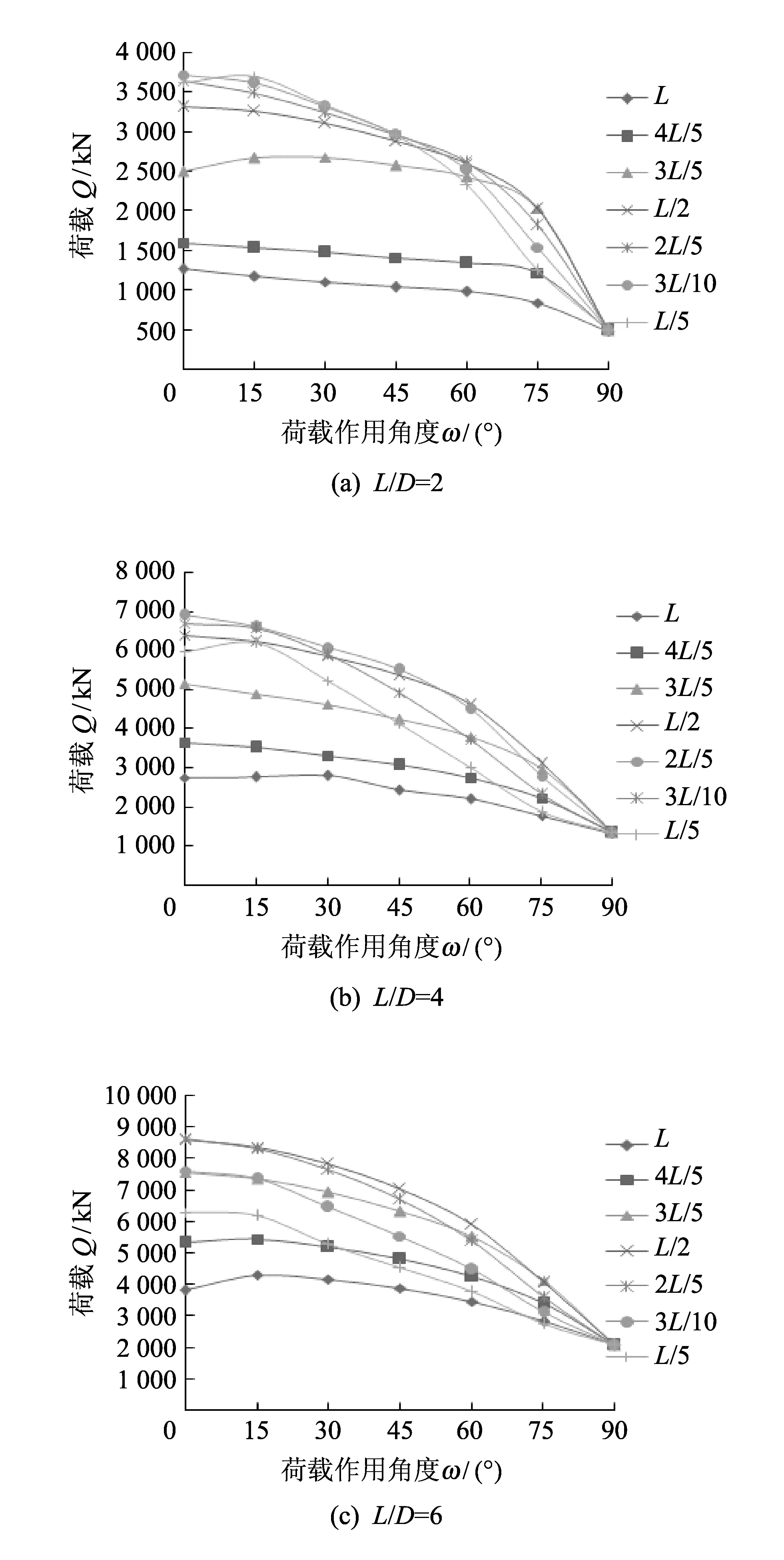
图 3 不同荷载作用角度的荷载-位移曲线Fig.3 Load-displacement curves of different loads

从图 3 中可以发现， 在同一荷载作用条件下， 在水平荷载作用下的承载力总是最大， 随着荷载作用角度的增大， 承载力一直在变小. 这说明在相同条件下， 吸力式组合桩的水平承载力比竖向抗拔承载力大. 这是由于在水平荷载作用下， 吸力式组合桩主要受桩侧被动土压力的作用， 而在竖直上拔荷载作用下， 荷载主要来自于桩土之间的摩擦力及桩和桩内土的自重. 因此， 荷载作用角度为0°是吸力式组合桩的最佳荷载作用角度. 但是在实际工程中， 深海海洋平台工程中很难做到水平荷载[12]. 因此， 在深海海洋平台的设计中， 应该尽量使作用在吸力式组合桩上的荷载接近水平.

2.3 荷载作用点的影响

图 4 为吸力式组合桩在不同荷载作用角度下荷载与作用点之间的关系曲线.

图 4 不同荷载作用点的荷载-位移曲线Fig.4 Load-displacement curves of different loads

从图 4 中可以发现， 吸力式组合桩的承载力随着荷载作用点位置的上升呈现先增大后减小的趋势， 而且长径比越大， 这种趋势越明显， 角度越小， 这种趋势也越明显. 在长径比L/D=2的吸力式组合桩中， 荷载作用点在z/L=0.3～0.55之间时， 吸力式组合桩的承载力最大； 在长径比L/D=4 的吸力式组合桩中， 荷载作用点在z/L=0.4～0.55之间时， 吸力式组合桩的承载力最大； 在长径比L/D=6的吸力式组合桩中， 荷载作用点在z/L=0.45～0.55之间时， 吸力式组合桩的承载力最大； 因此， 随着长径比的增大， 吸力式组合桩的最佳荷载作用点位置会发生上移. 当荷载作用角度为0°和15°时， 吸力式组合桩的承载力几乎没有明显的差异， 随着荷载作用角度的增大， 极限承载力也随之下降， 而且下降的速度也越来越大. 当长径比相同时， 荷载作用角度越大， 曲线越平缓， 说明荷载作用点位置对承载力的影响在减小.

3 结 论

1) 长径比的增长可以提高吸力式组合桩的水平承载力和竖向抗拔承载力. 吸力式组合桩在水平荷载和竖向上拔荷载作用下发生破坏时都是桩被拔出土体， 长径比越大， 桩体被拔出时产生的位移越大， 而水平位移也要比竖向位移大很多， 这些特征可以为吸力式组合桩基础的破坏标准作参考.

2) 在同一个作用点处， 荷载作用角度越小， 吸力式组合桩的极限承载力越大. 因此， 在实际工程中， 应该尽量将荷载作用方向接近于水平.

3) 随着长径比的增长， 最佳荷载作用点的位置会发生上移， 且最佳荷载作用点处的水平承载力最大. 当长径比相同时， 随着荷载作用角度的增大， 不同荷载作用角度下的最佳荷载作用点位置会发生上移.

[1]Clukey E C, Aubeny C P, Murff J D. Comparison of analytical and centrifuge model tests for suction caissons subjected to combined loads[C]. Cancun：Proceedings of the 22nd International Conference on Offshore Mechanics and Arctic Engineering， 2003.

[2]Ei-sherbiny R M. Performance of suction caisson anchors in normally consolidated clay[D]. Austin： The University of Texas at Austin, 2005.

[3]Wu Ke, Luan Maotian, Fan Qinglai, et al. Failure envelopes of bucket foundation subjected to combined loads[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(4)： 574-580.

[4]张永涛， 杨炎华， 黎冰， 等. 桥梁吸力式沉箱基础承载特性试验研究[J]. 岩土工程学报， 2015， 37(1)： 177-182. Zhang Yongtao, Yang Yanhua, Li Bing, et al. Model tests on bearing performance of suction caisson foundation for bridges[J]. Chinese Journal of Geotechnical Engineering, 2015， 37(1)： 177-182. (in Chinese)

[5]郑翔， 黎冰， 邱月. 吸力式沉箱基础抗拔破坏标准研究[J]. 科学技术与工程， 2013， 13(7)： 1868-1872. Zheng Xiang, Li Bing, Qiu Yue. Research on the uplift failure criterion of suction caisson foundation[J]. Science Technology and Engineering， 2013， 13(7)： 1868-1872. (in Chinese)

[6]刘振纹， 王建华， 秦崇仁， 等. 负压桶形基础地基水平承载力研究[J]. 岩土工程学报， 2000， 22(6)： 691-695. Liu Zhenwen, Wang Jianhua, Qin Chongren, et al. Research on the horizontal bearing capacity of bucket foundations[J]. Chinese Journal of Geotechnical Engineering, 2000， 22(6)： 691-695. (in Chinese)

[7]刘树杰， 王忠涛， 栾茂田. 单向荷载作用下海上风机多桶基础承载特性数值分析[J]. 海洋工程， 2010， 28(1)： 31-35. Liu Shujie, Wang Zhongtao, Luan Maotian. Numerical analysis of bearing capacity behavior of multi-bucket suctional foundation for offshore wind turbine under monotonic loading[J]. The Ocean Engineering, 2010， 28(1)： 31-35. (in Chinese)

[8]李驰. 软土地基桶形基础循环承载力研究[D]. 天津： 天津大学， 2006.

[9]王志云， 王忠涛， 栾茂田， 等. 吸力式沉箱基础极限拉拔承载力的数值分析[J]. 岩土力学， 2008， 29(6)： 1545-1550. Wang Zhiyun, Wang Zhongtao, Luan Maotian, et al. Numerical analysis of ultimate uplift bearing capacity behavior of suction caisson foundations[J]. Rock and Soil Mechanics, 2008， 29(6)： 1545-1550.(in Chinese)

[10]丁红岩， 翟少华， 张浦阳. 海上风电大尺度顶承式筒型基础承载力特性有限元分析[J]. 工程力学， 2013， 30(6)： 124-134. Ding Hongyan, Zhai Shaohua, Zhang Puyang. Finite element analysis of bearing capacity bearing of cover load bearing large scale bucket foundation for offshore wind turbines[J]. Engineering Mechanics， 2013， 30(6)： 124-134. (in Chinese)

[11]Zhao S F, Luan M T, Lu A Z. Numerical analysis of bearing capacity of foundation under combined loading[C]. Perth： University of West Australia, 2005.

[12]Tjelta T I. Suction piles： their position and applications today[C]. Proceedings of the 11th International Offshore and Polar Engineering Conference. Cupertino： International Society of Offshore and Polar Engineers, 2001.

Numerical Analysis of Ultimate Uplift Bearing Capacity of Triple Clustered Suction Piles

HUANG Shao-liang， DU Yong， GAO Jian-cai

(College of Architecture and Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

The bearing capacity of triple clustered suction piles is a crucial problem in the design and construction of marine engineering. By using the finite element analysis method, the ultimate bearing capacity of triple clustered suction piles was calculated with the aspect ratios, the loading inclination angle and the load attachment point considered. Under different aspect ratios, action angle and action points, the ultimate bearing capacity of triple clustered suction piles were discussed. According to the change law of bearing capacity, the optimum load action point was obtained. The results show that the larger the ratio of length to diameter, the greater the ultimate bearing capacity of triple clustered suction piles. The smaller the load angle, the greater the ultimate load capacity of the triple clustered suction piles, when the load angle is 0 degree, the ultimate bearing capacity of triple clustered suction piles is the largest. When the load point moves from the top to the bottom, the ultimate bearing capacity offers upgrade firstly than descending latter tendency. And the optimal load acting point position can move up with the increase of the ratio of the length to diameter.

triple clustered suction piles； bearing capacity； finite element analysis； optimum load attachment point

1673-3193(2017)01-0055-05

2015-10-30

山西省百人计划项目(800101-02030017)； 131人才专项经费(900198-02010018)

黄绍梁(1991-)， 男， 硕士生， 主要从事岩土工程方面的研究.

杜 湧(1956-)， 男， 教授， 博士， 主要从事海洋结构与基础工程方面的研究.

TU473.15

A

10.3969/j.issn.1673-3193.2017.01.011