非均匀Kerr介质中畸形波的特性研究*
2017-02-28薛亚奎
宋 妮, 薛亚奎
(中北大学 理学院, 山西 太原 030051)
非均匀Kerr介质中畸形波的特性研究*
宋 妮, 薛亚奎
(中北大学 理学院, 山西 太原 030051)
以Kerr介质中二维各向异性空间孤子的传输方程为研究对象, 对非均匀(2+1)维非线性薛定谔方程畸形波的动力学特性进行了分析和研究. 利用相似变换和直接假设, 构建出了非均匀(2+1)维非线性薛定谔方程的一阶、 二阶畸形波解, 深入讨论了畸形波在不同色散介质中的传播特性, 包括幅值和位置等. 所得结果可用于描述光纤中出现的一些物理现象.
畸形波; 相似变换; 非线性薛定谔方程; 动力学特性
0 引 言
畸形波, 也被称为奇异波、 怪波等, 最早起源于海洋动力学, 是指短时间存在的局部区域大振幅波动, 波峰尖, 波高大, 能量集中, 具有突发性、 不确定性等特点[1-2]. 畸形波广泛地存在于世界上各个海域, 对于采油平台、 船舶航运、 潜艇潜行有着巨大的危害, 因此有关畸形波的研究已成为波浪理论和非线性领域中的一个热点问题. 随着理论与实验研究的不断深入, 人们在其它科学领域中也发现了这一现象, 例如光学[3-4]、 玻色-爱因斯坦凝聚(BECs)[5]、 超流体[6]、 等离子体[7]、 表面张力波[8]、 激光器[9]、 多稳态系统[10]、 大气物理[11]和金融学中[12]等. 虽然在海洋环境中, 畸形波被认为是一种极具危害性的非线性波, 但在光波中却可以加以利用. Dudley等人[13]实现了在超连续谱系统中对光畸形波的控制和治理. Bludov等人[14]提出了在非线性波导阵列中将畸形波高效压缩光能的设想.
非线性薛定谔方程(NLSE)可以用来描述BECs、 非线性光学中的光脉冲传输、 非线性量子理论、 等离子物理和流体力学等很多物理现象. (1+1)维非线性薛定谔方程是可积的[15], 得到了稳定的孤子解, 因此该方程最早被人们熟知. 但关于高维如(2+1)维、 甚至(3+1)维非线性薛定谔方程, 类似的稳定解则很少有报道, 一个重要原因是其局域解是不稳定的. 但近十几年来, 非均匀(2+1)维非线性薛定谔方程的研究引起了人们很大兴趣, Towers等人[16]利用变分近似法和直接数值模拟法得到了稳定的2维孤子解. Zhong等人[17]得到了一类精确的空间孤子解, 该孤子解可以用来改进齐次平衡法和F-展开技术, 上述进展为进一步研究具有各种物理效应的变系数高维非线性薛定谔方程提供了充分的理论依据. 但就目前的文献而言, 有关非均匀(2+1)维非线性薛定谔方程畸形波的研究还不是很多. 鉴于此, 本文以Kerr介质中二维各向异性空间孤子的传输模型为基础, 对二维光学畸形波的非线性动力学特性作进一步展开和讨论.
1 Kerr介质中空间孤子的传输方程
在直角坐标系中, 描述Kerr介质中二维各向异性空间孤子的传输特性可用非均匀(2+1)维非线性薛定谔方程来表示, 其归一化形式为[18]
(1)
式中:u(t,x,y)表示光弹包络或物质波波包;t是归一化传输时间;x,y是归一化二维空间坐标;β1(t) 和β2(t)的物理意义取决于具体的物理模型. 在空间孤子模型中,β1(t)和β2(t)表示色散系数.γ(t) 表示Kerr非线性系数, 其值可以取正或取负. 当γ(t)>0时, 对应于聚焦非线性介质; 当γ(t)<0 时, 则对应于散焦非线性介质.g(t)表示增益或损耗系数, 它们都由系统本身的性质确定.
方程(1)也是一个Gross-Pitaevskii方程, 可用来描述玻色-爱因斯坦凝聚体中的物质波. 研究表明在周期性的光子晶体控制下, 方程(1)能够得到稳定的物质波.
2 相似变换和畸形波解
对复包络场u(t,x,y)构造如下形式的变换
(2)
其幅值为
(3)
式中:φR(t,x,y),φI(t,x,y)和相似波相位φ(t,x,y)是实待定函数.
将方程(2)代入方程(1), 得到耦合的变系数偏微分方程组
(4a)
(4b)
为计算实函数φR(t,x,y),φI(t,x,y)和相位φ(t,x,y), 引入新变量A(t),B(t),C(t),P(η,τ),Q(η,τ),h(t,x,y),η(t,x,y)和τ(t), 设
(5a)
(5b)

(5c)
其中,μ是一个常数.
将方程(5)代入方程(4), 得到方程组
(6a)
(6b)
进一步简化整理方程(6), 得到如下形式的方程组
(7a)
(7b)
(7c)
(7d)
(7e)
(7f)
式中:η(t,x,y),h(t,x,y),A(r),B(t),C(t),P(η,τ)和Q(η,τ)均是待定函数, 需计算其表达式.
利用代数运算求解方程(7a)~(7d), 有
(8a)
(8b)
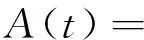
(8c)

(8d)
式中:a0,b,d是常数,δ1(t),δ2(t),δ0(t)是自由函数, 且δ1(t),δ2(t),δ0(t)和h0(t)都是t的实函数.
为求解方程(7e)~(7f),τ(t)和γ(t)分别需要满足以下条件
(9a)
(9b)
代入整理, 方程(7e)~(7f)变为
(10a)
(10b)
为得到方程(10)的解, 不妨假设μ=1. 利用文献[19]中的方法, 方程(10)的一阶有理函数解为
(11)
其中
(12)
进一步, 方程(10)的二阶有理函数解为
(13)
其中
(14)
(15)
(16)
综上, 将所求各变量代入方程(2)中, 得到非均匀(2+1)维非线性薛定谔方程的有理函数解即畸形波解的表达式
(17)
式中:h(t,x,y),A(t),τ(t),P(η,τ)和Q(η,τ)分别由方程(8b), (8c), (9a), (11)和(13)所确定.
3 畸形波的动力学特性
本节在方程(17)的基础上, 分析非均匀(2+1)维非线性薛定谔方程的一阶畸形波、 二阶畸形波的非线性动力学特性, 讨论色散系数β1(t),β2(t) 以及增益或损耗系数g(t)对畸形波的影响, 文中的变量均为无量纲.
3.1 一阶畸形波
将方程(8c)和(11)代入方程(17), 可以得到方程(1)的一阶畸形波解
(18)
其幅值可以表示为
(19)
利用方程(19), 讨论非均匀(2+1)维非线性薛定谔方程一阶畸形波的非线性动力学特性. 由于色散系数β1(t)和β2(t)是t的自由函数, 考虑到多维孤子的固有不稳定性, 根据实际物理需要, 有很大自由度, 因此不妨选取合适的衍射系数来展现不同形式的一阶畸形波.
为研究需要, 不妨假设a0=δ1(t)=δ2(t)=1,L=δ1x+δ2y=x+y, 即L为空间坐标x和y的线性组合.
首先研究常系数色散β1(t)=β2(t)=1和增益系数g(t)=0的情况. 由约束条件(9b), 可以得到非线性系数γ(t)=1. 此时, 方程(1)为(2+1)维常系数非线性薛定谔方程. 取δ0(t)=0.5t2, 将上述系数代入方程(19)中, 得到如图 1 所示的一阶畸形波和其等值高线分布图.

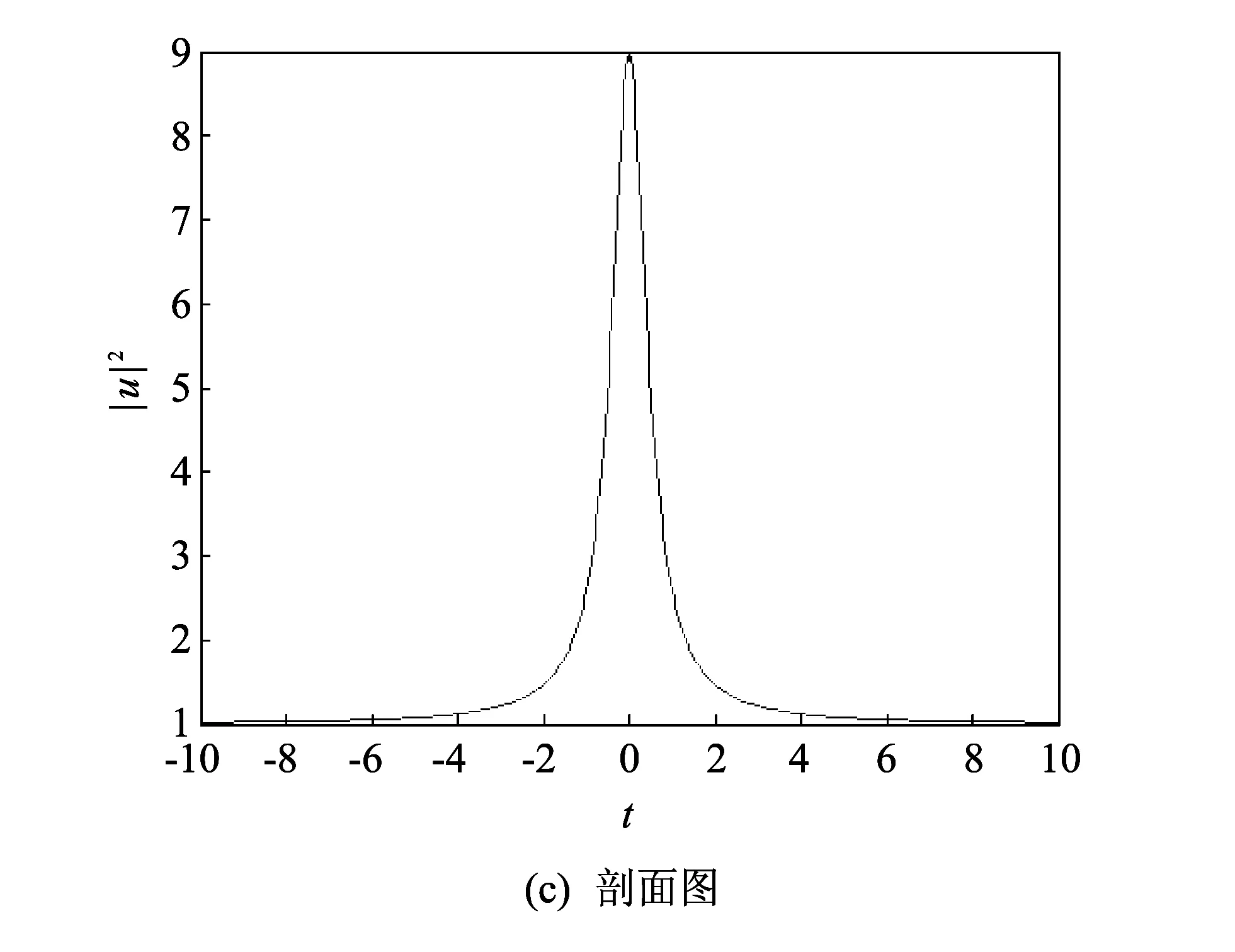
图 1 β1(t)=β2(t)=1, g(t)=0时的一阶畸形波Fig.1 The first-order rogue wave with the parameters β1(t)=β2(t)=1 and g(t)=0
由图1(a)可以看出, 畸形波在中心位置幅值突然增大, 随后快速消失, 存在时间极短. 图1(b) 为其等值高线分布图, 中心为畸形波幅值达到最大值的位置. 在方程(19)中, 令L=0, 畸形波幅值随坐标t的变化趋势如图1(c)所示. 从图中可以观察到畸形波在t=0 处幅值达到最大值, 最大幅值为9.
选取色散系数为雅克比椭圆函数的形式, 即β1(t)=sn(t,k),β2(t)=cn(t,k)和增益系数g(t)=0.05sint的情况, 由约束条件(9b), 可以得到非线性系数
(20)
取δ0(t)=t, 将上述系数代入方程(19)中, 得到如图 2 所示的一阶畸形波和其等值高线分布图.

图 2 β1(t)=sn(t,k), β2(t)=cn(t,k)和g(t)=0.05sin t 时一阶畸形波Fig.2 The first-order rogue wave with the parameters β1(t)=sn(t,k), β2(t)=cn(t,k) and g(t)=0.05sin t
由图2(a)可以看出, 一阶畸形波仍为单畸形波的形式, 突然出现, 随后快速消失. 在方程(19)中, 令L=0, 畸形波幅值随坐标的变化趋势如图2(b)所示. 从图中可以观察到畸形波在t=0处幅值达到最大值, 最大幅值也为9. 同时, 幅值的变化趋势和之前都不同, 在t=0的两侧, 幅值呈现出对称的规则变化.
3.2 二阶畸形波
将方程(13)~(16)代入方程(17), 可以得到方程(1)的二阶畸形波解
u=
(21)

其幅值可以表示为
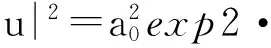
(22)
和一阶畸形波的情况类似, 选取不同的色散系数和增益系数来研究二阶畸形波的非线性动力学特性.
若色散系数β1(t)=sn(t,k),β2(t)=cn(t,k)和增益系数g(t)=0.05sint, 由约束条件(9b), 可以得到非线性系数
(23)
为研究方便, 在方程(23)中, 假设参数a0=1,δ1(t)=δ2(t)=0.8, 则L=δ1x+δ2y=0.8x+0.8y.
取δ0(t)=t, 将上述系数代入到方程(22)中, 得到如图 3 所示的二阶畸形波和其等值高线分布图. 从图3(a)中可以看出, 最高幅值的畸形波周围有4个比较小的峰值, 畸形波的所有能量都集中最高的幅值上, 并逐渐减弱. 图3(b)为其等值高线分布图, 4个小峰值在其四周呈两个“U”型对称分布, 中心为畸形波幅值达到最大值的位置. 在方程(22)中, 令t=0, 畸形波幅值随坐标的变化剖面图如图3(c)所示. 从图中可以看出, 畸形波在L=0处突然被激发达到最大幅值, 最大值为25. 令L=0, 得到畸形波幅值随坐标t的剖面图, 如图3(d)所示.

图 3 β1(t)=sn(t,k), β2(t)=cn(t,k)和g(t)=0.05sin t 时的二阶畸形波Fig.3 The second-order rogue wave with the parameters β1(t)=sn(t,k), β2(t)=cn(t,k) and g(t)=0.05sin t
这种情况下, 当t=0时, 畸形波幅值取得最大值, 最大幅值为25. 结果表明, 图3(b)中畸形波达到最大幅值的位置和利用数值模拟得到的剖面图是一致的.
4 结 论
利用相似变换构建了Kerr介质中非均匀(2+1)维非线性薛定谔方程的一阶、 二阶畸形波解, 研究了一阶、 二阶畸形波在Kerr介质中的传播特性. 在参数的调控下, 给出了畸形波幅值达到最大值的位置及对应的剖面图. 所得结果丰富了对畸形波的认识和了解, 对光畸形波、 光脉冲在非线性介质中的传播有潜在的应用价值.
[1]Osborne A R, Nonlinear ocean waves[M]. New York: Academic Press, 2009.
[2]Kharif C, Pelinovsky E, Slunyaev A. Rogue waves in the ocean[M]. New York: Observation, Theories and Modeling, 2009.
[3]SolliD R, Ropers C, Koonath P, et al. Optical rogue waves[J]. Nature, 2007, 450: 1054-1058.
[4]Genty G, DeSterke C M, Bang O, et al. Collisions and turbulence in optical rogue wave formation[J]. Physics Letters A, 2010, 374: 989-996.
[5]Yan Z Y, Konotop V V, Akhmediev N. Three-dimensional rogue waves in nonstationary parabolic potentials[J]. Physical Review E, 2010, 82: 036610.
[6]Ganshin A N, Efimov V B, Kolmakov G V, et al. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium[J]. Physical Review Letters, 2008, 101: 065303.
[7]Bailung H, Sharma S K, Nakamura Y. Observation of peregrine solitons in a multicomponent plasma with negative ions[J]. Physical Review Letters, 2011, 107: 255005.
[8]Xia H, Maimbourg T, Punzmann H, et al. Oscillon dynamics and rogue wave generation in faraday surface ripples[J]. Physical Review Letters, 2012, 109: 114502.
[9]Lecaplain C, Grelu P, Soto-Crespo J M, et al., Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser[J]. Physical Review Letters, 2012, 108: 233901.
[10]Pisarchik A N, Jaimes-Reategui R, Sevilla-Escoboza R, et al. Multistate intermittency and extreme pulses in a fiber laser[J]. Physical Review E, 2012, 86: 056219.
[11]Stenflo L, Marklund M. Rogue waves in the atmosphere[J]. Journal of Plasma Physics, 2010, 76: 293-295.
[12]Yan Z Y, Financial rogue waves[J]. Communications in Theoretical Physics, 2010, 54: 947-949.
[13]Dudley J M, Genty G, Eggleton B J. Harnessing and control of optical rogue waves in supercontinuum generation[J]. Optics Express, 2008, 16: 3644-3651.
[14]Bludov Y V, Konotop V V, Akhmediev N. Rogue waves as spatial energy concentrators in arrays of nonlinear waveguides[J]. Optics Letters, 2009, 34: 3015-3017.
[15]Kaup D J. A higher-order water-wave equation and the method for solving it[J]. Progress of Theoretical Physics, 1975, 54: 396-408.
[16]Towers I, Malomed B A. Stable (2+1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity[J]. Journal of the Optical Society of America B, 2002, 19: 537-543.
[17]Zhong W P, Xie R H, Belic M R, et al., Exact spatial soliton solutions of the two-dimensional generalized nonlinear Schrödinger equation with distributed coefficients[J]. Physical Review A, 2008, 78: 023821.
[18]Kruglov V I, Peacock A C, Harvey J D. Exact solutions of the generalized nonlinear Schrödinger equation with distributed coefficients[J]. Physical Review E, 2005, 71: 056619.
[19]Peregrine D H. Water waves, nonlinear Schrödinger equations and their solutions[J]. Journal of the Australian Mathematical Society, Series B, 1983, 25: 16-43.
Research on Rogue Waves in Inhomogeneous Kerr Medium
SONG Ni, XUE Ya-kui
(School of Science, North University of China, Taiyuan 030051, China)
Focusing on the transmission equation of the two-dimension anisotropy spatial soliton in the Kerr medium, nonlinear dynamic behaviors of the rogue waves for the (2+1)-dimensional nonlinear Schr?dinger equation were analyzed and studied. The similarity transformation and direct hypothesis were used to construct the first-order and second-order rogue waves solutions. On the basis of the solutions, transmission characteristics of the rogue waves were discussed in view of different types of dispersive medium, including amplitude and location. It can be applied to describe the physical phenomena in the optical fibers.
rogue waves; similarity transformation; nonlinear Schrödinger equation; dynamic behaviors
1673-3193(2017)01-0009-06
2016-04-08
山西省自然科学基金资助项目(2015011009)
宋 妮(1979-), 女, 讲师, 博士, 主要从事非线性动力学研究.
O175
A
10.3969/j.issn.1673-3193.2017.01.002
