数形结合思想在高中数学教学中的应用

程镘潜

【摘要】《普通高中数学课程标准（实验稿）》中提到了“了解概念、结论等产生的背景，体会其中所蕴含的数学思想方法，以及它们在后续学习中的作用”。由此可见，新课改以来，逐渐加强了对高中数学教学的重视程度。而数形结合是数学四大思想方法之一，同时也是高中数学学习的精髓，对于高中数学教学效果和质量的提高有着十分重要的促进作用。基于此，本文从多方面着手，概述了数形结合思想在高中数学教学应用中存在的误区，分析了如何将数形结合思想切实的应用到高中数学教学中。

【关键词】数形结合  高中数学教学  应用

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2016）35-0101-02

一、数形结合思想在高中数学教学应用中存在的误区

现阶段，数形结合的思想已经普遍应用到高中数学的教育教学过程中，但是通过总结和调查研究可以发现，数形结合思想在高中生实际解决数学问题时依旧存在一些误区，影响了解题的准确性和效率，主要表现为以下几点：

第一，画图比较草率，不等价的转化，不恰当的选择，片面的思考问题。

第二，应用数形结合思想解题的过程中出现了图像失真的问题，或者说不够简介，从而进入了死循环的解题状态。

第三，树形分裂，审题不够清晰，构图也不恰当，影响了解题的速读和准确性。

第四，在实际解题的过程中考虑的不够完善，理解的也不够深刻，所以在应用的过程中出现了定位不准确，引用不可靠等一系列问题和失误。

二、数形结合思想在高中数学教学中的应用

由上述分析可知，在应用数形结合思想结局数学问题的过程中，由于种种主客观因素会出现一系列的问题和失误，严重影响了解题的准确性和效率。基于此，笔者就如何将数形结合的思想切实的应用到高中数学的解题过程中去进行了如下分析和研究：

1.数形结合思想在集合中的应用

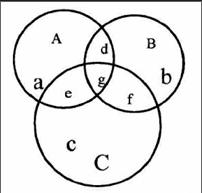
集合是高中数学中的重要组成部分，是一项基础性和重要性的内容。而数形结合思想在集合中的应用能够把抽象的问题具体化，能够让学生更直观的了解集合之间的关系。现阶段，韦恩图和数轴是我们解决集合问题中常用的图形。

例如，某学校高一（2）班40名学生报名参加语文、数学、英语三个课外学习小组，报名情况如下：

①40名学生每人至少报名参加一个课外学习小组;

②在没有报名参加语文小组的学生中，报名参加数学小组的人数是报名参加英语小组的二倍;

③仅报名参加语文小组的人数比余下的学生中报名参加语文小组的多一人;

④仅报名参加一个学习小组的学生中有一半没有报名参加语文小组。

问：①仅参加数学学习小组的有几人？

②有几人报名参加了语文学习小组？

此问题是高中数学中比较常见的一类问题，可以看出，一个题目中存在着错综复杂的数量关系，而如果用一般的方法就很难解决上述问题，因此，就可以通过数形结合的方式来解决此问题。可以设集合A为报名参加语文学习小组的人数，集合B为报名参加数学学习小组的人数，集合C为报名参加英语学习小组的人数。同时，可以结合下图来求解。

这样一来就可以显而易见的发现其中各个数量的关系，相关的问题也就迎刃而解了。

2.数形结合思想在函数求中的应用

函数也是高中数学中的重要组成部分，占据着很大的比例，而函数不仅理论性比较强，而且涉及的范围也比较广泛，所以说，函数的学习成为了很多学生的难题。所以，在结合函数的相关问题时将数形结合的思想应用其中也能够将复杂的题目简单化，并且变得显而易见，这对于函数问题的解决也是十分重要的。但是在应用数形结合的思想解决函数的相关问题时，教师要通过典型的例题来纠正学生容易犯的错误，做到有问题及时发现，即使解决，以避免学生在今后的解题过程中出现的各种失误和错误。

3.数形结合思想在不等式中的应用

应用数形结合的思想解决不等式的相关问题也是比较常用的一种高中数学教学方法，主要是通过写出相应不等式所代表的函数，绘制函数图像，观察图像与坐标轴的交点，或者图像与图像之间的交点来解决不等式的相关问题。需要注意的是，在利用数形结合的思想解决不等式的相关问题时，一定要确保图形的精确性，同时，在解题的过程中要做到善于观察善于发现问题，并在解题的过程中善于总结经验，也只有这样，才能确保类似问题的顺利解决。同时，为了让学生能够充分的应用图形来解决不等式的相关问题，就需要教师通过加强对学生数形互化能力的培养来激发其学习热情和积极性，使其能够更好的发现问题、整理与归纳问题，并将数形结合的思想灵活的应用到各类数学问题的解题过程中去。

三、结语

总之，数形结合思想在高中數学教学中的应用确实对于高中数学教学效果和质量的提高有着一定的促进作用，但是，在实际应用的过程中由于一些理解的偏差、人为的失误以及其他主客观因素致使其并没有实现价值最大化，所以，作为高中数学教育工作者一定要明确自身的责任和重任，做好引导和鼓励的工作，及时的纠正错误，在确保数形结合思想在高中数学教学中实现价值最大化的同时促进高中数学实现更好的发展和进步。

参考文献：

[1]罗开平.探究数形结合思想在高中数学教学中的应用与拓展.[J].《读与写：上，下旬》2016，13（18）

[2]张忠德.新课改下高中数学课程中数形结合思想的运用.[J].《速读旬刊》.2016（1）