基于广义西格摩德模型研究沥青混合料动态模量和相位角主曲线*

陈 辉 罗 蓉 刘涵奇 吕慧杰 冯光乐

(武汉理工大学交通学院1) 武汉 430063) (湖北省交通厅工程质量监督局2) 武汉 430014)

基于广义西格摩德模型研究沥青混合料动态模量和相位角主曲线*

陈 辉1)罗 蓉1)刘涵奇1)吕慧杰1)冯光乐2)

(武汉理工大学交通学院1)武汉 430063) (湖北省交通厅工程质量监督局2)武汉 430014)

针对目前国内评价沥青混合料粘弹性性质时关注动态模量而忽略相位角的性质这一问题，对动态模量主曲线绘制方法进行完善并补充相位角主曲线绘制方法.采用4种沥青混合料试件进行单轴压缩动态模量试验，确定基于广义西格摩德模型的动态模量主曲线和存储模量主曲线，最后根据2种模量主曲线拟合参数计算得到相位角主曲线模型方程.结果表明，在动态模量和存储模量主曲线确定前提下，相位角主曲线拟合情况良好，反映出该方法绘制相位角主曲线是可行的.

沥青混合料；动态模量；存储模量；相位角；主曲线

0 引 言

我国目前的沥青路面设计方法是以层状体系理论为基础，根据规范采用20 ℃时的抗压回弹模量计算弯沉值，并采用15 ℃时的抗压回弹模量计算弯拉应力，从而获取沥青路面的材料参数.但由此得到的沥青混合料材料参数与实际路面承受荷载能力存在差异.而在美国ASSHTO沥青路面设计方法中，提出采用动态模量作为沥青混合料力学性质指标，更贴近路面加载状态[1].

沥青混合料是一种典型的粘弹塑性材料，其力学性质受温度和频率影响，并在高温低频与低温高频条件下展现出等效的粘弹性性质.借助时间-温度等效原理绘制主曲线可将试验有限的加载频率和温度条件下的动态模量和相位角扩展至更加广泛的频率域和温度域范围内，从而更加全面地认识沥青混合料的粘弹性性质[2].许多学者在研究动态模量主曲线时，忽视相位角的性质[3]，或者采用不相关的模型拟合并绘制相位角主曲线，导致得到的动态模量主曲线和相位角主曲线本应统一的物理意义存在较大偏差[4].

文中采用ASSHTO试验方法研究沥青混合料的动态模量和相位角，同时采用修正西格摩德模型绘制动态模量主曲线，并在该模型基础上推导相应相位角主曲线模型，从而绘制相位角主曲线，更加准确地分析沥青混合料的粘弹性性质.

1 动态模量及相位角主曲线

1.1 复数模量

确定沥青混合料的动态模量通常来自于其复数模量.复数模量是沥青混合料的基本材料属性，由实部和虚部组成，其实部表征弹性性质，称为存储模量，虚部表征粘性性质，称为损失模量，见式(1)[5].

(1)

式中：E*为复数模量，MPa；E′和E″分别为存储模量和损失模量，MPa.

沥青混合料复数模量的模(即绝对值)定义为动态模量，反应沥青混合料的强度特性，即

(2)

复数模量中损失模量与储存模量的比值定义为相位角的正切值，见式(3).相位角可反映沥青混合料受到正弦波荷载时，在一个周期内应变滞后于应力的相位差.通常来说，对于弹性材料，相位角等于0°；对于粘性材料，相位角等于90°；对于粘弹性材料，相位角在0°～90°区间范围内变化[6].

(3)

式中：φ为相位角，(°).

存储模量和损失模量皆可用动态模量和相位角表示，即

(4)

(5)

1.2 动态模量主曲线模型

绘制沥青混合料动态模量主曲线的理论依据是时间-温度等效原理.通过时温等效原理可将沥青混合料在各自温度条件下不同加载频率的动态模量数据点构成的曲线平移至参考温度下形成一条光滑的动态模量曲线，称为在该参考温度下的动态模量主曲线.利用动态模量主曲线能够拓展得到更宽广温度频率范围下的动态模量.不仅是动态模量主曲线，存储模量和相位角主曲线皆如此，根据有限的试验数据便能获知其他未知环境条件下沥青混合料的力学性质[7].

运用时温等效原理的关键在于确定移位因子αt.将原频率处的动态模量平移至参考温度下对应的频率即缩减频率fr.其中缩减频率和移位因子之间的关系见式(6).同时采用W.L.F方程计算移位因子，见式(7)[8].

(6)

式中：f为试验的加载频率，Hz；fr为对应的参考温度下的缩减频率，Hz.

(7)

式中：C1，C2为由拟合确定的材料常数；t为试验温度， ℃；t0为参考温度，℃.

关于动态模量主曲线的拟合模型，本文采用广义西格摩德(Generalized Logistic Sigmoidal)模型[9]，模型表达式见式(8).

(8)

1.3 相位角主曲线模型

有研究表明，动态模量和存储模量在加载频率趋近于无穷大时接近于最大值，而在加载频率趋近于0时接近于最小值，因而存储模量同动态模量一般具有相同的变化趋势，其主曲线模型亦可用广义西格摩德模型表征，即

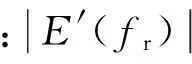
然而，损失模量及相位角在加载频率趋近于无穷大以及加载频率趋近于0时都接近于0，根据动态模量、存储模量和损失模量之间的关系,见式(3)，此时的动态模量等于存储模量[10].因此，上述动态模量和存储模量主曲线模型中参数满足关系式δ=δ1和α=α1.

根据式(4)及上述参数关系可求得基于广义西格摩德模型的相位角主曲线模型，即：

因此，只要分别拟合得到动态模量主曲线和存储模量主曲线模型参数以后，即可根据式(10)计算并绘制相位角主曲线模型.

2 试验方案

2.1 试验材料和试件成型

本试验采用的集料为石灰岩和辉绿岩，沥青为70#基质沥青和SBS改性沥青，各材料性能均满足规范要求.石灰岩选用AC-20C级配而辉绿岩选用AC-13C级配制备沥青混合料试件，通过马歇尔试验确定最佳油石比为4.3%，具体矿料级配见表1～2.

试验采用Superpave旋转压实成型，原始试件尺寸为直径150 mm、高度170 mm，经钻心切割后获得尺寸为直径100 mm、高度150 mm的圆柱体试件.试件空隙率应保证控制在4%±0.5%范围内.

2.2 试验步骤

本试验方案中的单轴压缩动态模量试验参照美国AASHTO TP62-07规范，试验温度分别为-10,4.4,21.1,37.8和54.4 ℃；加载频率分别为0.1,0.5,1,5,10,25 Hz；试验通过MTS对试件施加半正弦荷载，并采用应力控制模式施加荷载同时控制应变在50×10-6～100×10-6范围以内从而保证试验为无损试验.按照上述方案进行试验依次记录试验原始数据并计算各温度和频率条件下的动态模量和相位角.

表1 石灰岩AC-20C沥青混合料级配组成

表2 辉绿岩AC-13C沥青混合料级配组成

3 试验结果及分析

完成所有单轴压缩动态模量试验后，通过数据处理计算得到各沥青混合料试件的动态模量和相位角，以石灰岩70#沥青混合料试件为例，其动态模量和相位角分别见表3～4.

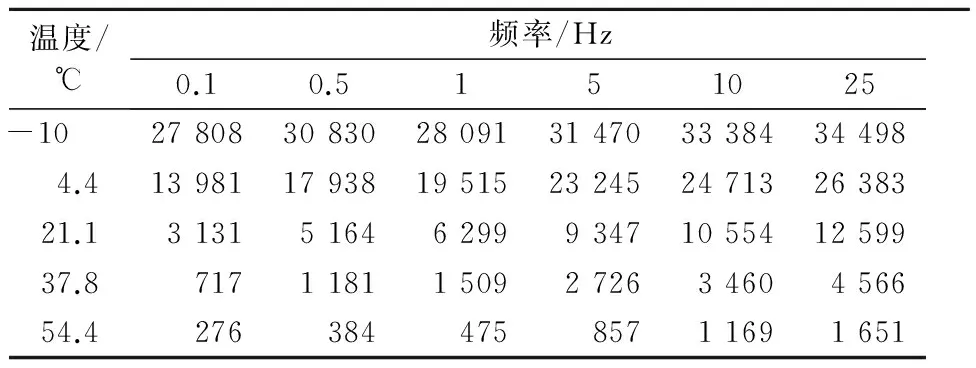
表3 AC-20C 70#沥青混合料动态模量 MPa

表4 AC-20C 70#沥青混合料相位角 (°)

本试验以21.1 ℃为参考温度绘制动态模量主曲线，利用相对误差法对模型以及移位因子中的拟合参数进行规划求解，并通过判定系数R2评判广义西格摩德模型的拟合优度.以石灰岩70#沥青混合料试件为例，按照上述步骤绘制出动态模量主曲线，见图1.

石灰岩70#沥青混合料动态模量主曲线方程见式(12).

由式(11)可知，动态模量主曲线拟合优度高，能够真实地反映该试件动态模量随着温度和频率的变化情况.接着利用测量的动态模量和相位角根据式(4)计算存储模量数值，并根据广义西格摩德模型拟合存储模量主曲线参数.其中需要注意的是，由于动态模量和存储模量均表征沥青混合料的粘弹性性质，具有统一的物理意义，因此各频率条件下的模量经平移至缩减频率时位置也应是统一的，即存储模量各温度条件下的移位因子是与动态模量相等的.一旦动态模量移位因子方程参数确定，存储模量移位因子方程参数也就随之确定不变.按照上述要求绘制的存储模量主曲线见图2.

图1 石灰岩70#沥青混合料动态模量主曲线

图2 石灰岩70#沥青混合料存储模量主曲线

70#沥青混合料存储模量主曲线方程为

因为动态模量主曲线参数的确定，导致存储模量主曲线在拟合前已经确定了4个参数，而只有β1，γ1和λ1尚未确定，规划求解时只需设置3个变量参数即可.在该前提下，存储模量的拟合优度仍很高，同时也保证了存储模量与动态模量主曲线缩减频率相同这一物理意义.

随着动态模量和存储模量主曲线模型所有参数的确定，相位角主曲线模型中的参数随之确定.根据式(10)绘制相位角主曲线，见图3.

图3 石灰岩70#沥青混合料相位角主曲线

基质沥青混合料相位角主曲线方程为

不同于动态模量主曲线和存储模量主曲线，相位角主曲线先随着加载频率的增大而增大至最高点，接着随着加载频率的增大而迅速减小.这是因为在低温条件下，沥青混合料主要受沥青胶结料影响，随着温度增大粘性增强从而相位角增大；在高温条件下，沥青混合料变软，胶结料劲度对混合料模量影响变弱，矿料骨架的嵌挤作用对混合料模量影响增强，因此相位角减小.

由图3可知，相比于动态模量和存储模量，相位角的测量数据分布规律并不规则，时常出现在单一温度条件下相位角变化呈现整体上升或下降趋势但存在突变点的情况，因此,相位角主曲线确定时无法满足突变点的要求从而拟合度并没有动态模量和存储模量主曲线高.另外由于相位角的模型参数全部由动态模量和存储模量模型参数确定，并不需要拟合，因而拟合优度不如前两者高.但相位角主曲线判定系数高于0.9仍属于拟合优异，同时三者还保持了统一的缩减频率更符合材料的物理意义.具体各种沥青混合料试件主曲线拟合参数汇总见表5，3种主曲线判定系数见表6.

表5 主曲线拟合参数汇总

表6 主曲线判定系数汇总

由表6可知，基于广义西格摩德模型绘制相位角主曲线对多种沥青和集料组成的沥青混合料均是可行的.因此，不论是从理论角度上来看，还是从实际工程运用角度来看，采用该方法一并绘制沥青混合料的动态模量、存储模量和相位角主曲线模型是行之有效的.

4 结 论

1) 沥青混合料的相位角不同于动态模量和存储模量，随着温度的升高总体呈现而增大的趋势，但随着频率的升高而先升高后降低.

2) 在相同环境条件下，SBS改性沥青混合料的相位角明显低于70#沥青混合料，说明70#沥青混合料的粘性强于改性沥青混合料.

3) 采用广义西格摩德模型绘制相位角主曲线时，只需先确定动态模量主曲线和存储模量主曲线参数即可.并且基于广义西格摩德模型绘制动态模量和存储模量主曲线再确定相位角主曲线这种方法，不仅绘制得到的主曲线拟合情况良好，而且具有统一的物理意义，从而更加准确地描述沥青混合料的粘弹性性质.

[1]黎晓，梁乃兴，陈玲.沥青混凝土动态模量及时-温等效方程[J].长安大学学报(自然科学版)，2014，34(3)：35-40.

[2]马林，张肖宁.间接拉伸与单轴压缩模式沥青混合料动态模量比较分析[J].公路交通科技，2009，26(10)：11-17.

[3]ZHU H, SUN L, YANG J, et al. Developing master curves and predicting dynamic modulus of polymer-modified asphalt mixtures[J].Journal of Materials in Civil Engineering,2011,23(2):131-137.

[4]马翔，倪富健，陈荣生.沥青混合料动态模量试验及模型预估[J].中国公路学报，2008，21(3)：35-39.

[5]赵延庆，吴剑，文健.沥青混合料动态模量及其主曲线的确定与分析[J].公路，2006(8)：163-167.

[6]冉武平，孔二春.环氧沥青混合料动态模量时温特性[J].中外公路，2015(6)：282-285.

[7]王昊鹏，杨军，施晓强，等.高模量沥青混合料动态模量及其主曲线研究[J].公路交通科技,2015，32(8)：12-17.

[8]YUSOFF N I M, CHAILLEUX E, AIREY G D. A comparative study of the influence of shift factor equations on master curve construction[J]. International Journal of Pavement Research and Technology,2011,4(6):324-336.

[9]ROWE G, BAUMGARDNER G, SHARROCK M. Functional forms for master curve analysis of bituminous materials[C]. Proceedings of the 7th International RILEM Symposium on Advanced Testing and Characterization of Bituminous Materials, Rhodes, Greece,2009.

[10]刘慧.沥青混合料粘弹性质及其对路面力学响应的影响[D].大连：大连理工大学，2014.

Research on Dynamic Modulus Master Curve and Phase Angle Master Curve of Asphalt Mixture Based on Generalized Logistic Sigmoidal Model

CHEN Hui1)LUO Rong1)LIU Hanqi1)LYU Huijie1)FENG Guangle2)

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)1)(EngineeringQualitySupervisionBureau,TransportationDepartmentofHubeiProvince,Wuhan430014,China)2)

Targeting at the problem that the current viscoelastic properties evaluation methods in China pay only attention to the dynamic modulus but neglect the phase, the dynamic modulus master curve drawing method is improved to determine the phase angle master curve. Uniaxial dynamic modulus tests are performed for four types of asphalt mixtures, the results of which are used to determine the dynamic modulus and storage modulus master curve based on the generalized logistic sigmoidal model. Besides, the master curve fitting parameters are used to calculate the phase angle master curve model equations. The results indicate that the master curve fitted is in good condition in the premise of certain dynamic modulus and storage modulus master curve, which reflects that the method is feasible in drawing the phase angle master curve.

asphalt mixture; dynamic modulus; storage modulus; phase angle; master curve

2016-11-18

*973计划青年科学家专题项目资助(2015CB060100)

U416.217

10.3963/j.issn.2095-3844.2017.01.028

陈辉(1994—)：男，硕士，主要研究领域为路面材料