一种IGBT传热模型参数等效计算方法*

刘宾礼 罗毅飞 汪 波 孟庆云 朱俊杰

(海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033)

一种IGBT传热模型参数等效计算方法*

刘宾礼 罗毅飞 汪 波 孟庆云 朱俊杰

(海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033)

以电力电子装置应用领域对IGBT模块传热特性及其散热设计的需求为牵引，基于Foster与Cauer热网络的结构属性与相互转换方法，建立了一种IGBT传热模型参数等效计算方法并进行了实验验证，对其传热特性进行了研究，得出封装各层温度运行规律及其各层之间的相互作用关系；建立了一种IGBT散热器传热模型参数设计方法并查明了最高结温、波动范围随散热器热容的变化规律.

热网络结构；等效计算；结温运行规律；散热设计

0 引 言

IGBT器件产生的功耗以热量的形式通过芯片、焊料层、铜层、陶瓷层和基板传递至散热器和外部空间.研究IGBT器件热量传递过程的作用机制，建立封装结构参数等效计算方法与散热器设计方法，对于指导制造者改进器件的散热性能，指导使用者合理设计散热装置、

开展结温预测和设定运行条件[1-7]，具有重大的理论意义和应用价值.

商业IGBT模块附带的数据手册中包含Foster热网络结构参数，是通过出厂前测试模块的瞬态热阻抗曲线得出的，采用该结构参数可以对IGBT模块的结温运行规律进行仿真，但其不具有实际物理意义，不能反映IGBT模块封装各层的热阻与热容情况，不能有效指导用户开展热特性与热设计研究.而Cauer热网络结构与IGBT模块实际封装各层存在一一对应关系，通过该结构可以对IGBT模块封装各层温度运行规律进行研究，可以有效指导模块与散热器开展热设计研究.因此，文中通过研究Foster与Cauer热网络本身的结构属性及其相互转换方法，建立了一种IGBT模块封装结构传热模型参数等效计算与散热器传热模型参数设计方法.并对IGBT结温与封装各层温度运行规律、散热器传热模型参数与结温之间的规律进行了研究.

1 IGBT传热模型参数等效计算方法

1.1 IGBT传热模型结构研究

Foster与Cauer热网络结构见图1.由Foster热网络结构转化为Cauer热网络结构的方法如下.

图1 IGBT模块热网络结构

Foster热网络结构热阻抗，见式(1).

(1)

对式(1)进行通分求和，得式(2).

(2)

则Z(s)导纳，见式(3).

(3)

当s→∞时，

(4)

通过式(4)即可得出Foster热网络结构对应的Cauer热网络结构中，第一层的热容，见式(5)[8-9].

(5)

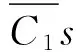
(6)

则Y*(s)阻抗，见式(7).

(7)

进而，当s→∞时，

(8)

通过式(8)即可得出Foster热网络结构对应的Cauer热网络结构中，第一层的热阻，见式(9).

(9)

(10)

以2阶RC热网络模型为例，采用功率幅值500 W，周期10 ms，占空比0.5，仿真时长200 ms，对图2a)Foster热网络结构按照上述方法等效变换为Cauer热网络结构(图2b))的正确性与准确性进行了仿真验证，仿真结果与误差分析，见图3.

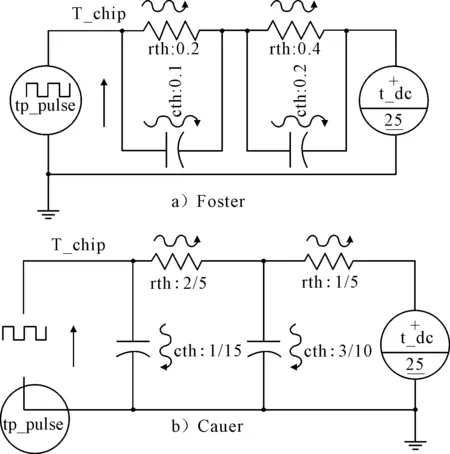
图2 热网络结构等效变换

图3为Foster与Cauer热网络结构等效变换前后仿真结果与误差分析，由图3可知，Foster热网络结构仿真结果与等效变换之后的Cauer热网络结构仿真结果吻合良好，在结温波动上升初期，存在微小误差，可以忽略不计.因此，验证了Foster与Cauer热网络结构等效变换方法的正确性与准确性.

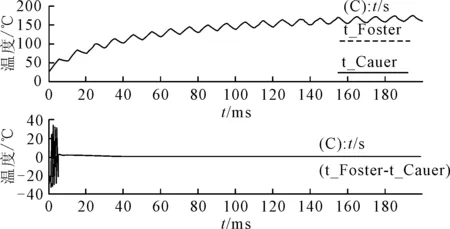
图3 Foster与Cauer热网络结构等效变换前后 仿真结果与误差分析

1.2 IGBT封装结构参数等效计算研究

对IGBT模块数据手册或实验测试得到的瞬态热阻抗曲线进行拟合，即可得到其Foster热网络结构参数.进而，采用1.1中Foster热网络结构转化为Cauer热网络结构的方法，即可得到IGBT模块封装各物理层或主要物理层的热阻和热容，用于IGBT模块结温运行规律与失效分析研究.

以某型600 V/50 A IGBT模块为例，采用电流源为IGBT模块加热，当芯片结温达到恒定后，切断电流源，此时接通热敏电参数测试结温用小电流源，实时对芯片结温进行测试，所得结温测试结果用于热阻抗计算[10-11].IGBT模块瞬态热阻抗理论表达式，见式(11).

(11)

式中，IGBT芯片结温Tj通过热敏电参数法获取.即在小电流条件下，IGBT芯片结温与集射极饱和压降VCE呈线性变化规律.实验用某型600 V/50 A IGBT模块热敏电参数法标定曲线，见图4a)，通过实验测得的定标曲线即可得到结温随饱和压降的线性变化规律，见式(12).IGBT模块壳温TC通过布置于芯片底板下方的热电偶获取.IGBT模块损耗P为饱和压降VCE与导通电流IC的积分.

图4 热敏电参数法标定曲线与瞬态热阻抗曲线

Tj=268.7-446.9·VCE

(12)

依据式(11)，采用热敏电参数法与相应的数据处理方法，即可得到该型IGBT模块的瞬态热阻抗曲线，见图4b).进而，以Foster热网络模型的瞬态热阻抗表达式(13)为目标函数进行曲线拟合，得到Foster热网络模型中的热阻和热容参数，见表1.

(13)

采用1.1 Foster热网络结构向Cauer热网络结构的转换方法，将该型IGBT模块Foster热网络结构(见表1)转化为Cauer热网络结构，见表2.该模型结构可对IGBT实际封装结构进行表征.

表1 Foster热网络模型参数

表2 Cauer热网络模型参数

该型600 V/50 A IGBT模块为课题组长期实验验证对象，其封装结构及其参数，已通过协调厂家获取，因此，采用已知结构与参数对本文的参数等效计算方法进行了验证.其封装为7层结构，由于其中几层时间常数与相邻层相比，非常小，可以忽略不计.因此，这些层热容支路视为开路状态，而热阻与相邻层合并.采用这种方法进行简化之后的Cauer热网络模型为3层结构，见图5.

图5 某型600 V/50 A IGBT模块Cauer热网络 结构、参数与简化过程

图5中A为该模块完整7层Cauer热网络结构与参数，这些参数通过物理测量与材料物理属性获取，过程复杂，适用于理论与实验研究阶段.B和C分别为7层模型简化之后的热网络结构与参数.通过对比表2与图5中C模型参数可以看出，采用Foster热网络转化为Cauer热网络之后的参数与IGBT模块实际物理层参数吻合较好，验证了该方法的正确性与准确性.

1.3 IGBT传热模型仿真与实验验证

针对该型IGBT模块，采用Foster热网络结构转为Cauer热网络结构之后的模型结构与参数，如表2与图5中C模型参数所示.采用红外热像仪测温法，对转化之后模型的正确性与准确性进行了实验验证.进而，基于Saber仿真平台，对其传热特性进行了仿真研究.

采用恒定可调节电流源作为打开封装的IGBT模块的输入，实验过程中对饱和压降和电流进行积分，积分所得功率作为仿真模型的输入，并采用红外热像仪对IGBT芯片温度进行实时测试.IGBT器件Cauer热网络结构仿真与实验电路见图6.

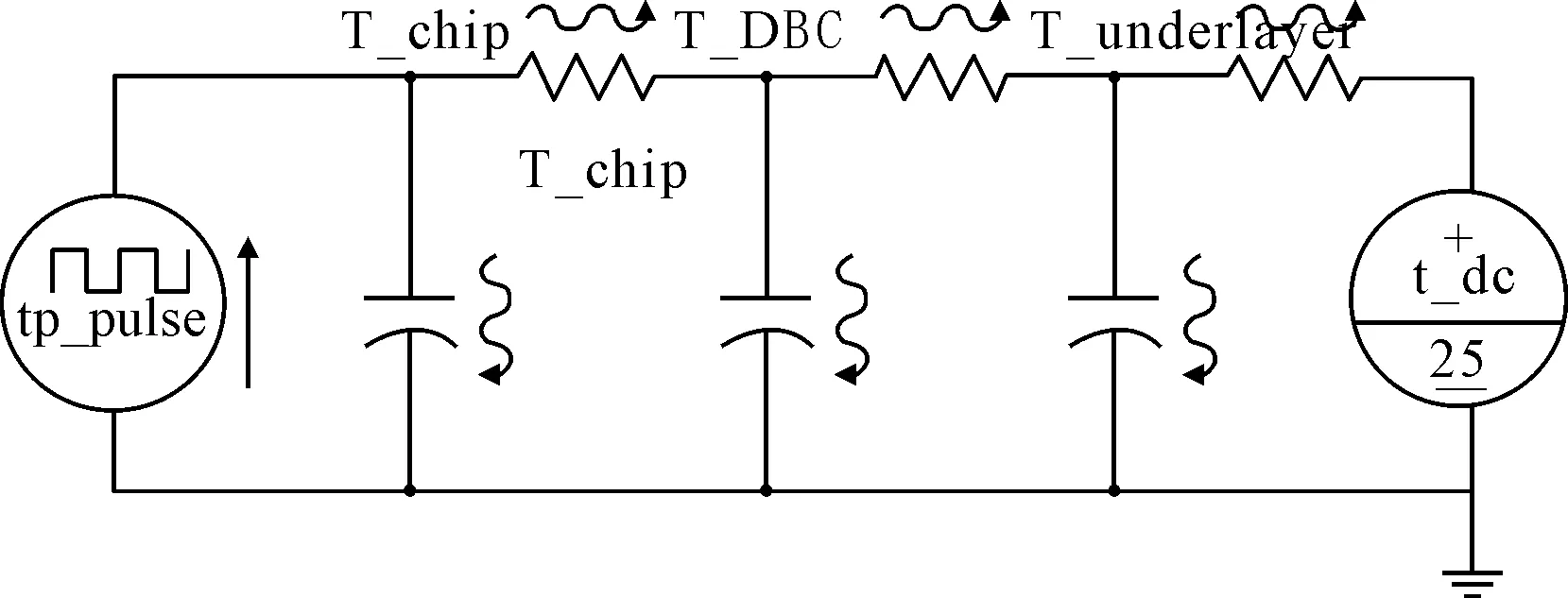
图6 仿真与实验电路

恒流源输出电流50 A，IGBT模块安装于水冷散热器，散热器足以消耗该模块全工况范围内的功耗，即IGBT器件壳温为室温25 ℃.由于Cauer热网络模型计算结果为芯片结温的平均值，因此，实验过程中，测取A，B，C3点的温度取平均值.红外热像仪测温，见图7a)，仿真与实验结果，见图7b).

图7 红外热像仪测温与仿真结果对比

由图7b)可知，仿真与实验结果基本吻合，验证了由Foster热网络模型转化为Cauer热网络模型的正确性.进而，基于该型IGBT器件验证后的模型，以其典型工况下的功率损耗与频率作为热网络模型的输入，见表3，对IGBT芯片结温及封装各层温度运行规律与作用关系进行了仿真研究.

表3 典型工况参数

该型IGBT器件各层在上述仿真条件下结温运行规律，见图8.

由图8可知，该模型可对IGBT器件各实际物理层温度进行仿真.芯片层、DBC层、基板层温度依次逐渐降低，温度波动范围逐渐减小，即所承受的热应力逐渐减小.因此，该模型计算结果可为IGBT器件各层材料与结构设计、封装各层失效分析提供依据.

图8 IGBT芯片、DBC、基板等效层温度运行规律

2 散热器传热模型参数设计方法

电力电子装置设计人员希望通过IGBT模块厂家提供的数据手册和装置的工况，以最快捷简便的方法完成IGBT器件的散热器设计.散热器的热阻、热容、散热方式决定了其散热性能，因此，设计合理的散热器即对上述参数进行优化.以一种大功率电力电子电能变换装置常用型号1 700 V/3 600 A IGBT模块为例，对IGBT模块散热器的设计方法进行了研究.

IGBT器件数据手册会提供Foster热网络结构的特征值，通过特征值即可计算出该网络结构下的热阻和热容，进而，采用Foster与Cauer热网络结构转换方法，将Foster网络结构转化为Cauer热网络结构，该型1 700 V/3 600 V IGBT模块的Cauer热网络结构与散热器参数，见图9.数据手册提供壳至散热器热阻为0.008 7 K/W，壳到散热器热容为500 J/K，常用散热器热阻为0.002 K/W.通过改变散热器热容，即可实现需求工况下的散热设计.

图9 热网络结构与散热器参数

采用Saber仿真平台对该模块不同散热器设计下的结温运行规律进行了仿真研究.仿真针对某型电力电子装置的典型工况开展，该工况下IGBT器件的损耗情况可等效为，周期3 s，占空比1/6，0～0.1 s损耗功率由0线性增大至4.5 kW，0.1～0.4 s为4.5 kW保持不变，0.4～0.5 s由4.5 kW线性增大至5 kW，随即装置停止工作2.5 s.单周期IGBT芯片损耗功率，见图10.

图10 IGBT单周期损耗功率

环境温度50 ℃，散热器热容5 000 J/K，仿真时长600 s时，单周期与多周期结温运行规律，见图11.

图11 IGBT模块单周期与多周期结温运行规律

由图11a)可知，在0～0.5 s内，结温依据损耗功率输入规律呈逐级增大趋势，最高温度达79.7 ℃.在0.5～3 s内，功率输入为零，结温从79.7 ℃呈指数规律下降.由图11b)可知，在0～200 s仿真时长内，结温由初始温度逐渐波动上升直至稳定.

在散热器不同热容设计、仿真时长600 s情况下，IGBT模块结温运行规律，见图12与表4.

由表4可知，IGBT芯片最高结温与波动范围随散热器热容的增大逐渐减小.当散热器热容为0.5，5，50 J/K时，IGBT芯片结温无温度累积效应.当散热器热容为500，5 000 J/K时，IGBT芯片结温有温度累积效应，且结温达到稳定的时间分别为30.5，222.5 s，即芯片结温达到稳态的时间随热容的增大而增大.依据上述方法、IGBT模块运行结温要求与散热器的散热方式，可对散热器进行合理设计.

表4 散热器不同热容设计结温信息

3 结 束 语

电力电子装置及组件热设计是保证其完成指定功能与可靠运行的重要环节.本文通过研究Foster热网络结构与Cauer热网络结构之间的转换方法，建立了一种IGBT模块封装结构传热模型参数等效计算方法，并对其各层结温运行规律进行了研究.通过研究散热器结构参数与结温之间的关系及规律，建立了一种散热器传热模型参数设计方法.为实现散热设计与可靠性分析奠定了基础.

[1]ENDER F, HANTOS G, SCHWEITZER D, et al. Thermal characterization of multichip structures[C]. Proc of Therminic,2013(2):319-322.

[2]EVANS P L, CASTELLAZZI A, JOHNSONAND C M. Automated fast extraction of compact thermal models for power electronic modules[J]. IEEE Transactions on Power Electronics,2013,28(10):4791-4802.

[3]WU R, WANG H, MA K, et al. A temperature-dependent thermal model of IGBT modules suitable for circuit-level simulations[C]. Proc of the IEEE Energy Conversion Congress and Exposition (ECCE),2014(6):2901-2908.

[4]MA K, BAHMAN A S, BECZKOWSKI S M, et al.Complete loss and thermal model of power semiconductors including device rating information[J]. IEEE Transactions on Power Electronics,2015,30(5):2556-2569.

[5]TANYA K G, BO T, JERRY L, et al. A real-time thermal model for monitoring of power semiconductor devices[J]. IEEE Transactions on Industry Applications,2015,51(4):3361-3367．

[6]KE M, MARCO L, FREDE B, et al. Thermal loading and lifetime estimation for power device considering mission profiles in wind power converter[J]. IEEE Transactions on Power Electronics,2015,30(2):590-602．

[7]任磊,韦徵,龚春英,等.电力电子电路功率器件故障特征参数提取技术综述[J].中国电机工程学报,2015,35(12):3089-3101.

[8]ZHAO H L, HYUNGKEUN A, MAHMOUD A, et al. A thermal model for insulated gate bipolar transistor module[J]. IEEE Transactions on Power Electronics,2004,19(4):902-907.

[9]TANYA K G, BO T, JERRY L, et al. A real-time thermal model for monitoring of power semiconductor devices[J]. IEEE Transactions on Industry applications,2015,51(4):3361-3367.

[10]KE M, MARCO L, FREDE B, et al. Thermal loading and lifetime estimation for power device considering mission profiles in wind power converter[J]. IEEE Transactions on Power Electronics,2015,30(2):590-602.

[11]KRISTIAN B P, KJELD P. Dynamic modeling method of electro-thermo-mechanical degradation in IGBT modules[J]. IEEE Transactions on Power Electronics,2016,31(2):975-986.

An Equivalent Parameter Calculation Method of IGBT Thermal Model

LIU Binli LUO Yifei WANG Bo MENG Qingyun ZHU Junjie

(NationalKeyLaboratoryofScienceandTechnologyonVesselIntegratedPowerSystem,NavalUniversityofEngineering,Wuhan430033,China)

Considering the power electronic equipment applications demanding for IGBT thermal characterization and design, an equivalent parameter calculation method of IGBT thermal model is established and verified experimentally, based on the properties and transformation methods between Foster and Cauer thermal network. The thermal characterization is studied, thus the temperature operation rule and interaction of each package layer are obtained. A design method of radiator thermal model is established, thus the laws of maximum junction temperature and fluctuation range with radiator capacitor are found.

structure of thermal network; equivalent calculation; operation rule of junction temperature; thermal design

2016-12-15

*国家自然科学基金项目(51490681、51507185)、国家重点基础研究发展计划(973计划)(2015CB251004)资助

TN607

10.3963/j.issn.2095-3844.2017.01.008

刘宾礼(1984—)：男，博士，助理研究员，主要研究领域为IGBT器件建模、健康状态监测与可靠性研究