基于几何特征的点到空间参数曲线最小距离的简化算法
2017-02-25马怡然郑志涛
马怡然郑志涛
(1.天津城建大学 天津 300384)
(2.中国特种设备检测研究院 北京 100029)
基于几何特征的点到空间参数曲线最小距离的简化算法
马怡然1郑志涛2
(1.天津城建大学 天津 300384)
(2.中国特种设备检测研究院 北京 100029)
分析了点到空间曲线的几何特征,根据这些几何特征,提出了点到空间参数曲线最小距离的简化算法。基于三次B样条曲线编制了计算机程序,通过大量算例验证了算法的有效性,其计算精度高,迭代速度快,程序执行效率高,在工程上具有一定的实用价值。
参数曲线 最小距离 迭代法 样条曲线
随着信息科技在传统制造业的深入和渗透,参数曲线和参数曲面由于优良的计算特性得到了广泛的应用。而求点到参数曲线的最小距离,是其中的一个基本问题,在游戏设计、机器人控制、数控加工等领域作为基本算法得到了广泛应用。在进行过山车仿真中,测得两条轨道线,如何把两条轨道线上点对应在一个轨道线法平面内并找出重心基准点,必须用点到曲线的最小距离,以一轨道曲线上点为基准,找到另一曲线上的最小距离点,即为对应轨道法平面上的点。科研人员[1-2]采用多种方法计算点到空间参数曲线的距离,但这些算法多集中讨论如何求点到一个节点区间的最小距离方法,如何求点到多个节点控制的整条参数曲线的最小距离目前未见有详细研究方法。本文以常用的双三次B样条曲线为例,研究了快速实用的点到空间参数曲线最小距离的算法。
1 点到空间参数曲线最小距离的数学模型
对于空间参数曲线Γ,其参数方程为:
也可以表示为参数u的矢函数:
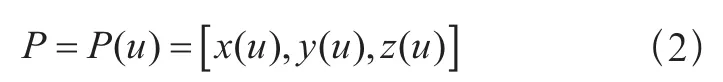
空间曲线是一维的,因此只有一个参数u,且0≤u≤1。对于不同的参数曲线,如贝塞尔曲线、B样条曲线或非均匀有理B样条曲线,P(u)具有不同的表达形式,可以根据实际情况来确定。
设给定点Q(x0,y0,z0),它到空间曲线给定点P(x(u), y(u),z(u))的距离可表示为

则最小距离可表示为:

对以上方程用搜索法求解,编程比较麻烦,以下从点到曲线最小距离的几何特征入手,提出另一种解题思路。
2 点到曲线最小距离几何特征分析
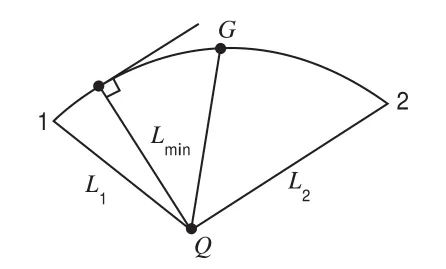
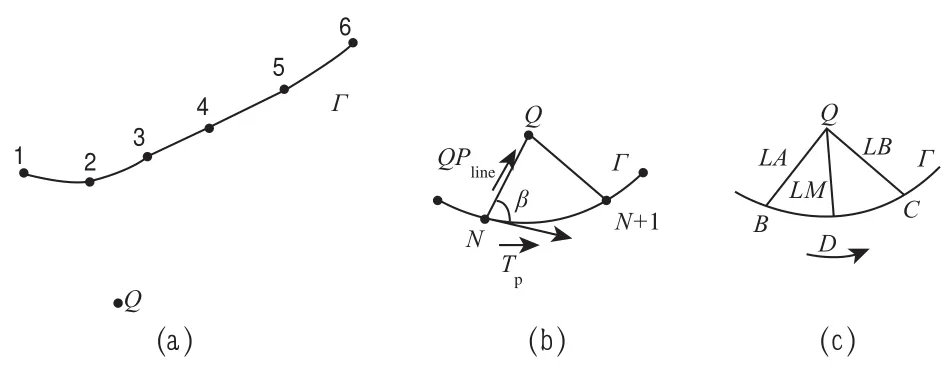
1)如图1所示: L1>L2>Lmin,Lmin 图1 点到曲线最小距离点所在区间 图2 点到曲线的最小距离 3)对于给定点Q,若QM与M点的切线MT所夹角分别为α与β,设α>β,则最小距离点P必位于β角一侧,如图3所示。 图3 4)对于节点内一段曲线,如果存在最小距离点,如图4平分该段曲线,中点为G,若L1<L2,则垂足必位于L1侧,即最小距离点必位于L1侧(适用于Q到曲线各点距离小于各点曲率半径的曲线)。 图4 对于如图5所示点Q和样条曲线Γ,基于几何特征的点到空间参数曲线最小距离的计算步骤为: 图5 1)计算给定点Q到样条曲线Γ各节点的距离; 2)比较Q到样条曲线Γ各节点的距离,根据以上原理1,则最小距离点必位于最短节点距离QN线两侧的相邻曲线段上,如图5(b)所示; 3)由QN与N点切线 所夹角度,根据以上原理3,判断出最小距离点必位于锐角一侧所在的相邻弧段; 4)取该弧段内中点D,比较给定点Q与B、C两点的距离,如图5(c)所示,根据以上原理4,则最小距离点必位于距离短的端点所在的半个区间; 5)舍弃不存在最小距离点的一半区间,再取另一半区间中点,重复以上过程4),直到两边差值小于给定ε(即 |Ln-Ln+1|<ε),则该边长LM即为所求最小距离,D点即为最小距离点。 在工程实际中常应用双三次B样条曲线来表示以上曲线,其参数矩阵表达式为: 式中bi(i=0,1,2,3)为双三次B样条曲线的控制点矢量,则: 利用三次B样条曲线,做出求最小距离点的流程图如图6所示: 图6 三次B样条曲线法求最小距离点的流程图 表1为三次B样条曲线的节点,曲线外给定点为Q(49428.1937,-16671.1419,3445.0020),采用基于几何特征的点到空间参数曲线最小距离的算法,程序仅迭代7次即找出最小距离1220。 表1 三次B样条曲线节点数据 采用搜索法求解,至少要17步以上方能求出符合要求的点,而且随着曲线点数的增加,计算迭代数量相应增加,运算量会线性增加,程序执行效率则会降低。 利用以上点到空间曲线最小距离处的几何特征求取最小距离,具有编程简单,程序迭代次数小,执行效率高,是求最小距离的一种简便方法。以上方法对曲线曲率变化相对平缓时适用,对曲线上存在拐点的曲线不适用。 [1] 伍丽峰,陈岳坪,谌炎辉,等.求点到空间参数曲线最小距离的几种算法[J].机械设计与制造,2011,9:15-17. [2] 钱春.基于区间牛顿法的点到参数曲线最小距离的计算方法[J].机电工程,2010,27(1):82-84. [3] 廖平.分割逼近法快速求解点到复杂平面曲线最小距离[J].计算机工程与应用,2009,45(10):163-164. A Simplifed Algorithm of the Minimum Distance Between a Point and a Spatial Parametric Cure base on the Geometrical Characteristic Ma Yiran1Zheng Zhitao2 This paper analyzes the geometric characteristics between a point and a spatial parametric cure, based on which a simplified algorithm of the minimum distance between a point and a spatial parametric cure is developed. Based on the cubic spline curve, the programs is designed. The effectiveness, high precision, quick iteration and high effciency of the algorithms are verifed by a series of tests. It has more practical value in engineering practice. Parametric curve Minimum distance Iteration method Spline X924 B 1673-257X(2017)01-0029-03 10.3969/j.issn.1673-257X.2017.01.006 马怡然(1978~),女,硕士,讲师,从事工科数学及研究工作。 2016-09-07)


3 点到曲线最小距离算法设计
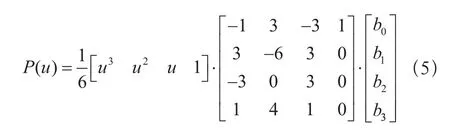

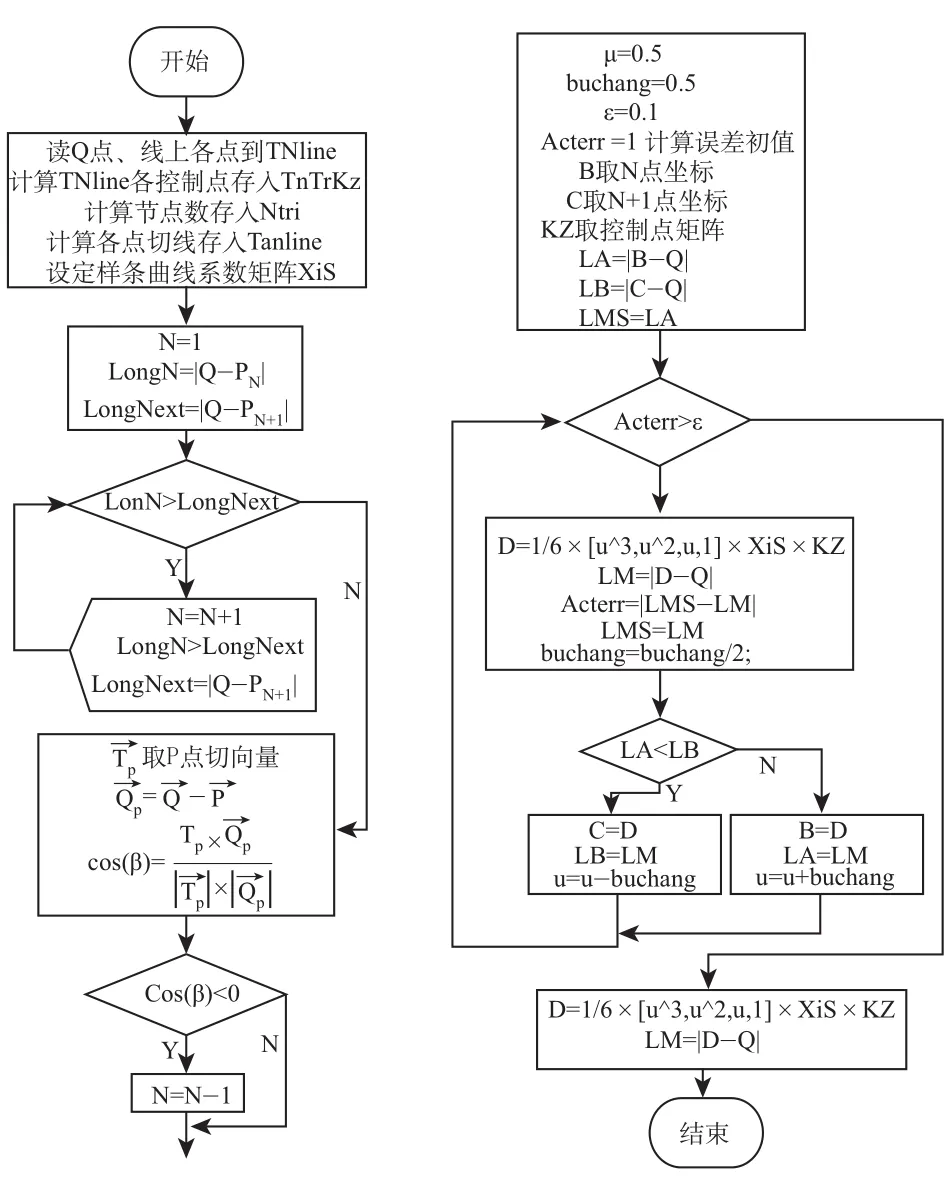
4 实例分析

5 结论
(1. Tianjin Chengjian University Tianjin 300384)
(2. China Special Equipment Inspection and Research Institute Beijing 100029)
