一种基于GSC的自适应和差测角方法

孔永飞，吴海洲

(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

一种基于GSC的自适应和差测角方法

孔永飞，吴海洲

(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

在阵列信号处理中，通常利用和差波束估计目标角度，存在干扰时自适应波束形成在干扰方向形成零陷、和差波束的主瓣方向图产生畸变、和差波束比与普通波束形成存在偏差、角度估计结果误差较大等问题。为解决上述问题，开展了无需校正的自适应和差波束测角研究，提出一种基于广义旁瓣相消器的和差波束双通道结构，该结构可以在抑制干扰的同时保持主瓣波束方向图，角度估计结果精度高。仿真结果表明，提出的方法在有效抑制干扰的同时，保持了良好的单脉冲特性。

GSC；自适应和差波束；鉴角曲线

0 引言

在自适应阵列信号处理中，应用和差波束测角技术[1]时，如何在抑制干扰的同时减轻对和差波束主瓣方向图的影响[2]，获得良好的鉴角曲线，是一个值得研究的课题。

广义旁瓣相消器(Generalized Side-lobe Canceller，GSC)的自适应干扰对消思想基于维纳滤波原理，通过抵消上、下支路中的相关干扰和噪声，输出的误差信号即为期望信号。文献[3]提出一种快速自适应和差测角方法，基于GSC结构形成和差波束，其自适应辅助支路未做降维处理，运算复杂度较高。文献[4]提出一种基于GSC结构的三通道自适应和差测角方法，在自适应辅助支路中，采用多级维纳滤波器构造降维阻塞矩阵，方法复杂，运算量较大。

本文提出一种基于GSC的和差波束双通道结构，在自适应辅助支路中，构造稳健降维阻塞矩阵，在保持和差波束主瓣方向图的基础上，形成干扰方向的零陷，应用对称取反法[5]，利用和差波束估计目标角度。

1 对称取反法

在N元线阵应用和差测角技术时，采用对称取反法，将所有阵元等分为2个子阵，和波束通道与差波束通道的构成如图1所示。

对应的和与差操作矢量如下：

利用和差操作矢量，得到普通波束形成和波束权矢量w∑及差波束权矢量wΔ:

w∑=a(θ0)○T∑,wΔ=a(θ0)○TΔ。

式中，θ0为波束指向角；○表示Hadamard乘积。

偏角Δθ的计算公式为：

式中，L0为子阵相位中心到对称轴的距离。

图1 和差波束构成示意

2 和差波束的GSC结构

基于GSC的和差波束双通道结构如图2所示，由2个并行的GSC构成，上GSC结构对应和波束通道，下GSC结构对应差波束通道。经GSC上下支路变换后，进入维纳滤波器，通过抵消上、下支路中的相关干扰和噪声，输出的误差信号即为和波束信号和差波束信号。

图2 基于GSC的和差波束双通道结构

和与差通道GSC权矢量如下：

(1)

在实际阵列应用中，为了减小由于通道误差[6]造成的信号相消现象，对阻塞矩阵加以改进，通常把期望信号的理想导向矢量向信号子空间做投影[7]，利用投影导向矢量构成的降维阻塞矩阵比直接利用理想导向矢量构成的降维阻塞矩阵有更好的阻塞能力。

采用信号子空间和噪声子空间特征向量的线性组合构造的阻塞矩阵BN×J，其中N表示阵元个数，J表示阻塞矩阵维数，只有当J=M-1时，M为目标信号个数与干扰信号个数之和，抗干扰后的和差波束主波束畸变较小，才能用于和差波束测角，现简要分析如下：

当J=N-1时，阻塞矩阵为：

B=[b1b2…bN-1]N×(N-1)。

(2)

GSC结构权矢量一般形式如下：

(3)

(4)

又有

(5)

(6)

(7)

把式(7)代入式(3)，得到

(8)

由于子空间投影导向矢量ap与噪声特征矢量矩阵En正交，可得

(9)

将式(9)代入式(8)，有

(10)

由此可得，在GSC结构中，自适应辅助支路采用N-1列稳健阻塞矩阵时，结果与稳健LCMV方法等效，由于稳健LCMV方法对指向误差不敏感[8]，主瓣波束始终指向实际信号方向，不能用于和差波束角度估计。

实际上，在GSC结构中，白噪声不可抵消，自适应辅助支路中只需包含干扰信号分量[9]，即利用信号子空间特征矢量的线性组合构造稳健降维阻塞矩阵BN×(M-1)，M由估计[10]得到，阻塞噪声和期望信号，辅助支路只允许干扰信号通过，有效提高输出信号的信干噪比，此时，自适应和方向图可表示如下：

(11)

当a(θ)=a(θ0)时，由于B满足

(12)

且B为信号子空间一组正交基的线性组合，满足

(13)

由式(12)和式(13)，可得

(14)

把式(14)代入式(11)，当θ=θ0时，自适应和方向图幅值为：

(15)

说明在θ0处的自适应波束形成方向图与普通波束形成方向图相同，且当θ在θ0附近时，a(θ)≈a(θ0)，BHa(θ)近似为0，主要是aH(θ0)a(θ)起作用，即自适应和波束形成在θ0附近接近于普通和波束形成。

自适应差方向图可表示为：

(16)

式中，aH(θ0)为静态差波束权矢量。同上，当θ=θ0时，有

(17)

同上，自适应差波束形成在θ0附近接近于普通差波束形成。

3 仿真验证

以均匀线阵为例，阵元数N=32，阵元间距半波长，来波信号为远场窄带信号，且各信号互不相关，噪声与来波信号也不相关。假定期望信号来自10°方位，信噪比为0dB，2个干扰信号分别来自40°和-10°，干噪比分别为30dB和20dB。

3.1 自适应和差波束方向图

初始波束指向为11°，采样点数为512，和差波束方向图如图3和图4所示。

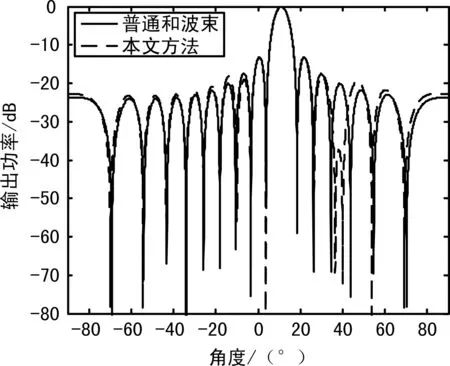
图3 和波束方向图

图4 差波束方向图

图3是所提方法的自适应和波束方向图与普通和波束形成方向图，所提方法在干扰方向40°和-10°形成零陷，在40°方向零深-72.21dB，-10°方向零深-56.06dB，能有效地消除干扰。

图4是所提算法的自适应差波束方向图与普通差波束形成方向图，所提方法在干扰方向40°和-10°形成零陷，在40°方向零深-61.35dB，-10°方向零深-63.37dB，能有效地消除干扰。

由图3和图4可知，本文所提方法形成的自适应和差波束的主瓣波束指向与普通波束的主瓣波束指向相同，同时有效抑制干扰。

所提方法的自适应单脉冲比曲线与普通和差波束的单脉冲比曲线如图5所示。所提方法的单脉冲比曲线与静态单脉冲比曲线十分接近，无需修正，利用该鉴角曲线得出角度估计结果为9.95°。

图5 鉴角曲线

3.2 测角精度

其他仿真参数不变，采样点数从256增加到4 096，分别做100次MonteCarlo实验，角度估计结果如表1所示。

表1 不同采样点数时角度估计结果

从表1可见，随着采样点数的增加，阵列协方差矩阵估计趋于理论值，所提方法测角结果均方根逐步减小，测角结果稳定性增高，相对于期望信号真实角度10°，即便在采样点数较低时，误差在0.2°以内，相对于主瓣波束宽度6.35°，误差小于3.2%，随着采样点数的提高，误差趋于1%，表明所提方法测角精度较高，无需修正鉴角曲线。

4 结束语

本文提出一种基于GSC结构的自适应和差波束形成的方法，可以在形成和差波束的同时在干扰方向形成零陷，得到良好的和差波束鉴角曲线，与普通和差波束鉴角曲线十分接近，测角精度较高，同时大大减少了GSC结构辅助支路自适应权的维数，降低了系统的运算量，在工程实践中具有比较好的应用前景。仿真试验及性能分析都验证了算法的有效性和优越性。

[1] 胡体玲，李兴国.单脉冲探测技术的发展综述[J].现代雷达，2006，28(12)：24-29．

[2] 廖 晖，黄忠平.基于方向图保形的单脉冲测角算法[J].中国电子科学研究院学报，2010，5(3)：301-304.

[3]MOONSH,HANDS,CHOMJ,etal.ANewGSCUsingMonopulseAngleEstimationTechniqueforFastTargetTracking[C]∥IEEEInternationalSymposiumonPhasedArraySystemsandTechnology,2003:158-163.

[4]HEYD,ZHOUJ,ZHOUBH.AdaptiveSumandDifferenceBeamformingforMonopulseSystemwithArrayAntennas[C]∥ 6thInternationalConferenceonWirelessCommunicationsNetworkingandMobileComputing(WiCOM),2010:1-5.

[5] 曾 操，陈 昊.相控阵子阵级和差多波束测角方法[J].西安电子科技大学学报，2007，5(3)：213-219.

[6] 见 伟，张 玉，韩名权.阵列天线通道误差对波束性能的影响分析[J].无线电工程，2014，44(11)：45-48.

[7] 张涛麟，廖桂生，曾 操.基于广义旁瓣相消的新降维方法[J].雷达科学与技术，2007，5(3)：213-219.

[8]FELDMANDD,GRIFFITHSLJ.AProjectionApprochforRobustAdaptiveBeamforming[J].IEEETransactionsonSignalProcessing,1994,42(4):867-876.

[9]VANVEENBD.EigenstructureBasedPartiallyAdaptiveArrayDesign[J].IEEETransactionsonAntennasandPropagation,1988,36(3):357-362.

[10] 贡彦飞.基于盖尔圆准则的信源个数估计算法比较[J].无线电通信技术，2012，38(4)：57-59.

孔永飞 男，(1987—)，硕士，工程师。主要研究方向：航天测控、阵列信号处理。

吴海洲 男，(1977—)，博士，高级工程师。主要研究方向：航天测控、阵列信号处理。

An Angle Estimation Method by Adaptive Sum and Difference Beam-forming Based on GSC

KONG Yong-fei,WU Hai-zhou

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

In array signal processing,the angle of target is usually estimated by applying sum and difference beam-forming.Adaptive beam-forming distorts the sum and difference main lobe patterns,resulting in difference between the adaptive sum-difference ratio curve and the common sum-difference ratio curve,which leads to serious angle estimation error.An angle estimation algorithm without correction based on sum and difference beam-forming is proposed to solve the above problem.The proposed algorithm is based on the GSC structure of sum and difference channels,and has effective jamming suppression and high performance of angle estimation with less impact on sum-difference ratio.Simulation results demonstrate that the proposed algorithm can suppress jamming effectively,while preserving good monopulse performance.

GSC;adaptive sum and difference beam-forming;monopulse response curve

10.3969/j.issn.1003-3106.2017.01.09

孔永飞,吴海洲.一种基于GSC的自适应和差测角方法[J].无线电工程,2017,47(1):36-39.

2016-11-08

国家高技术研究发展计划(“863”计划)基金资助项目(2013AA122105)。

TTN911

A

1003-3106(2017)01-0036-04