基于改进的近邻传播聚类算法的Gap统计研究

唐 丹,张正军,王俐莉

(1.南京理工大学 理学院 统计与金融数学系,江苏 南京 210094;2.海军指挥学院科研部,江苏 南京 210016)

基于改进的近邻传播聚类算法的Gap统计研究

唐 丹1,张正军1,王俐莉2

(1.南京理工大学 理学院 统计与金融数学系,江苏 南京 210094;2.海军指挥学院科研部,江苏 南京 210016)

由于K-means算法初始聚类中心的选取具有随机性，聚类结果可能不稳定，导致Gap统计估计的聚类数也可能不稳定。针对这些不足，提出一种改进的近邻传播算法-mAP。该算法考察数据的全局分布特性，不同的点赋予不同的P值。在Gap统计中用mAP算法代替K-means算法,提出基于mAP的Gap统计mAPGap。mAP能在较短的时间内得到较好的聚类效果，而且不需要预先设定初始聚类中心，聚类结果更稳定。实验结果表明,mAPGap在估计聚类数的稳定性和聚类精度上都优于原Gap。

聚类分析;近邻传播聚类;偏向参数;K-means算法;Gap统计

0 引 言

数据集的聚类数估计是数据分析中的一项重要课题。2000年，R.Tibshirani等提出确定最佳聚类数的Gap统计量[1]，采用的聚类算法是K-means算法，该算法需要选取初始聚类中心，通常随机选取K个样本点作为初始聚类中心。2013年，刘倩基于Gap统计方法研究了K-means算法，提出了一种基于数据分布规律具有自适应特点的DSA-K-means算法[2]。2013年，陆琴琴针对基于矩Gap统计的图像分割算法中K-means算法存在的缺陷，提出了MMGSK算法[3]。

2007年，Frey[4]和MezardM[5]提出了属于划分聚类方法的近邻传播(AffinityPropagation,AP)算法。该算法具有如下优点：能在较短时间内得到较好的聚类效果[6]；算法中类代表点是原始数据中的点，而不是数据的均值点；以误差平方和作为衡量算法优劣程度的准则函数时，算法聚类的误差平方和显著低于其他方法聚类的误差平方和。但是AP算法对偏向参数P的设定，没有考虑数据的分布结构，认为所有数据点成为类代表点的可能性相同。

文中提出了利用全局数据信息设置偏向参数P的改进的AP算法-mAP(modifiedAffinityPropagation)，同时提出了自适应的增加步长，得到数据集的聚类数，运用Gap统计量估计出该数据集的合理聚类数。

1 mAP模型

AP是一种基于近邻信息传播的聚类算法，根据N个数据点之间的相似度进行聚类[7]。这些相似度组成N×N的相似度矩阵S。S矩阵的对角线上的数值s(k,k)称为偏向参数preference,记作P,表示数据点k作为类代表点的适合程度。该值越大，k点成为类代表点的可能性也越大,同时得到的聚类数越多[8]。AP算法中传递两种类型的消息，即归属度a(i,j)和吸引度r(i,j)，前者表示xi选择xj作为类代表的合适程度，后者表示xi对xj作为类代表点的支持程度[9]。AP算法通过迭代过程不断更新每一个点的吸引度和归属度值，直到迭代过程收敛，类代表也随之固定，同时将其余的数据点分配到相应的聚类中[10]。

传统的AP算法中相似度矩阵对角线上的偏向参数P是相同的，一般取所有相似度的中值(median(s(:,3))，意味着数据点在开始时被选择作为类代表点的概率是相同的。但是，P值的这种初始设置方法是不科学、不精确的，因为它忽略了数据点结构的差异对某点成为类代表点的可能性的影响。类代表点的选择与点的位置密切相关：对给定的数据集X和点xi,xj，如果xi是边缘数据点而xj是中心数据点，那么从其他点到xi的距离和大于到xj的距离和，xj成为类代表的可能性要大于xi。

针对如上假设，文中提出基于全局数据点设置P的值，同时为了获得不同的聚类数，提出一种自适应设置步长获得不同聚类数的方法。具体步骤如下：

(1)对任意点xi，计算从其他所有点到xi的相似度之和：

(1)

(2)

(3)对AP算法设置步长，获得不同聚类数。

根据上述讨论可知，当每个数据点的P值相同时，聚类数随P值的增大而增大。所以为了得到不同的聚类数，P存在取值区间[Pmin,Pmax]。WangCD[11]通过研究得到:

(3)

由于AP算法每个点的P值相同，可以通过下式获得：

(4)

其中，Npref是输入参数，表示设置Npref个不同P。

(4)对mAP算法设置步长，获得不同聚类数。

对i=1,2,…,n(n代表样本点个数)，有：

(5)

(6)

其中

(7)

由于对每个点的PiMin都是Pmin乘以一个权重，所以会使得每个点的初始P值变小。为了确保能够取到1～maxK类，这里把Pmin取得更小，是用相似度矩阵元素的最小值乘以样本点个数n。

对于连续的k，mAP算法得到的分类情况会大量重复。文中根据mAP算法的聚类结果动态计算步长，在不改变结果的基础上优化了算法的运行时间。

2 mAP算法

s(i,k)=-‖xi-xk‖,i≠k

(8)

(2)对于每一个Npref，根据式(5)～(7)计算每个点的偏向参数，能得到Npref个1*n数组。

(3)消息传递。

①更新吸引度矩阵r(i,k)和归属度矩阵a(i,k)。

r(i,k)=s(i,k)-max{a(i,k')+s(i,k')}(k'≠k)

(9)

(10)

(11)

②引入阻尼系数λ，消除可能出现的震荡。

(12)

其中，λ(0<λ<1)越大越能消除震荡，但会减缓算法收敛的速度。

(4)循环执行步骤(3),直到满足终止条件。终止条件为达到最大迭代次数maxits或聚类划分连续Convits次不变。

(5)输出聚类结果。输出Npref组类代表点及其对应的数据点划分。

3 mAPGap模型(Gap Statistic Based on mAP)

原Gap统计方法的主要思想是：选择一个参考分布，将待分类数据的离散程度与由参考分布生成数据集的离散程度进行比较，以分类数为自变量，建立一个比较统计量，通过分析该统计量关于类数的变化情况确定最佳聚类数[12]。

原Gap统计的主要内容是：假设数据是通过K-means算法已被聚为k类:C1,C2,…,Ck，nr=|Cr|。令：

(13)

其中，Dr表示聚类r中所有数据两两之间的距离平方之和。

再令：

(14)

其中，Wk表示k类离差程度的总和。

由此定义Gap统计量：

(15)

为了区分基于不同算法的Gap统计，这里把基于K-means算法的原Gap统计记作KMGap。

由于KMGap统计需要预先生成大量的参考数据集，因而不适宜通过mAP算法实现不同类数的聚类，而且参考数据集类内离差程度是均匀分布下大量数据集类内离差程度的期望，根据Khinchin大数定律[14]知，使用K-means算法聚类能够保证结果的稳定性。鉴于以上两点，对参考数据集的聚类方法仍使用K-means算法。

使用mAP算法对样本数据集进行聚类，当选择负的欧氏距离作为两个样本点的相似度时，mAP算法的准则函数也即是使每个样本点到其类代表点的平方距离之和最小，这与K-means算法的准则函数一致。因此使用mAP算法对样本数据集进行聚类，使用K-means算法对参考数据集进行聚类，再利用Gap统计量估计该数据集的聚类数是合理的。

mAPGap的计算可分为以下3步:

(1)利用mAP算法，将样本数据集聚集为k(k=1,2,…,K)类，计算Wk(在偏向参数不同时会出现相同的分类数k，这里Wk取它们的平均值)。

(16)

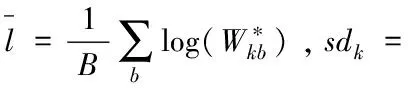
Gap(k)≥Gap(k+1)-sk+1

(17)

4 仿真实验与分析

文中实验采用MATLAB7.0开发环境，在Windows7操作系统的计算机上运行通过。

4.1 实验数据集

表1 实验数据集描述

4.2 实验评价标准

实验采用3种评价指标对聚类结果进行评价：

(1)对三个数据集,分别利用KMGap、APGap、mAPGap重复运行20次，估计出最佳聚类数的正确率p。

(2)算法运行时间t。虽然AP算法复杂度为O(N*N*logN)，而K-means的是O(N*K)，但当样本容量不是非常大时，两者时间相近。故这里对具体数据集的运行时间进行比较。

(3)聚类精度。定义为：

(18)

其中，TC为正确聚类的数据数；FC为错误聚类的数据数。

由于AP算法和mAP算法都会出现在估计的最佳聚类数相同时，具体的聚类结构不同的情况，所以对某个特定的聚类，聚类精度有不同的值。结果分析中，AP算法和mAP算法的精度记录的都是最小值。当最小值都优于KMGap时，说明APGap算法和mAPGap算法聚类的精度优于KMGap。

4.3 结果与分析

对三个数据集分别执行KMGap、APGap、mAPGap聚类，聚类结果及性能如图1、表2所示(由于版面有限，这里只给出Haberman的聚类结果)。

图1 Haberman数据集中的KMGap、APGap、mAPGap随类数k的变化曲线

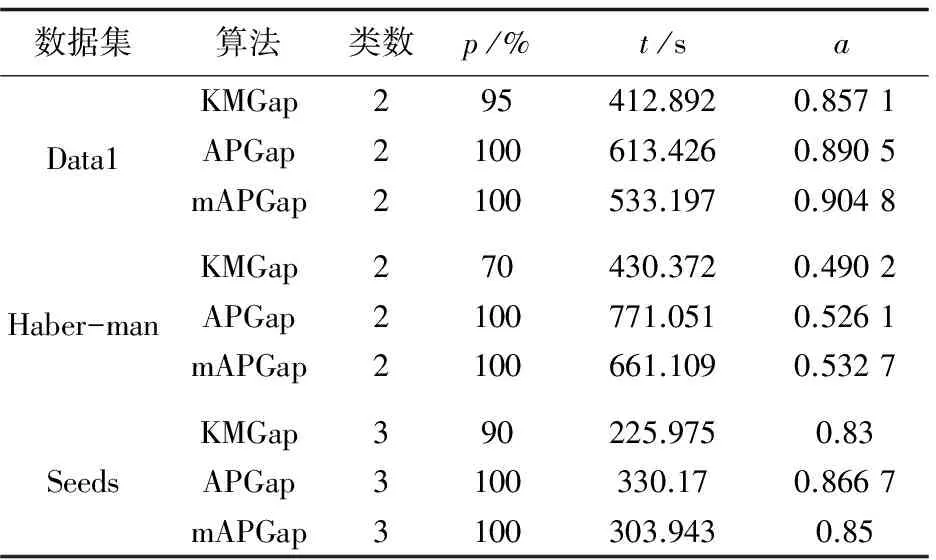
数据集算法类数p/%t/saData1KMGap295412．8920．8571APGap2100613．4260．8905mAPGap2100533．1970．9048Haber-manKMGap270430．3720．4902APGap2100771．0510．5261mAPGap2100661．1090．5327SeedsKMGap390225．9750．83APGap3100330．170．8667mAPGap3100303．9430．85

实验结果表明，相比于KMGap，APGap、mAPGap

虽然运行时间增加了一点，但二者具有很好的稳定性，同时二者均可以提高分类精度。而且mAPGap与APGap相比，在不影响稳定性和精度的情况下，减少了算法运行时间。总体来说，mAPGap算法优势明显的原因是：利用数据结构设置每个数据点的偏向参数，减少了算法运行时间；不需要预先设定初始聚类中心和聚类数，使得聚类结果更稳定，精度更高。

5 结束语

文中提出根据数据的全局分布特性设置偏向参数P的AP算法(mAP),在Gap统计中，用mAP算法替换K-means算法，提出基于mAP的Gap统计量(mAPGap)。通过实验证明了mAPGap在聚类结果的稳定性，并且在精度上要优于原算法。

[1]TibshiraniR,WaltherG,HastieT.Estimatigthenumberofclusterinadatasetviathegapstatistic[J].JournaloftheRoyalStatisticalSociety,2001,63(2):411-423.

[2] 刘 倩.基于GS方法的图像分割估计数的多信息动态研究[D].南京:南京理工大学,2013.

[3] 陆琴琴.基于矩Gap统计的图像分割方法[D].南京:南京理工大学,2014.

[4]FreyBJ,DueckD.Clusteringbypassingmessagesbetweendatapoints[J].Science,2007,315(5814):972-976.

[5]MezardM.Wherearetheexamplars?[J].Science,2007,315(5814):949-951.

[6] 冯晓磊,于洪涛.密度不敏感的近邻传播聚类算法研究[J].计算机工程,2012,38(2):159-162.

[7] 邢 艳，周 勇.基于互近邻一致性的近邻传播算法[J].计算机应用研究,2012,29(7):2524-2526.

[8] 段丽莉.改进的近邻传播算法及其在图像处理中的应用[D].西安:西安电子科技大学,2014.

[9] 邢长征，刘 剑.基于近邻传播与密度相融合的进化数据流聚类算法[J].计算机应用,2015,35(7):1927-1932.

[10] 肖 宇，于 剑.基于近邻传播算法的半监督聚类[J].软件学报,2008,19(11):2803-2813.

[11]WangCD,LaiJH,SuenCY,etal.Multi-exemplaraffinitypropagation[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2013,35(9):2223-2237.

[12] 童 波.基于MFGS方法图像最佳分隔数的研究[D].南京:南京理工大学,2011.

[13] 黄陈蓉,张正军,吴慧中.图像边缘检测的多尺度灰度Gap统计模型[J].中国图象图形学报,2005,10(8):1018-1023.

[14] 冯 予,陈 萍.概率论与数理统计[M].第2版.北京：国防工业出版社,2015:114-117.

Study on Gap Statistic Based on Modified Affinity Propagation Clustering

TANG Dan1,ZHANG Zheng-jun1,WANG Li-li2

(1.Department of Statistic and Financial Mathematics,College of Science,Nanjing University of Science and Technology,Nanjing 210094,China; 2.Scientific Research Department of Naval Command College,Nanjing 210016,China)

Due to the randomness of choosing the initial clustering ofK-meansmethod,itmaycausetheinstabilityofclusteringresultsandthenleadtothatofclusteringnumberswhichareestimatedbyGapstatistic.Takingconsiderationofthosedisadvantages,anmodifiedAPclustering(mAP)ispresentedwhichutilizestheglobaldistributiontogivedifferentPtodifferentpoints.mAPmethodisputforwardtosubstitutetheK-meansinGapstatisticnamedmAPGap.mAPmethodhasmorestableclusteringcenterbecausetheinitialclusteringcenterandnumbersarenotneededinadvanceanditcangetbetterclusteringinshorttime.TheexperimentalresultsdemonstratemAPGapissuperiortoGapinclusteringstabilityandaccuracy.

cluster analysis;affinity propagation clustering;preference;K-meansalgorithm；Gapstatistic

2016-03-15

2016-06-22

时间：2017-01-04

全国统计科学研究计划重点项目(2013LZ45)

唐 丹(1990-),女,硕士研究生,研究方向为数据分析与数据挖掘;张正军,博士,副教授,研究方向为数据分析与数据挖掘、马尔可夫链理论与方法等。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1102.086.html

TP

A

1673-629X(2017)01-0182-04

10.3969/j.issn.1673-629X.2017.01.041