基于VOO方法的云计算平台多目标任务调度算法

朱丽玲，杨智应

(上海海事大学 信息工程学院，上海 201306)

基于VOO方法的云计算平台多目标任务调度算法

朱丽玲，杨智应

(上海海事大学 信息工程学院，上海 201306)

目前，云计算正不断兴起和发展,它作为一种新的技术和商业模式受到国内外学者的重视。而任务调度问题是云计算的核心问题之一，也是研究热点。针对云计算中的任务调度问题，以完成时间和货币成本作为任务调度的两个性能指标，基于POSH算法，主要采用序优化的方法对任务调度问题的解集进行优化，获得一个相对最优的解。实验中将多HEFT算法和POSH算法进行了对比，结果表明，提出的方法在完成时间波动相对小的情况下，能够降低货币成本。因此，所提出的算法是有效的。

云计算；向量序优化；任务调度；多目标；完成时间；货币成本

0 引 言

云计算是在分布式计算、并行计算、网格计算的基础上发展起来的，其最大的特点就在于“按需使用，按量付费”[1]。云计算通过大规模的数据中心，为用户提供强大的计算能力、海量的数据存储能力，并且比一般的数据中心更加节能、经济和高效。而如何合理分配计算资源，现已成为云计算领域的热点研究内容之一。任务调度作为云计算中的核心技术，如何在网络带宽、CPU、存储受到限制的情况下高效使用有限的资源，是云计算系统中亟须解决的一个关键性技术难题。

目前，云计算平台下的工作流调度问题是一个众所周知的NP-难问题，难点就在于如何适应多个目标，而且这些目标之间可能存在相互竞争关系。例如，如何在任务完成时间最小化的前提下，使得资源花费最小，保证容错率或是服务质量(QoS)。国内外学者就这方面作了大量研究。李剑锋等[2]提出了一种具有双适应度的遗传算法，主要运用于云计算的编程模型框架MapReduce，该算法是基于任务总完成时间和任务的平均完成时间这两个性能指标进行优化的。华夏渝等[3]通过分析带宽、响应时间等影响因素，提出了一种基于种群优化的计算资源分配方式，能够使其获得更短的响应时间和更好的运行质量。He等[4]针对Min-Min算法进行改进，根据用户是否有QoS的需求对系统吞吐量进行优化。Johan T等[5]提出了一种基于粒子群优化的调度算法，充分考虑了任务调度的总完成时间和成本。Kong等[6]以时间和可靠性为性能指标，以模糊规则为预测模型，提出了基于模糊预测的有效的任务调度方法。Su等[7]提出POSH算法，将完成时间和成本这两个目标转换成单目标，获得一个满足完成时间与成本相对满意的策略，但往往可能会陷入局部最优的问题。

以上提出的方法，在执行大程序的情况下，任务调度的策略空间集合将会变得非常庞大，那么想要获得一个相对满意的任务调度策略，其计算的成本也会随之上升。因此，文中在对云计算环境下的任务调度的新特性以及任务调度算法的研究现状和相关研究成果进行归纳总结的基础上，基于文献[7]中的启发式算法POSH，采用序优化方法对任务调度策略集进行优化，并基于该集合获得一个相对最优解。

1 问题模型

假设一个工作流调度系统有S个虚拟集群，虚拟集群中的虚拟节点数可以由mi(i=1,2,…,S)表示，使用W个工作流管理者将任务分配到各个集群的相应队列，控制作业的进程，如图1所示。每个集群对应一个队列，W个控制管理器管理S个队列。

图1 云平台虚拟机资源分配模型

总结了基本标识及其含义，i表示虚拟集群i，k表示存在k任务集。简单来说，描述的是一个双目标模型，该模型是为了最小化任务的执行时间和资源操作成本。最优化指标J1和J2分别表示每个任务集时间tk的总和的最小值和资源总耗费的最小值。这两个目标函数和约束条件将在下文定义，共同构成调度模型[8]。

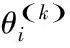
目标函数：

(1)

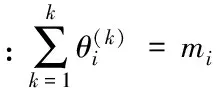
类似地，如果存在N个优化指标，那么就需要定义N个目标函数。

2 VOO仿真优化方法

序优化[9](Ordinal Optimization,OO)方法是解决仿真优化的一个重要工具，该方法经常用于类似多工作流调度的问题，且任务调度策略空间异常庞大的情况下。序优化最重要的原则是“序与值”，通俗来讲就是序的比较往往比值的比较容易得多。序优化的方法是建立在粗糙模型的基础上，不足以精确地判断出任意两个解之间性能差别是多少，但是能够精确地判断出两个解到底孰优孰劣。

文中研究的任务调度算法是基于两个性能指标，分别是完成时间和货币成本。解决多目标的优化问题，需要采用向量序优化(Vectorized Ordinal Optimization,VOO)方法，即序优化方法的延伸，也就是将标量的情形推广到向量的情形。向量序优化方法与序优化之间存在一定的差异，主要体现在以下几个方面：

(3)足够好的解。真实模型下的前g层可作为足够好的解的集合G。

(5)向量性能曲线图(VectorOrderedPerformanceCurve,VOPC)。这个概念主要是用于描述由粗略模型产生的解的排列情况。具体如图2所示,一般分为平坦型、中间型和陡峭型，显然陡峭型更能获得最优解。

(6)噪声级别(NoiseLevel)。该概念的提出主要是为了描述粗略模型与真实模型之间的误差，可以通过计算粗略模型估计出真实模型。

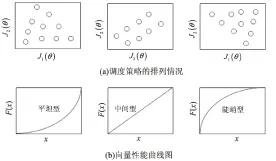
图2 双目标优化问题的策略排列以

云平台上的多目标调度问题是一个众所周知的NP难问题。基于以上论述，可以了解到向量序优化的方法适用于文中的双目标调度问题，根据传统调度算法一次只能获得一个任务调度策略，而无法预知策略是否最优，那么可以进行多次试验获得大量的任务调度策略，并在此基础上采用向量序优化的方法在任务调度策略集中获得一个相对最优的解，这样不仅可以避免陷入局部最优的问题，而且也能大大提高任务调度的效率。

下面总结向量序优化的一般步骤：

(1)根据平均采样的方式抽取调度策略的N个解，其中N的值必须非常大(例如1 000个)，并根据用户要求给出最终要得到的足够好的解的个数k、基准概率α。

(2)对这N个解分别做n次试验(n≪N)，例如对N个解做10次实验，获得n次实验的完成时间(J1(θ))和货币成本(J2(θ))的平均值作为其真实性能。

(3)建立二维坐标系，以完成时间J1(θ)为x轴，货币成本J2(θ)为y轴。根据分层算法获得策略的布局情况，可计算出层数(m)以及相应的向量性能曲线图(VOPC)，判断出是属于平坦型、中间型还是陡峭型，并根据式(2)、式(3)调整k和g的值。

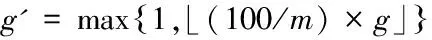
(2)

(3)

(4)根据VOPC的类型，噪声级别，对应线性回归函数表得出Z0、ρ、β、η相应的值，并根据公式s'(k',g')=eZ0(k')ρ(g')β+η计算出被选中的解的集合。该集合相对于实验初选取的N个解的范围至少减少了一个数量级，那么在此基础上能够找到一个或一组相对更好的解，提高了任务调度的性能。最终根据s=「(m/100)×s'⎤对结果进行调整。

以上公式均参考文献[10]。

3 问题解决

3.1 DAG模型

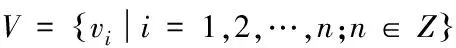
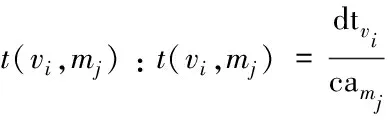
3.2 价格模型

基于Google的定价模型，假设出一种细粒度的定价模型。通常，云提供者针对不同的工作流提供不同类型的虚拟机，而每种类型的虚拟机都存在不同的处理能力和价格模型。文中主要使用两种定价模型，分别是线性定价模型和指数定价模型。其中，线性定价模型中虚拟机的货币成本与CPU周期线性相关，则任务vi在虚拟机mj上执行的货币成本可表示为：

(4)

其中，σ是一个随机变量，用于表示虚拟机价格和处理能力之间的关系，即虚拟机的处理能力越高，则货币成本就越高；camslow表示处理速度最慢的虚拟机mslow所占用的CPU周期；Vcbase则用于标记虚拟机mslow的基价。

在指数定价模型中，虚拟机的货币成本与CPU周期呈指数关系，则任务vi在虚拟机mj上执行的货币成本可表示为：

(5)

那么，任务调度完成需要的总货币成本可表示为：

(6)

在该模型中，忽略了内存空间、网络带宽等因素，这可以作为以后研究的方向。

3.3 调度算法

文中主要考虑两个目标函数，即总货币成本和总完成时间。目标是希望找出一种任务调度方法，使得任务调度最终的总货币成本和总完成时间可以达到最小。然而，货币成本和完成时间本身就是两个相互冲突的目标。因此，基于文献[7]，选取相应数量的任务调度结果集，并基于此采用向量序优化的方法缩小任务调度集，获得一个相对最优解。

具体的算法过程如下:

算法：基于VOO的双目标算法。

Input：一个DAG图，G=(V,E)；

Output：策略集PolicyList。

Procedure：计算每一个任务vi优先级，并降序排列

Foreachvi∈Vdo

Foreachmj∈Mdo

计算目标函数α×T(i,j)+(1-α)×C(i,j)

End

End

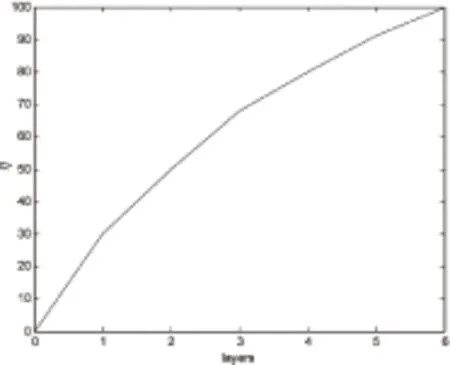
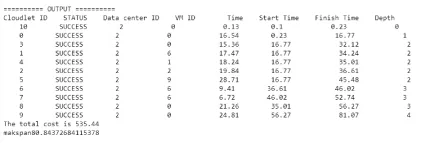
Whilei

Foreachvido

将vi分配给目标函数最小的VM

End

Endwhile

采用序优化方法将所有的解重新布局

计算出VOPC，并得到Z0、ρ、β、η对应的值

计算出最优解集，并从中获得相对最优解

基于以上算法，可以获得一个相对最优解，避免在使用该调度算法时陷入局部最优问题，对于任务调度的完成时间和货币成本都有很大的影响，大大提高了任务调度的效率。此外，在实验中会进一步验证该算法的性能优劣。

4 实验仿真

基于WorkflowSim，实现云计算任务调度仿真实验，并与HEFT进行比较。

4.1 实验环境

实验中所采用的硬件环境是台式机，其具体配置为：Pentium(R)Dual -Core CPUE5500@2.80 GHz，内存为2 GB；软件环境是Windows操作系统、Eclipse集成开发环境，并在Eclipse环境下搭建云平台仿真框架WorkflowSim。为了更加合理地测试实验结果，所运用的数据来源于程序。

WorkflowSim[12]是由南加州大学的Pegasus WMS研究小组开发的工作流仿真软件，是一种基于分布式环境模拟科学工作流的工具包。它在CloudSim[13]仿真软件的基础上，提供了工作流层次的仿真方法，工作流可以以DAG图的形式表示。

4.2 实验结果

以DAG图作为任务调度的输入流，将文中的任务调度算法进行1 000次实验，取其中的100个解，以货币成本(cost)为x轴，完成时间(makespan)为y轴，即任务调度问题的两个性能指标。然后，根据分层算法将这100个解重新布局，得到相应的VOPC，如图3所示。

图3 向量性能曲线图

显然，该向量性能曲线图属于陡峭型，更利于寻找所需的任务调度策略的最优解。对应回归系数表,可以分别求出Z0、ρ、β、η，对应公式则可以求出相对于之前的解集小很多的一个解集，可以得到s=1，即重新布局后的第一层中有所需要的最优解，从第一层选中一个相对最优解，因此可以得到最优解的调度策略，如图4所示。

最后，将提出的算法所得到的最优解与HEFT[14]算法进行比较，HEFT算法得到的解如图5所示。

通过对比可以发现，文中提出的算法所得到的策略任务调度的完成时间在尽可能小的情况下，在货币成本方面得到了改善，但是结果不是最优的；而使用了VOO方法后，基于策略集进行优化得到的结果会更优，也避免了局部最优的问题。因此，文中提出的方法是有效的。

图4 计算后得到的最优解

图5 HEFT算法得到的解

5 结束语

文中主要研究了云计算中的任务调度问题，从完成时间和货币成本两个方面出发，在如何平衡完成时间和货币成本方面有了一定的进展。实验结果表明，采用序优化方法得到的结果能够在完成时间尽可能小的情况下，使货币成本有所下降，并且可以避免任务调度问题陷入局部最优的情况，对于大大提高任务调度的效率具有重要的意义。

[1]ShenaiS.Surveyonschedulingissuesincloudcomputing[J].ProcediaEngineering,2012,38:2881-2888.

[2] 李建锋,彭 舰.云计算环境下基于改进遗传算法的任务调度算法[J].计算机应用,2011,31(1):184-186.

[3] 华夏渝,郑 骏,胡文心.基于云计算环境的蚁群优化计算资源分配算法[J].华东师范大学学报:自然科学版,2010(1):127-134.

[4]HeXiaoshan,SumXianhe,vonLaseewskiG．QoSguidedminminheuristicforgridtaskscheduling[J]．JournalofComputerScienceandTechnology,2003,18(4):442-451．

[5]TordssonJ，MonteroRS，Moreno-VozmedianoR,etal.Cloudbrokeringmechanismsforoptimizedplacementofvirtualmachinesacrossmultipleproviders[J].FutureGenerationComputerSystems,2012,28(2):358-367.

[6]KongXiangzhen，LinChuang，JiangYixin，etal．Efficientdynamictaskschedulinginvirtualizeddatacenterswithfuzzyprediction[J]．JournalofNetworkandComputerApplications，2011，34(4):1068-1077．

[7]SuS，LiJ，HuangQ,etal.Cost-efficienttaskschedulingforexecutinglargeprogramsinthecloud[J].ParallelComputing,2013,39(4-5)：177-188.

[8] 贾庆山.增强序优化理论研究及应用[D].北京:清华大学,2006.

[9]HoYC,SreenivasRS,VakiliP.OrdinaloptimizationofDEDS[J].DiscreteEventDynamicSystems，1992,2(1):61-88.

[10]ZhangF,CaoJ,LiK,etal.Multi-objectiveschedulingofmanytasksincloudplatforms[J].FutureGenerationComputerSystems,2014,37(7):309-320.

[11]IsardM,BudiuM,YuY,etal.Dryad:distributeddata-parallelprogramsfromsequentialbuildingblocks[J].ACMSIGOPSOperatingSystemsReview,2007,41(3):59-72.

[12]ChenWeiwei,DeelmanE.WorkflowSim:atoolkitforsimulatingscientificworkflowsindistributedenvironments[C]//IEEEinternationalconferenceone-science.Chicago,IL:IEEE,2012:1-8.

[13]KumarR,SahooG.CloudcomputingsimulationusingCloudSim[J]．InternationalJournalofEngineeringTrendsandTechnology，2014，8(2):82-86.

[14]TopcuogluH,HaririS,WuM.Performance-effectiveandlow-complexitytaskschedulingforheterogeneouscomputing[J].IEEETransactionsonParallelandDistributedSystems,2002,13(3):260-274.

A Multi-objective Scheduling Algorithm of Many Tasks in Cloud Platforms Based on Method of VOO

ZHU Li-ling,YANG Zhi-ying

(College of Information Engineering,Shanghai Maritime University, Shanghai 201306,China)

Nowadays,cloud computing,as a new technology and business mode,is constantly rising and developing.Scholars at home and abroad have paid great attention to it.However,the problem of task scheduling in cloud platforms is one of the core issues and it’s the hot spot in the area of research on cloud computing.For the scheduling of many tasks in cloud platforms that makespan and monetary costs as two performance metric,an improved algorithm is proposed based on POSH.The algorithm mainly uses method of VOO to optimize the set of task scheduling solution,then can get a semi-optimal good-enough solution from that.In the experiments,compared with HEFT and POSH,it is concluded the proposed method can reduce the monetary cost of the scheduling under the fluctuation of makespan relatively small,which is effective.

cloud computing;VOO;task scheduling;multi-objective;makespan;cost

2016-03-08

2016-06-22

时间：2017-01-04

国家自然科学基金资助项目(61202021)

朱丽玲(1991-)，女，硕士研究生，研究方向为算法设计与分析；杨智应，教授，博士，CCF会员，研究方向为算法设计与分析、在线算法、计算经济学。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1028.048.html

TP301.6

A

1673-629X(2017)01-0011-05

10.3969/j.issn.1673-629X.2017.01.003