基于ARIMA和小波神经网络组合模型的交通流预测

成 云，成孝刚，谈苗苗，周 凯，李海波

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于ARIMA和小波神经网络组合模型的交通流预测

成 云，成孝刚，谈苗苗，周 凯，李海波

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

针对现阶段城市道路交通流预测精度不高的局限性，提出了一种基于差分自回归滑动平均(ARIMA)和小波神经网络(WNN)组合模型的预测方法来进行交通流预测。利用差分自回归滑动平均模型良好的线性拟合能力和小波神经网络模型强大的非线性关系映射能力，把交通流时间序列的数据结构分解为线性自相关结构和非线性结构两部分。采用差分自回归滑动平均模型预测交通流序列的线性部分，用小波神经网络模型预测其非线性残差部分，最终合成为整个交通流序列的预测结果。计算机仿真结果表明：组合模型的预测精度高于ARIMA模型和WNN模型各自单独使用时的预测精度，组合模型可以提高交通流预测精度，是交通流预测的有效方法。

交通流预测；差分自回归滑动平均模型；小波神经网络；组合模型

0 引 言

准确实时的交通流信息在智能交通系统中起着十分重要的作用，因此交通流预测受到广泛关注[1]。其主要预测方法包括3种：基于线性理论的预测方法、基于知识发现的智能模型预测方法、基于非线性理论的预测方法[2]。其中一些预测方法在交通流预测应用中取得了不错的预测效果，但是单个预测方法并不适用于所有交通状态，同时实际的交通流往往既有线性特征，又有非线性特征，仅采用某一种预测模型，难以很

好地反映出时间序列的线性与非线性双重特征，所以应该依据交通流的实际情况来选取合适的预测模型。为了更好地发挥各种模型的预测优势，在1969年Bates等提出组合预测理论，即把多种预测方法组合起来以获得更好的预测效果。Zhang在预测太阳黑子的问题中也采用了组合模型，其预测效果比单个模型更好[3]。

文中使用差分自回归滑动平均(ARIMA)模型和小波神经网络(WNN)模型相结合的方法来预测交通流，利用两种模型各自的优点来提高交通流的预测精度。

1 交通流预测模型

1.1 ARIMA模型

1.1.1 ARIMA基本理论

ARIMA是由自回归滑动平均模型(ARMA)扩展而来。该模型首先对非平稳时间序列作多次差分使其成为平稳时间序列，d即为差分次数，再对差分后的序列建立参数为p、q的ARMA模型，然后由反变换得到原来的非平稳时间序列[4-5]。参数为p、d、q的ARIMA模型预测方程如下：

yt=θ0+φ1yt-1+φ2yt-2+…+φpyt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q

(1)

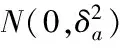
p、d、q是模型的阶数，由不同的p、d、q组合测试可以找到最合适的模型参数[6]。

1.1.2ARIMA算法步骤

ARIMA建模与预测包含四个步骤[7]，如下所示：

(1)序列平稳化处理。

(2)模型识别。一般根据自相关系数与偏自相关系数来确定ARIMA模型的阶数p和q。

(3)参数估计和模型诊断。

(4)用所选取参数的模型来预测时间序列。

1.2 小波神经网络模型

1.2.1 小波神经网络基本理论

WNN是以误差反传神经网络拓扑结构为基础的网络，与BP神经网络类似。在小波神经网络中，信号向前传播的同时，误差反向传播，不同的是小波神经网络隐含层节点的传递函数为小波基函数[8]。WNN拓扑结构如图1所示。

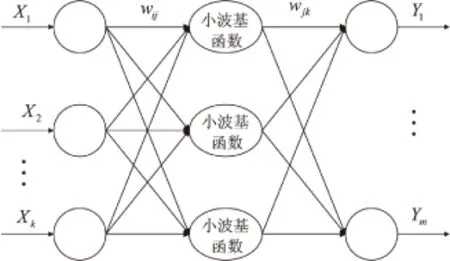
图1 WNN拓扑结构

图1中，X1,X2,…,Xk是WNN的输入参数；Y1,Y2,…,Ym是预测的输出值，即需要求得的最终结果；wij和wjk为网络连接权重值。

当输入交通流量样本序列为xi(i=1,2,…,k)时，隐含层输出为：

(2)

其中，h(j)为隐含层第j个节点的输出；wij为输入层和隐含层的连接权重值；aj为小波基函数hj的伸缩因子；bj为hj的平移因子；hj为小波基函数[9]。

文中的小波基函数是Morlet母小波基函数，公式为：

(3)

小波神经网络输出层计算公式为：

(4)

其中，wik为隐含层到输出层的网络连接权重值；h(i)为第i个隐含层节点的输出；l为隐含层节点个数；m为输出层节点个数[10]。

小波神经网络权值修正是通过梯度修正法来修正网络的权值和小波函数参数，使得网络预测输出不断接近期望输出。步骤如下：

(1)计算网络预测误差。

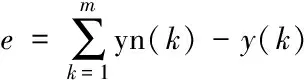
(5)

其中，y(k)为交通流的预测输出结果；yn(k)为交通流的期望输出结果。

(2)通过预测误差e修正相关系数和网络权重值。

(6)

(7)

(8)

(9)

(10)

(11)

其中，η代表学习速率。

1.2.2 小波神经网络算法步骤

WNN训练算法步骤[11]如下：

(1)网络初始化。需要初始化的有伸缩因子、平移因子、网络权重值、学习速率。

(2)样本分类。把样本分为训练样本和测试样本。

(3)预测输出。输入训练样本，获得预测输出，计算预测输出与期望输出的误差。

(4)进行权值修正。通过误差修正网络权值和小波函数参数，使误差控制在一定范围之内。

(5)判断算法是否结束，如果没有，返回步骤(3)。

网络训练完成后，输入测试样本，根据预测输出结果与测试样本输出的对比来评估WNN的性能。综上所述，基于WNN的交通流预测流程如图2所示。

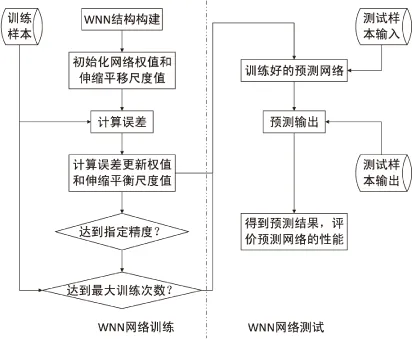
图2 基于WNN的交通流预测流程

1.3 组合模型

实际的时间序列往往既有线性特征，又有非线性特征[12-13]，仅用ARIMA或WNN都不能很好地反映出时间序列的线性与非线性双重特征。因此，它们的组合模型的预测精度可能比其单一模型更高。

把交通流时间序列的数据yt分解为线性Lt和非线性Nt[14-15]，即：

yt=Lt+Nt

(12)

组合模型预测包含三个步骤：

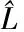
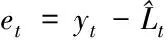
(13)

et=f(et-1,et-2,…,et-n)+εt

(14)

其中，εt表示随机误差。

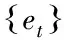
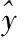
(15)

2 计算机仿真结果

实验中的交通流数据是运用美国加州高速公路通行能力度量系统(Caltrans Performance Measurement System，PeMS)数据库中连续五天的交通数据，数据采样间隔为5 min，数据总数量达到1 440，选择前四天的数据作为样本,对第五天的交通流进行预测。

方法1：单独使用ARIMA模型进行预测。首先对原始交通流数据作平稳化处理，再根据已平稳的时间序列的自相关函数与偏自相关函数图以及AIC最小准则，获得模型参数p，d，q，然后利用该模型进行预测。用Matlab实现仿真。

方法2：单独使用WNN模型进行预测，文中的WNN结构为3-8-1，即输入层3个节点，隐含层8个节点，输出层1个节点，网络反复训练500次。将前三天的数据用于训练网络，第四天的数据用于测试网络。这一过程使用Matlab实现。

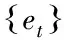
使用平均绝对百分误差(MAPE)来评估算法的预测性能。

图3 3种模型的交通流预测仿真结果

(16)

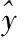
MAPE越小，预测误差越小，模型的预测效果就越好。

用上述3种方法仿真(ARIMA模型、WNN模型、组合模型)获得的交通流预测值和交通流实际测量值的对比见图3。3种算法的平均绝对百分误差对比见表1。

表1 3种方法的平均绝对百分误差对比

由表1可得：组合模型的MAPE最小，表明组合模型的预测效果最好。

3 结束语

在交通流预测中，由于实际的交通流往往既有线性特征，又有非线性特征，仅采用某一种预测模型，难以很好地反映出时间序列的线性与非线性双重特征。因此提出一种ARIMA与WNN的组合模型来预测交通流。用ARIMA模型预测交通流序列的线性部分，用WNN模型预测其非线性残差部分，最后相加得到整个序列的预测结果。通过计算机仿真实验，证明该组合模型比单个预测模型有更好的预测效果。

[1]DaraghmiYA,YiCW,ChiangTC.Negativebinomialadditivemodelsforshort-termtrafficflowforecastinginurbanareas[J].IEEETransactionsonIntelligentTransportationSystems,2014,15(2):784-793.

[2]TeselentisDI,VlahgianniEI,KarlaftisMG.Improvingshort-termtrafficforecasts:tocombinemodelsornottocombine?[J].IETIntelligentTransportSystems,2014,9(2):193-201.

[3]ZhangDC,WangSF.AnovellongtermtrafficforecastalgorithmandcasestudyforChina[C]//Internationalconferenceonadvancedinformationnetworkingandapplicationsworkshops.[s.l.]:[s.n.],2014.

[4]ChanKY,DillonTS,SinghJ,etal.Neural-network-basedmodelsforshort-termtrafficflowforecastingusingahybridexponentialsmoothingandLevenberg-Marquardtalgorithm[J].IEEETransactionsonIntelligentTransportationSystems,2012,13(2):644-654.

[5]WeiW,MaH.ARMAmodelandwavelet-basedARMAmodelapplication[J].AppliedMechanicsandMaterials,2011,121-126:1799-1803.

[6]ErdemE,ShiJ.ARMAbasedapproachesforforecastingthetupleofwindspeedanddirection[J].AppliedEnergy,2011,88(4):1405-1414.

[7]WangL,ZouH,SuJ,etal.AnARIMA-ANNhybridmodelfortimeseriesforecasting[J].SystemsResearchandBehavioralScience,2013,30(3):244-259.

[8]RenCX,WangCB,YinCC,etal.Thepredictionofshort-termtrafficflowbasedonthenichegeneticalgorithmandBPneuralnetwork[M].Berlin:Springer,2012:775-781.

[9]LiuZB,YangZS,GaoP.Researchontheshort-termtrafficflowpredictionmethodbasedonBPneuralnetworks[C]//Worldautomationcongress.[s.l.]:[s.n.],2012.

[10]JiaJ.FinancialtimeseriespredictionbasedonBPneuralnetwork[J].AppliedMechanicsandMaterials,2014,631-632:31-34.

[11] 武志勇,刘东升.小波神经网络在液压装置压力测试中的应用[J].电子测量技术,2010,33(12):91-94.

[12]KhasheiM,BijariM.AnovelhybridizationofartificialneuralnetworksandARIMAmodelsfortimeseriesforecasting[J].AppliedSoftComputing,2011,11(2):2664-2675.

[13] 王 堃,陈涛涛,李 雪,等.基于Matlab的小波神经网络参考作物腾发量预测模型研究[J].沈阳农业大学学报,2013,44(4):457-460.

[14] 赵成柏,毛春梅.基于ARIMA和BP神经网络组合模型的我国碳排放强度预测[J].长江流域资源与环境,2012,21(6):665-671.

[15] 熊志斌.基于ARIMA与神经网络集成的GDP时间序列预测研究[J].数理统计与管理,2011,30(2):306-314.

Traffic Flow Prediction Based on Hybrid Model of ARIMA and WNN

CHENG Yun,CHENG Xiao-gang,TAN Miao-miao,ZHOU Kai,LI Hai-bo

(School of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Aimed at the limitation of low prediction accuracy at the present stage of city road traffic,a prediction method is proposed based on Hybrid Autoregressive Integrated Moving Average (ARIMA) and Wavelet Neural Network (WNN) to predict traffic flow.Using the good linear fitting ability of ARIMA and the strong nonlinear mapping ability of WNN,the traffic flow time series are considered to be composed of a linear autocorrelation structure and a nonlinear structure.ARIMA model is used to predict the linear component of traffic flow time series and the wavelet neural network model is applied to the nonlinear residual component prediction.The simulation results show that the hybrid model can produce more accurate prediction than that of single model,which improves prediction accuracy of traffic flow prediction,and it’s an efficient method.

traffic flow prediction;ARIMA model;wavelet neural network;hybrid model

2016-03-27

2016-06-28

时间：2017-01-04

国家自然科学基金资助项目(61401236)；南京邮电大学引进人才项目(NY214005)

成 云(1994-)，女，研究方向为交通流预测在智能交通系统中的应用；成孝刚，讲师，研究方向为交通流预测在智能交通系统中的应用和雾霾能见度检测。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1039.072.html

U491112

A

1673-629X(2017)01-0169-04

10.3969/j.issn.1673-629X.2017.01.038