基于局部信息融合的正交稀疏保留投影分析

袁安鼎，荆晓远，吴 飞

(1.南京邮电大学 自动化学院，江苏 南京 210023；2.南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于局部信息融合的正交稀疏保留投影分析

袁安鼎1，荆晓远1，吴 飞2

(1.南京邮电大学 自动化学院，江苏 南京 210023；2.南京邮电大学 通信与信息工程学院，江苏 南京 210003)

模式识别领域对于样本分类判别的准则有很多，近期运用比较多的是将原始数据样本的稀疏重构关系保持到投影变换后的样本空间中，从而增加分类的准确性。稀疏保留投影算法(SPP)就是基于该思想发展起来的典型算法。该算法在寻找最佳投影变换时是从样本的全局角度出发，没有考虑到样本总体呈现非线性而局部线性的空间结构，样本间的局部信息对识别率同样有很大的提升作用，同时SPP算法获取的投影变化是非正交的，特征变换之间存在冗余信息，特征信息之间存在冗余的情况对于样本分类过程存在很大的干扰项。基于以上不足之处，提出基于局部信息融合的正交稀疏保留投影，将正交性以及样本间的局部结构信息融入SPP算法之中，同时在AR以及CAS-PEAL人脸库上对所提算法进行验证。

稀疏保留投影；局部近邻信息；正交性；迭代终止准则

0 引 言

在图像特征提取和识别技术中，子空间学习方法使用最为广泛[1-2]，其中最经典的有主成分分析(Principal Component Analysis，PCA)和线性鉴别分析(Linear Discriminant Analysis，LDA)。子空间相关方法能够很好地解决样本“维数灾难”这一难题，该类方法的总体流程是把在高维空间中分布不是太密切的原始图像样本通过非线性或线性投影变换到一个由投影变换矩阵张成的低维子空间中，进而使得变换后的图像样本在子空间中分布较之于变换前更加紧凑，从而简化分类过程中的计算复杂度等一系列问题[3-4]。ULDA[5]是基于LDA算法在投影变换中添加正交约束，使得获取的投影变换具有去冗余信息的特征。

流形学习是一个数学模型概念，在模式分类的应用中代表的是一种空间表示形式，运用流形结构可以轻松准确地解释事物的内在本质结构[6]。对于高维原始图像样本，一般降维算法都是从全局结构对图像样本进行操作，但该做法忽视了图像样本的内在结构，而流形学习算法是从图像样本的局部结构出发，注重的是局部而非全局特性。代表性的算法是LPP，该算法主要通过建立近邻结构图矩阵保留样本的局部结构信息，并在此基础上寻找可以保持样本流形结构的投影变换[7]。

稀疏表示最初是运用在信号处理领域，在过去的信号处理发展中，稀疏表示被成功地应用并解决了很多数字信号领域问题。

在机器学习和模式识别领域，稀疏表示很好地解决了图像分类问题[8]，同时发展出了新的基于稀疏表示的从全局出发的稀疏保留投影算法。

稀疏保留投影(Sparsity Preserving Projections，SPP)参照流形学习思想，核心思想是通过对原始数据样本进行稀疏重构，通过获取的稀疏权重矩阵将样本重构过程中出现的误差控制在最小范围内，以此获取最佳的投影变换矩阵组[9]。

但SPP算法是从样本全局角度出发，并且获取的投影变换是非正交形式的，而样本的局部结构包含更多的鉴别信息，并且投影处于正交形式下可以去除特征中的冗余信息[10]。基于此，文中将稀疏保留投影算法与流形学习和正交投影相融合，提出一种新的人脸特征提取方法，即基于局部信息融合的正交稀疏保留鉴别分析。该算法主要是从样本的局部近邻结构出发，同时考虑投影向量间可能存在有冗余信息的可能性并通过正交性以及局部结构信息保留的做法提高算法的识别率。在AR[11]和CAS-PEAL[12]人脸数据库上的实验结果验证了所提方法的有效性。

1 基于局部信息融合的正交稀疏保留投影分析

1.1 稀疏表示模型

对于给定离散信号b∈iN，以及基本矩阵D，D={d∈iN/i∈I}，可以看出D是由K个基本单位向量组建而成，在对信号进行稀疏表示中，矩阵D是经过原始基信号离散化后重新组建的字典矩阵。对于字典矩阵D中的所有单个列向量，称之为字典原子(Atom)，则字典矩阵的维度大小为K，字典矩阵中字典原子的个数为N。且对于矩阵D，必然有K≥N，那么对于原始给定的离散信号b，通过字典矩阵的替换，则有如下利用字典原子对离散信号的等价表达式：

(1)

其中，x表示对应字典原子的对离散信号稀疏表示过程中所做出贡献的加权稀疏；εT表示该项字典原子逼近后所出现的误差项。

对于字典矩阵D，当张成的空间的字典原子个数与空间的维数相当时，也就是K=N时，在此情况下，字典的维数与原子个数相等[13]，则称此字典为完备字典矩阵(complete)；当K>N时，此时比较原子个数与字典矩阵的维数，由于字典原子个数大于字典的维度，则此时字典是以冗余形式存在的，此字典矩阵称之为过完备稀疏表示字典(over-complete)。对于过完备稀疏表示字典，由于字典中的字典原子是线性相关的，则原始离散的稀疏表示[14]的组合形式肯定远远不止一种。

1.2 稀疏保留投影

SPP算法核心思想是获取原始数据样本间的稀疏重构关系并保持到低维投影空间中，以此增加样本鉴别维度。

(2)

s.t.xi=Xsi

1=eTsi

其中，si=[si1,…,si,i-1,0,si,i+1,…,sin]T是一个n维向量，第i个元素值为零，这表示在向量重构过程中，自身不参与自身的重构流程，sij(j≠i)表示的是xj为了重构xi而所占的比重；e∈Rn是一个元素全为1的向量。

依据上述求解函数计算出每一个xi所对应的权重向量si,i=1,2,…,n，即可获取稀疏权重矩阵s=(sij)n×n。

s=[s1,s2,…,sn]T

(3)

其中，si为式(2)的最优解。

将稀疏表示与SPP的目标函数相对比，根据稀疏表示后所得出的稀疏矩阵，可以看出SPP在对原始图像样本进行稀疏重构时，使用的稀疏构造字典采用的就是原始空间中的所有原始数据集，所以在稀疏重构中，单个数据向量本身是不参与对本身的重构过程的，这也解释了列向量si中第i个向量数据为0的原因。

实际图像样本信息中一般存在角度、光照、遮挡等噪音因素，目标函数中的约束条件一般难以达到，对此问题的解决方式是在允许条件范围下，对最优化问题(2)的约束条件进行如下修改：

(4)

s.t. ‖Xsi-xi‖<ε

1=eTsi

从目标函数(4)中可以看出，约束中对重构误差阈值进行固定设置，并对上述最优化问题进行求解即可获取SPP所需要的稀疏重构矩阵S，其形式如下:

S=sij(n×n)=[s1,s2,…,sN]

(5)

基于获取的稀疏表示系数，通过算法对原始样本空间数据进行降维时，希望能够保留对分类有用的信息，为此定义目标函数：

s.t.wTXXTw=1

(6)

对上式最优化函数进行求解，等同于求解如下问题：

XSβXTw=λXXTw

(7)

其中，Sβ=S+ST-STS。

最终对此目标函数进行求解，并将前d个最大的特征值所对应的特征向量构成系数保留算法最终所需的投影变换矩阵W=[w1,w2,…,wd]。

1.3 目标函数的描述求解

基于SPP算法思想，将近邻结构图矩阵以及正交性约束添加到SPP目标函数中，目标函数如下：

对于原始数据样本X={x1,x2,…,xn}，该样本空间中共有n个图像样本，通过如下最优化问题首先获取样本的稀疏系数si：

min‖si‖1

(8)

1=eTsi

其中，ε为事先设定的误差阈值。

基于样本的类标签信息，可对稀疏重构进行同类样本表示优化，如下形式：

(9)

经过优化后的向量稀疏表示系数即为：

(10)

式(10)表明，经优化的样本稀疏重构只有同类的其他样本进行稀疏表示。则最终的稀疏权重矩阵P∈Rn×n为：

(11)

其中，Pk∈Rnk×nk，k=1,2,…,c。

样本的类标签信息通过如下形式添加到近邻结构中：

(12)

基于以上描述，将样本的类标签信息融入到近邻结构中，同时与稀疏权重矩阵相结合[15-17]。

在此假设vl即为所求解的最优投影变换向量组，定义所提算法目标函数如下：

(13)

s.t.vTXDXTv=1

(14)

目标函数(10)经过推导可转化为如下等价求解形式：

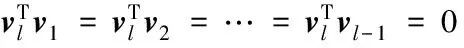
由约束条件中可以看出，约束中添加了正交性以确保对冗余信息的去除。

1.4 投影变换向量求取终止准则

对投影变换向量的求取直接通过目标函数很难得到，在此采取迭代的方式进行，迭代的终止判断条件通过Fisher值进行判断，Fisher值函数表示如下：

(16)

其中，vl表示求解的投影变换向量；J(vl)表示相对应的变换向量的Fisher值；SB和SW分别表示类间散度矩阵和类内散度矩阵，形式如下：

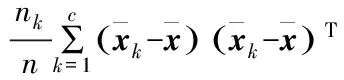
(17)

(18)

迭代终止条件设定如下，特征向量对应的Fisher值大于1时保留，特征向量对应的Fisher值小于1时停止迭代操作。

算法流程总结为：

(1)依据式(9)和式(12)分别计算出原始样本的稀疏权重矩阵P和近邻结构图矩阵w。

(2)通过目标函数(10)经推导化简后求解出等价特征式X(D+PDPT-wPT-PTw)XTv1=λ1XDXTv1，求解第一个投影向量v1。

(3)初始化矩阵V1=[v1]以及M1=[V1]T(XDXT)-1V1。

(4)通过特征等式依次迭代求解投影变换向量，并且更新矩阵Vl=[Vl-1,vl]Vl=[Vl-1,vl]和M1=[V1]T(XDXT)-1V1。

(5)对步骤(4)中求解得到的特征向量通过式(16)进行Fisher值计算，如果J(vl)<1则迭代终止。

2 实 验

对文中所提算法在AR以及CAS-PEAL人脸库上进行验证，将所提算法与LPP、SPP、FSLDA典型算法在识别率效果上进行对比。

2.1 图像数据库介绍

AR库中图像的原始分辨率为768×576，为节约计算成本以及存储空间，选取库中110人，每人有26张图片，并且对图像进行初始化操作，通过降维，每幅图片分辨率大小为60×60。图1显示了AR中一个人的所有图像样本。

CAS-PEAL人脸数据库包含106个人，每人有10幅人脸图像。该数据库的特点是同一个人的不同人脸图像样本受光照影响很大。同样为节约计算成本，实验前将图像处理成60×48大小。图2显示了该库中一个人的所有图像样本。

图1 AR数据库的部分样本图像

图2 CAS-PEAL数据库的样本图像

2.2 实验结果及分析

在AR和CAS-PEAL人脸数据库中对文中所提算法、LPP、SPP、LDA和FSLDA进行实验对比。在AR数据库上，随机选取每类中的12幅图像用作训练集，剩余图像用作测试集；在CAS-PEAL人脸数据库中，每类随机挑选5个样本组成训练样本集，其余组成测试样本集。

图3和图4分别给出了所有方法在AR和CAS-PEAL人脸图像库中随机30次实验的识别效果图。表1给出了其识别率对比数据。

从表1中可以看出，在AR库中，所提算法比LPP的识别率高12.26%，比SPP高7.57%，比LDA高4.70%，比FSLDA高2.82%。在CAS-PEAL库中，所提算法比LPP的识别率高9.92%，比SPP高7.08%，比LDA高7.72%，比FSLDA高6.81%。从实验对比数据可以看出，与相关方法相比,文中所提算法明显提高了识别的准确性。

图3 所有方法在AR人脸库上的识别率

图4 所有方法在CAS-PEAL人脸库上的识别率

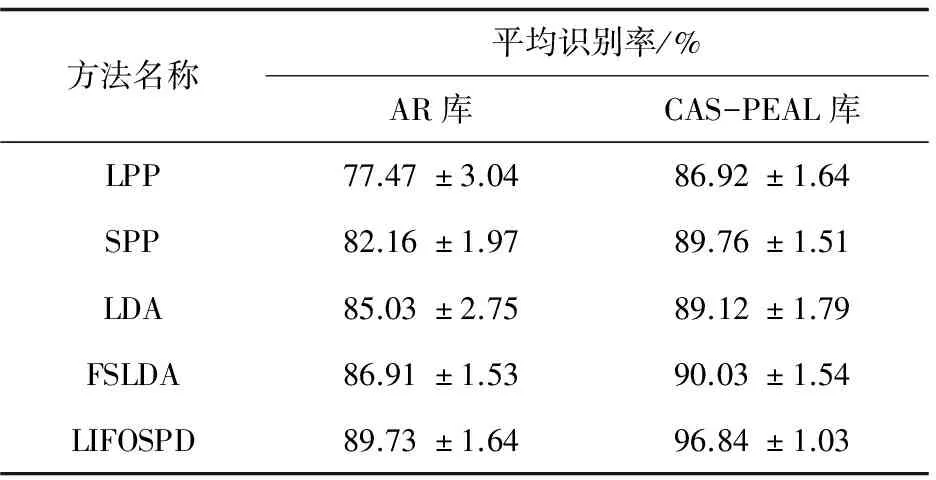
方法名称平均识别率/%AR库CAS-PEAL库LPP77．47±3．0486．92±1．64SPP82．16±1．9789．76±1．51LDA85．03±2．7589．12±1．79FSLDA86．91±1．5390．03±1．54LIFOSPD89．73±1．6496．84±1．03

3 结束语

基于SPP算法的不足，文中将局部结构信息以及正交性引入到SPP算法中，即从样本数据的空间结构出发，同时通过正交性将特征中的相关性去除，通过在人脸库上与相关算法进行对比，验证了所提算法的有效性。

[1] 王李冬.一种新的人脸识别算法[J].计算机技术与发展,2009,19(5):147-149.

[2] 赵振勇,王保华,王 力,等.人脸图像的特征提取[J].计算机技术与发展,2007,17(5):221-224.

[3] Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

[4] Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs. Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[5] Foley D H,Sammon J W.An optimal set of discriminant vectors[J].IEEE Transactions on Computers,1975,24(3):281-289.

[6] Law M H C,Jain A K.Incremental nonlinear dimensionality reduction by manifold learning[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(3):377-391.

[7] Yajing A N. Improved local preserving projection algorithm based on exponential diagonal matrix[J].Computer Engineering & Applications,2011,47(36):197-202.

[8] Hu Zhengping,Liu W,Xu Chengqian.Image inpainting based on non-local sparsity representation with muti-region learning dictionary[J].Mathematics in Practice & Theory,2011,41(7):98-108.

[9] Xiang F,Wang Z,Yuan X.Dissimilarity sparsity-preserving projections in feature extraction for visual recognition[J].Applied Optics,2013,52(20):5022-5029.

[10] Qiao L,Chen S,Tan X.Sparsity preserving projections with applications to face recognition[J].Pattern Recognition,2010,43(1):331-341.

[11] Wang R,Chen X.Manifold discriminant analysis[C]//Proceedings of IEEE conference on computer vision and pattern recognition.Miami,USA:IEEE,2009:429-436.

[12] Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-227.

[13] Sui G R，Cheng L，Chen B X,et al.Research on gait recognition technology based on fiber array sensor[J].Journal of Optoelectronics Laser,2011,22(3):359-362.

[14] Zhang D,Kong W K,You J,et al.Online identification[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(9):1041-1150.

[15] 杨荣根,任明武,杨静宇.基于稀疏表示的人脸识别方法[J].计算机科学,2010,37(9):267-269.

[16] 李 映,张艳宁,许 星.基于信号稀疏表示的形态成分分析:进展和展望[J].电子学报,2009,37(1):146-152.

[17] Donoho D L,Elad M,Temlyakov V N.Stable recovery of sparse overcomplete representations in the presence of noise[J].IEEE Transactions on Information Theory,2006,52(1):6-18.

Analysis of Orthogonal Sparse Preserving Projection Based on Local Information Fusion

YUAN An-ding1,JING Xiao-yuan1,WU Fei2

(1.College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China; 2.College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

There are many sample classification criterion in the field of pattern recognition,and the mostly used one recently is to maintain the sparse reconstruction relationship of original data samples to the sample space after projection transformation so as to increase the accuracy of classification.SPP is a typical algorithm based on the idea.In finding the optimal projection transformation,SPP is based on the global point view,however the spatial structure of the sample is nonlinear and the local linear structure is not considered.At the same time,the SPP algorithm is not orthogonal,and there is redundant information between the feature transform.Based on the above shortcomings,orthogonal sparse preserving projection based on local information fusion is proposed,and the orthogonality and the local structure information of samples are merged into the SPP algorithm.At the same time,the proposed algorithm is validated on the AR and CAS-PEAL face database.

sparsity preserving projections;local neighbor information；orthogonality;iterative stopping criterion

2016-03-25

2016-06-29

时间：2017-01-04

国家自然科学基金资助项目(61272273)；江苏省普通高校研究生科研创新计划(CXLX13_465)

袁安鼎(1991-)，男，研究生，研究方向为生物特征识别；荆晓远，教授，博士生导师，研究方向为模式识别、图像处理、机器学习。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1039.066.html

TP301

A

1673-629X(2017)01-0061-04

10.3969/j.issn.1673-629X.2017.01.014