基于个性化需求的拼车路径匹配算法研究
2017-02-22王丽侠
郭 会,王丽侠
(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学行知学院,浙江 金华 321004)
基于个性化需求的拼车路径匹配算法研究
郭 会1,王丽侠2
(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学行知学院,浙江 金华 321004)
目前,多数城市都存在着打车难、交通拥挤、汽车造成的空气污染严重等问题,而拼车是解决上述问题的有效方法。拼车既可以缓解交通拥挤解决打车难的问题,又可以节能减排,利于环保。面向出租车拼车的个性化需求,提出相应的数学模型,将拼车问题模型化,同时设计一种基于乘客个性化需求的出租车路径匹配算法,规划最优的行车路线,为出租车司机和乘客推荐优化的行车路径和拼车对象。实验结果表明,提出的基于乘客个性化需求的拼车路径匹配算法不仅可以提高搭乘成功率,还明显降低了车辆的运行成本,有利于节能减排,合理利用资源。
出租车拼车;路径匹配;个性化需求;环保
0 引 言
近年来,随着人们生活水平的不断提高,城市化进程日益加快,出租车行业飞速发展[1]。出租车在给人们生活带来便利的同时也存在空车率高、实载率低等现象,由此造成了城市交通拥堵、空气环境污染、交通资源浪费严重等问题[2-4]。“拼车”是提高出租车乘载率,缓解打车困难,解决交通拥堵的有效手段[5]。目前,国内外学者主要研究的是拼车的基本理论,如合乘的发展现状与趋势、组织模式等。对于合乘的许多方面都是定性的分析,丰富了车辆合乘理论[6-9]。虽然部分研究者对合乘做了定量分析[10],但对于合乘路径选择方面的研究,几乎都是针对一对多组织模式建立的数学模型,且考虑的因素与约束比较单一。对于模型的计算,主要采用启发式算法与贪婪式算法来解决车辆的行驶路径问题[11]。
文中提出了一种基于乘客个性化需求的出租车拼车算法,该算法有效解决了不同乘客的拼车请求,提高了搭乘成功率,降低了车辆运行成本。
1 出租车匹配问题的描述及数学模型的建立
1.1 问题描述
文中研究的是两两乘客间拼车路径匹配的问题,它属于多乘客、带有固定时间窗口的合乘匹配问题。具体来说,就是在某个固定区域里,有多辆出租车在行驶,同时有多名乘客有不同的搭乘需求,乘客的出发点和目的地已经确定,并且在上、下车站点对应一个明确的服务时间窗口,乘客必须在规定的时间窗口之内搭乘[12]。文中假定出租车在某个固定的区域里均匀分布,出租车能在较短的时间内到达乘客上车地点。此时忽略出租车到达乘客起始点的时间,这样有利于简化问题。
1.2 问题形式化建模
为描述问题方便,引入以下符号:
查询请求集Q={q1,q2,…,qn}为所有有搭乘需要的乘客的查询请求。其中乘客的请求包括出发地点si,目的地ei,出发时间starti,能够接受的行驶时间runti,即qi={si,ei,starti,runti}。为描述方便,引入以下符号:
S={s1,s2,…,sn}为所有乘客的出发地点集合。
E={e1,e2,…,en}为所有乘客的目的地地点集合。
Z=S∪E∪Z'
其中,Z'表示除上下车点之外,出租车经过的道路节点的集合;Z为所有位置点的集合。
1.3 约束条件
1.3.1 时间约束
乘客能够拼车必须使得每个乘客在各自发出的请求起始时间前能够上车,故乘客间的起始时间差必须大于乘客间起始位置的最短时间mint,即起点约束:
目前乘客对服务要求越来越高,要求必须在规定的时间内到达目的地,即终点约束:

1.3.2 个性化约束
由于每个乘客对于拼车有不同的要求,有的乘客希望节省费用,因此希望能够找到跟他的路线几乎完全匹配的拼车对象,而有的乘客希望节省时间的同时有人能够跟他分担部分费用。基于该考虑,提出一种满足乘客个性化需求的拼车算法,通过控制参数C来满足不同的用户请求。其中,C为起点间距离与终点间距离的总和与该出租车所经过的所有距离的比值:
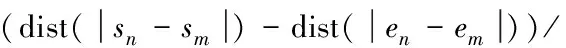
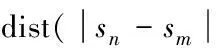
当C=0表示乘客希望找到路径完全匹配的拼车对象,C=0.5表示乘客希望找到至少66.66%路径匹配的拼车对象,C=1表示乘客希望至少50%路径匹配。
1.4 拼车目标
基于乘客个性化匹配问题可将目标分为两个:
(1)满足乘客的个性化需求,且拼车距离最远。
(2)总花费最低。
文中提出一个既有利于司机又有利于乘客的计费方法。
司机的收入为:
CostTax=distmax(n,m)*per*1.2
其中,per为每公里的价格。
出租车拼车过程中,如果司机没有提高收入,将打击出租车司机的积极性,因此设置司机的收入为拼车对象起点终点总费用的1.2倍,由此来激励司机的积极性。
乘客的费用为:
costPassern=CostTax*dist(sn,en)real/ (dist(sn,en)real+dist(sn,en)real)
costPasserm=CostTax*dist(sm,em)real/ (dist(sn,en)real+dist(sm,em)real
其中,dist(sn,en)real表示乘客n从起点到目的地的最短距离。
2 算法设计
由于出租车拼车问题是一个混合整数规划问题,涉及到的约束较多。一般的方法虽然能够求解,但往往结果不够理想[13]。通常对于这样的NP问题,采用贪心算法可以达到较优的效果。对于拼车过程,查询服务质量很重要,因此文中采用贪心算法寻找最优的拼车对象。算法具体描述如下:
输入:查询集合Q={q1,q2,…,qn},qn={sn,en,startn,runtn};用户个性化参数C。
输出:每个能够满足个性化要求的乘客推荐满足条件的拼车对象。
1.对于区域内的所有位置采用SPFA求出所有位置间的最短距离
2.Fori=1ton//对于任何一个查询首先找到满足时间约束的拼车对象
3.For(j=i+1;j 4.If(stC>0){ 5.计算etC1,etC2 6.If(etC1<0&&etC2<0 ){ 7.计算c//c为实际计算出来的参数 8.If(c≤C) 9.putqi,qiintoresultRi} 10.Elsecontinue} 11.ReturnRi//对于每个用户按费用高低给出相应的拼车对象} 12.ReturnR 通过分析上述算法,SPFA的算法复杂度为O(ke)(k<2)。寻找匹配路径时,循环的复杂度为O(n2),所以该拼车算法的复杂度为O(ke+n2)。 为验证算法的有效性及性能,以中国南京市实际路网的某个区域作为研究对象进行实验,该区总共位置为10 000,每条不同的道路有不同的速度即行驶时间的限制。设查询时间为下午5点到晚上9点为验证参数,对参数C的设置进行了对比分析。 实验内容包括:不同参数设置对拼车成功率的影响;不同参数设置对查询时间的影响;不同参数设置对乘客拼车平均时间的影响。 实验环境:Intel@Celeron@CPUE3300,2.50GHz,4GB内存,操作系统为Window7Professional。 首先考虑查询数量对各个指标的影响。此时C=0,查询为随机生成的,时间段设置为交通拥堵的下班高峰期下午5点到晚上9点,因为该时间段对出租车的需求较高。很显然某个时间段查询越多,拼车成功率越高,司机增加的收入越高,用户的付费越低,这是因为拼车的人越多,越能找到匹配度高的拼车对象。实验结果如图1~3所示:相同时间段内拼车查询越多拼车成功率越高,查询运行时间越长,但总体的时间效率是很高的。 然后考虑C值对各个指标的影响。此时查询数量为5 000,C值越大,说明乘客对路径匹配要求越高。当C值为100%时说明乘客希望找到100%路径匹配的拼车对象,很显然C值越小,拼车成功率越低,司机收入越低,用户的付费越少。这是因为C值越大,越难找到匹配度高的拼车对象。一旦找到,乘客间的路径匹配度较高,故司机运行的总路程会减少,故收入会降低。实验结果如图4~6所示。 图1 拼车成功率(1) 图2 拼车查询运行时间(1) 图3 拼车合乘平均时间(1) 图4 拼车成功率(2) 图5 拼车查询运行时间(2) 图6 拼车合乘平均时间(2) 文中构建了个性化出租车拼车路径匹配问题的数学模型,并提出解决此问题的算法。通过对中国南京市的某个时间段,10 000个乘客服务需求的数据结果分析,表明该算法能够在较快时间给出优秀的拼车方案,整体搭乘成本及搭乘成功率较高。还进行了个性化服务需求的实验,结果表明该算法能够满足用户的个性化需求。文中研究的是两两乘客拼车路径匹配问题,尚未涉及更多乘客,也没有出租车的实际分布状况对拼车路径匹配的影响,这也是后期将要开展的研究方向。 [1] 王丽珍.大城市出租车静态和动态合乘模式的探讨[D].长沙:长沙理工大学,2012. [2] 侯惠勤.公共服务蓝皮书:中国城市基本公共服务力评价[M].北京:社会科学文献出版社,2012. [3] 常超凡,陈团生,刘明君,等.城市出租车拥有量对分担率影响分析[J].交通科技与经济,2007,9(3):75-76. [4] 晋江月.拼车的经济学分析[J].科技信息,2006(11):97. [5] 戴云琪.“拼车”行为的问题研究[J].市场周刊:理论研究,2007(11):94-96. [6] 王 罗.出租车共乘问题研究[D].长沙:长沙理工大学,2008. [7]MorencyC.Theambivalenceofridesharing[J].Transportation,2007,34(2):239-253. [8]ShaheenSA,CohenAP,RobertsJD.CarsharinginNorthAmerica:marketgrowth,currentdevelopments,andfuturepotential[J].TransportationofResearchRecordJournalofTransportationResearchBoard,1986(1):116-124. [9]PrettenthalerFE,SteiningerKW.Fromownershiptoserviceuselifestyle:thepotentialofcarsharing[J].EcologicalEconomics,1999,28(3):443-453. [10] 彭霞花.出租车合乘的关键技术研究[D].长沙:长沙理工大学,2009. [11]BarthM,ToddM.Simulationmodelperformanceanalysisofamultiplestationsharedvehiclesystem[J].TransportationResearchPartCEmergingTechnologies,1999,7(4):237-259. [12] 王永明.交通标志自动分割与识别算法及数学模型研究[D].昆明:云南师范大学,2005. [13] 张 瑾,何瑞春.解决动态出租车“拼车”问题的模拟退火算法[J].兰州交通大学学报,2008,27(3):85-88. Research on Carpool Path Matching Algorithm Based on Personalized Needs GUO Hui1,WANG Li-xia2 (1.College of Mathematics Physics and Information Engineering,Zhejiang Normal University, Jinhua 321004,China; 2.Xingzhi College of Zhejiang Normal University,Jinhua 321004,China) At present,there are some common problems such as taxi difficult to call,traffic congestion,heavy air pollution in many cities and so on.Car-sharing is an effective method to solve these problems.Car-sharing can not only ease traffic congestion and solve the problem of taking a taxi is difficult,but also reduce energy consumption and emissions to be helpful for environmental protection.A corresponding mathematical model is proposed and a taxi path matching algorithm is designed based on the individual needs of passengers.In addition,the best route with minimal cost and price is designed to meet the requirement of passengers as much as possible.Experimental results show that the proposed car-sharing path matching algorithm can improve success rate of car-sharing and reduce the travel cost and it is beneficial to energy conservation and emission reduction,reasonable use of resources. car-sharing;path matching;individual needs;environmental protection 2015-05-15 2015-08-19 时间:2017-01-04 国家自然科学基金资助项目(61170108,61402418);教育部人文社科研究项目(12YJCZH142);浙江省自然科学基金(LQ13F020007,LY15F020013) 郭 会(1990-),女,硕士研究生,研究方向为信息安全和隐私保护;王丽侠,副教授,研究方向为智能计算。 http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1017.006.html TP301.6 A 1673-629X(2017)01-0057-04 10.3969/j.issn.1673-629X.2017.01.0133 实验及结果分析
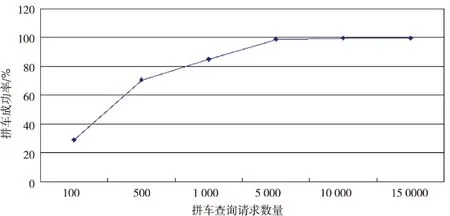


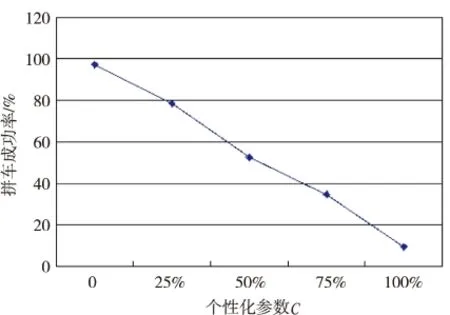
4 结束语
