动态分配聚类中心的改进K均值聚类算法
2017-02-22程艳云
程艳云,周 鹏
(南京邮电大学 自动化学院,江苏 南京 210023)
动态分配聚类中心的改进K均值聚类算法
程艳云,周 鹏
(南京邮电大学 自动化学院,江苏 南京 210023)
K均值算法(KMEANS)是一种应用广泛的经典聚类算法,但其有两个缺陷,即对初始聚类中心敏感及需要人工确定聚类的个数,因而聚类结果的准确率较低。针对K均值聚类算法现存的两个缺陷,为提高算法的精确性与稳定性,以及改善聚类性能,提出了一种改进的K均值算法。该算法通过定义的平均类间最大相似度指标值来确定最佳的K值,将所有数据点中密度较高的点作为备选聚类中心,将备选点中密度最大的两个点作为聚类中心进行初步聚类计算并更新当前聚类中心。当计算得到的平均类间最大相似度现值小于前次计算值,则依据相对距离原则从备选点中动态选择下一个聚类中心;否则,将当前的聚类中心作为最佳初始聚类中心进行K均值聚类计算。实验结果表明,改进后的算法不仅能够有效地提高聚类计算的精确性与稳定性,而且还能缩短聚类计算时间,具有一定的技术优势和应用前景。
KMEANS算法;动态聚类中心;相对距离;高密度点
0 引 言
聚类分析是数据挖掘领域的一个重要分支,是一种无监督的学习方式。聚类分析的主要应用领域有机器学习、模式识别、文本挖掘、图像分割及模式分类等[1]。人们根据不同领域的需求研究出了不同的聚类方法。主要分为基于层次的、基于网格的、基于密度的、基于划分的聚类算法[2]。其中,使用最广泛的是基于划分的聚类算法。基于划分的聚类算法大多是基于数据的距离估计,通过计算数据点与聚类中心之间的距离将数据点分配到最近的聚类中心所在的类中[3]。按这个思想,发展出了不同的聚类算法,最受欢迎的是KMEANS算法。KMEANS算法收敛速度快、算法简单、能有效处理大数据集[4]。但它有两个主要的缺点:手动确定聚类个数和初始聚类中心选择的随机性[5]。
针对KMEANS算法主要从两方面进行改进:获得最佳聚类中心和获得最佳聚类个数[6-7]。对于初始聚类中心的改进,文献[8]提出了最大最小距离的算法,选择相互距离最远的K个数据对象作为初始聚类中心。文献[9]提出了基于密度的改进算法,将密度最大的K个点作为初始聚类中心。这些算法从不同程度上解决了初始聚类中心的随机选择性,一定程度上提高了聚类的精确性,但并没有从根本上解决算法极易陷入局部最优解的问题。对于聚类个数的改进,目前的方法大多是人为定义一些指标用于判断是否达到最佳聚类个数。文献[10]提出了一种确定最佳聚类个数的方法,比较K取所有可能值下的聚类结果,获得最佳聚类个数。该方法可以确定最佳的聚类个数,但当K值变化范围很大时,需要花费大量的时间和精力。文献[11]提出了一种基于距离最大化的K值自动生成算法。该方法一定程度上可以确定最佳的聚类个数,但若初始聚类中心选择到那些异常点时,算法的精度将大幅下降。除此之外,还有一些改进方法,如KMEANS算法与遗传算法相结合[12-13]、KMEANS算法与蚁群算法相结合[14]等等。
文中在分析已有改进算法的基础上,提出一种新的改进算法。该算法通过迭代能自动获得最佳的聚类个数,同时动态分配下一个聚类中心以获得当前状态下的最佳聚类中心。对于同一数据集,该算法有确定的聚类中心,所以它的聚类结果较稳定。
1 KMEANS算法
在基于划分式的聚类算法中,类被视为一种具有相似性质的点簇。数据集中的点被划分到不同的簇,是由它们到给定聚类中心的距离决定的。有几种基于划分式的聚类算法,如:KMEANS算法、KMEDOIDS算法、CLARANS算法。最常用的是KMEANS算法,其基本思想是,首先从数据集中随机选择K个数据对象作为初始聚类中心,将余下的数据对象依据它们与这些聚类中心的相似度(距离)分配到相应的类中。然后计算每个类新的聚类中心,不断重复这一过程,直到评价函数收敛。一般采用簇内误差平方和作为评价函数,其定义为:
(1)
其中,K为聚类个数;P为簇i内的数据对象;ci为聚类中心。
聚类中心的更新依照式(2):
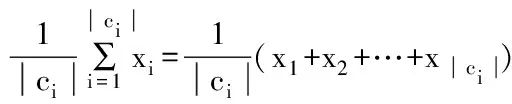
(2)
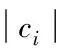
KMEANS算法的执行步骤如下[15]:
输入:包含N个数据对象的数据集,聚类的个数K,算法终止条件(或迭代次数)。
输出:K个簇、评价函数值E、算法运行时间等。
(1)随机选择K个数据对象作为初始聚类中心。
(2)计算余下的数据对象到这K个聚类中心之间的距离(相似度),并将数据对象分配到距离最近的簇中。
(3)根据式(2)重新计算K个簇的聚类中心,并根据式(1)计算相应的评价函数值E。
(4)如果达到最大的迭代次数或相邻两次的评价函数值之差小于ε,则算法停止。否则转步骤(2)。
ε是一个人为定义的数值。当相邻两次的评价函数值之差小于ε时,表明算法收敛。
KMEANS算法具有的优点:简单易实现,运行速率快,能够处理大型数据集。但KMEANS算法也有许多不便之处。例如:初始聚类中心的随机选择导致算法极易陷入局部最优解。同时,算法需要首先确定聚类个数,而这一点是很难做到的。
图1显示相同数据集在不同初始聚类中心下的聚类结果。图2显示相同数据集在不同聚类数目下的聚类结果。图中的数据集是人工数据集。很显然,KMEANS算法的聚类精确度受初始聚类中心和聚类数目的影响很大。

图1 同一数据集不同初始聚类中心下的聚类结果
2 改进的KMEANS算法
在分析已有改进算法的基础上提出一种全新的改进算法。该算法通过比较类间平均最大相似度可以自动确定最佳的聚类个数,还能动态调节当前的聚类中心并动态添加下一个聚类中心。该算法将密度度量和距离度量相结合,从高密度的备选点中选择距离当前更新后的聚类中心相对最远的点作为新的聚类中心添加到当前聚类中心集合中。这样做可以使不同类的聚类中心尽可能相互排斥,从而保证了类间的低相似性。同时,从高密度的备选点中选择下一个聚类中心,这可以保证在同一个类中,聚类中心是一个相对密集区域的点,保证了类内的高相似性。而类间低相似与类内高相似也是对聚类结果好坏的一个评价指标。对于一个数据集,最佳聚类个数一定,使用该算法获得的聚类中心也是固定的,这保证了算法的稳定性。

图2 同一数据集在不同聚类个数下的聚类结果
一些相关的概念及公式定义如下:
点密度:点xi的r邻域内点的个数。
Density(xi)={p∈c|dist(xi,p)≤r}
(3)
其中,xi为类i的聚类中心;r为人为定义的邻域半径。
类内距离:类中每个点到聚类中心之间的距离的均值。

(4)
类间距离:不同类的聚类中心之间的距离。
di,j=‖ci-cj‖
(5)
这里数据对象之间的距离均采用欧氏距离进行度量。
平均类间最大相似度(AMS):每一个类与其他类之间的最大相似度的均值。
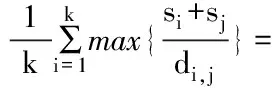
(6)
当AMS取得最小值时,说明聚类效果最佳,此时的K就是最佳的聚类个数。
①冰崩和冰滑坡是引起冰湖溃决的主要诱因。应从遥感、GIS和野外调查三个层面及其组合对冰碛湖进行系统监测。冰碛湖溃决参数包括冰碛湖参数、冰碛坝参数、母冰川参数、冰湖盆参数以及它们之间的相互关系。当前有一些经验方法可以对溃决风险进行定量评估。
改进后算法的执行步骤如下:
输入:包含N个数据对象的数据集,用于判断点密度的邻域半径r,作为备选初始聚类中心的高密度点个数M,初始的AMS值,算法的终止条件。
输出:K个簇、评价函数值E、算法运行时间。
(1)计算每个数据点的点密度,并将点密度最大的M个点加入到备选点集D中。
(2)从集合D中选出密度最大的两个点作为初步聚类中心,并将其从D中删除。
(3)从集合D中选择距离前两个聚类中心最远的点,作为下一个聚类中心,并将其从D中删除。
(4)将N个数据点根据以上聚类中心进行一次迭代划分,并计算AMS值。
(5)如果新获得的AMS值小于上一次的AMS值,算法继续,转步骤(6)。否则,以AMS最小时所对应的聚类中心作为KMEANS算法的初始聚类中心,转步骤(7)。
(7)进行KMEANS聚类。
这里进行最后一步聚类的聚类中心是经过K-1次动态分配而获得的最佳K个聚类中心。它是严格按照数据的特点产生的,而不是随机选择的,因此可以有效避免聚类结果的波动性。同时,由这种机制产生的最佳聚类中心可以很好地避开离群点(那些误差很大的点),因此可以在较大程度上提高聚类的准确性。
3 实 验
3.1 实验描述
为验证文中改进算法的聚类准确性和稳定性,选用UCI数据库上的Iris、Wine、Seeds、Breast共4组数据作为测试数据。由于传统的KMEANS聚类算法和改进的最大最小距离聚类算法对初始聚类中心的选择具有随机性,故对上述两种算法取20次实验结果的均值作为最终的聚类结果。UCI数据库是一个专门用于测试机器学习、数据挖掘算法的数据库。库中的数据都有明确的分类,因此可用UCI数据来检测聚类算法的准确率。表1是用于测试的4组数据的属性。
3.2 实验结果
用随机选择初始聚类中心的KMEANS算法和改进的最大最小距离KMEANS算法以及文中改进算法对以上4组测试数据集进行实验。表2是这4组数据集在不同聚类算法下的聚类准确率。
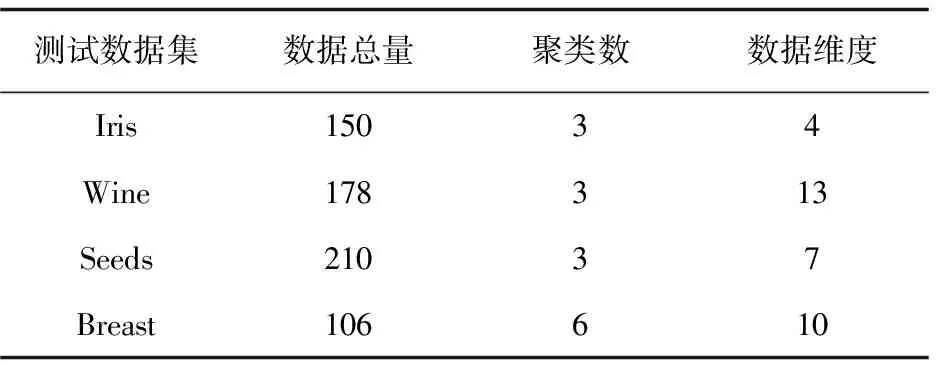
表1 测试数据集属性

表2 传统KMEANS算法与改进算法的准确率 %
由表1及表2可以看出,传统算法在相同聚类数目下,数据维度越大,聚类结果精确率越低。数据总量对聚类结果的精确率也有影响,但影响程度低于数据维度的影响。此外,聚类数目对聚类精确度的影响也很大。文中提出的动态聚类算法相比传统的聚类算法和改进的最大最小距离算法而言,能够不同程度地提高聚类精确度。
表3是4组数据集在这三种聚类算法下的评价函数值(总的误差)。评价函数是用于判断一个聚类效果好坏的重要指标。评价函数值越小,聚类效果越好。

表3 传统KMEANS算法与改进算法的评价函数值
由表3可以看出,最大最小距离算法虽然可以提高聚类算法的精确率,减小误差值,但该算法具有一定的适用范围。在Breast数据集上,最大最小距离算法提高了聚类精确率,但误差值却比传统算法要大。相比于前两种算法,文中算法可以较好地降低误差值。这也一定程度上说明了文中算法具有一定的优势。
图3是4组测试数据集在这三种聚类算法下的聚类时间曲线(单位:s)。
可以看出,最大最小距离算法在Breast数据集上的运行时间要比传统K均值算法长,说明了最大最小距离算法具有一定适用范围。文中提出的动态聚类算法相比以上两种算法,能够很好地缩短运行时间,提高算法效率。

图3 三种聚类算法的聚类时间曲线
3.3 实验分析
综合以上实验结果可知,传统的K均值算法在数据对象增加或数据维度加大的情况下,聚类准确率有所下降。当聚类个数增加时,聚类结果的准确率下降最明显。改进的最大最小距离算法一定程度上提高了算法的聚类精度,但对于某些数据集,它的运行时间以及评价函数值甚至要超过传统的K均值聚类算法。这说明改进的最大最小距离聚类算法只适用于某些特定的数据集。文中提出的改进算法在聚类准确率方面具有很大的提高。同时,与前两种算法相比,很好地降低了聚类时间开销。从评价函数值指标也可以看出这种算法具有一定的优越性。
4 结束语
文中提出的动态分配聚类中心的聚类算法对聚类结果的准确率有很大的提高。相比于传统的K均值聚类算法和改进的最大最小距离算法,由于每种数据集的数据对象一定,经过动态分配的初始聚类中心一定,故该算法的聚类结果较稳定。但这种算法需要计算每个数据对象对于给定邻域内的密度,故随着数据集中数据对象的增大,其时间复杂度也会随之增加。当数据对象十分庞大时,如何降低该算法的时间复杂度,将是下一步需要解决的问题之一。
[1]KanungoT,MountDM,NetanyahuNS,etal.AnefficientK-meansclusteringalgorithm:analysisandimplementation[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2002,24(7):881-892.
[2] 倪志伟,倪丽萍,刘慧婷,等.动态数据挖掘[M].北京:科学出版社,2010.
[3]ChaventM,LechevallierY,BriantO.Monotheticdivisivehierarchicalclusteringmethod[J].ComputationalStatistics&DataAnalysis,2007,52(2):687-701.
[4]SudiptoG,RajeevR,KyuseokS.Cure:anefficientclusteringalgorithmforlargedatabases[J].InformationSystems,1998,26(1):35-58.
[5]XuJinhua,LiuHong.Webusersclusteringanalysisbasedonk-meansalgorithm[C]//IEEE2010internationalconferenceoninformation,networkingandautomation.Kunming,China:IEEE,2010.
[6]LouhichiS,GzaraM,AbdallahHB.Adensitybasedalgorithmfordiscoveringclusterswithvarieddensity[C]//IEEE2014worldcongressoncomputerapplicationandinformationsystems.Hammamet,Tunisia,American:IEEE,2014:1-6.
[7]YedlaM,PathakotaSR,SrinivasaTM.Enhancingk-meansclusteringalgorithmwithimprovedinitialcenter[J].InternationalJournalofComputerScienceandInformationTechnologies,2010,1(2):121-125.
[8] 周 涓,熊忠阳,张玉芳,等.基于最大最小距离法的多中心聚类算法[J].计算机应用,2006,26(6):1425-1427.
[9] 韩凌波,王 强,蒋正锋,等.一种改进的K-means初始聚类中心选取算法[J].计算机工程与应用,2010,46(17):150-152.
[10] 周世兵,徐振源,唐旭清.K-means算法最佳聚类数确定方法[J].计算机应用,2010,30(8):1995-1998.
[11] 刘凤芹.K-means聚类算法改进研究[D].济南:山东师范大学,2013.
[12]GriraN,CrucianuM,BoujemaaN.Activesemisupervisedfuzzyclustering[J].PatternRecognition,2008,41(5):1834-1844.
[13]CristoforD,SimoviciDA.Aninformationtheoreticalapproachtoclusteringcategoricaldatabasesusinggeneticalgorithms[C]//ProcofSIAMICDM.Arlington,American:[s.n.],2002.
[14] 巩敦卫,蒋余庆,张 勇,等.基于微粒群优化聚类数目的K-均值算法[J].控制理论与应用,2009,26(10):1175-1179.
[15]ZhangZhe,ZhangJunxi,XueHuifeng.ImprovedK-Meansclusteringalgorithm[C]//Congressandsignalprocessing.[s.l.]:[s.n.],2008:169-172.
ImprovedK-means Clustering Algorithm for Dynamic Allocation Cluster Center
CHENG Yan-yun,ZHOU Peng
(School of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
KMEANS algorithm is a classical clustering algorithm with popular application.However,there are two defects of it known as sensitivity to initial cluster centers and clustering number needs to determine.Thus,the accuracy of clustering results is rather low.In order to improve its accuracy and stability and ameliorate its clustering performance,an improvedK-meansclusteringalgorithmhasbeenpresentedandacquired.OptimumKvalueisdeterminedfortheimprovedalgorithmbydefiningaveragemaximumsimilarityindexbetweenclasses,andthentwopointswithhighestdensityareselectedasclustercentersforinitialKMEANSclusteringandupdatingthecurrentclustercenteraftertheoneswithhigherdensityhavebeentakenascandidateclusteringcenters.Ifthecurrentvalueofaveragemaximumsimilarityindexbetweenclassesislessthantheformer,thennextclustercenterisdynamicallychosenfromcandidateclustercentersbyprincipleofrelativedistance.Otherwise,thecurrentcenteristakenasoptimumclustercenterforKMEANSclustering.Resultsofexperimentsshowthattheimprovedalgorithmcaneffectivelyboostclusteringaccuracyandstabilityandshortentheclusteringtime.Italsoimpliesbothdefinitetechnicaladvantagesandperspectiveforapplicationoftheimprovedalgorithm.
KMEANS algorithm;dynamic clustering center;relative distance;high density point
2016-04-06
2016-08-17
时间:2017-01-10
江苏省自然科学基金(BK20140877,BK2014803)
程艳云(1979-),女,副教授,硕士生导师,从事自动控制原理、网络优化的教学科研工作;周 鹏(1991-),男,硕士研究生,研究方向为数据挖掘与智能计算。
http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1029.078.html
TP
A
1673-629X(2017)02-0033-04
10.3969/j.issn.1673-629X.2017.02.008
