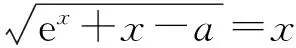破解导数零点难求问题的道与术
2017-02-20汪正文丹阳市教师发展中心江苏丹阳212300
●汪正文 (丹阳市教师发展中心 江苏丹阳 212300)
破解导数零点难求问题的道与术
●汪正文 (丹阳市教师发展中心 江苏丹阳 212300)
导数作为衔接初等数学与高等代数的纽带,是研究函数性质、培养学生探究能力的重要工具,更是历年高考的难点和热点,而导数零点的求解是研究函数性质的前提.文章通过对近几年数学高考导数零点问题的深入探究,给出了导数零点中难求问题的破解之道.
零点;设而不求;等价转化
在近几年的数学高考中,函数与导数备受命题专家的青睐,且多以压轴题的形式出现,主要通过导数研究函数的性质求解,但求导后,导函数形式往往呈现超越式或高次形式,出现导数零点求不出或符号难以判定的情况,从而使问题的求解陷入困境.笔者试图以高考题为例探讨破解导数零点难求问题的道与术.
1 特值验根,证明唯一
导函数存在零点,但令导函数为0后,出现了超越方程,若直接求解比较困难,则可先用特殊值试探出导函数方程的一个根,再通过二次求导研究其单调性,并证明其是唯一的,从而使问题得解.
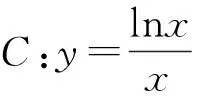
1)求直线l的方程;
2)证明:除切点(1,0)之外,曲线C在直线l的下方.
(2013年北京市数学高考理科试题第18题)
1)直线l的方程为y=x-1,过程略.
因此,除切点之外,曲线C在直线l的下方.
点评 在第2)小题中,令g′(x)=0,得φ(x)=0是超越方程,零点不易求解,但通过观察可知x=1是其零点,再对φ(x)二次求导,知φ′(x)为正,即g(x)为单调函数,说明x=1是g′(x)的唯一零点,从而求出g(x)的最小值.一般地,当导数式含有lnx时,可试根x=1或x=e;当导数式中含有ex时,可试根x=1或x=0.
2 虚设零点,代换化简
导函数零点存在的前提下,当零点式子非常繁琐或无法求解时,可考虑虚设零点x0,然后对f′(x0)=0进行合理地变形与代换,将超越式化为普通式,从而达到化简f(x0)的目的.
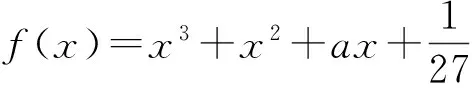
解 三次函数f(x)有3个零点,即f(x)的极大值与极小值异号.由f′(x)=3x2+2x+a,可令f′(x)=0,求得Δ=4(1-3a),接着分类讨论如下:
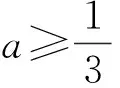
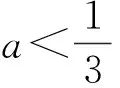
3t2+2t+a=0,
即

于是f(x1)·f(x2)=

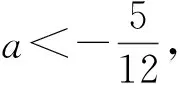
点评 本题零点虽然可求,但若将x1,x2的表达式直接代入f(x1),f(x2),其运算量之大导致求解无法进行.通过虚设零点,利用3t2+2t+a=0进行合理代换与降次,从而达到化简之功效.这种“设而不求”的思想可成功规避零点的繁琐求解.
例3 设函数f(x)=e2x-alnx.
1)讨论f(x)的导函数f′(x)的零点个数;
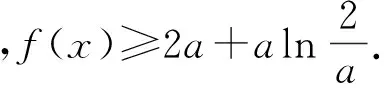
(2015年全国数学高考新课标卷文科第21题)
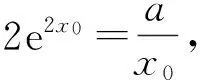
当x∈(0,x0)时,f′(x)<0,从而f(x)单调递减;当x∈(x0,+∞)时,f′(x)>0,从而f(x)单调递增,从而当x=x0时,f(x)min=f(x0).又
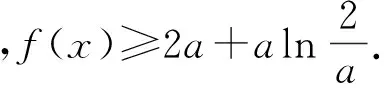
点评 导数含参且存在零点,但无法求出时,可通过虚设零点x0,研究f′(x)的单调性,判断出f(x0)是极大值还是极小值,再利用式子f′(x0)=0进行变形与代换,从而将超越式化为普通式,最后利用基本不等式放缩求解.
3 等价转化,强化命题
当直接构造函数求导较为繁琐、导函数零点无法求出、虚设零点也难以奏效时,可尝试将目标式等价重组.构造2个相对简单且易于求出导数零点的函数g(x)和h(x),通过证明其加强命题g(x)min>h(x)max,从而规避零点,使问题得解.
1)求a,b;
2)证明:f(x)>1.
(2014年全国数学高考课标卷理科试题第21题)
1)a=1,b=2,过程略.
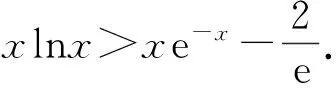
设函数g(x)=xlnx,则
g′(x)=lnx+1,

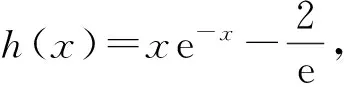
h′(x)=e-x(1-x),
当x∈(0,1)时,h′(x)>0,从而h(x)单调递增;当x∈(1,+∞)时,h′(x)<0,从而h(x)单调递减,故当x=1时,
因此,g(x)min≥h(x)max,又因为当g(x)和h(x)取得最值时,自变量x的取值不同,所以当x>0时,g(x)>h(x),亦即f(x)>1.
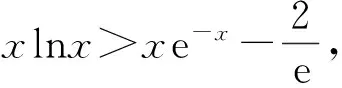
4 分类讨论,分解命题
当整体直接证明较为困难时,可借助某些特殊点将定义域拆分成几个部分,再分情况研究,其中一部分显然成立,另一部分采用放缩的技巧,构造出可求导数零点的函数.
1)求k的值;
2)求f(x)的单调区间;
3)设g(x)=xf′(x),其中f′(x)为f(x)的导函数,证明:对任意x>0,g(x)<1+e-2.
(2012年山东省数学高考文科试题第21题)
1)k=1,过程略.2)略.
3)证明 当x≥1时,
当0
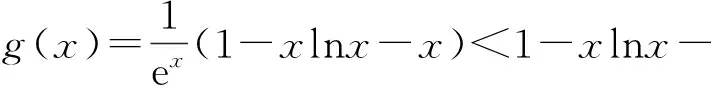
设F(x)=1-xlnx-x,其中x∈(0,1),则
F′(x)=-(lnx+2),
当x∈(0,e-2)时,F′(x)>0,从而F(x)单调递增;当x∈(e-2,1)时,F′(x)<0,从而F(x)单调递减,因此当x=e-2时,
F(x)max=F(e-2)=1+e-2,
故
g(x) 综上所述,对任意x>0,g(x)<1+e-2. 点评 当x≥1时,显然成立,当0 导函数呈超越式,本身没有零点,但可通过研究其二阶导数,乃至三阶导数来判断其正负,从而确定原函数的单调性. (2013年四川省数学高考理科试题第10题) 解 因为y=sinx0∈[-1,1],而f(x)≥0,f(f(y0))=y0,所以y0∈[0,1].又f(x)在定义域内是增函数,若f(y0)>y0,则f(f(y0))>f(y0)>y0与f(f(y0))=y0矛盾.同理,f(y0) a=ex+x-x2. 令g(x)=ex+x-x2,则 g′(x)=ex+1-2x, g"(x)=ex-2, 因此当x∈(0,ln2)时,g″(x)<0,从而g′(x)单调递减;当(ln2,1)时,g″(x)>0,从而g′(x)单调递增,故 g′(x)min=g′(ln2)=3-2ln2>0,即g(x)在[0,1]上单调递增.又g(0)=1,g(1)=e,从而g(x)∈[1,e],于是a的取值范围是1≤a≤e. 点评 导数g′(x)本身没有零点,通过二次求导判断g′(x)符号恒正,从而判定了g(x)的单调性,但之前又无法直观判断零点是否存在,若要一味求解,则只能无功而返.当然本题的另一个难点是如何将问题转化为a=ex+x-x2在[0,1]上有解问题. 导数是研究函数性质的重要工具,而导数零点的求解是研究函数性质的前提.本文所涉及到导数隐零点问题的破解之术也是导数教学的重难点,应熟练掌握并能灵活运用,这样才能更好地发挥导数的功能. [1] 李斌.怎样解决导数零点不可求问题[J].高中数学教与学,2015(5):22-24. 2016-10-13; 2016-11-16作者简介:汪正文(1975-),安徽安庆人,中学高级教师.研究方向:数学教育. O122 A 1003-6407(2017)02-20-035 多次求导,判定正负