汽轮机排汽缸加强筋板的优化设计及影响

陈涛文， 朱燕群， 丁星华

(杭州汽轮机股份有限公司，杭州 310022)

汽轮机排汽缸加强筋板的优化设计及影响

陈涛文， 朱燕群， 丁星华

(杭州汽轮机股份有限公司，杭州 310022)

采用拉丁立方试验设计、三阶响应面近似及Hooke-Jeeves直接搜索算法的组合优化策略对排汽缸下部的加强筋板进行了优化设计，并通过选取大量样本点，研究了加强筋板不同几何参数对排汽缸气动性能的影响，同时在变工况下对筋板优化后的排汽缸进行了校核计算.结果表明：筋板到排汽缸子午平面的距离X和筋板倾角θ对排汽缸气动性能影响较大，而筋板底边到排汽缸出口的距离Y和筋板长度L对排汽缸气动性能影响较小；合理布置筋板，可有效提高排汽缸的静压恢复能力，降低出口不均匀性，但也会增加一定的总压损失.

汽轮机； 排汽缸； 筋板； 优化设计； 数值模拟

汽轮机低压排汽缸是连接末级与凝汽器的重要通道，主要作用是将末级排汽组织引导到凝汽器，并对汽流进行减速扩压，使末级排汽的余速动能转化为压力能.在凝汽器真空度一定的情况下，低压排汽缸良好的扩压性能可有效降低末级出口静压，增加机组的可配置焓降.研究表明[1]，末级余速损失可达45～60 kJ/kg，排汽损失相当可观.

排汽缸结构复杂，气动性能的影响因素众多，国内外学者对不同几何参数对排汽缸气动性能的影响进行了大量研究.陈洪溪等[2]根据多年的试验研究，总结了大型空冷汽轮机低压排汽缸几何尺寸对气动性能的影响规律，给出了排汽缸轴向尺寸、环形扩压管形状尺寸等对排汽缸气动性能的影响，并提出设计扩压器时应遵循“扩散时少转弯，转弯时少扩散”的原则.Finzel等[3]实验研究了扩压器出口高度、上下缸水平结合区面积等对排汽缸气动性能的影响.茅声闿等[4-5]采用正交试验方法设计了影响排汽缸气动性能不同几何因素的正交表格，并采用模型吹风实验对各设计方案进行了比较，分析了各因素的影响并得出各因素的最佳组合.Wang等[6]将改进Kriging模型与最大期望提高准则和小生境微种群遗传算法相结合，开发了一种自适应序列优化(ASKO)算法，对模型排汽缸内、外导流环进行了优化设计.

Kasilov[7]和Zaryankin等[8]分别提出在排汽缸内安装不同形式的长隔板和在排缸下部安装格栅的方法以加强对流动的引导，从而减弱和打碎涡系结构.Kasilov以总压损失为参考对象，通过实验考察了2种不同形式的长隔板，认为这种试图打碎涡系结构的方式并不可取；而Zaryankin等认为加装格栅使大涡破碎成小涡，使通流更加容易，不仅使总损失降低，还大幅降低了机组的振动.谢伟亮等[9]对在排汽缸下部不同位置安装加强筋板后的排汽缸流场进行了数值及实验研究.周兰欣等[10]对排汽缸下部安装加强筋板和蜗壳顶部加装导流部件后的排汽缸进行了数值研究，指出在顶部加装导流部件可在一定程度上减小排汽缸的压力损失.

笔者采用拉丁立方试验设计、三阶响应面近似和Hooke-Jeeves直接搜索算法的组合优化策略对排汽缸下部的加强筋板进行了优化设计，研究了加强筋板不同几何参数对排汽缸气动性能的影响，同时在变工况下对优化结果进行了校核.

1 计算模型及设计参数

计算模型及设计变量如图1所示，为杭州汽轮机股份有限公司某一机型的排汽缸.优化时采用轴向均匀进汽条件，进口边界为质量流量6.665 kg/s，总焓为2 397 kJ/kg，出口边界为面积平均静压20 kPa(将此工况命名为工况1).由于采用轴向均匀进汽条件，排汽缸内的流场关于子午平面对称，故只选取了排汽缸的一半进行研究，同时也可缩短数值计算及优化设计的时间.设计变量X为筋板底边到子午平面的距离，Y为筋板底边到排汽缸出口的距离，L为筋板长度，θ为筋板的倾角.采用排汽缸的进口高度对各参数进行了相对化，即各参数相对值为实际值与排汽缸进口高度的比值，各参数相对值范围见表1.优化的目标变量为总压损失系数pt,loss和静压恢复系数pre，计算公式如式(1)和式(2)所示，优化目标是使总压损失系数最小，静压恢复系数最大.

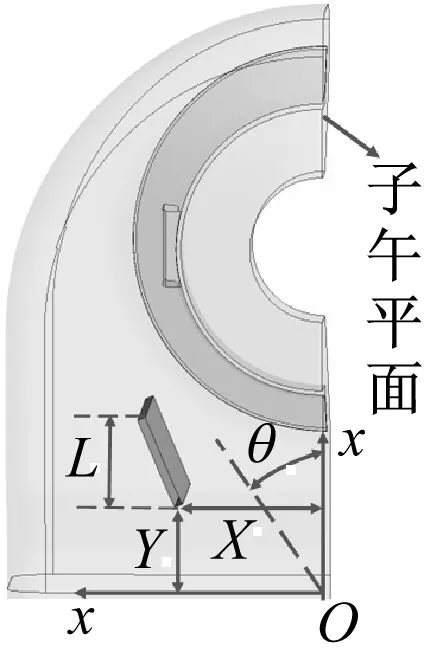
图1 计算模型与设计变量

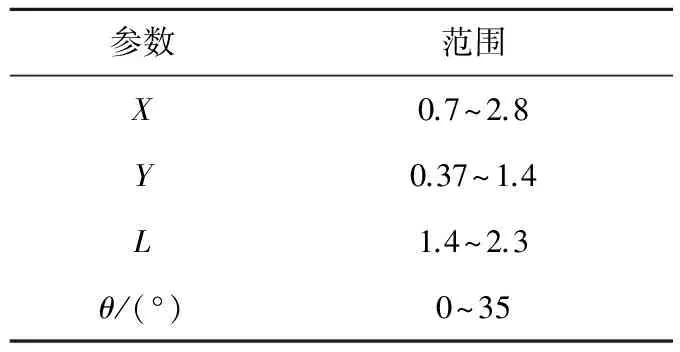
表1 参数范围

(1)

(2)

2 优化流程

优化流程如图2所示，首先，采用拉丁立方试验设计生成设计变量的样本空间，并在Solidworks中完成参数化建模，在CFX14.0中采用标准κ-ε模型完成样本点的计算流体动力学(CFD)计算，并得到相应的总压损失系数和静压恢复系数，生成设计变量-目标变量初始数据库；然后，采用初始数据库中的数据建立初始三阶响应面模型，并用Hooke-Jeeves直接搜索算法搜索出三阶响应面模型(RSM)的最优解；之后，对RSM最优解进行CFD验算，若CFD验算值与三阶响应面模型解在误差范围内，则得到最优解，若二者相差较大，则将CFD验算值加入初始数据库，并重新构造三阶响应面模型，重新搜索，如此循环迭代，直到计算收敛.

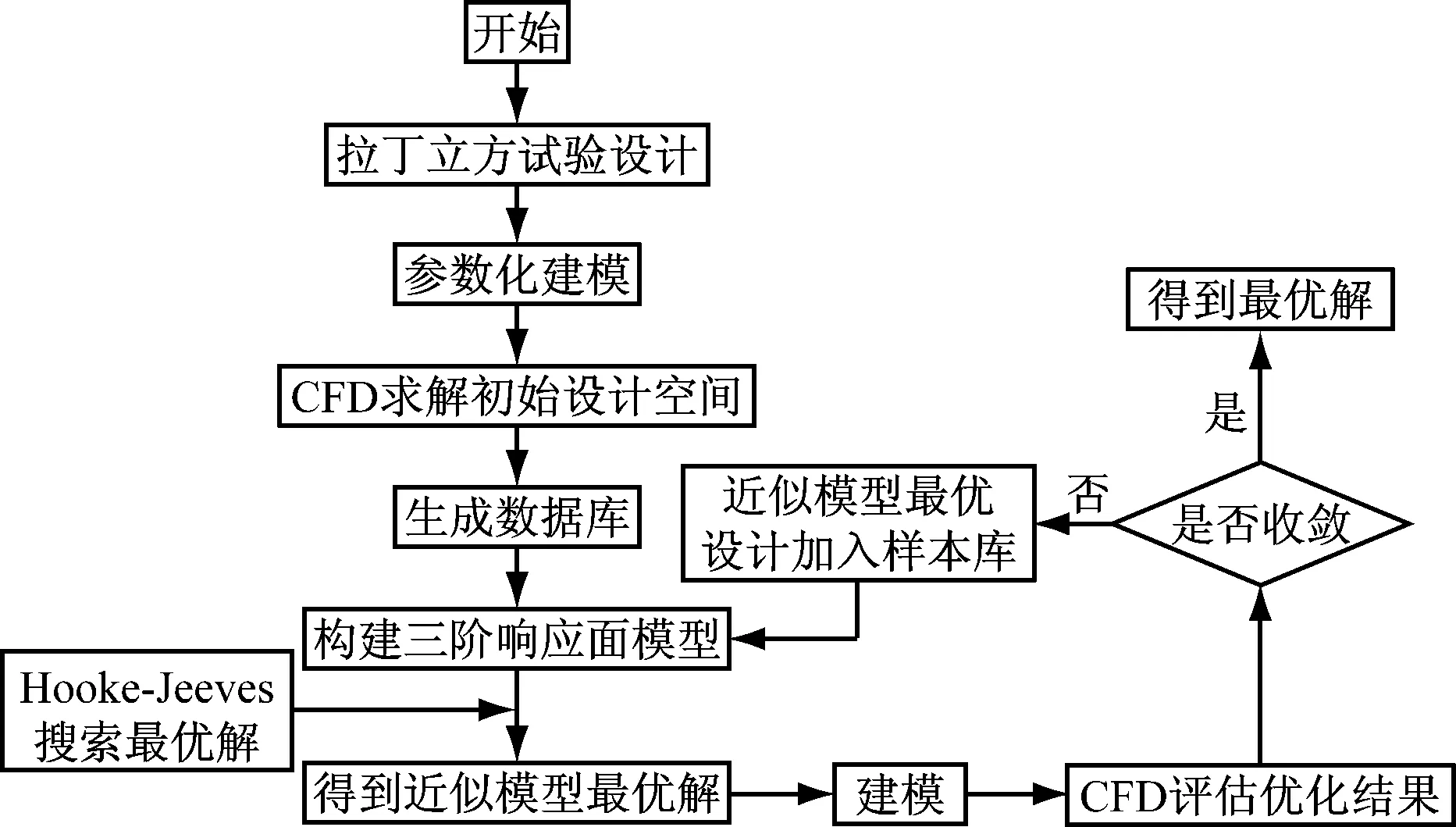
图2 优化流程

3 结果与分析

选用36个样本点构建初始三阶响应面模型，对搜索得到的三阶响应面最优解进行了4次CFD迭代校核.图3给出了校核计算时，总压损失系数和静压恢复系数的收敛曲线，第4次搜索得到的RSM最优解与CFD验算值相差已经很小，可认为计算收敛.

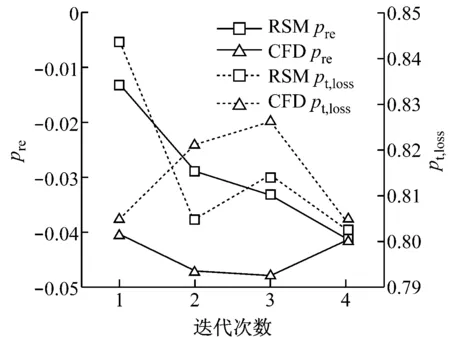
图3 收敛曲线

图4～图7给出了某些参数固定时，根据样本点采用三阶响应面近似拟合出静压恢复系数和总压损失系数随各参数的变化曲线.由图4～图7可知，影响较大的参数是X和θ，而Y与L的影响较小.

图4 静压恢复系数和总压损失系数随X的变化

由图4可知，静压恢复系数和总压损失系数均随着X值的增大而增大，且静压恢复系数与X几乎成线性关系.由图5可知，总压损失系数随着倾角θ的增大而增大，当L较小时，静压恢复系数随θ的增大略有增大然后迅速减小，L较大时，静压恢复系数随θ的增大而迅速减小，因此，θ取0°较合适.由图6可知，随着Y值的增大，静压恢复系数先略微增大，之后快速减小；当Y值变化时，总压损失系数的变动范围很小，L较小时，总压损失系数随Y值的增大逐渐减小，当L较大时，总压损失系数随Y值的变化曲线类似三角函数，但相对变动范围较小.由图7可知，静压恢复系数随L的变化呈类似上凸的二次抛物线，L存在最佳值，最佳L值范围在1.8～2.0内变动，当Y较小时，随着L的增大，总压损失系数先略微减小之后快速增大，当Y较大时，总压损失系数随着L的增大而快速增大.

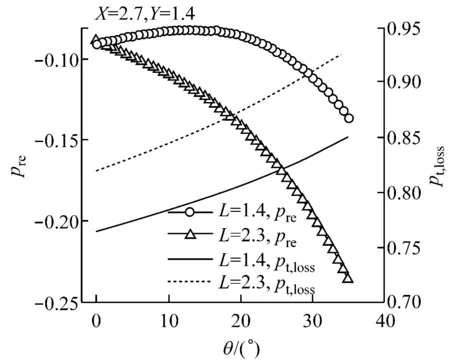
图5 静压恢复系数和总压损失系数随θ的变化

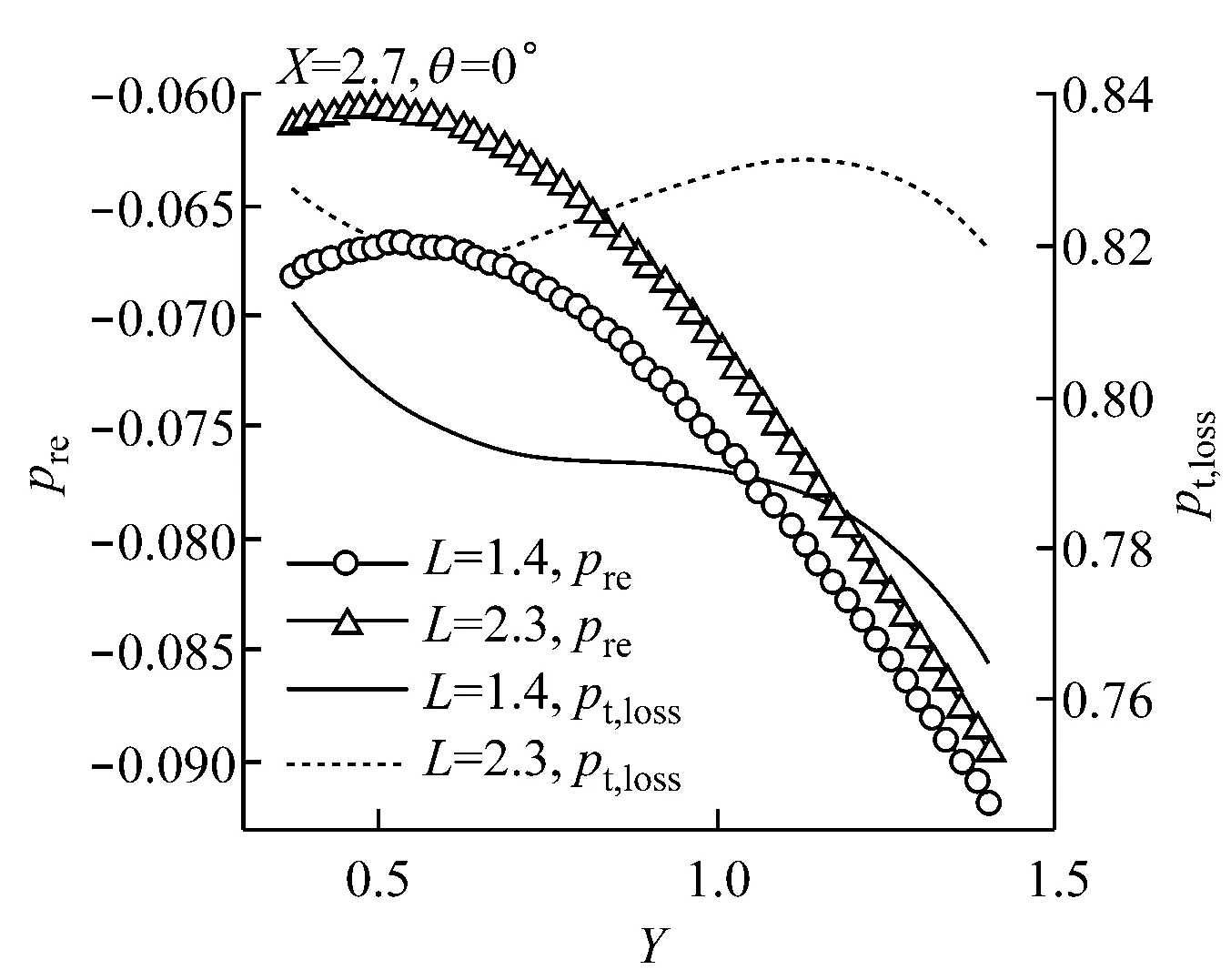
图6 静压恢复系数和总压损失系数随Y的变化

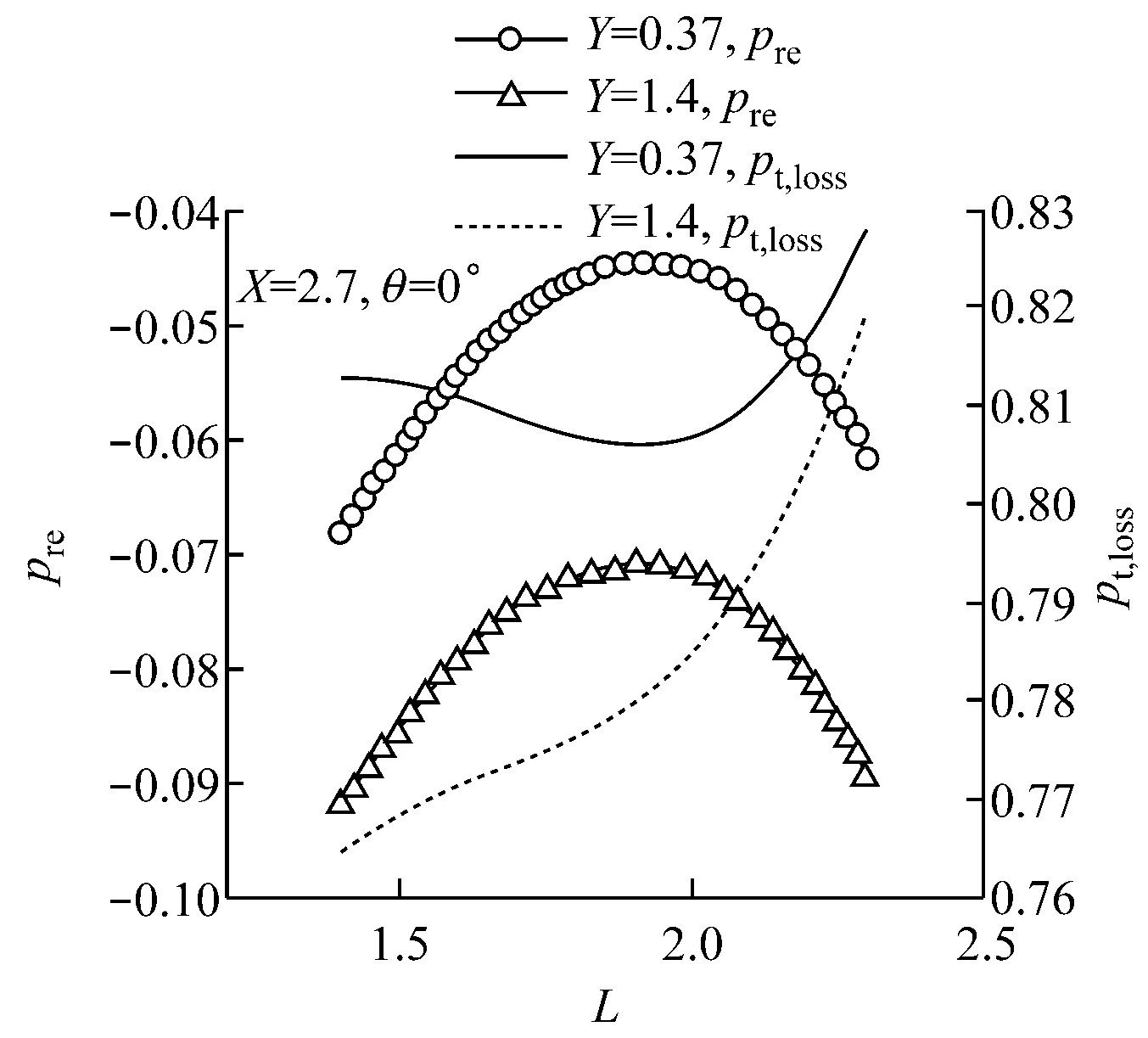
图7 静压恢复系数和总压损失系数随L的变化

表2给出了L=1.45、Y=0.436、θ=0°时，不同X值对应的静压恢复系数、总压损失系数和出口不均匀系数.出口不均匀系数的定义如式(3)所示，其值越小，说明流场分布越均匀.由表2可知，当X=0.7时，与无筋板相比，筋板的存在不仅使得排汽缸的静压恢复能力降低，而且使得总压损失系数增大，随着X值的增大，静压恢复能力逐渐增大，但总压损失也逐渐增大.当X值较大时，排汽缸的静压恢复能力明显高于无筋板时的静压恢复能力.筋板的存在使得出口不均匀系数减小，且X值越大，出口不均匀系数越低.

(3)

式中：h2k为排汽缸出口处的质量流量平均动能；h2kave为进口流量下，假设排汽缸出口截面为均匀流场时的汽流动能.

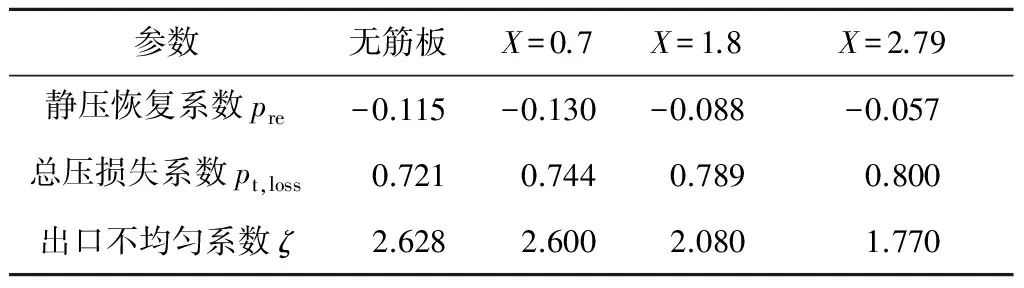
表2 不同X值时的静压恢复系数、总压损失系数及出口不均匀系数

作出无筋板与表2中不同X值时，Plane1、Plane2截面的流线图，截面位置见图8，结果见图9和图10.由图9和图10可知，当X=0.7时，筋板对通道涡基本无打碎作用，且会对边缘的弱旋转汽流产生一定干扰，从而使静压损失和总压损失略微增加；随着X值的增大，筋板越来越靠近通道涡的涡心区域，对通道涡的阻断打碎作用也逐渐增大，当X=2.79时，通道涡已被分割成2个旋转汽流，且由流线的疏密程度可知，旋转汽流的旋流强度也明显减弱.由图10(a)可知，在靠近出口区域，汽流的流线近乎水平，可见其旋转分量很大，旋流强度很大，使得汽流分布很不均匀，排汽缸蜗壳内的空间利用不足.从图10还可以看出，随着X值的增大，筋板对通道涡的打碎作用增大，筋板右侧的回流区也增大，对流场的扰动作用增强，因此，随着X的增大，排汽缸的总压损失增加，同时，由于打碎及扰动作用的增强，使得出口的速度分布更趋均匀.

图8 截面位置示意图

(a)无筋板(b)X=0．7(c)X=1．8(d)X=2．79

图9 不同X值时Plane1截面的流线图

Fig.9 Streamlines on plane 1 for different values ofX

(a)无筋板(b)X=0．7(c)X=1．8(d)X=2．79

图10 不同X值时Plane2截面的流线图

Fig.10 Streamlines on plane 2 for different values ofX

表3给出了X=2.79、Y=0.436时，不同L值时的静压恢复系数、总压损失系数和出口不均匀系数.由表3可知，当L为1.45～2.09时，总压损失系数对L的变化很不敏感，随着L的减小，总压损失系数逐渐减小，但幅度很小，静压恢复系数逐渐减小，而出口不均匀系数逐渐增大，且后两者的变化幅度较大.这是因为当L减小时，筋板对通道涡的打碎作用及对流场的扰动作用减弱，从而使总压损失系数和静压恢复系数减小，而出口不均匀系数增大.

表4给出了X=2.79、θ=0°时，不同L和Y值时的静压恢复系数、总压损失系数和出口不均匀系数.由表4可知，L一定时，当Y值较大时，静压恢复系数较小，总压损失系数有略微减小，出口不均匀系数略有增大；当Y较小时，L越大，静压恢复系数增大，出口不均匀系数减小，总压损失系数略微增大，而当Y较大时，L越大，静压恢复系数减小，总压损失系数略微增大.

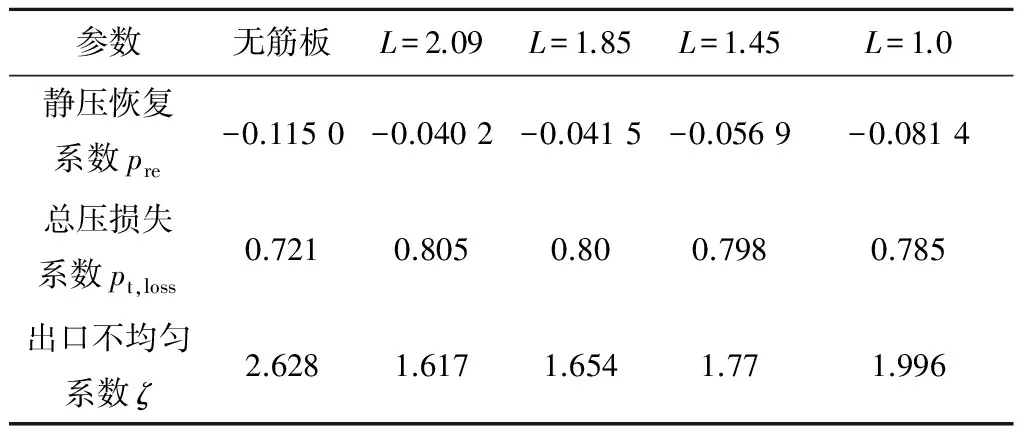
表3 不同L值时的静压恢复系数、总压损失系数和出口不均匀系数

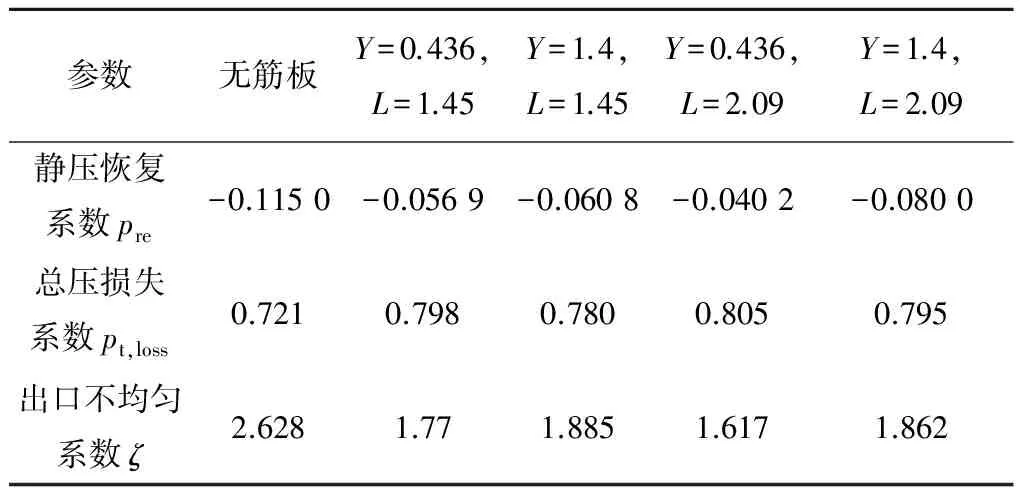
表4 X=2.79、θ=0°时，不同L和Y值时的静压恢复系数、总压损失系数和出口不均匀系数

图11给出了X=2.79、L=2.09、θ=0°时，Y=0.436和1.4时Plane2截面的流线图.由图11可知，当Y值较大时，由于筋板的阻挡，进入外导流环底部蜗壳空间的汽流较少，且由筋板扰动而产生的回流涡更加靠近外导流环，占据了外导流环的底部空间，使得很多汽流集中在筋板左侧的空间内，从而使得外导流环底部空间未被较好地利用，导致静压恢复能力降低；当L值较小时，筋板对汽流的阻挡作用以及对流场的扰动作用均减弱，故当Y值增大时，静压恢复系数减小的幅度降低.由图11还可知，当Y值较大时，筋板左侧流线向下流动更顺畅，使得此时的总压损失系数反而有略微减小.

为了验证变工况下优化后排汽缸的性能，选取了筋板参数为X=2.79、Y=0.436、L=2.09、θ=0°时的排汽缸(暂将此时的筋板参数设置命名为OP1)进行4种工况下的计算，并与相应工况下无筋板时的排汽缸进行了对比.变工况时采用均匀轴向进汽条件，表5给出了4种工况下的进、出口边界条件设置，表6给出了4种工况下排汽缸在无筋板和筋板参数为OP1时的静压恢复系数、总压损失系数及出口不均匀系数.由表6可知，相同工况下，优化后的排汽缸较无筋板时的排汽缸静压恢复能力均有较大的提高；在工况4时，由于进口质量流量很小，2种排汽缸的静压恢复系数均有明显增大，总压损失明显降低，且此种工况下，优化后的筋板对排汽缸的性能提升尤为明显，静压恢复系数由-0.052增大到0.037.

(a)Y=0．436(b)Y=1．4

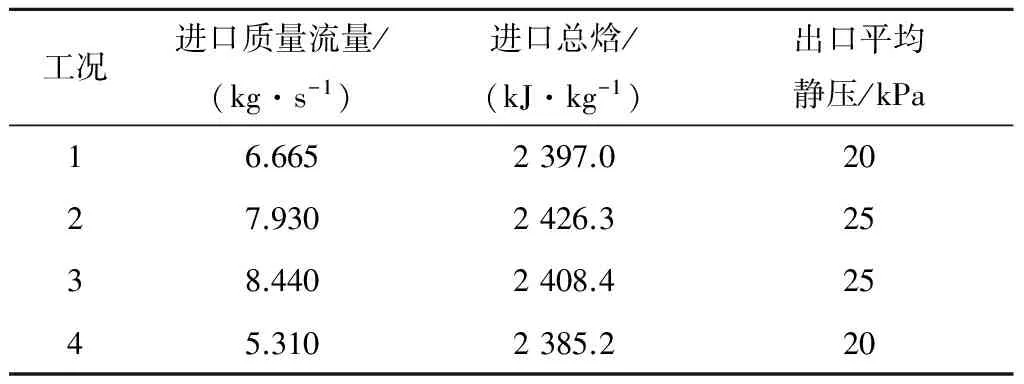
图11 不同Y值时Plane2截面的流线图

表6 4种工况下无筋板及筋板参数为OP1时的静压恢复系数、总压损失系数和出口不均匀系数

4 结 论

(1)与无筋板时相比，合理布置筋板，可有效提高排汽缸的静压恢复能力，降低出口不均匀性，但也会增加一定的总压损失.

(2)筋板底边到排汽缸子午平面的距离X和筋板倾角θ对排汽缸气动性能影响较大，而筋板底边到排汽缸出口的距离Y和筋板长度L对排汽缸气动性能影响较小.

(3)在研究范围内，随着X的增加，筋板对通道涡的阻断打碎作用及对流场的扰动增强，因此，排汽缸的静压恢复能力增强，出口不均匀系数减小，而总压损失增加.随着倾角θ增加，排汽缸的总压损失系数增大，静压恢复系数减小.在一定范围内，当筋板长度L减小时，筋板对通道涡的打碎作用及对流场的扰动减弱，从而静压恢复系数减小，出口不均匀系数增大，总压损失系数略有减小，但总压损失系数降低幅度很小.随着Y的增加，静压恢复系数减小，总压损失系数略有减小，出口不均匀系数增大，且与L较小时相比，L较大时静压恢复系数的降低幅度更大，总压损失系数及出口不均匀系数的增大幅度也更大.

(4)变工况下，优化后的排汽缸性能较原始排汽缸性能均有较大提升，且小流量下提升效果更明显.

[1] ZARYANKIN A E, SIMONOV B P, PARAMONO A N, et al. Advancements in the aerodynamics of exhaust hoods of turbines[J]. Thermal Engineering, 1988, 45(1): 23-27.

[2] 陈洪溪, 薛沐睿. 大型空冷汽轮机低压排汽缸几何尺寸对气动性能的影响[J]. 动力工程, 2003, 23(6): 2740-2743.

CHEN Hongxi, XUE Murui. Effection of geometry dimension on aerodynamic performance of low pressure exhaust hood for large capacity steam turbine with air-cooled condenser[J]. Power Engineering, 2003, 23(6): 2740-2743.

[3] FINZEL C, SCHATZ M, CASEY M V, et al. Experimental investigation of geometrical parameters on the pressure recovery of low pressure steam turbine exhaust hoods[C]//Proceedings of ASME Turbo Expo 2011. Vancouver, Canada: ASME, 2011.

[4] 茅声闿, 魏雨臻, 梅永林. 汽轮机排汽缸气动性能优化的正交试验法[J]. 动力工程, 1987(6): 23-27.

MAO Shengkai, WEI Yuzhen, MEI Yonglin. Orthornormal test of the optimized aerodynamic performance of turbine exhaust hood[J]. Power Engineering, 1987(6): 23-27.

[5] 霍文举. 田口方法优化设计透平排汽缸的应用[J]. 汽轮机技术, 1993, 35(1): 48-55.

HUO Wenju. The aerodynamic optimization of turbine exhaust hood based on taugchi method[J]. Turbine Technology, 1993, 35(1): 48-55.

[6] WANG Hongtao, ZHU Xiaocheng, DU Zhaohui, et al. Aerodynamic optimization system development for low pressure exhaust hood of steam turbine[C]//Proceedings of ASME Turbo Expo 2010. Glasgow, UK: International Gas Turbine Institute, 2010.

[7] KASILOV V F. An investigation of facilities acting on swirl flow in the collection chamber of the exhaust hoods for the low-pressure cylinders in steam turbine[J]. Thermal Engineering, 2000, 47(11): 984-990.

[8] ZARYANKIN A E, GRIBIN V G, PARAMONOV A N. Applying nonconventional solutions to enhance the efficiency and reliability of steam turbines[J]. Thermal Engineering, 2005, 52(4): 267-274.

[9] 谢伟亮, 王红涛, 竺晓程, 等. 汽轮机低压排汽缸内导流挡板对其性能影响的分析[J]. 动力工程学报, 2011, 31(5): 347-351.

XIE Weiliang, WANG Hongtao, ZHU Xiaocheng, et al. Influence of baffle arrangement on performance of related low-pressure exhaust hood of steam turbines[J]. Journal of Chinese Society of Power Engineering, 2011, 31(5): 347-351.

[10] 周兰欣, 陈顺宝, 邵明巍, 等. 汽轮机排汽通道内导流元件对其性能影响的数值研究[J]. 汽轮机技术, 2015, 57(1): 33-36, 60.

ZHOU Lanxin, CHEN Shunbao, SHAO Mingwei, et al. Numerical study on the performance of exhaust steam passage with different guide baffles[J]. Turbine Technology, 2015, 57(1): 33-36, 60.

Optimized Design of a Plate Stiffener for Steam Turbine Exhaust Hood

CHENTaowen,ZHUYanqun,DINGXinghua

(Hangzhou Steam Turbine Co., Ltd., Hangzhou 310022, China)

An optimization was conducted to the design of a plate stiffener located in the lower area of steam turbine exhaust hood using Latin hypercube experiment design, cubic response surface model and Hooke-Jeeves direct search technique. Based on numerical investigation of a large number of samples, the influence of different geometric parameters of the stiffener was studied on the aerodynamic performance of the exhaust hood, which was examined under variable conditions after optimization. Results show that both the distance between the stiffener and the meridian planeXas well as the dip angle of the stiffenerθhave large influence on the aerodynamic performance of the exhaust hood, while the distance between the stiffener bottom and the hood outletYas well as the length of the stiffenerLhave little influence. The static pressure recovery coefficient can be improved effectively by arranging the stiffener appropriately, when the outlet non-uniformity would be reduced; however, this may lead to a certain loss of the total pressure.

steam turbine; exhaust hood; plate stiffener; design optimization; numerical simulation

2016-03-17

2016-05-04

陈涛文(1987-)，男，江西鹰潭人，工程师，硕士，主要从事汽轮机的热力设计及内部流动的数值及实验方面的研究. 电话(Tel．)：13777869784；E-mail：ctwwork@163.com．

1674-7607(2017)02-0105-06

TK262

A 学科分类号：470.30