无磁转台的电子罗盘误差分离标定方法*

高 可， 林新华， 储志伟， 武靖博,3

(1.中国科学院 合肥智能机械研究所 传感技术国家重点实验室，安徽 合肥 230031；2.中国科学技术大学 自动化系，安徽 合肥 230026； 3.合肥工业大学 化工机械研究所， 安徽 合肥 230009)

(1.中国科学院 合肥智能机械研究所 传感技术国家重点实验室，安徽 合肥 230031；2.中国科学技术大学 自动化系，安徽 合肥 230026； 3.合肥工业大学 化工机械研究所， 安徽 合肥 230009)

无磁转台的电子罗盘误差分离标定方法*

高 可1,2， 林新华1， 储志伟1,2， 武靖博1,3

(1.中国科学院 合肥智能机械研究所 传感技术国家重点实验室，安徽 合肥 230031；
2.中国科学技术大学 自动化系，安徽 合肥 230026； 3.合肥工业大学 化工机械研究所， 安徽 合肥 230009)

(1.中国科学院 合肥智能机械研究所 传感技术国家重点实验室，安徽 合肥 230031；2.中国科学技术大学 自动化系，安徽 合肥 230026； 3.合肥工业大学 化工机械研究所， 安徽 合肥 230009)

采用3个分立的磁感式磁传感器和三轴加速度传感器制作了全数字输出电子罗盘；基于自制三轴旋转无磁转台提出了一种电子罗盘标误差分离标定方法。通过无磁转台获取磁传感器敏感轴非正交或未对准的参数和磁传感器输出特性曲线，磁传感器的灵敏度系数因子和偏置量。分别评价偏置、灵敏度系数不一致以及非正交或未对准对电子罗盘方位角精度的影响。实验结果表明：经过校准后，电子罗盘水平面内误差不超过0.22°，而俯仰角和翻滚角在60°内时，方位角最大误差约为0.4°，说明了标定方法的有效性。

电子罗盘； 标定； 误差分离； 无磁转台

0 引 言

电子罗盘通过检测地磁场在水平面内分量方向，以提供方位角信息,被广泛应用于导航领域。电子罗盘一般主要由磁传感器和加速度传感器构成。加速度传感器可测量电子罗盘的倾斜角和翻滚角，从而实现姿态补偿功能[1，2]。此外，磁传感器灵敏度系数、偏置量、磁敏感轴与罗盘外壳轴之间的角度偏差以及外界软硬磁干扰都会扭曲电子罗盘的方位角输出。因此，电子罗盘在使用之必须进行磁传感器标定。目前,针对电子罗盘中的磁传感器，已存在多种标定方法[2～6]。其中，Bowditch P介绍了一种为大家所熟知的“swinging calibration”方法[3]，该方法需要外在的方位角信息作为基准。Honeywell公司的Caruso M J利用水平转台获取磁传感器输出的最大值和最小值，粗略地估计了灵敏度不一致和零点漂移，但没有考虑磁敏感轴非正交对对方位角精度影响[4]。捷克Vcˇ elǎk J报道了一种被称为标量标定的方法，补偿后电子罗盘方位角精度大约为0.6°，但计算量较大，同时不适合现场标定。文献[5]提出了基于椭球拟合算法的误差补偿方法，对电子罗盘的误差来源考虑全面，但需要采集大量的磁传感器的输出数据。

本文设计了一种三轴旋转无磁转台，并相应地提出了一种全新的简易的电子罗盘误差分离方法，可直接确定磁传感器零点漂移或硬磁干扰引起的偏置、灵敏度系数等，达到快速标定校准电子罗盘的目的。

1 三轴旋转无磁转台与电子罗盘硬件设计

三轴旋转无磁转台如图1所示，具有三个互相垂直的旋转轴，垂直度优于0.05°；旋转角度由测量精度为0.001°的光电编码器确定。电子罗盘由三个分离的磁感应(MI)磁传感器和加速度计构成，见图2。

图1 三轴旋转无磁转台

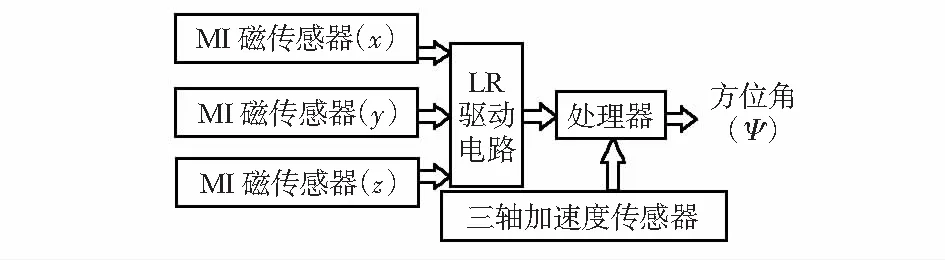
图2 电子罗盘组成框图

2 电子罗盘标定方法

2.1 测量原理

首先，定义几个在电子罗盘标定过程中所需要的几个坐标系，如上图1和图3所示。地磁场坐标系以e表示。其中，xe轴沿着地磁场矢量在水平面内分量的方向，xz轴沿着重力方向，垂直向下，ye轴垂直于xe和ze组成的平面。p为转台坐标系，xp，yp和zp三个坐标轴分别沿着转台三个旋转轴方向，并且zp和ze的方向保持一致。测量坐标系m的三个坐标轴xm,ym和zm分别沿着三个磁传感器的敏感轴方向，并且坐标轴之间彼此不垂直。电子罗盘体坐标系b与电子罗盘长方体外壳保持一致，xb,yb和zb分别沿着长方体外壳相互垂直的三条边。最后一个坐标系l为局域水平坐标系，xl和yl位于局域水平面内,xl与xz的方向一致。上述所有坐标系都服从右手定则。θ和γ分别为体坐标系相对于局域水平坐标系的俯仰角和翻滚角。根据式(1)将体坐标系上磁场强度分量投影到当地水平坐标系上。

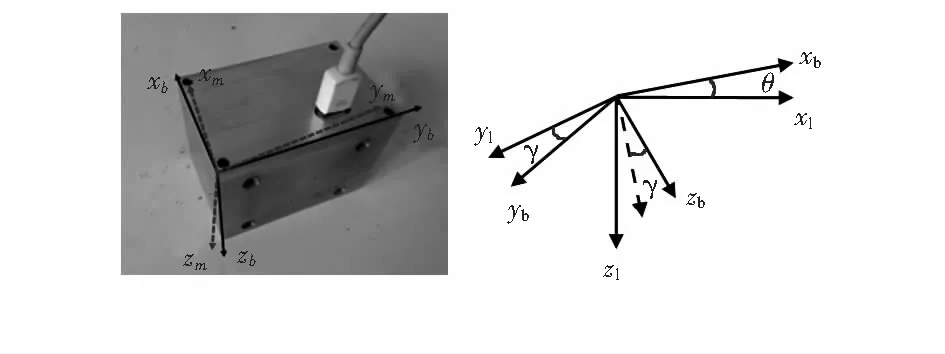
图3 坐标系示意图

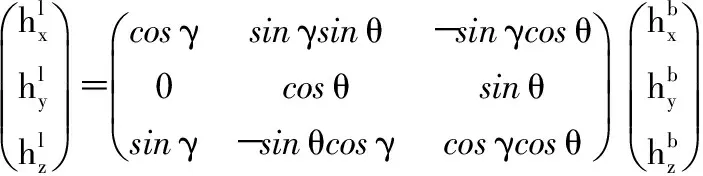
(1)

则方位角(ψ)可由式(2)和式(3)计算得到

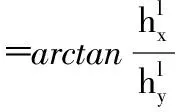
(2)

(3)

2.2 磁传感器误差模型

磁传感器输出信号通常受设备误差和磁场干扰的影响。设备误差包含磁传感器制作或安装过程中引起的零点漂移、灵敏度系数不一致、测量噪音、磁敏感轴彼此之间不正交或磁敏感轴与外壳轴之间没有对准引起的误差。磁场干扰可分为硬磁误差和软磁误差两类。因此，电子罗盘方位角的误差模型为

(4)

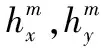
(5)

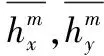
2.3 磁传感器标定

基于上述三轴旋转无磁转台，提出了一种全新的、快速对磁传感器进行校准的误差分离标定方法。首先，将三轴旋转无磁转台的xp-yp平面调节水平；然后将电子罗盘固定于转台xp-yp平面上，并使电子罗盘体坐标系b中xb和zb轴方向与转台坐标系p中xp和zp轴方向保持一致。通过分别旋转转台坐标系中xp,yp和zp轴，寻找磁传感器输出最大值的角度位置，确定测量坐标系m中xm,ym和zm轴与电子罗盘体坐标系b中xb,yb和zb轴彼此之间的夹角∠xmxb,∠xmyb,∠xmzb,∠ymxb,∠ymyb,∠ymzb,∠zmxb,∠zmyb和∠zmzb。同时，还可以得到地磁场矢量与水平面xp-yp之间的夹角φ(磁倾角)以及地磁场矢量在水面内分量与xp轴(转台零刻度线)之间的夹角δ。于是，测量坐标系m与罗盘体坐标系之间的转换关系可由式(6)表示。

[xmymzm]T=[xbybzb]T

(6)

另外，当转台xp-yp平面保持水平时，绕zp轴旋转到一定角度α时，xm方向的地磁场分量可通过式(7)计算得到

sin(α-δ)+cos∠xmzbsinφ]He

(7)

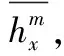
(8)

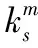
(9)

(10)

由式(5)、式(9)和式(10)，可从测量坐标系敏感轴上的磁传感器输出得到对应体坐标系上的地磁场分量

(11)

3 实验结果

利用自制的三轴旋转无磁转台，采用上述方法进行标定。整个标定过程中室内磁场保持不变。测量坐标系m中xm，ym和zm轴与罗盘体坐标系b中xb，yb和zb轴彼此之间的夹角由表1给出。磁敏感轴与罗盘外壳对应轴的最大偏差角超过2°。图4给出了拟合得到的磁传感器数值输出信号与之检测的磁场分量之间的函数关系，其中He为地球磁场强度。

表1 磁敏感轴与罗盘体坐标系中各轴之间的夹角 (°)

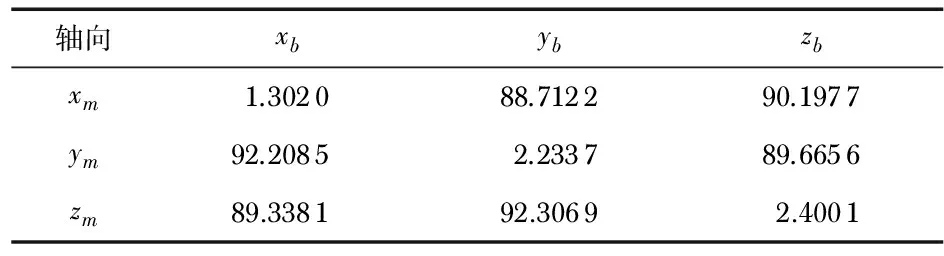
轴向xbybzbxm1．302088．712290．1977ym92．20852．233789．6656zm89．338192．30692．4001

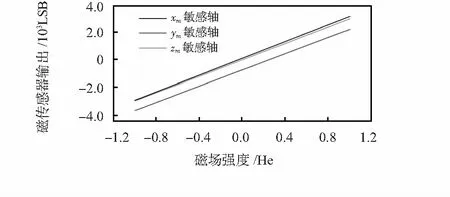
图4 磁传感器数值输出特性曲线

表2 磁敏感轴的灵敏度系数和偏置量 LSB

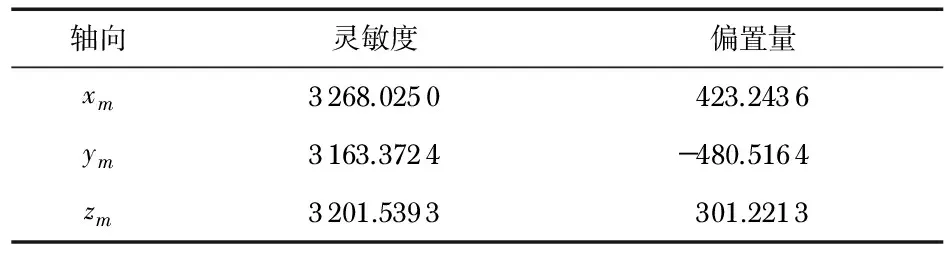
轴向灵敏度偏置量xm3268．0250423．2436ym3163．3724-480．5164zm3201．5393301．2213

至此，根据方程(11)、式(1)、式(2)和式(3)可计算罗盘的方位角。将罗盘固定于转台，并使xl轴与xp方向一致，以转台方位角作为参考值来评估罗盘的方位角误差。图5给出了在转台xp-yp平面保持水平时，绕zp轴旋转任意角度时，计算得到罗盘方位角误差。标定前的罗盘最大方位角误差达20°左右。消除磁传感器偏置引起的误差后，电子罗盘方位角精度改善明显，最大误差降低了约85 %至3°。在此基础上进一步消除磁传感器灵敏度系数不一致引起的误差后，最大方位角误差进一步减小，约为2.4°。再进行非正交校准，电子罗盘方位角精度将进一步提高，最大误差不超过0.22°。

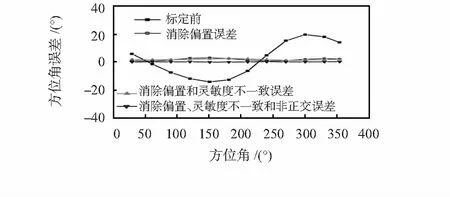
图5 水平状态下电子罗盘方位角误差

另外，根据六位置标定方法[7]，对加速度传感器进行标定，并研究了姿态对电子罗盘方位角误差的影响如图6所示。随着俯仰角θ和翻滚角γ的增加，误差有增大的趋势。但在罗盘的俯仰角和翻滚角同时达到60°情况下，罗盘输出计算的方位角最大误差仅约为0.4°。上述实验结果表明，误差分离标定方法不仅在标定高精度电子罗盘方面十分有效，而且可评估磁传感器的性能；另外，还能分析各干扰因素对电子罗盘精度的影响大小。可以发现，方位角误差绝大部分来源于磁传感器偏置引起的误差。

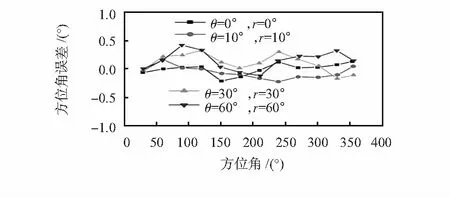
图6 罗盘在不同姿态下的方位角误差

4 结 论

基于自制的三轴旋转无磁转台，提出一种新的电子罗盘误差分离标定方法，并将之用于磁感应式电子罗盘的标定。该误差分离方法不仅能独立地补偿来源于磁传感器偏置、灵敏度系数不一致或敏感轴不互相垂直等引起的误差，并且能对磁传感器的性能进行评价。对于集成的电子罗盘，方位角误差主要来源于零点漂移和磁干扰引起的偏置。但为获得高精度的电子罗盘，灵敏度系数不一致和非正交补偿亦必不可少。在水平状态下，校准后的电子罗盘方位角最大误差约为0.2°。在俯仰角和翻滚角都达60°时，方位角误差也仅为 0.4°左右。校准后电子罗盘具有较高的精度说明基于三轴旋转无磁转台的误差分离方法的有效性。

[2] Vcˇelák J,Ripka P,Kubík J,et al.AMR navigation systems and methods of their calibration[J].Sensors and Actuators A:Physical,2005,123-124:122-128.

[3] Bowditch N.The American practical navigator[M].9th ed.Bethesda:National Imagery and Mapping Agency,1995.

[4] Caruso M J.Applications of magnetoresistive sensors in navigation systems[J].SAE Transactions,1997,106:1092-1098.

[5] Fang Jiancheng,Sun Hongwei,Cao Juanjuan,et al.A novel calibration method of magnetic compass based on ellipsoid fit-ting[J].IEEE Transactions on Instrumentation and Measurement,2011,60(6):2053-2061.

[6] 张爱军,王昌明,赵 辉.三轴电子罗盘的磁方位角误差补偿研究[J].传感器与微系统,2008,27(8):33-35.

[7] Syed Z F,Aggarwal P,Goodall C,et al.A new multi-position calibration method for MEMS inertial navigation systems[J].Mea-surement Science and Technology,2007,18(7):1897-1907.

林新华，通讯作者，E—mail：xhlin@iim.ac.cn。

Calibration method of electronic compass with error-separation based on non-magnetic turntable*

GAO Ke1,2, LIN Xin-hua1, CHU Zhi-wei1,2, WU Jing-bo1,3

(1.State Key Laboratory of Transducer Technology,Institute of Intelligent Machines,Chinese Academy of Sciences,Hefei 230031,China; 2.Department of Automation,University of Science and Technology of China,Hefei 230026,China; 3.Research Institute of Chemical Machinery,Hefei University of Technology,Hefei 230009,China)

Full digital electronic compass is developed by using magnetic-inductive sensors and acceleration sensors and the error-separation method based on non-magnetic three-axis rotation platform is presented to calibrate the magnetic compass.The parameters about misalignment and non-orthogonality of the sensor axes and the response curve of sensor output to earth magnetic intensity are obtained.Furtherly,the sensitivity of magnetometers and the bias from the offset and hard-iron interference are estimated according to the response curve.The independent effect of non-orthogonality and misalignment,bias and inconsistence in sensitivity on the heading error can be evaluated with the error-separation method,respectively.After calibration, the maximum heading error of magnetic compass is about 0.4° when both pitch angle and roll angle are in the range of 60°,indicating the error-separation method is effective and efficient to calibrate electronic compasses.

electronic compass; calibration; error-separation; non-magnetic platform

2016—03—17

国家自然科学基金资助项目(61374016)

10.13873/J.1000—9787(2017)02—0021—04

TP 212

A

1000—9787(2017)02—0021—04

高 可(1990-)，男，硕士研究生，研究方向为检测技术与自动化装置。