水下双斜板结构辐射问题的水动力系数研究
2017-02-17张志强栾茂田王科
张志强, 栾茂田, 王科
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.大连理工大学 工程力学系 工业装备与结构分析国
水下双斜板结构辐射问题的水动力系数研究
张志强1, 栾茂田1, 王科2
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.大连理工大学 工程力学系 工业装备与结构分析国
家重点实验室,辽宁 大连 116024)
本文对一种水下双斜板结构的附加质量和阻尼系数进行了研究。研究中采用的边界元方法可以灵活应用于任意厚度,任意倾角的水下双斜板结构。研究发现:横荡方向附加质量和阻尼系数最大,垂荡方向对倾角变化最为敏感,横荡和横摇方向附加质量和阻尼系数最大值所对应的波浪频率相同。
水下双斜板;边界单元法;附加质量;阻尼系数
近半个世纪以来,关于板式结构的水动力特性问题已经有许多理论和数值研究,发现了很多重要的现象,并取得了众多显著的成果。在目前已知的关于板式结构水动力参数的研究成果中,大部分都是针对平板或立板展开的[1-8],有关斜板的研究并不是很多。然而在海洋工程领域,斜板是一类非常重要且普遍的模型结构,例如斜板式防波堤,船舶减摇鳍,水下航行器的翼型,摇板造波机等都可以简化为斜板结构。因此开展斜板结构水动力参数的相关研究同样非常重要。
关于斜板结构水动力问题的数值研究,最早是由Shaw[9]在1985年展开的。该研究假设薄板以近似接近垂直的角度插入水中,即板倾角非常小,用摄动分析法对该固定不动的微倾斜板的波浪透射系与反射系数数进行了探讨。Mandal等[10]在Shaw研究的基础上,通过格林积分定理进一步给出了透射系数与反射系数的一阶修正量。Mandal等[11]将上述算法扩展到位于自由水面以下的接近垂直的微倾斜板与波浪作用问题中。Parsons等[12]以高阶奇异积分方程为基础,通过切比雪夫多项式逼近薄板两侧的不连续速度势,研究了无限水深情况下部分伸出自由水面的倾斜薄板的透射系数与反射系数。随后,Midya等[13]又将Parsons和 Martin的方法推广到有限水深情况下的水下斜板与波浪相互作用问题中,研究了其透射系数,反射系数以及板上波浪力。
Kharaghani等[14]以一种迎浪端伸出自由水面的浮式斜板为研究对象,将计算区域分为3个子域,利用有限元方法求解其近场速度势,远场速度势采用特征函数展开法进行匹配,研究了其透射系数和反射系数,并通过伯努利方程来计算结构表面动压力,进一步研究了其运动幅值。该研究中只考虑了一种模型:板采用两根弹簧固定,一根弹簧将板的一端与水底相连,板下空隙为水深的30%;另一根弹簧斜拉住该板,使板与水底呈18.43°夹角。Sobhani等[15]针对另一种采用铰接方式固定的迎浪端伸出自由水面的斜板的波浪透射系数进行了数值研究,并通过模型试验对其数值计算结果进行了验证。其数值研究中近场采用有限元方法求解,远场辐射条件采用特征函数展开法来匹配。该研究考虑了两种模型:一种是板的一端直接铰接于水底,通过锚链斜拉使之与水底成18.43°夹角;另一种模型是板的一端铰接于水深的70%处,通过锚链斜拉使之与水底成18.43°夹角。Cho 等[16]将边界元方法与特征函数展开法相结合,研究了直墙前固定不动的倾斜透空板与波浪相互作用的透射系数,反射系数以及波浪力。该方法将计算区域分成内外两个区域,外域用特征函数展开法,内域采用多域边界元方法,并在公共边界匹配连续的速度和压力条件。
在以上关于斜板的研究中,大多数学者研究的都是波浪的透射系数与反射系数,对斜板在流体中做辐射运动的水动力特性问题鲜有涉及。关于斜板的厚度处理问题,文献 [12-13]建立了一个高阶的奇异积分方程,求解的未知量为薄板两侧速度势的差值,从而将薄板处理成无厚度的情况。该方法数学推导复杂,不适用于实际工程问题的研究。其他文献[9-11,14-16]对于板厚的处理没有明确说明。根据数值计算经验,如果采用文献[14-15]中的有限元方法求解近场问题,当板厚非常小的时候,其计算代价将会很高,并且求解远场的特征函数展开法相对更加复杂。
当考虑板的辐射问题时,若板的倾斜角度较大,使用上述解析法或者区域特征函数展开等方法对其进行研究,其公式推导或数值计算将会变得非常困难,一个比较好的方法是采取边界单元法。边界单元法作为海洋工程领域波浪绕射和辐射问题研究中普遍使用的数值方法,其计算精度和可靠性已被广泛验证[17-18]。本研究小组已经成功应用带有波动项的格林函数的边界单元法对位于水面或水下的平板和立板结构的波浪绕射和辐射问题进行了研究[19-20],成功解决了以下两个关键性问题:一是板的任意厚度问题,在板厚为0.005 m的情况下仍然能够得到可靠的计算结果;二是采用直接计算波浪绕射势的方法计算结构所受波浪力,解决了板在波浪作用下的运动响应问题。本文在已有平板和立板的研究基础之上,将上述方法推广到一种倾角较大的,呈“/ ”形布置的水下双斜板式结构,首先研究不同相对板长和倾角对该结构辐射运动时的附加质量和阻尼系数的影响。文章第一节简要介绍了本研究所采用的数学模型和附加质量以及阻尼系数的计算方法,第二节为边界积分方程的离散求解,第三节为算例验证,第四节对附加质量和阻尼系数的计算结果进行了分析。第五节为结论,总结归纳了不同相对板长和倾斜角度对附加质量和阻尼系数的影响规律。
1 基本理论
如图1所示,取笛卡尔坐标系oxy,其中x轴为静水面,y轴垂直向上,S0为物面边界,板的长度方向与y轴正半轴夹角定义为倾角α。两块刚性薄板位于自由水面以下,对称分布于y轴两侧。板的长度均为B=2a=0.4 m,厚度均为TT=0.005 m。两块板的上边缘距离无扰动的自由水面HS=0.05 m, 板的上边缘之间的距离为TS=0.1 m。

图1 计算示意图Fig.1 Calculation sketch
对于图1所示结构的辐射问题,通常假设流体为无粘,无旋且不可压缩的理想流体。在频域内计算势流场时,存在空间复速度势函数φ(x,y)满足如下控制方程和边界条件:
(1)
基于线性假定,复速度势φ可分解为如下形式:
(2)

辐射势φj满足的边界条件为:
定义2(请求者的类型(RC))用户根据自己与消息请求访问者的亲密程度来对请求者进行分类,在社交应用中可以把请求者分成家人、朋友、陌生人等。
(3)
式中:n1,n2,n3为物面法向向量分量,n1=nx,n2=ny,n3=(y-y0)nx-(x-x0)ny,(x0,y0)为物体的旋转中心坐标。
φj可以通过格林定理在物面边界上建立边界积分方程的方法获得。应用格林公式,可以得到下述边界积分方程:
(4)
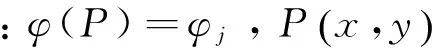
(5)
其中:
(6)
(7)
如果定义:
(8)
式中:ajk为附加质量,bjk为阻尼系数。
2 边界积分方程的离散求解
用边界单元方法将方程(4)在物体积分表面上离散为一系列单元时,假定各物理量在单元间为线性分布,即采用等参单元,则任一单元边界形状和物理变量可表示如下:
(9)
其中,N1(ζ)、N2(ζ)为形函数,可表示为
(10)
式中:(x1,y1)、(x2,y2)为单元j节点整坐标,lN为单元长度,ζ为局部坐标。
将式(9)、(10)代入方程(4),则方程(4)可写成以下形式:
(11)
式中:
(12)
式(12)中含logr1项的系数计算可采用线性解析方法得到,logr2和波动项IC为正则项,其积分不含奇异性可直接用数值方法求得[19]。
3 算例验证
由于现有文献中没有专门针对本文所提出的水下双斜板结构做辐射运动的研究,因此本文通过Midya等[13]关于水下单斜板反射系数的研究成果对本文所采用的方法进行合理性与正确性验证。选取Midya[13]其中一组反射系数结果作为参照,其模型参数如下:d/h=0.1,a/h=0.1,α=45°。其中d为潜深(板中心点距自由水面的距离),h为水深,a为板长的一半,α为板与垂直方向的夹角, 且板的迎浪端高于背浪端。根据文献中各参数之间的比例关系,确定本文验证算例参数如下:半板长a=0.2 m,板厚为0.005 m,浅深d=0.2 m,板上节点总数为200个。如图2所示,本文计算结果与文献Midya[13]中结果吻合较好。

图2 水下单斜板反射系数与文献[13]等人结果对比Fig.2 Reflection coefficient of single submerged inclined plate compared with [13]
4 结果与分析
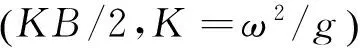
由图3可以看出,在0
由图4,当K=0时,横荡方向的阻尼系数为0,不产生向外传播的波浪。随着相对板长的增加,横荡阻尼系数首先急剧增加,在KB/2=0.5时达到最大值0.09,之后又迅速减小。在KB/2<0.3范围内,不同倾角所对应的阻尼系数曲线基本重合,说明在该范围内改变板的倾角对附加质量影响较小。当KB/2>0.3时,增加板的倾斜角度,会令阻尼系数有所减小,且倾角越大,阻尼系数减小的幅度越大。
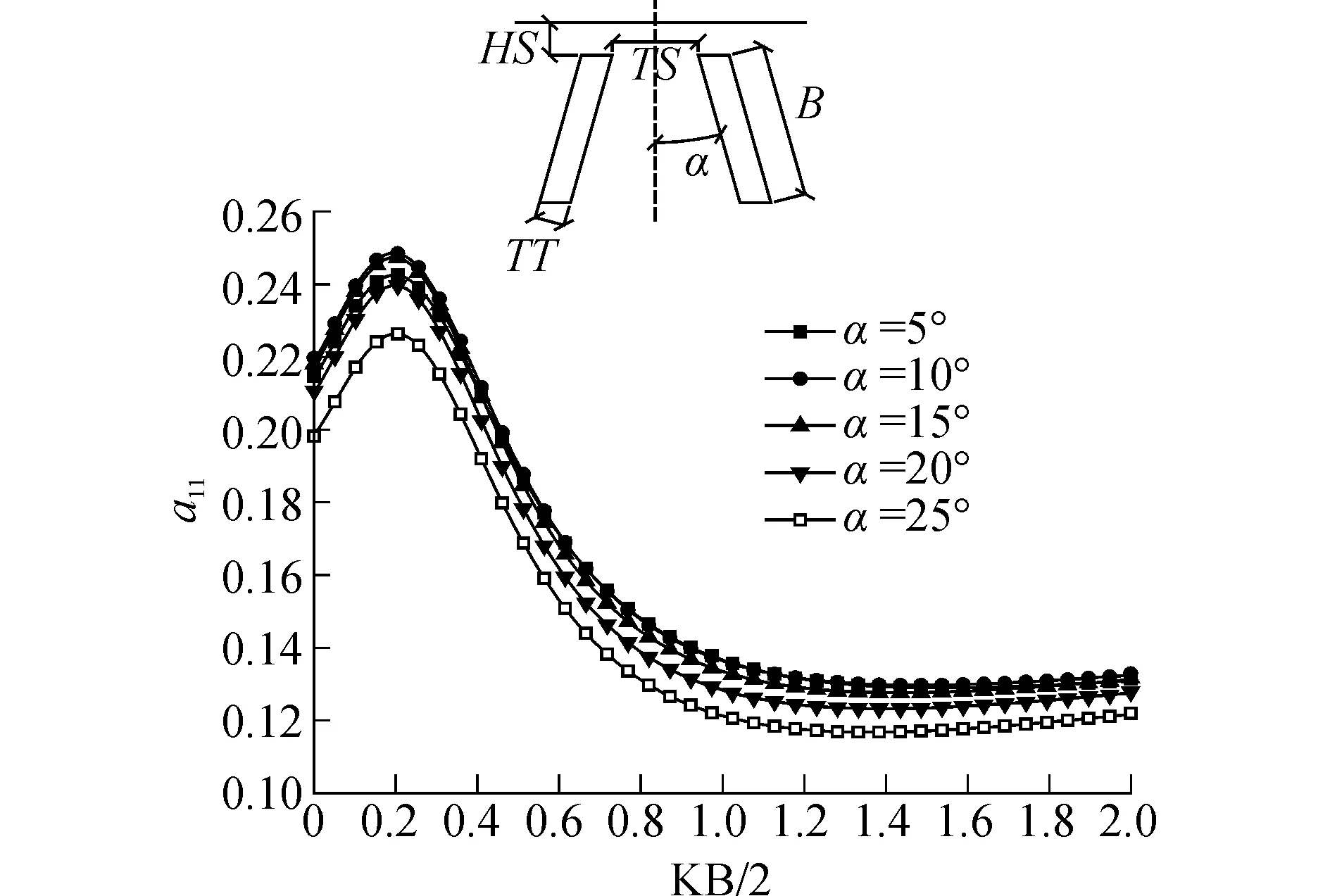
图3 横荡附加质量Fig.3 Added mass for sway

图4 横荡阻尼系数Fig.4 Damping for sway
图5和图6为垂荡方向的附加质量和阻尼系数计算结果。由图可以看出,垂荡方向的附加质量和阻尼系数都很小,这是因为该结构在垂荡方向的投影面积较小。但是垂荡方向附加质量和阻尼系数对倾角的变化最为敏感。在整个频率范围内,增加板的倾斜角度,会令垂荡附加质量的量值有大幅度增加,并且倾斜角度越大,附加质量增加幅度越大。同时,倾斜角度的增大还会令附加质量结果曲线波动幅度变大。由图5可以明显看出,当板的倾斜角度α=5°时,附加质量曲线近似为一条直线,且值都接近于0。当板倾斜角度为α=25°时,垂荡附加质量最大值约为0.06,且在整个频率范围内出现了相对较大的波动。由图6可见,在KB/2<0.7范围内垂荡阻尼系数呈抛物线型变化,峰值约为0.001 5,对应相对板长KB/2=0.3。当KB/2>0.7,阻尼系数随相对板长的增加而增加,并且板的倾斜角度越大,阻尼系数增加幅度越大。当α=5°时,阻尼系数保持在0.000 5以下,而当α=10°时,阻尼系数最大约为0.001 5,近似为α=5°时的3倍。当α=25°时,阻尼系数最大可达0.006 5,近似为α=5°时的13倍。另外一个值得注意的现象是当KB/2=0.75时,垂荡方向的阻尼系数为0,此时达到结构的共振频率。

图5 垂荡附加质量Fig.5 Added mass for heave

图6 垂荡阻尼系数Fig.6 Damping for heave

图7 横摇附加质量Fig.7 Added mass for roll
图7和图8为横摇方向的附加质量与阻尼系数结果。由图可见,横摇方向的附加质量和阻尼系数变化规律同横荡方向类似。横荡和横摇方向的附加质量和阻尼系数出现极值所对应的波浪频率相同。横摇附加质量在KB/2=0.2达到峰值0.049,阻尼系数在KB/2=0.5达到峰值0.017。在整个频率范围内,增加板的倾角会令横摇附加质量有所增加;但倾角的改变只会对0.2 图8 横摇阻尼系数Fig.8 Damping for roll 对比图3~8的结果可知,横荡方向附加质量和阻尼系数最大,是控制性方向。 本文利用边界单元法,研究了水下双斜板结构辐射运动时的附加质量和阻尼系数,讨论了相对板长和倾斜角度对其的影响,研究发现: 1) 横荡方向的附加质量和阻尼系数最大,是控制性方向。 2) 垂荡方向对板倾斜角度的变化最为敏感,改变倾斜角度,垂荡方向的附加质量和阻尼系数变化最大。 3) 横荡和横摇方向的附加质量和阻尼系数出现极值所对应的波浪频率相同。 [1]刘城, 洪明, 刘晓冰. 有限元/间接边界元法求解浸水板振动特性[J]. 哈尔滨工程大学学报, 2014, 35(4): 395-400, 431. LIU Cheng, HONG Ming, LIU Xiaobing. The solution for vibration characteristics of submerged plates by applying FEM/BEM[J]. Journal of Harbin Engineering University, 2014, 35(4): 395-400, 431. [2]朱航, 欧进萍. 深吃水半潜式平台垂荡响应数值分析[J]. 哈尔滨工程大学学报, 2011, 32(5): 589-594. ZHU Hang, OU Jinping. Numerical simulation of the heave motion of a deep draft semi-submersible platform[J]. Journal of Harbin Engineering University, 2011, 32(5): 589-594. [3]滕斌, 郑苗子, 姜胜超, 等. Spar平台垂荡板水动力系数计算与分析[J]. 海洋工程, 2010, 28(3): 1-8. TENG Bin, ZHENG Miaozi, JIANG Shengchao, et al. Calculation and analysis of the hydrodynamic coefficients of heave-plates of Spar platform[J]. The ocean engineering, 2010, 28(3): 1-8. [4]吴维武, 缪泉明, 匡晓峰, 等. Spar平台垂荡板受迫振荡水动力特性研究[J]. 船舶力学, 2009, 13(1): 27-33. WU Weiwu, MIAO Quanming, KUANG Xiaofeng, et al. Research on hydrodynamic characteristics of forced oscillation heave damping plates of Spar platforms[J]. Journal of ship mechanics, 2009, 13(1): 27-33. [5]康海贵, 王科. 潜型水平板水动力特性的数值研究[J]. 海洋通报, 2002, 21(1): 1-8. KANG Haigui, WANG Ke. Numerical investigation on submerged horizontal plate[J]. Marine science bulletin, 2002, 21(1): 1-8. [6]张升明. 水下板架振动的附加质量系数[J]. 水动力学研究与进展, 1990, 5(1): 88-95. ZHANG Shengming. Added mass of underwater plate and beam stiffened plate in vibration[J]. Journal of hydrodynamics, 990, 5(1): 88-95. [7]AN S, FALTINSEN O M. An experimental and numerical study of heave added mass and damping of horizontally submerged and perforated rectangular plates[J]. Journal of fluids and structures, 2013, 39: 87-101. [8]SINHA J K, SINGH S, RAO A R. Added mass and damping of submerged perforated plates[J]. Journal of sound and vibration, 2003, 260(3): 549-564. [9]SHAW D C. Perturbational results for diffraction of water-waves by nearly-vertical barriers[J]. IMA journal of applied mathematics, 1985, 34(1): 99-117. [10]MANDAL B N, CHAKRABARTI A. A note on diffraction of water waves by a nearly vertical barrier[J]. IMA journal of applied mathematics, 1989, 43(2): 157-165. [11]MANDAL B N, KUNDU P K. Scattering of water waves by a submerged nearly vertical plate[J]. SIAM journal on applied mathematics, 1990, 50(5): 1221-1231. [12]PARSONS N F, MARTIN P A. Scattering of water waves by submerged curved plates and by surface-piercing flat plates[J]. Applied ocean research, 1994, 16(3): 129-139. [13]MIDYA C, KANORIA M, MANDAL B N. Scattering of water waves by inclined thin plate submerged in finite-depth water[J]. Archive of applied mechanics, 2001, 71(12): 827-840. [14]KHARAGHANI S, LEE J J. Wave interaction with moored sloping breakwater[C]//Proceedings of the 20th International Conference on Coastal Engineering. Taiwan, 1986: 2259-2268. [15]SOBHANI S M, LEE J J, WELLFORD L C. Interaction of periodic waves with inclined portable barrier[J]. Journal of waterway, port, coastal and ocean engineering, 1988, 114(6): 745-761. [16]CHO I H, KIM M H. Wave absorbing system using inclined perforated plates[J]. Journal of fluid mechanics, 2008, 608: 1-20. [17]NEWMAN J N, LEE C H. Boundary-element methods in offshore structure analysis[J]. Journal of offshore mechanics and arctic engineering, 2002, 124(2): 81-89. [18]滕斌, 金瑞佳, 勾莹. 波浪力计算中高阶边界元的改进方法[J]. 哈尔滨工程大学学报, 2012, 33(11): 1321-1325. TENG Bin, JIN Ruijia, GOU Ying. An improved method for the calculation of wave force by HOBEM[J]. Journal of Harbin engineering university, 2012, 33(11): 1321-1325. [19]WANG Ke, ZHANG Zhiqiang, XU Wang. Transmitted and reflected coefficients for horizontal or vertical plate type breakwater[J]. China ocean engineering, 2011, 25(2): 285-294. [20]WANG Ke, ZHANG Xi, GAO Xin. Study on scattering wave force of horizontal and vertical plate type breakwaters[J]. China ocean engineering, 2011, 25(4): 699-708. Hydrodynamic coefficients of the radiation problem of double submerged inclined plates ZHANG Zhiqiang1, LUAN Maotian1, WANG Ke2 (1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China; 2. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China) In this paper, the added mass and damping coefficients of a submerged structure that consists of two inclined rigid thick plates were studied. The adopted boundary element method in the research can be flexibly applied to submerged double inclined plates with any thickness and any inclined angle. Results indicate that the added mass and damping of sway are the largest, heave is the most sensitive to the change of inclined angle, and the wave frequencies of the maximal value of added mass and damping for sway and roll are the same. submerged double inclined plates; boundary element method; added mass; damping coefficient 2015-06-08. 时间:2016-12-12. 国家重点基础研究发展计划项目(2013CB036101). 张志强(1984-), 男, 博士研究生; 王科(1970-), 男, 副教授,博士; 栾茂田(1962-), 男,教授,博士生导师. 王科,E-mail:kwang@dlut.edu.cn. 10.11990/jheu.201506024 U661.1 A 1006-7043(2017)01-0048-06 张志强,栾茂田,王科水下双斜板结构辐射问题的水动力系数研究 [J]. 哈尔滨工程大学学报, 2017, 38(1): 48-52,94. ZHANG Zhiqiang, LUAN Maotian, WANG Ke. Hydrodynamic coefficients of the radiation problem of double submerged inclined plates[J]. Journal of Harbin Engineering University, 2017, 38(1): 48-52,94. 网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20161212.1631.024.html
5 结论
