考虑通信时延的船舶航向保持鲁棒自适应控制

徐国平，张显库，张国庆

(大连海事大学 航海学院，辽宁 大连116026)

考虑通信时延的船舶航向保持鲁棒自适应控制

徐国平，张显库，张国庆

(大连海事大学 航海学院，辽宁 大连116026)

为了进一步研究船舶航向保持远程控制，本文提出一种鲁棒自适应神经网络控制方案以解决网络诱导时延对系统稳定性和性能的不良影响。与传统Backstepping方法不同，该方案将系统不同阶子系统中的不确定部分纵向传递至第n个子系统，并利用径向基函数神经网络进行在线逼近，达到对系统中模型不确定部分的有效补偿，从而解决远程控制系统中不确定时延问题。通过实际测试分析海事卫星通信网络时延特性，以“育鲲”轮为例开展仿真试验，结果验证了本文算法的有效性，且对模型摄动和外界环境干扰具有较好的鲁棒性能。该算法具有计算量小、鲁棒性强、易于工程应用的优点。

船舶；航向保持；Backstepping；鲁棒自适应控制；网络控制系统；卫星通信时延

21世纪，随着计算机、控制、传感器和通信技术的快速发展，水面无人船(unmanned surface vehicle,USV)的研究和应用也得到了迅速发展。2014年，劳斯莱斯公司宣布将在十年之内研制成无人货船并可进行远程操控。船舶实现无人驾驶或远程操控，关键技术在于船舶运动控制的智能化和网络化。近年来，网络控制系统(networked control system,NCS)在船舶自动航行装备中的应用已引起不少学者的关注[1-2]。船舶实现网络远程控制必定涉及卫星通信，其中网络诱导时延问题不可避免，而且不同于常规控制系统中的时延，需要特殊考虑处理。针对网络时延和控制系统的性能要求，许多研究人员提出了各种控制方法，以减小网络时延的影响或对网络时延进行有效地补偿。

实际NCS具有时延是普遍的，而且通常时延具有不确定性，如果设计时忽视时延的影响，可能会导致系统不稳定。文献[3]运用增广状态向量法，将具有时延的闭环系统变成一个无时延的时变系统或定常系统。该方法直观易于理解，并且结构简单容易工程实现，但只适用于具有周期性时延的NCS。文献[4]通过设计一个时延补偿器来补偿时延对系统的影响，将时变系统转化为时不变系统。该方法进一步拓展了时延补偿器的应用范围，可用于具有有界非周期性时延的NCS。文献[5]中提出了一种基于Lyapunov稳定性理论和线性矩阵不等式技术的、考虑系统有限时间控制性能的动态反馈控制方法。尽管该方法简单易行，由于Lyapunov-Krasovskii能量函数和对其泛函的求导过程必然导致最终得到的控制律极度复杂甚至难以获得，即复杂度爆炸问题。文献中对于该类问题进行了线性处理，通过构建鲁棒控制保证了整个闭环系统控制性能，这也导致最终设计结果具有一定的保守性。针对以上问题，文献[6]进一步提出一种改进的Wirtinger不等式设计方法以降低执行控制律的保守性。

为了解决针对时延非线性系统中复杂度爆炸问题，文献[7]针对一般严反馈系统给出了一种自适应动态面控制技术，避免了不同自由度虚拟控制的反复求导，一定程度上解决了该类问题。与此类似，文献[8]则在原有算法的基础上引入了连续封装函数和双曲正切函数，避免了对虚拟控制律的反复求导，最终达到对时延不确定的有效补偿。

综上所述，本文试图基于自适应神经网络方法，从根源上解决复杂度爆炸问题。该算法不同于传统的Backstepping方法。首先将每一子系统中时延不确定部分纵向传递至第n个子系统，然后只需在实际控制律中引入单一径向基神经网络进行在线补偿，避免随着系统维数增加导致需要在线学习的神经网络过多，以致算法难以工程应用。基于船舶远程航向保持控制系统进行了仿真实验。

1 问题描述

海事卫星是集全球海上常规通信、遇险与安全通信、特殊与战备通信于一体的实用性高科技产物。海事卫星已升级到符合3G标准的第四代系统，全面兼容WCDMA 3G标准。Inmarsat公司是目前唯一提供全球范围内卫星移动通信的运营商，推出了先进通信功能的宽带全球区域网络(broadband global area network,BGAN)系统。图1给出了基于BGAN网络的船舶远程遥控逻辑结构图。

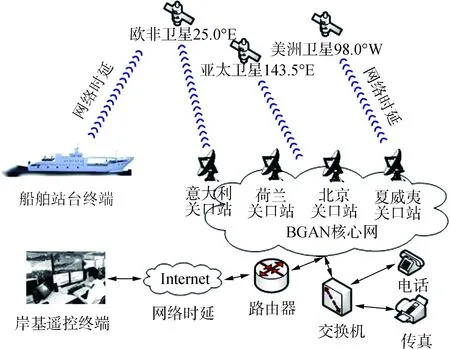
图1 基于BGAN网络的船舶远程遥控结构图Fig.1 The basis diagram for ship remote control by employing the BGAN network

本文研究从实际问题出发，首先对海事卫星通信网络的传输时延性能进行实际测试，通过分析卫星通信时延特性，同时考虑船舶航向保持的非线性，提出一种鲁棒自适应神经网络控制方案，从而解决此类具有不确定时延的一般严格反馈系统的鲁棒自适应控制问题。本节通过两种方式对海事卫星通信网络的传输时延性能进行测试。

第一种方式是通过船舶上实际装备的Globe iFusion系统，在航行中分别测试不同海域船舶节点至大连和北京某节点的往返时延(round trip time,RTT)性能。具体测试情况见表1。

第二种方式是通过实验室的BGAN Explorer 710设备，测试其到大连和北京某节点之间的RTT性能,测试时选择标准IP数据。

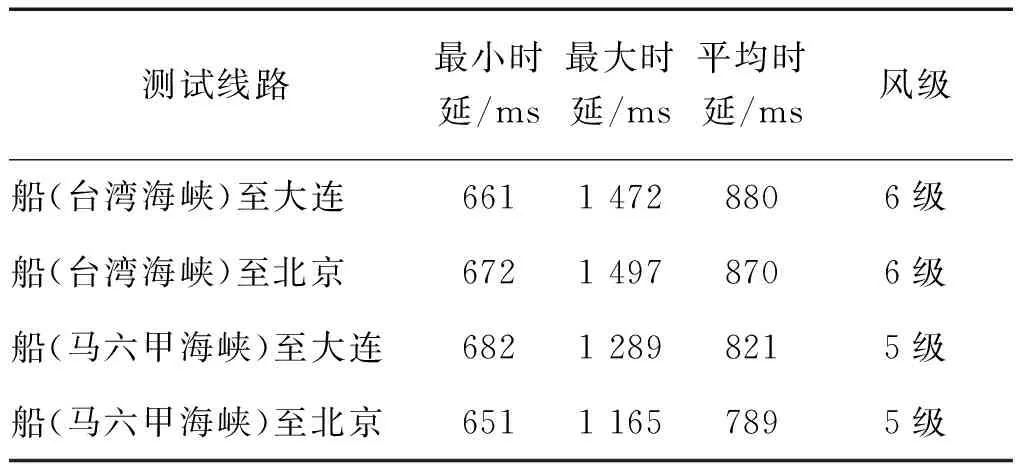
表1 Globe iFusion RTT性能测试

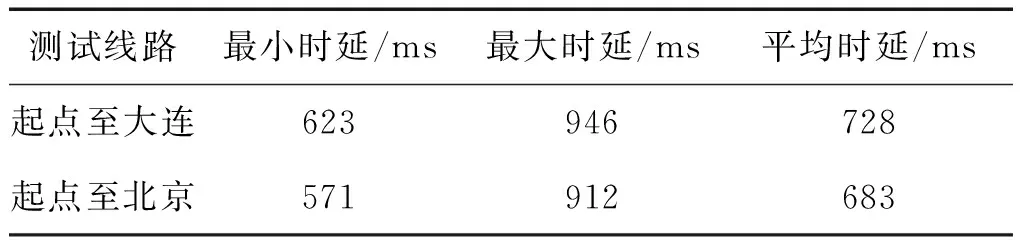
表2 BGAN Explorer 710 RTT性能测试

由表1和表2可以看出海事卫星通信网络时延具有不确定性，同时考虑船舶航向保持的非线性，因此研究如下具有不确定时延的一般严格反馈系统：

(1)

假设1 未知虚拟控制增益函数gi(·)仅限于在一定的范围内，如

(2)

(3)

定理1[9](万能逼近定理)：一定存在给定的NNs和ε>0，满足

(4)

(5)

定义1

(6)

例如：K2,1=k1+k2;K3,2=k1k2+k2k3+k1k3满足：

(7)

2 控制器设计

本文首先利用Backstepping设计方法将第n步之前的未知非线性项纵向传递到第n步，通过构造Lyapunov-Krasovskii函数对不确定时延进行补偿，然后再用RBF NNs进行逼近，以达到对系统不确定时延的有效镇定。为了应用Backstepping方法设计控制器，做如下坐标变换：

(8)

式中αi-1,(i=2,…,n)为第(i-1)步中的虚拟控制变量。

2.1 设计第1步

首先对变量z1求导数得

(9)

定义Lyapunov函数Vz1为

(10)

由假设3可得不等式关系(11)用于后续控制器设计分析：

(11)

为了处理式(9)中的不确定时延项，在式(10)的基础上进一步构建Lyapunov-Krasovskii函数为

(12)

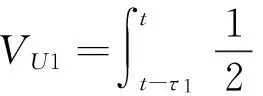
结合式(9)和(11)，对Lyapunov-Krasovskii函数V1进行求导，并整理为

(13)

根据Lyapunov稳定性理论，选取式(14)所示的虚拟控制量α2:

(14)

式中：k1>0为设计参数。

将式(14)代入式(13)可整理得

(15)

因此，第2个误差变量z2可表示为

(16)

式中：K1,1=k1,F1(·)=F1(x1)。

2.2 设计第i(2≤i≤n-1)步

第i步误差变量zi为

(17)

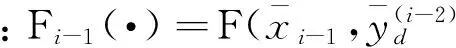
(18)

与第1步类似，选取Lyapunov-Krasovskii函数Vi为

(19)

(20)

其中，

(21)

对Vi进行求导，进一步可整理出：

(22)

(23)

根据式(22)的补偿需求，构建虚拟控制变量αi+1为

(24)

其中:ki>0为设计参数。

为了进一步完成控制器设计，根据定义1通过演绎可得到对等关系:

(25)

结合式(24)和式(25)整理得第i+1个误差变量zi+1为

(26)

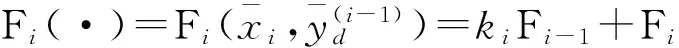
2.3 设计第n步

为了能够获取实际系统可执行的控制律，接下来的设计首先按照上述方式演绎出不确定系统所需的期望控制器，然后利用RBF NNs逼近n阶子系统累加未知非线性项Fn(·)，最终获取可实际执行的控制律。

(27)

其中，

(28)

选取Fn(·)用于描述式(29)所示的非线性部分。

(29)

因此，设计对非线性时延系统产生有效补偿的期望控制输入为

(30)

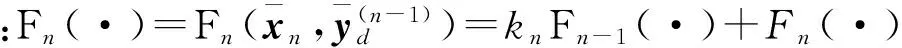
(32)

其中，Γ=ΓT>0,ρ>0均为参数矩阵。

3 稳定性分析

证明：构建整个闭环控制系统的Lyapunov-Krasovskii函数如式(33)所示

(33)

根据Young’s不等式，可以得到以下放缩关系用于整个系统的稳定性分析：

(34)

对Lyapunov-Krasovskii函数V进行求导可得

(35)

通过适当调整设计参数，可以保证满足式(36)的关系。

(36)

因此，式(35)可进一步整理为

(37)

基于Lyapunov稳定性理论，易证整个闭环系统中所有变量满足半全局一致最终有界。

4 仿真实验及结果分析

(38)

图2(a)给出了表1中船舶在台湾海峡时至北京的网络时延实际测试结果，图2(b)给出了该仿真实验中对672～1 497 ms不确定时延的模拟结果。通过对比可知，仿真实验中对不确定时延的模拟与实测时延非常相近。通过以上模拟构建卫星通信网络环境以对本文所提算法进行测试，具有一定的可信性。

(a)船(台湾海峡)至北京实测网络时延

(b)672～1 497 ms的模拟结果图2 表1中船台湾海峡至北京网络时延模拟对比结果Fig.2 Comparison of the practical time delay, i.e. network delay from the ship station to Beijing in Table 1 and the simulated one

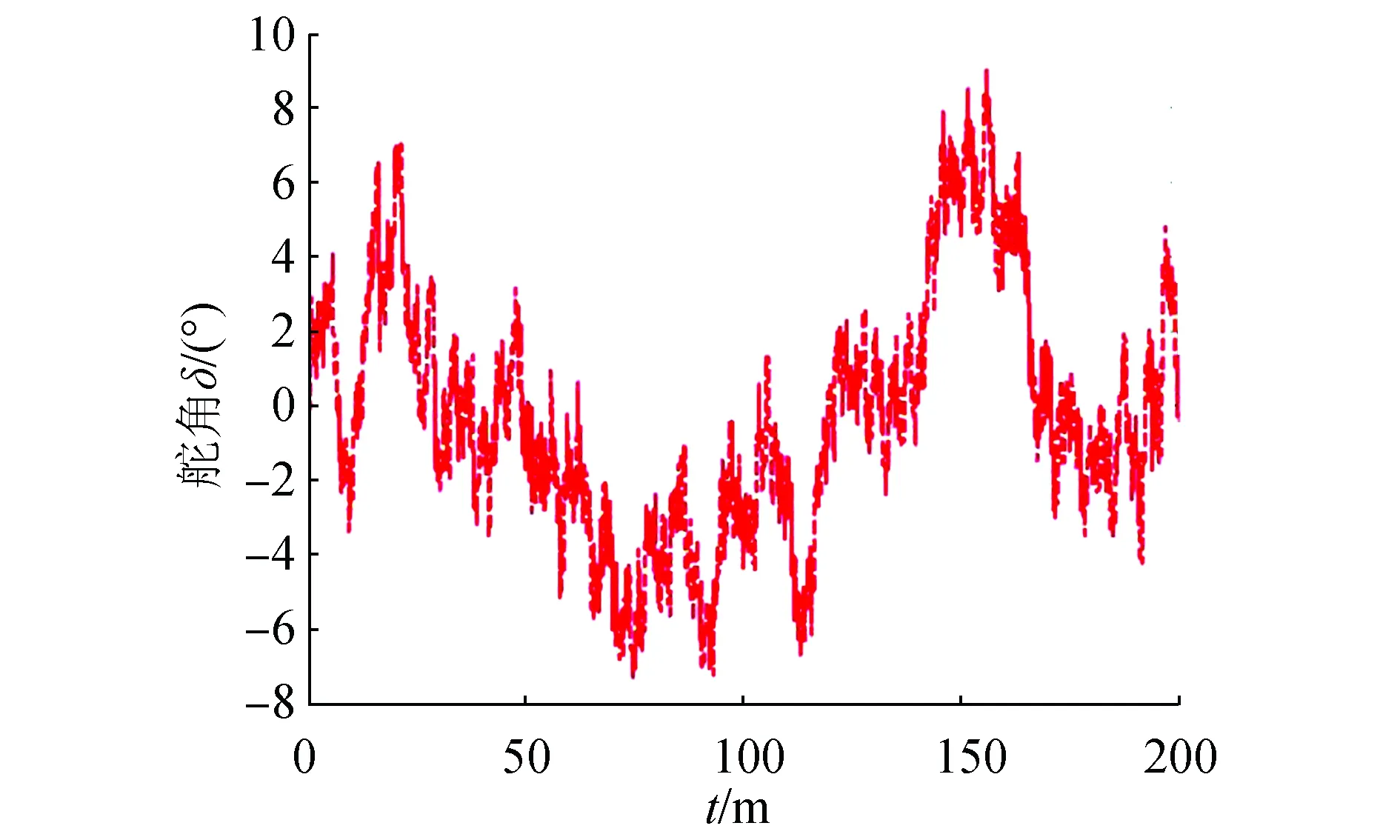
图3 6级海洋环境干扰等效舵角模拟Fig.3 The equivalent rudder angle describing the environment disturbance

为了验证该算法的有效性，该实验中对比控制器为式(38)中去掉NNs补偿后的控制律。图3为仿真实验过程中利用马尔科夫过程描述的6级海洋环境干扰等效舵角情况。图4(a)和(b)给出6级海况下不同时延条件时船舶航向曲线和舵角曲线。仿真结果显示，本文所提算法能够有效抑制系统状态变量测量时延和模型不确定的影响，在不同时延条件下航向跟踪控制效果基本不变。该实验中，船舶输出航向均能够在70 s以后稳定，最终无静差地跟踪参考航向。去掉控制律中单一神经网络补偿后，船舶航向保持控制进入稳态后存在一定静差，而需求控制舵角能量基本不变。图5给出了神经网络权重在线学习情况。可以看出，神经网络能够随着闭环系统趋于稳定完成对网络权重的在线学习，最终趋于稳定，通过逼近模型中时延非线性部分实现对系统中状态变量测量时延的有效补偿。以上结果验证了本文中鲁棒自适应控制策略的有效性。

(a)船舶的输出航向

(b)船舶的控制舵角图4 6级海况下船舶航向保持控制结果(具有不同网络时延)Fig.4 The simulation result with the different time delaysunder the 6thsea states

图5 神经网络权重在线学习曲线Fig.5 The updated curve for the neural network weights

5 结论

通过实际测试分析海事卫星通信网络时延特性，以大连海事大学科研实习船“育鲲”轮作为被控对象进行仿真试验。结果表明，在恶劣海况下，该控制策略能够有效补偿系统状态反馈通信时延的影响，对模型摄动和外界干扰具有较好的鲁棒性能。 该算法具有计算量小、易于工程应用的优点，对海上船舶通过海事卫星进行远程操纵具有重要的现实工程意义。

[1] YIN Yin, REN Zhengying, SONG Lizhong, et al. The networked controller design over the ship IPMS network[C]//Proceedings of International Conference on Modelling, Identification & Control. Wuhan, China: IEEE, 2012: 725-730.

[2]冯宜伟, 郭戈. 基于网络的船舶航向控制器设计[J]. 兰州理工大学学报, 2010, 36(5): 73-78. FENG Yiwei, GUO Ge. Network-based controller design for ship course control[J]. Journal of Lanzhou university of technology, 2010, 36(5): 73-78.

[3]HALEVI Y, RAY A. Integrated communication and control systems: part I-analysis[J]. Journal of dynamic systems, measurement, and control, 1998, 110(4): 367-373.

[4]RAY A, HALEVI Y. Integrated communication and control systems: part II-design considerations[J]. Journal of dynamic systems, measurement, and control, 1998, 110(4): 374-381.

[5] LIU Hao, ZHAO Xudong. Finite-time H∞control of switched systems with mode-dependent average dwell time[J]. Journal of the franklin institute, 2014, 351(3): 1301-1315.

[6]刘于之, 李木国, 杜海. 具有时延和丢包的NCS鲁棒H∞控制[J]. 控制与决策, 2014, 29(3): 517-522. LIU Yuzhi, LI Muguo, DU Hai. Robust H∞ control of NCS with delay and packet dropout[J]. Control and decision, 2014, 29(3): 517-522.

[7]LI Yongming, LI Tieshan, TONG Saocheng. Adaptive dynamic surface control of uncertain nonlinear time-delay systems based on high-gain filter observer and fuzzy neural networks[M]. Berlin Heidelberg: Springer, 2012: 416-423.

[8]HE Chao, LI Junmin, ZHANG Lin. Decentralized adaptive control of nonlinear large-scale pure-feedback interconnected systems with time-varying delays[J]. International journal of adaptive control and signal processing, 2015, 29(1): 24-40.

[9]GE S S, HANG C C, LEE T H, et al. Stable adaptive neural network control[M]. Nowell, USA: Kluwer Academic Publishers, 2002.

[10]赵园, 郭戈, 丁磊, 等. 舰船编队的避障/避碰控制[J]. 信息与控制, 2012, 41(4): 425-432, 438. ZHAO Yuan, GUO Ge, DING Lei, et al. Collision/obstacle avoidance control of vessel formation[J]. Information and control, 2012, 41(4): 425-432, 438.

[11]ZHANG Guoqing, ZHANG Xianku, XU Guoping. A novel concise adaptive neural control for a class of nonlinear MIMO systems with unknown time delays[J]. Journal of computers, 2014, 9(1): 65-71.

[12]张显库, 金一丞. 控制系统建模与数字仿真[M]. 2版. 大连: 大连海事大学出版社, 2013. ZHANG Xianku, JIN Yicheng. Control system modeling and numerical simulation[M]. 2nd ed. Dalian: Dalian Maritime University Press, 2013.

Robust adaptive control for ship course-keeping by considering communication delay

XU Guoping,ZHANG Xianku,ZHANG Guoqing

(College of Navigation, Dalian Maritime University, Dalian 116026, China)

To study remote control for ship course-keeping, a new robust adaptive neural network algorithm was developed to solve the adverse effects of network-induced delay on system stability and performances. Unlike in the traditional backstepping method, the proposed scheme longitudinally transfers the uncertain part in different orders of subsystems of the system to thensubsystem. In addition, the neural network of radial basis function was employed to carry out online approximation to effectively compensate for the uncertain model part in the system and solve the problem of uncertain time delay in the remote control system. In the simulation test, the time delay characteristics were obtained by analyzing an actual test of a maritime satellite communication network, and the YUKUN ship was selected as the plant. Results verify the effectiveness of the algorithm. In addition, the algorithm has good robustness against model perturbation and external disturbance. The algorithm has the advantages of a small amount of calculation, good robustness, and easy engineering application.

ship; course-keeping; backstepping; robust adaptive control; networked control system; satellite communication delay

2015-09-06.

时间：2016-12-12.

国家自然科学基金项目(51679024)；中国博后创新人才支持计划(BX201600103)；中央高校基本科研业务费专项资金(3132016315, 3132016001).

徐国平(1980-),男,博士研究生; 张显库(1968-),男,教授,博士生导师.

张显库,E-mail:zhangxk@dlmu.edu.cn.

10.11990/jheu.201509015

U666

A

1006-7043(2017)01-0059-07

徐国平，张显库，张国庆.考虑通信时延的船舶航向保持鲁棒自适应控制[J]. 哈尔滨工程大学学报， 2017, 38(1): 59-65. XU Guoping,ZHANG Xianku,ZHANG Guoqing.Robust adaptive control for ship course-keeping by considering communication delay[J]. Journal of Harbin Engineering University,2017, 38(1): 59-65.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.0920.006.html