基于相干干扰抑制的时域恒定束宽波束形成

黄聪, 李迪

(1.中国舰船研究设计中心，湖北 武汉 430064；2.武昌船舶重工有限责任公司，湖北 武汉 430064)

基于相干干扰抑制的时域恒定束宽波束形成

黄聪1, 李迪2

(1.中国舰船研究设计中心，湖北 武汉 430064；2.武昌船舶重工有限责任公司，湖北 武汉 430064)

基于相干干扰抑制的时域恒定束宽波束形成，通过对恒定束宽波束的干扰方位上设计零陷，在时域上实现了宽带信号的高精度获取和固定方向的相干干扰抑制。时域波束形成的分步设计法分为波束优化的权值设计和FIR滤波器的系数设计两个步骤。由于分步设计法无法获得全局最优，所以得到的时域波束旁瓣和零陷的性能有所下降。本文针对分步设计法的缺陷，提出了一种基于全局设计的改进方法。该方法将波束优化的权值设计与滤波器的系数设计进行联合求解，提高了时域波束的设计精度，有利于弱信号的检测和参数估计。通过计算机仿真和水池试验验证了该方法的有效性。

恒定束宽；相干干扰抑制；波束形成；FIR滤波器；二阶锥规划；阵列信号处理

在利用目标辐射信号或目标回波进行参数估计时，通过宽带波束形成获得高信噪比且不失真的有效信号尤为重要。在固定的阵列形状下，常规波束形成的主瓣宽度会随频率的增加而变窄，当入射角度偏离波束的主轴时，信号的幅度响应会随频率的增大而减小。为了获得精确的宽带信号需要对每个频点进行恒定束宽的波束优化。由于频域波束形成难以获得准确连续的宽带时域信号，实时性受限，且时频转换带来了能量损失，所以想要获得高精度的时域信号，常用时域FIR滤波器来实现恒定束宽的波束形成。

鉴于恒定束宽频域波束优化的权值设计已趋成熟，研究重点便成了如何设计时域的FIR滤波器系数，使滤波器的频率响应逼近频域的优化权值。Frost等[1]提出了线性约束自适应波束形成方法，采用约束最小均方误差的方法使FIR波束形成器在期望方向上形成阵列响应，最大限度抑制其他方向的噪声和干扰，但要求期望信号到达各阵元FIR滤波器的输入端时必须同相，这在工程应用中很难实现。Godara[2]推导出了FIR波束形成器中各阵元所对应的滤波器系数与频域中各阵元子带的权值互为傅里叶变换对，但是滤波器的长度必须等于权值设计的频点数，且FIR滤波器系数仅单纯通过频域权值的逆傅里叶变换得到，而频域与时域转换将产生能量泄漏，导致设计的误差增大。鄢社锋等[3]提出了基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成，分别利用二阶锥规划设计出每个频点的恒定束宽权值和满足频域权值的时域FIR滤波器系数。

本文研究了基于FIR滤波器的时域波束形成实现方法，利用FIR滤波器来实现宽带信号每个频点的加权时域波束形成，在时域上实现了波束的恒定束宽以及相干干扰抑制[4-8]。针对分步设计法时域波束旁瓣和零陷设计精度下降的缺陷，给出了一种基于相干干扰抑制的全局约束设计方法，并将其应用于多普勒频偏估计中的波束接收中。

1 波束优化的权值设计

波束图优化的目的是对波束图进行优化以满足实际的应用要求，而波束设计的关键便是求解最优的阵列权值。波束图的综合设计主要包括波束指向、主瓣设计精度、旁瓣级、零陷深度、权值范数等的约束。先给出恒定束宽波束优化的统一表达式：

(1)

式中：θ0表示波束的期望方向，θML表示波束主瓣的方向，θSL表示波束旁瓣的方位，θNL表示波束零陷的方位，pd(θML)表示期望波束的主瓣响应，ξ1为主瓣精度的约束，ξ2为旁瓣级的约束，ξ3为零陷深度的约束，ξ4为加权向量范数的约束。

由式(1)中可以看出，波束的设计是在主瓣区间θML的波束响应与期望的波束响应pd(θML)误差最小的情况下，保证期望方向θ0的波束响应无失真，对旁瓣区间θSL的旁瓣级和加权向量w的范数进行约束。使每个频点波束的主瓣响应都逼近期望的波束响应pd(θML)，从而使波束宽度不随频率变化。由于式(1)满足二阶锥规划[9-12]的标准表达式，可以利用二阶锥规划的方法来求解波束设计的优化权值w，且该优化方法适用于任意的阵列形状。

2 基于FIR滤波器的时域波束优化

为了实现宽带恒定束宽的时域波束形成，需要使FIR滤波器的频率响应逼近阵列优化权值的频率响应。根据阵列流形设计出宽带信号每个频点的恒定束宽波束优化权值：

(2)

式中：w的每一列为单个频点的优化权值，每一行为单路信号的滤波器期望响应，核心问题是利用FIR滤波器来对单路信号的滤波器期望响应进行逼近。

2.1 基于二阶锥规划的滤波器分布设计法

为了进一步提高FIR滤波器系数的设计精度，鄢社锋等[1]提出了基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成。该方法将恒定束宽的FIR时域波束形成分为单个频点的恒定束宽波束优化的权值设计与FIR滤波器的系数设计这两个步骤，也被称为分步设计法，流程如图1所示。

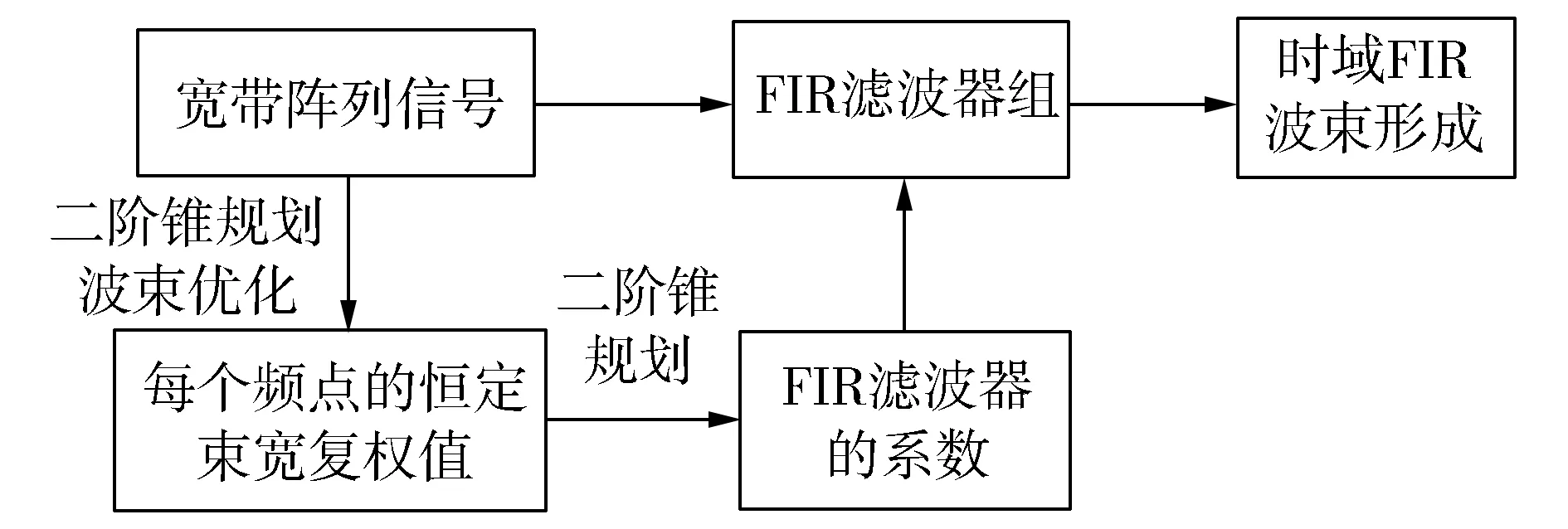
图1 基于二阶锥规划的FIR恒定束宽波束形成流程图Fig.1 The flow chart of FIR filter constant beamwidth beamforming based on second-order cone programming

宽带时域波束形成同样存在相干干扰的问题。假设波束的主轴方向为110°，相干干扰的方向为43°，在恒定束宽的波束上同样设计区间为40°～45°的零陷，零陷深度为-70 dB。频域设计的恒定束宽波束图如图2所示。

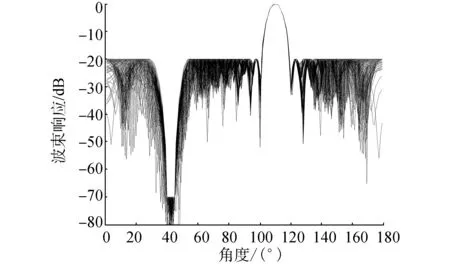
图2 频域设计恒定束宽波束图Fig.2 The beam of constant beamwidth designed in frequency domain

图3 时域恒定束宽波束图Fig.3 The beam of constant beamwidth designed in time domain

利用图1中的分布设计法实现时域恒定束宽波束图，仿真结果如图3所示。其中滤波器的阶数为64阶，由于FIR滤波器的设计误差，导致时域波束上的零陷提高至约-45 dB，相干干扰的抑制能力下降。

2.2 基于二阶锥规划的滤波器全局约束法

分步法的设计把恒定束宽时域波束形成分为子带的频域波束优化设计和FIR滤波器系数的优化设计，两个步骤都可以转化二阶锥规划问题求解，但是只能确保两者分别是最优的。在频域上设计每个频点的波束图满足零陷的要求，但是FIR滤波器设计误差导致零陷的提升。为了克服分步法只能在两个步骤上分别得到最优解的缺陷，下面给出全局约束的FIR滤波器设计，将波束优化与滤波器系数的设计进行联合求解，得到全局最优的滤波器系数，这样可以更好地控制波束的旁瓣和零陷。

假设第m号阵元的FIR滤波器的系数hm为

(2)

则所有阵元的FIR滤波器的系数矩阵H为

(3)

滤波器的频率响应Hm(f)为

(4)

其中，e(f)=[1 e-j2πfTs… e-j2πf(L-1)Ts]T。若第m号阵元先进行Tm的整数时延，并同时加入FIR滤波器的群时延，则可以得到FIR滤波器第m号阵元的频率响应为

(5)

在单个频点上的等效频域权值为

(6)

式中:κ(f)=[κ1(f) …κm(f) …κM(f)]T为Hadamard积。

则利用FIR时域波束形成得到的波束响应p(f,θ)为

(7)

其中，a(f,θ)为阵列流形矢量。为了简化二阶锥规划的设计，将FIR的滤波器系数矩阵重排为一个列向量h

(8)

则波束响应p(f,θ)可以改写为

(9)

式中u(f,θ)=e(f)⊗[a(f,θ)∘κ(f)]，符号⊗表示Kronecker积。

式(9)直接建立了FIR滤波器系数与每个频点波束图的关系，可以通过对波束图的约束直接对FIR的滤波器系数矩阵进行优化设计，得到全局最优的滤波器系数，这样可以更好地控制波束的旁瓣和零陷，但是由于一次性设计出所有的FIR滤波器系数，增加了二阶锥规划的计算量，其具体表达式可以表示为

(10)

与图2的频域恒定束宽设计要求相同，设计的FIR滤波器阶数为32时，给出式(10)的全局约束得到的FIR时域波束图如图4所示。可以看出在阶数为32时，便可以使时域FIR恒定波束图获得满足设计要求的旁瓣级和零陷深度，说明直接设计法可以获得全局最优的设计精度，相比分步设计法两步独立最优设计，全局约束法可以用更少的滤波器阶数获得更精确的时域FIR恒定波束图设计精度，但缺点是大大增加了二阶锥规划的运算量。

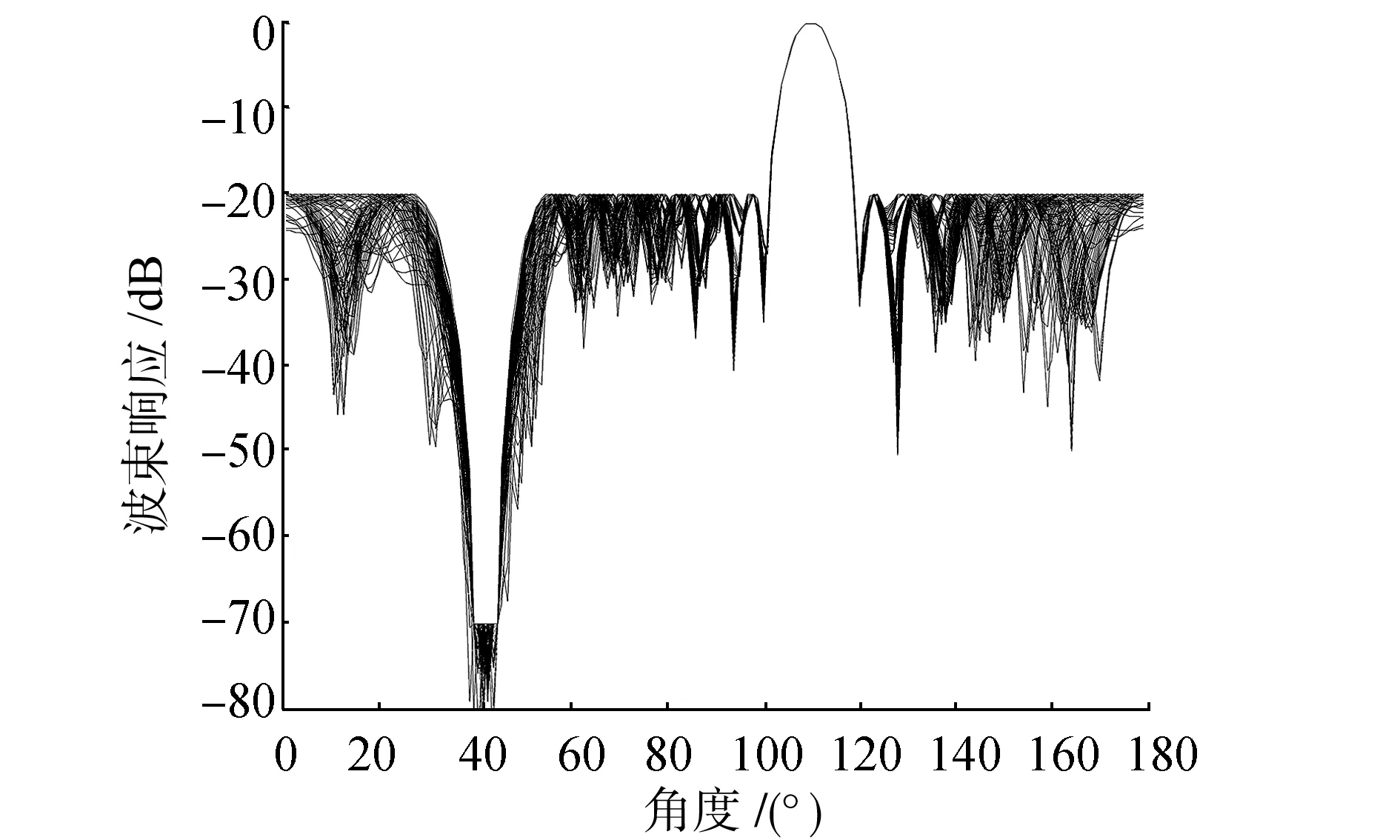
图4 时域恒定束宽波束图Fig.4 The beam of constant beamwidth designed in time domain

3 基于相干干扰抑制的弱信号提取

3.1 计算机仿真

利用图4全局约束法设计的FIR时域恒定束宽进行波束接收，波束形成的主轴方向为110°，为70～130 kHz的LFM，脉宽2 ms，持续时间约为1 000～2 000点，改变干扰信号的形式信号，干扰为70～130 kHz的LFM，脉宽4 ms，持续时间约为500～2 500点，干信比为40 dB。给出理想情况下的波束时域输出如图5所示。

(a)单阵元的接收信号

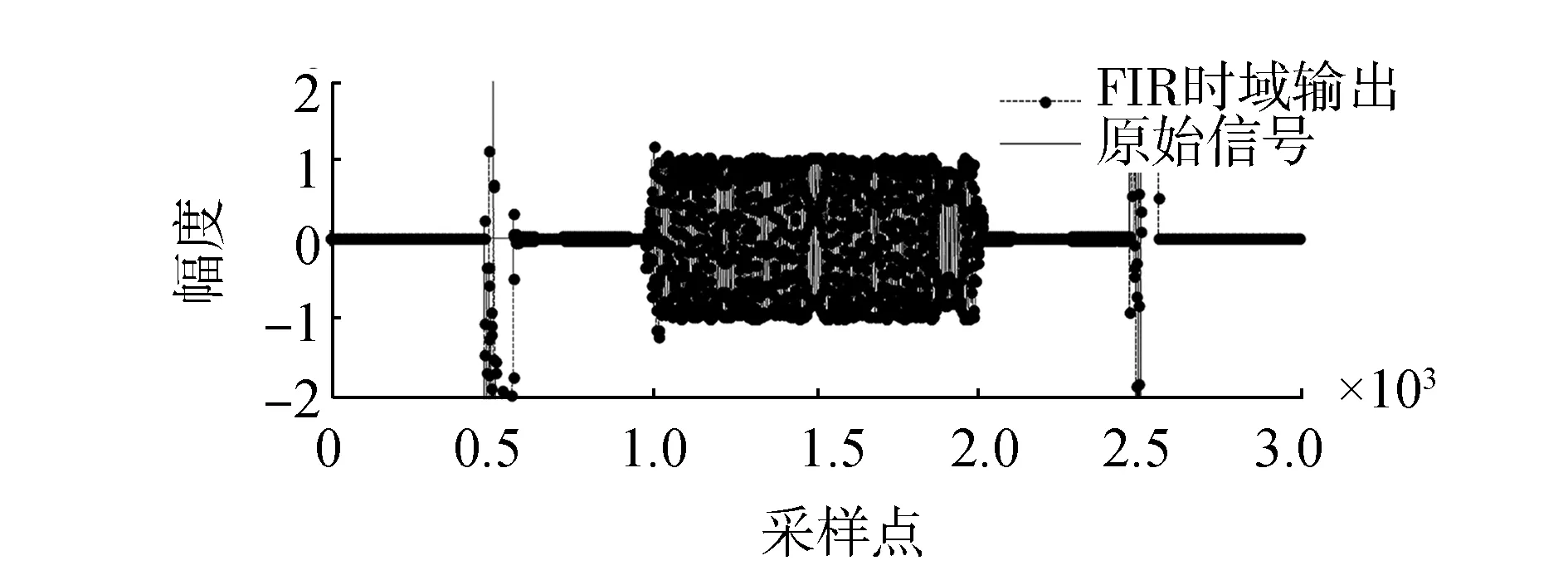
(b)波束输出信号图5 主轴方向入射的时域恒定束宽波束输出Fig.5 The beam output in the main shaft direction of constant beamwidth designed in time domain

图5(a)为单个阵元的接收信号，信号完全淹没在干扰中，(b)中的虚线为加入零陷设计的波束输出，实线为期望信号，可以看出时域FIR恒定束宽波束输出很好地抑制了零陷方向的相干干扰，实现了弱信号的提取。但是由于FIR滤波器的稳定过程，在信号干扰信号起始和结束的位置附近出现畸变。

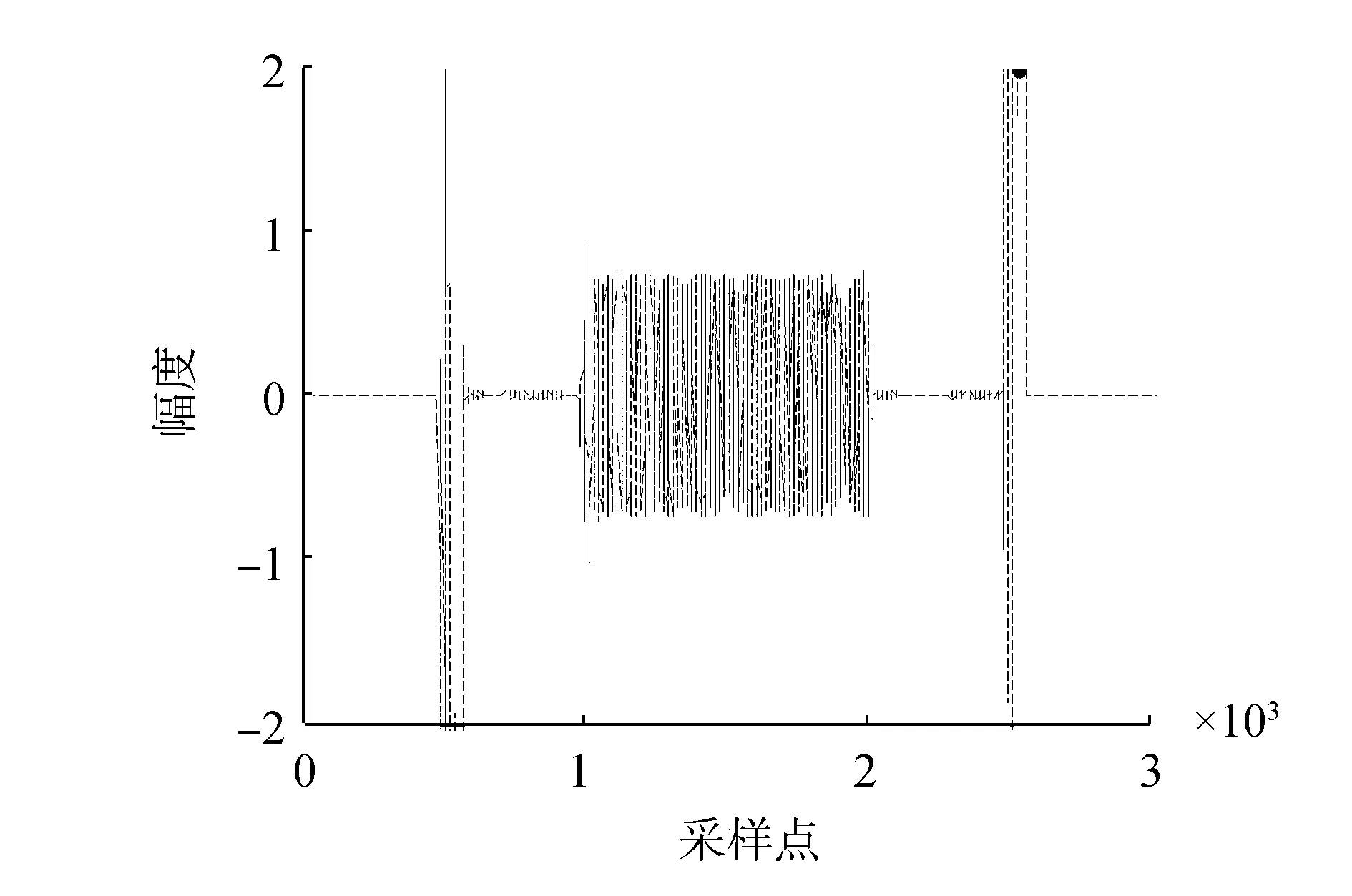
(a)偏离4°

(b)偏离3°

(c)偏离2°

(d)偏离1°图6 偏离主轴的时域恒定束宽波束输出Fig.6 The beam output deviated from the main shaft of constant beamwidth designed in time domain

假设信号的入射方向偏离主轴，相干干扰方向不变，干信比为30 dB，分别给出偏离主轴4°、3°、2°和1°时的波束输出，如图6所示。可以看出FIR时域恒定束宽在入射信号偏离主轴时，并没有发生输出信号的幅度随频率增加而减小的现象，达到了恒定束宽的效果，但是波束输出的信号增益随着偏离角度的增大而减小。

3.2 算法性能分析

时域FIR恒定束宽的波束主轴方向为110°，下面给出波束在106°～110°的主瓣内期望响应，如表1所示。

表1 主瓣内期望响应

对波束输出的信号按照表1的期望响应，对波束主瓣内入射的信号进行频域补偿，得到输出信号的均方根误差如图7和图8所示。

图7为入射信号主轴方向，在不同干信比下，输出信号的均方根误差随信噪比的变化曲线。图8为干信比40 dB时，时域波束输出进行期望响应的频域补偿后，波束主瓣内入射的波束输出信号的均方根误差随信噪比的变化曲线，可以看出进行频域补偿后，波束主瓣内入射的波束输出信号的均方根误差都非常接近，满足恒定束宽设计要求。

图7 均方根误差随信噪比的变化曲线Fig.7 The performance curves between RMSE and SNR

图8 均方根误差随信噪比的变化曲线Fig.8 The performance curves between RMSE and SNR

4 水池实验结果

水池试验采用收发合置的声呐对运动小目标回波进行检测，声源T1发射LFM脉冲对信号[13]，单个脉冲长度为2 ms，带宽为90～110 kHz，发射信号的触发周期为0.25 s。声源T2发射长脉冲的宽带相干扰。接收为16元的圆弧阵，运动目标水杯和干扰源T2都满足远场条件，目标水杯和T2相对接收阵为78°和118°，采样频率fs=500 kHz。拉动水杯做靠近接收阵方向的径向运动，通过目标水杯的回波信号来进行多普勒频偏的估计。水池试验配置如图9所示。

利用图10的时域恒定束宽波束图对目标回波进行接收，波束指向为78°，零陷区间为115°～120°，零陷深度为-60 dB。

在未放置干扰声源T2时，波束输出的信号和相关处理结果如图11所示，相关峰位置对回波信号进行截取及多普勒的频偏估计，黑框为截取的动目标回波信号，多普勒频偏估计的结果分别为27.6 Hz和27.9 Hz。目标的运动速度为0.2 m/s，对应中心频率100 kHz的多普勒频偏为26.67 Hz，与脉冲对多普勒频偏的估计值吻合。

图9 水池试验配置图Fig.9 The schematic diagram of tank experiment

图10 时域恒定束宽波束图Fig.10 The beam pattern of constant beamwidth in time domain

(a)恒定束宽的波束输出

(b)波束输出信号的相关处理图11 波束输出信号和相关处理Fig.11 The beam output signal and correlation

在相对接收阵118°的位置处放置相干干扰声源T2，发射带宽相同的LFM长脉冲，发射指向接收阵，分别给出干信比ISR约为30 dB和40 dB时的时域恒定束宽波束输出处理结果如图12所示。

图12中黑框为截取的动目标回波信号，图12(a)中干信比30 dB时，多普勒频偏估计为29.5 Hz，图12(b)中干信比40 dB时，多普勒频偏估计为34 Hz。可以看出，利用图10的时域恒定束宽波束图对目标回波进行接收，在较精确恢复回波信号的同时，抑制了固定方向的相干干扰，正确估计出动目标的多普勒频偏。

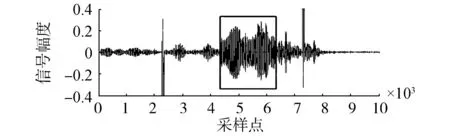
(a)ISR=30 dB

(b)ISR=40 dB图12 波束输出信号Fig.12 The beam output signal

5 结论

本文给出了一种基于相干干扰抑制的恒定束宽时域实现方法。该方法在相同的滤波器阶数下提高了旁瓣和零陷的设计精度，并通过计算机仿真和水池试验验证了该方法在对波束主瓣内偏离主轴方向的弱信号恢复的同时，实现了固定方向的干扰抑制，正确估计出动目标的多普勒频偏。

[1]鄢社锋, 马远良. 基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成[J]. 声学学报, 2005, 30(4): 309-316. YAN Shefeng, MA Yuanliang. Broadband constant beamwidth beamforming for arbitrary sensor arrays in time domain via second-order cone programming[J]. Acta acustica, 2005, 30(4): 309-316.

[2]GODARA L C. Application of the fast Fourier transform to broadband beamforming[J]. The journal of the acoustical society of America, 1995, 98(1): 230-240.

[3]鄢社锋, 马晓川. 宽带波束形成器的设计与实现[J]. 声学学报, 2008, 33(4): 316-326. YAN Shefeng, MA Xiaochuan. Designs and implementations of broadband beamformers[J]. Acta acustica, 2008, 33(4): 316-326.

[4]姚直象, 惠俊英, 蔡志明. 矢量阵强相干干扰抑制技术研究[J]. 华中科技大学学报: 自然科学版, 2008, 36(3): 69-72. YAO Zhixiang, HUI Junying, CAI Zhiming. Suppressing strong coherent interference by acoustical vector sensor array[J]. Journal of Huazhong university of science and technology: natural science edition, 2008, 36(3): 69-72.

[5]吴海洲, 陶然, 单涛. 基于DTTB照射源的无源雷达直达波干扰抑制[J]. 电子与信息学报, 2009, 31(9): 2033-2038.

WU Haizhou, TAO Ran, SHAN Tao. Direct-path interference suppression for passive radar based on DTTB illuminator[J]. Journal of electronics & information technology, 2009, 31(9): 2033-2038.

[6]肖红侠, 项建弘. 基于调零技术的相干干扰抑制方法[J]. 计算机应用研究, 2013, 30(6): 1779-1782. XIAO Hongxia, XIANG Jianhong. Coherent interference suppression method for nulling technology[J]. Application research of computers, 2013, 30(6): 1779-1782.

[7]姚瑶, 张明敏, 袁骏. 基于零陷展宽的双基地声纳直达波抑制算法[J]. 声学技术, 2012, 31(3): 310-313. YAO Yao, ZHANG Mingmin, YUAN Jun. A direct path interference suppression algorithm of bistatic sonar based on null broaden method[J]. Technical acoustics, 2012, 31(3): 310-313.

[8]黄聪, 孙大军, 张殿伦, 等. 强相干干扰下基于二阶锥规划的圆弧阵宽带二维成像[J]. 电子与信息学报, 2014, 36(11): 2633-2639. HUANG Cong, SUN Dajun, ZHANG Dianlun, et al. Wideband two-dimensional imaging with arc array based on second-order cone programming under strong coherent interference[J]. Journal of electronics & information technology, 2014, 36(11): 2633-2639.

[9]张潇. 基于凸优化的稳健接收波束形成[D]. 成都: 电子科技大学, 2011: 6-20. ZHANG Xiao. Robust receive beamforming based on convex optimization[D]. Chengdu: University of Electronic Science and Technology of China, 2011: 6-20.

[10]苏明花. 凸优化及相关问题的研究[D]. 成都: 四川师范大学, 2008: 5-12. SU Minghua. Research on convex optimization problems and related problems[D]. Chengdu: Sichuan Normal University, 2008: 5-12.

[11]顾剑. 非凸二阶锥规划问题的非线性重新尺度化方法[D]. 大连: 大连理工大学, 2009: 2-15. GU Jian. Nonlinear rescaling methods for solving nonconvex second-order cone programming problems[D]. Dalian: Dalian University of Technology, 2009: 2-15.

[12]范展, 梁国龙. 基于凸优化的最小旁瓣恒定束宽时域宽带波束形成[J]. 电子学报, 2013, 41(5): 943-948. FANG Zhan, LIANG Guolong. Broadband beamforming with minimum sidelobe and constant beamwidth based on convex optimization[J]. Acta electronica sinica, 2013, 41(5): 943-948.

[13]马海涛, 彭东立, 王华亮, 等. 宽带多普勒技术中模糊速度处理方法改进[J]. 声学学报, 2011, 36(2): 226-230. MA Haitao, PENG Dongli, WANG Hualiang, et al. An improvememt method to the ambiguous velocity in broad-band Doppler technique[J]. Acta acustica, 2011, 36(2): 226-230.

Constant beamwidth beamforming in the time domain based on coherent interference suppression

HUANG Cong1, LI Di2

(1.China Ship Development and Design Center, Wuhan 430064, China; 2. Wuchuan Shipbuliding Industry Co.,Ltd，Wuhan 430069,China)

By designing a beam null in the direction of coherent interference, constant beamwidth beamforming in the time domain, based on coherent interference suppression, achieves both a high-precision wideband signal and coherent interference in a fixed direction in the time domain. The two-step method of beamforming in the time domain is divided between beam optimization weight design and finite impulse response (FIR) filter coefficients design. Because obtain global optimization cannot be obtained by the two-step method, the performance of the side lobe and beam null degrades. To address these defects, in this paper, we propose an improved algorithm based on a global design. We design both the beam optimization weight and the FIR filter coefficients using a unified solution in the algorithm, thus improving the design precision of beamforming in the time domain. The proposed method improves weak signal detection and parameter estimation. We verify the validity of our proposed method in computer simulations and tank experiments.

constant beamwidth; coherent interference suppression; beamforming; FIR filter; second-order cone programming; array signal progressing

2016-04-19.

时间：2016-12-21.

国家重点实验室基金项目(9140C200406110C2001);国防基础科研计划(B2420132004).

黄聪(1988-), 男, 工程师, 博士.

黄聪，E-mail:huangcong@hrbeu.edu.cn.

10.11990/jheu.201604059

TN911

A

1006-7043(2017)01-0025-06

黄聪, 李迪. 基于相干干扰抑制的时域恒定束宽波束形成[J]. 哈尔滨工程大学学报， 2017, 38(1): 25-30. HUANG Cong, LI Di.Constant beamwidth beamforming in time domain based on coherent interference suppression[J]. Journal of Harbin Engineering University, 2017, 38(1): 25-30.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161221.1524.008.html