考虑迟滞特性的多级刚度扭转减振器建模及试验验证

吴虎威， 吴光强,2， 陈 祥,， 庄 婷， 朱德财

(1. 同济大学 汽车学院，上海 201804； 2. 东京大学 生产技术研究所，东京 153-8505；3. 上海萨克斯动力总成部件系统有限公司，上海 201708)

考虑迟滞特性的多级刚度扭转减振器建模及试验验证

吴虎威1， 吴光强1,2， 陈 祥1,3， 庄 婷3， 朱德财3

(1. 同济大学 汽车学院，上海 201804； 2. 东京大学 生产技术研究所，东京 153-8505；3. 上海萨克斯动力总成部件系统有限公司，上海 201708)

利用双曲正切拟合函数，建立了可推广的考虑迟滞特性的多级刚度扭转减振器扭矩传递特性数学模型，并通过了试制的多级刚度扭转减振器特性台架试验验证。探讨了基于不同拟合因子的双曲正切函数在阶跃函数和分段线性函数拟合中的应用。针对具有非对称特性的两级和三级刚度扭转减振器，建立了考虑迟滞特性的扭转减振器扭矩传递特性的非连续、不可微分的数学模型，之后利用双曲正切拟合函数重新推导了建立的扭转减振器扭矩传递特性模型，并将结果推广至多级刚度扭转减振器。利用扭转减振器台架试验，验证了利用双曲正切函数拟合的可推广的多级刚度扭转减振器扭矩传递特性模型的有效性。

拟合因子；双曲正切函数；迟滞特性；多级刚度扭转减振器；台架试验

离合器扭转减振器作为车辆动力传动系统重要部件，可改变动力传动系统扭转振动特性和缓和传动系统所受到的冲击载荷等。离合器扭转减振器具有多级线性弹性刚度和迟滞特性等非线性特征，分别对应于分段线性函数和阶跃函数等不可微分、非连续的函数。当建立包含多级离合器扭转减振器的车辆动力传动系统模型时，模型中包括多种复杂的非线性特性，采用数值仿真方法求解分析车辆动力传动系统动力学特性时，往往会引起数值难以收敛和不稳定性问题，大大降低数值仿真效率和影响计算结果的准确性。因此，有必要采用合适的方法解决扭转减振器非线性因素建模带来的数值仿真问题。

KIM等[1]较早地利用多种拟合函数对典型的分段线性函数和阶跃函数进行拟合，包括双曲正切函数、反正切函数和双曲余弦函数等拟合函数，针对存在间隙非线性函数的单自由度振子系统，分析比较了采用不同拟合函数和不同拟合因子时系统的频响特性。STEINEL[2]较早地利用数值仿真和实车实验方法，通过调教离合器扭转减振器扭转刚度大小，有效地抑制了车辆传动系统扭转波动剧烈程度。PRASAD等[3]利用汽车半消声室内实车转鼓试验，通过增加原有扭转减振器迟滞扭矩的方法，达到衰减扭转减振器波动幅值的目标，降低了变速器内齿轮敲击噪声，进而降低了驾驶室内人耳处声压级。可见，扭转减振器迟滞特性对于传动系统动力学特性可产生较大的影响，迟滞特性是扭转减振器扭矩传递特性建模必须考虑的因素。对应于扭转减振器不同刚度区间，扭转减振器迟滞力矩大小不同，从而多级刚度扭转减振器数学模型包括分段线性函数和阶跃函数。YOON等[4-6]初步推导了刚度对称的多级刚度离合器扭转减振器扭矩传递数学模型，分析了不同多级刚度扭转减振器特性对于手动变速器齿轮敲击特性影响规律，但是推导的扭转减振器扭矩传递数学模型具有一定局限性，因工程实际中采用的大多是刚度非对称、转折转角非对称的扭转减振器，并且减振器数学模型缺乏有效的试验验证。在国内，研究多集中于离合器扭转减振器台架、实车性能试验或者扭转减振器弹性特性参数调教对于车辆传动系统动力学特性影响分析[7]，如通过扭转减振器性能参数调教抑制手动变速器齿轮敲击异常噪声，然而对于考虑迟滞特性的多级刚度扭转减振器扭矩传递特性数学建模的研究很少。

综合上述的研究成果和不足，本文利用双曲正切拟合函数，推导了可推广的具有非对称特性的考虑迟滞特性的多级刚度扭转减振器扭矩传递特性数学模型，并通过试制的某款三级刚度扭转减振器样件台架试验结果，验证了经过双曲正切函数拟合的考虑迟滞特性的多级刚度扭转减振器扭矩传递特性数学模型的有效性。

1 双曲正切函数在特殊函数曲线拟合中的应用

本节探讨基于不同拟合因子的双曲正切函数在阶跃函数和分段线性函数曲线拟合中的应用，说明利用连续、可微分的函数替代非连续、不可微分函数的可行性。

双曲正切函数如式(1)所示：

(1)

对于阶跃函数，以典型的符号函数为例(如式(2)所示)，说明双曲正切函数在阶跃函数函数拟合中的应用，对应的拟合函数如式(3)所示。

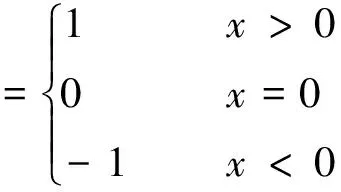
(2)

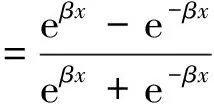
(3)

式中，β为拟合因子(Smoothing Factor, SF)。

由符号函数得到的原始值和基于不同拟合因子得到的拟合值如图1所示。可见，当拟合因子β取不同值时，对于原符号函数拟合程度不同，误差较大处发生在转折点x=0处，且β取值越大，对于阶跃函数拟合程度越好。因此，可通过合理控制β值大小，利用连续、可微分的双曲正切函数替代阶跃函数。

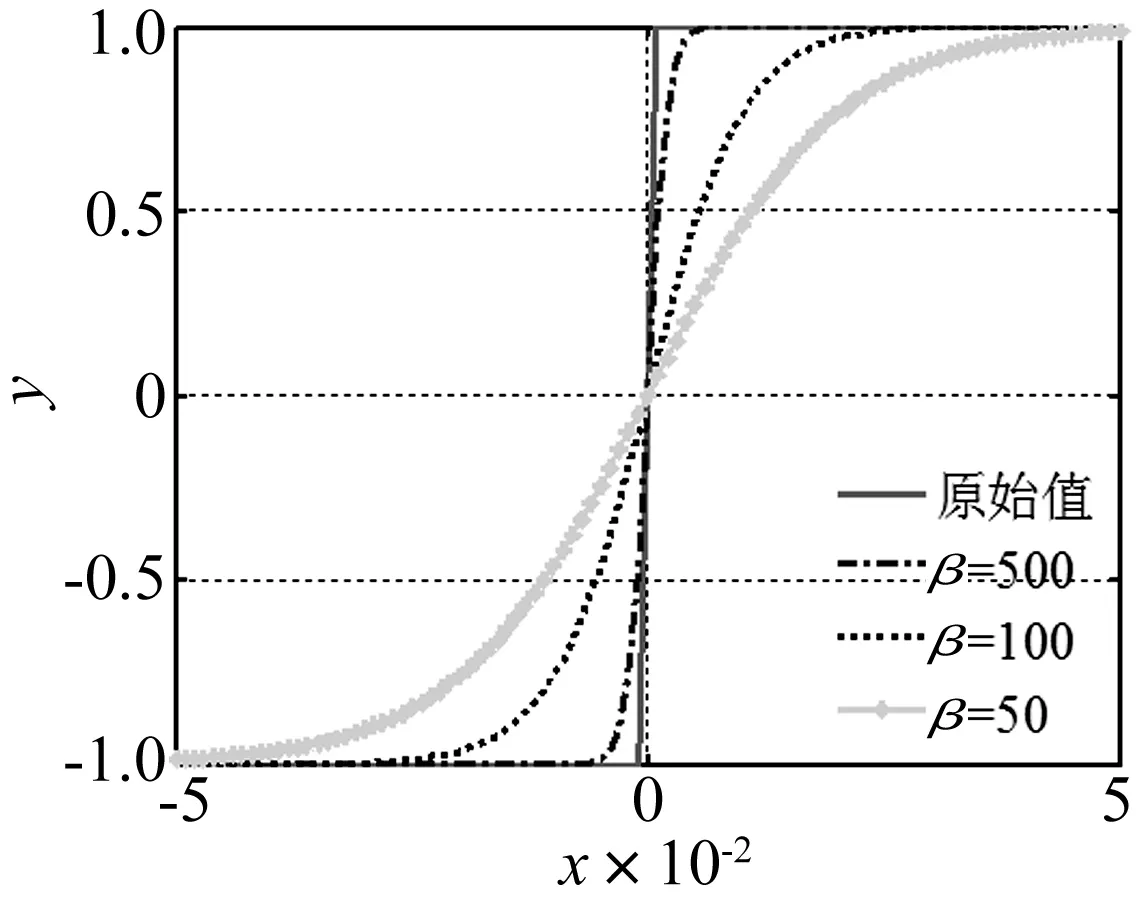
图1 双曲正切函数在阶跃函数拟合中的应用Fig.1 Hyperbolic-tangent function application on the profile fitting of the step function

对于分段线性函数，以式(4)中的分段函数为例，说明双曲正切函数在分段线性函数拟合中的应用，与式(4)对应的拟合后的函数如式(5)所示。

(4)

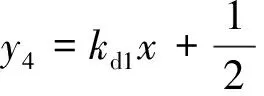
{tanh[β(x-φd1)]+1}

(5)

式中，各参数值大小分别为：kd1=0.26，kd2=13，φd1=0.05。

由分段线性函数得到的原始值和基于不同拟合因子得到的拟合值如图2所示。可知，对于分段线性函数，拟合误差最大值发生在分段函数转折点x=0.05附近，当拟合因子β取较大值时误差值越小。但是，当kd1值接近于零时，利用数值仿真时可引起数值不稳定性问题，对于仿真结果影响较大，此时拟合因子β大小的确定需综合数值仿真迭代步长的大小。

(a)整个区间的原始值和拟合值对比结果(b)0～0．05区间内原始值和拟合值对比结果(c)0．05～0．07区间内原始值和拟合值对比结果图2 双曲正切函数在分段线性函数拟合中的应用Fig．2Hyperbolic⁃tangentfunctionapplicationontheprofilefittingofthepiecewiselinearfunction

2 离合器多级刚度扭转减振器非线性特性建模

2.1 具有非对称特性的多级刚度扭转减振器特性建模

本节针对离合器工作驱动侧(Driver Side)和滑行侧(Coast Side)特性参数非对称的两级和三级刚度扭转减振器，建立扭转减振器扭矩传递特性数学模型。

对于二级刚度扭转减振器，扭矩传递特性曲线如图3(a)中所示，扭转减振器传递扭矩由弹性扭矩TS2、迟滞扭矩TH2和预加载扭矩TP2三部分组成，各扭矩特性曲线分别如图3(b)、图3(c)和图3(d)所示。此时，二级刚度扭转减振器传递扭矩大小为：

TC2=TS2+TH2+TP2

(6)

其中，弹性扭矩TS2大小为：

(7)

式中，θr为主从动摩擦盘与从动盘毂之间的相对转角；kd1和kd2分别为离合器工作驱动侧的第一级弹性刚度和第二级弹性刚度；kc2为离合器工作滑行侧的第二级弹性刚度；φd1为离合器工作驱动侧的第一级和第二级弹性刚度间的转折转角；φc1为离合器工作滑行侧的第一级和第二级弹性刚度间的转折转角。

迟滞扭矩TH2大小为：

(8)

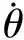
预加载扭矩TP2大小为：

(9)

式中，TPL1和TPL2为预加载力矩大小；φpl为预加载力矩作用的角度。

由式(7)～式(9)可知，对于二级刚度扭转减振器，弹性扭矩TS2为相对转角θr的分段线性函数，迟滞扭矩TH2和预加载扭矩TP2为相对转角θr的阶跃函数。

(a) 整体传递扭矩 (b) 弹性扭矩

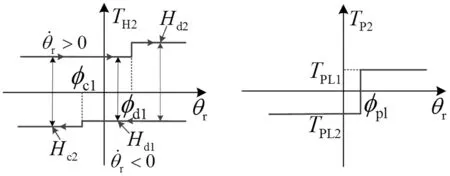
(c) 迟滞扭矩 (d) 预加载扭矩图3 具有非对称特性参数的两级刚度扭转减振器特性曲线Fig.3 Nonlinear characteristics of a two-staged stiffness clutch damper with asymmetric parameters

对于三级刚度扭转减振器，扭矩传递特性曲线如图4(a)中所示，其传递扭矩TC3大小为：

TC3=TS3+TH3+TP3

(10)

其中，弹性扭矩TS3特性曲线如图4(b)所示，扭矩大小为：

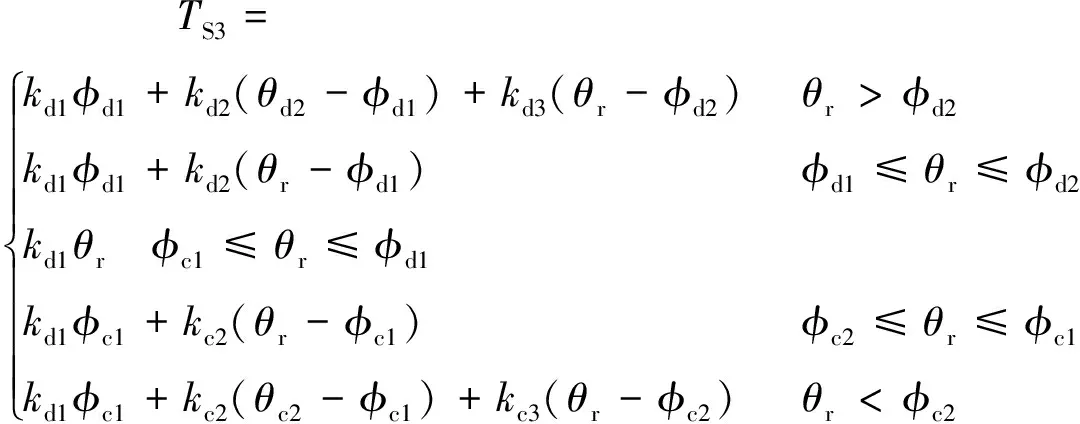
式中，kd3为离合器工作驱动侧的第三级弹性刚度；kc3为离合器工作滑行侧的第三级弹性刚度；φd2为离合器工作驱动侧的第二级和第三级弹性刚度间的转折转角；φc2为离合器工作滑行侧的第二级和第三级弹性刚度间的转折转角。

迟滞扭矩TH3特性曲线如图4(c)所示，扭矩大小为：

式中，Hd3为离合器工作驱动侧的第三级迟滞扭矩；Hc3为离合器工作滑行侧的第三级迟滞扭矩。

预加载扭矩TP3特性曲线如图4(d)所示，扭矩大小为：

(13)

(a) 整体传递扭矩 (b) 弹性扭矩

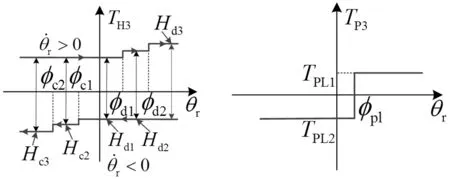
(c) 迟滞扭矩 (d) 预加载扭矩图4 具有非对称特性参数的三级刚度扭转减振器特性曲线Fig.4 Nonlinear characteristics of a three-staged stiffness clutch damper with asymmetric parameters

同样，由式(11)～式(13)可知，对于三级刚度扭转减振器，弹性扭矩TS3为相对转角θr的分段线性函数，迟滞扭矩TH3和预加载扭矩TP3为相对转角θr的阶跃函数。

2.2 基于函数拟合的离合器多级刚度扭转减振器建模

由2.1节可知，多级刚度扭转减振器传递扭矩大小为相对转角的分段线性函数和阶跃函数的叠加。如前所述，分段线性函数和阶跃函数叠加后的函数为非连续、不可微分函数，将由分段线性函数和阶跃函数叠加得到的多级刚度扭转减振器扭矩传递数学模型应用于车辆动力传动系统动力学仿真模型计算时，容易引起数值计算问题。因此，有必要利用小节1中引入的连续、可微分的双曲正切函数拟合替代分段线性函数和阶跃函数，通过调整拟合因子控制误差大小。

对于两级刚度扭转减振器，利用双曲正切函数对式(7)、式(8)和式(9)分别进行拟合，有：

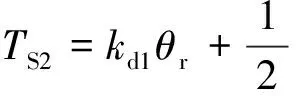
(θr-φd1){tanh[βSd1(θr-φd1)]+1}

(14)

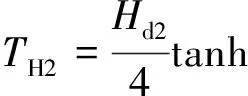
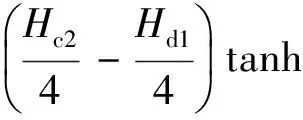
(15)

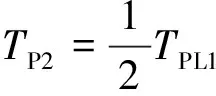
(16)

式中，βSd1为驱动侧第一级和第二级弹性刚度间的拟合因子；βSc1为滑行侧第一级和第二级弹性刚度间的拟合因子；βHd1为驱动侧第一级和第二级迟滞扭矩间的拟合因子；βHc1为滑行侧第一级和第二级迟滞扭矩间的拟合因子；βpl为预加载扭矩的拟合因子。

对于三级刚度扭转减振器，利用双曲正切函数对式(11)、式(12)和式(13)分别进行拟合，有：

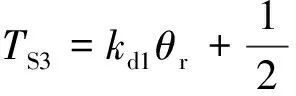
(θr-φd1){tanh[βSd1(θr-φd1)]+1}+

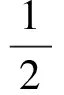
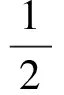
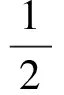
(17)

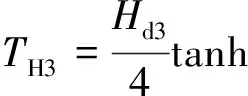
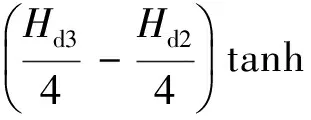
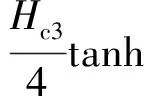
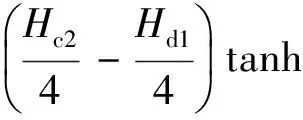
(18)

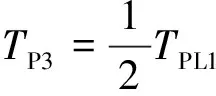
(19)

式中，βSd2为驱动侧第二级和第三级弹性刚度间的拟合因子；βSc2为滑行侧第二级和第三级弹性刚度间的拟合因子；βHd2为驱动侧第二级和第三级迟滞扭矩间的拟合因子；βHc2为滑行侧第二级和第三级迟滞扭矩间的拟合因子。

2.3 基于拟合函数的多级刚度离合器扭转减振器建模的推广

基于2.2节中的双曲正切函数拟合的两级刚度和三级刚度扭转减振器传递扭矩数学模型，将结果拓展至多级刚度扭转减振器扭矩传递特性模型。分别定义kd1=kc1和Hd1=Hc1，则对于多级刚度扭转减振器，有：

TCN=TSN+THN+TPLN

(20)

{tanh[βHd i-1(θr-φdi-1)]+1}-

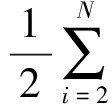
(θr-φci-1){tanh[βHci-1(θr-φci-1)]-1}

(21)

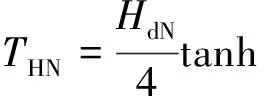
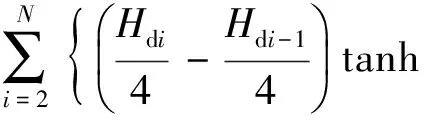
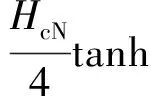
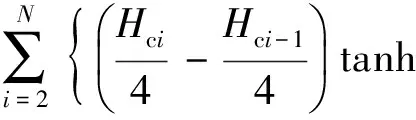
(22)

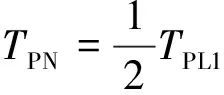
(23)

式中，N为离合器扭转减振器驱动侧或滑行侧的工作级数；kdi为扭转减振器工作驱动侧的第i级弹性刚度；φdi-1为驱动侧的第i-1级弹性刚度和第i级弹性刚度间的转折转角；kci为扭转减振器工作滑行侧的第i级弹性刚度；φci-1为扭转减振器工作滑行侧的第i-1级弹性刚度和第i级弹性刚度间的转折转角；Hdi为扭转减振器工作驱动侧的第i级迟滞扭矩；Hci为扭转减振器工作滑行侧的第i级迟滞扭矩；βHdi-1为驱动侧第i-1级和第i级弹性刚度间的拟合因子；βHci-1为滑行侧第i-1级和第i级弹性刚度间的拟合因子；βSci-1为驱动侧第i-1级和第i级迟滞扭矩间的拟合因子；βSci-1为滑行侧第i-1级和第i级迟滞扭矩间的拟合因子。

3 多级刚度扭转减振器设计及模型的试验验证

3.1 多级刚度扭转减振器参数设计及试验验证

以典型的具有非对称特性的三级刚度扭转减振器为例，来验证由双曲正切函数拟合后的多级刚度扭转减振器扭矩传递特性数学模型的有效性,该款三级刚度扭转减振器扭矩传递特性参数前期设计值如表1中所示。

根据表1中所列设计参数值，进行了该款三级刚度扭转减振器样件试制，并利用图5中的离合器扭转减振器扭矩传递特性台架试验验证。试验过程如下：首先，将从动盘样件置于测试台架的芯棒上，台架上压盘下行压住摩擦片，芯棒以较低的旋转速度预旋转一个来回，确定从动盘刚度零点位置和正向反向的极限角度。其次，芯棒回到刚度零点位置，加载扭矩使芯棒以较低的速度正向旋转至极限转角，之后卸载扭矩至芯棒回到零点位置，同时将扭矩传感器测得的扭矩数据保存于系统中，反向旋转亦然。最后，将正向和反向所测扭矩数据导出。此时，得到该款具有非对称特性参数的三级扭转减振器扭矩传递特性曲线如图6所示。为了验证试制样件的可靠性，测量了该款扭转减振器部分特性参数，各测量位置如图6中“★”处所示，测得的各参数值如表1中所列测试值。由表1中的设计值与测试值大小对比可知，该试制样件的特性参数值与原始设计值基本保持一致，误差均在工程允许范围内，样件试制可靠。

表1 具有非对称特性的三级刚度扭转减振器特性参数列表

图5 离合器三级刚度扭转减振器特性台架试验Fig.5 Bench testing of the three-staged stiffness clutch damper characteristics

图6 具有非对称参数的三级刚度扭转减振器特性台架测试结果Fig.6 Bench testing results of the three-staged stiffness clutch damper characteristics with asymmetric parameters

3.2 基于双曲正切函数拟合的扭转减振器模型的试验验证

为了探讨由双曲正切函数拟合后的多级刚度扭转减振器扭矩传递特性数学模型的有效性，针对如图6所示的三级刚度扭转减振器扭矩传递特性曲线，利用式(20)～式(23)，选取的一组合适的拟合因子参数如表2所示，可见各拟合因子大小不同，此时得到该三级刚度扭转减振器扭矩传递特性曲线如图7所示。

表2 拟合因子参数列表

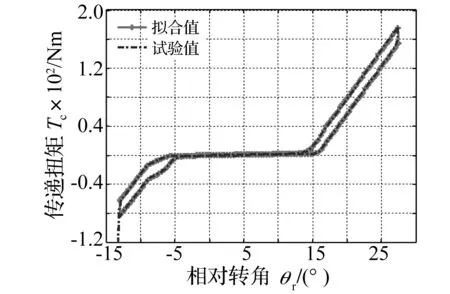
图7 离合器扭转减振器特性拟合值与试验值对比Fig.7 Comparisons between the fitted and experimental value of the multi-staged clutch damper characteristics

由图7中拟合值和试验值对比可知，利用双曲正切函数拟合的扭矩传递特性数学模型得到的拟合值与试制样件台架试验的试验值基本保持一致。将转折转角处扭矩传递特性曲线局部放大后结果如图8和9所示，转折转角附近拟合值与台架试验的测试值基本保持一致，误差值均小于5%，属于工程允许范围，因此可证明利用双曲正切函数拟合的扭矩传递特性数学模型得到的拟合值可靠，该模型可进一步用于包括该三级刚度扭转减振器模型的数值仿真中。

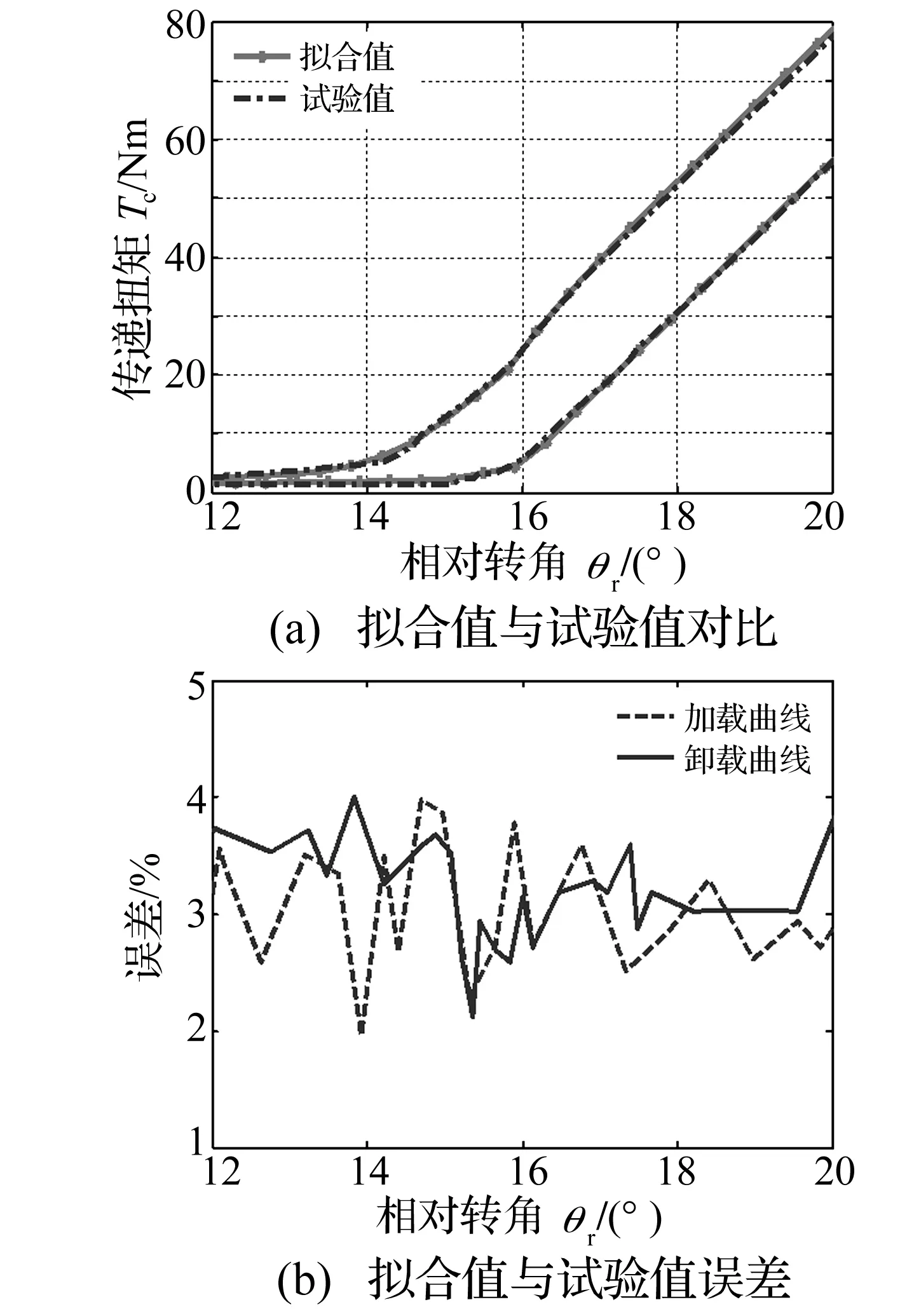
图8 特性曲线拟合值与试验值对比局部放大结果Fig.8 Partial enlarged view of comparisons between the fitted and experimental value

图9 特性曲线拟合值与试验值对比局部放大结果Fig.9 Partial enlarged view of comparisons between the fitted and experimental value

鉴于可推广的多级刚度扭转减振器扭矩传递特性数学模型是利用二级、三级刚度扭转减振器扭矩传递特性数学模型类推得到，可涵盖所有级数刚度的扭转减振器，此处利用试验验证了由可推广的多级刚度扭转减振器扭矩传递特性数学模型得到的三级刚度扭转减振器扭矩传递特性的准确性，因此验证了利用双曲正切函数拟合的多级刚度扭转减振器扭矩传递特性方法的有效性。

4 结 论

为了解决带有阶跃函数和分段线性函数特性的多级刚度离合器扭转减振器模型的数值仿真存在的数值收敛性和稳定性问题，文中利用连续、可微分的双曲正切拟合函数，建立了考虑迟滞特性的可推广的多级刚度扭转减振器扭矩传递特性数学模型。根据离合器扭转减振器前期设计特性参数，试制了某款具有非对称特性的三级刚度扭转减振器样件，并进行了扭矩传递特性台架试验验证。结果表明，由双曲正切函数拟合后的多级刚度扭转减振器数学模型得到的扭矩传递特性曲线与台架试验测试曲线保持一致，该数学模型可进一步用于包括离合器多级刚度扭转减振器的车辆传动系统动力学分析的数值仿真，从而有效解决数值仿真存在的问题。

[1] KIM T C, ROOK T E, SINGH R. Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity[J]. Journal of Sound and Vibration, 2003, 263(3): 665-678.

[2] STEINEL K. Clutch tuning to optimize noise and vibration behavior in trucks and buses[C]//SAE 2000 International Mobility Technology Conference and Exhibition. SAE,2000.

[3] PRASAD J S, DAMODAR N C, NAIDU T S. Clutch hysteresis maximization for elimination of gear rattle in a passenger bus[C] //SAE 2013 Symposium on International Automotive Technology.SAE,2013.

[4] YOON J Y, SINGH R. Effect of the multi-staged clutch damper characteristics on the transmission gear rattle under two engine conditions[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013, 227(9): 1273-1294.

[5] YOON J Y, YOON H S. Nonlinear frequency response analysis of a multistage clutch damper with multiple nonlinearities[J]. Journal of Computational and Nonlinear Dynamics, 2014, 9(3): 031007.

[6] 徐旭初, 方伟荣, 葛凤龙, 等. 一种新型三级刚度离合器扭转减振器的开发及应用[J]. 汽车工程, 2013, 35(11): 1011-1014. XU Xuchu, FANG Weirong, GE Fenglong, et al. The development and application of a novel clutch torsional damper with three-stage stiffness[J].Automotive Engineering, 2013, 35(11): 1011-1014.

[7] 刘显臣. 汽车NVH综合技术[M]. 北京：机械工业出版社, 2014.

Numerical and experimental analysis on multi-staged stiffness clutch dampers considering hysteresis characteristics

WU Huwei1, WU Guangqiang1,2, CHEN Xiang1,3, ZHUANG Ting3, ZHU Decai3

(1. School of Automotive Studies, Tongji University, Shanghai 201804, China；2. Institute of Industrial Science, University of Tokyo, Tokyo 153-8505, Japan;3. Shanghai Sachs Powertrain Components Systems Co., Ltd., Shanghai 201708, China)

An extensible mathmatical model for the torque transmission property of multi-staged stiffness clutch dampers considering hysteresis characteristics was established in virtue of the hyperbolic-tangent fitting function, which was then validated by the bench tests of a certain prototype. The hyperbolic-tangent functions with different smoothing factors were applied to the profile fitting of step function and piecewise linear function. Then, a discontinuous and non-differential numerical model for the two-staged and three-staged stiffness clutch dampers with asymmetric characteristics, taking into account the hysteresis characteristics, was derived. The numerical model was further modified by using the hyperbolic-tangent function and extended to multi-staged stiffness clutch dampers. Finally, the modified model for the multi-staged stiffness clutch dampers fitting was validated by bench tests of the prototype.

smoothing factor; hyperbolic-tangent function; hysteresis characteristics; multi-staged stiffness clutch damper; bench test

国家自然科学基金(51175379;51575393)

2015-10-27 修改稿收到日期：2015-12-11

吴虎威 男，博士生，1987年生

吴光强 男，教授，博士生导师，1965年生

U463.21

A

10.13465/j.cnki.jvs.2017.02.028