单层球面网壳动力失效全过程试验研究

巴盼锋， 张毅刚， 吴金志， 张致豪， 郑修娟

(北京工业大学 空间结构研究中心，北京 100124)

单层球面网壳动力失效全过程试验研究

巴盼锋， 张毅刚， 吴金志， 张致豪， 郑修娟

(北京工业大学 空间结构研究中心，北京 100124)

为了更加深入研究单层球面网壳的动力失效。结合一个K6型单层球面网壳振动台试验，设计出一套描述单层球面网壳强振倒塌全过程的测试方法，包括：冲击法测试结构自振特性、低频调幅加载评估损伤程度和基频简谐加载监测结构失效过程。结合数据测量结果，描绘出结构倒塌过程的变形时程，分析结构的基频、阻尼及振型，记录杆件进入塑性的顺序，探索结构损伤演化的规律及倒塌破坏的机理。最后考虑材料的损伤，进行有限元模拟，验证了模拟方法的正确性。

振动台试验；变形时程；自振特性；损伤评估；失效全过程

我国近些年空间结构的飞速发展，让人们更加深刻认识的单层球面网壳结构轻质、优美的特征。但对于一个处于地震频发带上的中国，地震的频发给人们带来了极大的灾难，人们在灾难面前更加清醒的认识到，如何更清楚的掌握单层球面网壳强震破坏机理显得更有必要。所以针对这一问题，各国学者都进行了大量理论研究，主要的研究集中在用计算机去模拟整体结构的强震破坏过程[1-7]。但是如何能够采用试验室现有的手段去测量单层球面网壳强震下的倒塌全过程，这也是现有试验的难点所在。

国内外针对单层球面网壳的振动台倒塌试验做了很多，试验目的各不相同。范峰等[8]通过对一单层球面网壳的振动台试验，根据倒塌现象对单层球壳结构的强度破坏和稳定性破坏加以验证。王秀丽等[9]通过振动台试验研究一种网格结构杆件阻尼器，考虑阻尼作用对单层网壳的减震效果。叶继红等[10]对三个单层球面网壳进行振动台试验，通过设置薄弱区域，验证极限承载力破坏和强度破坏与计算机模拟的一致性。由于振动台试验中网壳倒塌发生突然，上述研究只能观察到破坏的最终现象，失效全过程难以监测并记录，给网壳失效机理的验证带来困难。为解决这一难题，本文认真研究了现有试验数据采集设备，设计出一套包括自振特性、损伤程度评估和失效过程的测试方法，试图描述出单层球面网壳强振倒塌的全过程。最后考虑材料的损伤，计算机模拟整体结构破坏的过程，对比分析试验数据和模拟结果，验证了模拟方法的正确性。

1 单层球面网壳试验模型

1.1 结构试验模型

K6型单层球面网壳采用Q235的热轧钢管制作，其中直径为10 mm的钢管，平均壁厚1.01 mm。为了模拟结构在有初始缺陷的情况下，整体结构破坏的薄弱位置，其中两根杆件采用直径为8 mm的钢管，布置在最外环的主肋和斜杆上，壁厚1.02 mm，见图1。结构矢跨比1/5，跨度为3 000 mm。节点采用直径为200 mm的实心球，球的质量为32.4 kg，材料采用Q450的热轧钢。

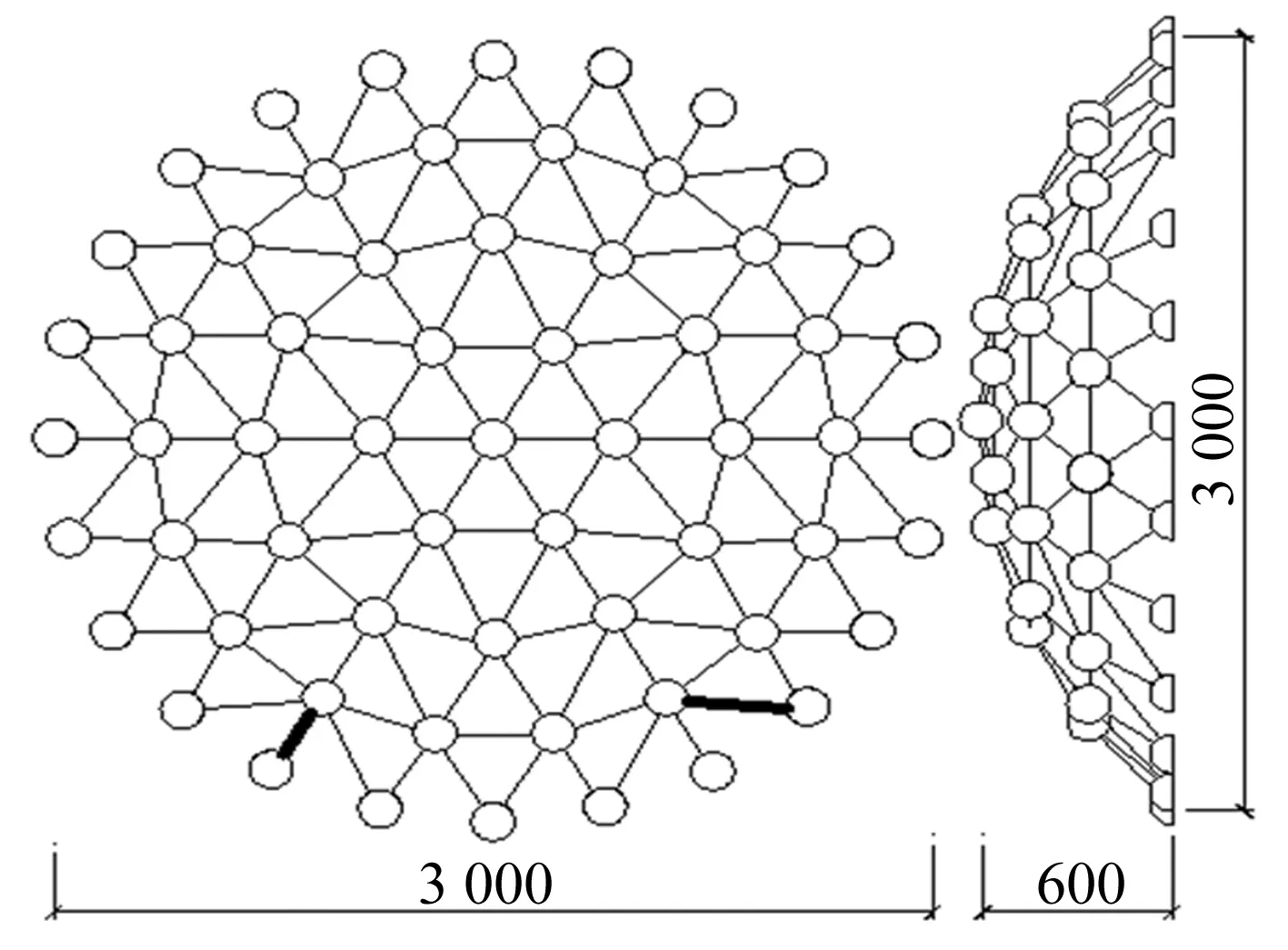
图1 网壳试验模型尺寸(mm)Fig.1 Thesize of test model(mm)

试验室现有的振动台台面尺寸为1 m×1 m，台面高度为1 m。为了放大振动台的台面，做了两根3.25 m长的箱梁做十字交叉状，箱梁中部预留螺栓孔与振动台相连。箱梁上部设置10 mm厚的钢板，钢板上设置300 mm高的钢垫块，垫块位于箱梁的端部。在垫块上部设置八边形环梁，单层球面网壳布设在八边环梁上。模型组装如图2。

图2 结构组装模型图Fig.2 The assembly model figure of the structure

1.2 钢管拉伸试验

为建立起真实的材料本构关系，对钢管取样进行拉伸试验。本次取样共计6根钢管试件。

分析图3给出应力应变关系曲线可知：该批钢管具有很好的塑性行为，钢材拉伸过程中的四个阶段明显，延性比较好，最大伸长率达0.37，最小伸长率也超过0.25。钢管在热加工过程中，管径与壁厚均会产生一定的偏差。试验所用的杆件测量结果表明，杆件的平均直径为10.070 mm，杆件的平均壁厚为1.090 mm。

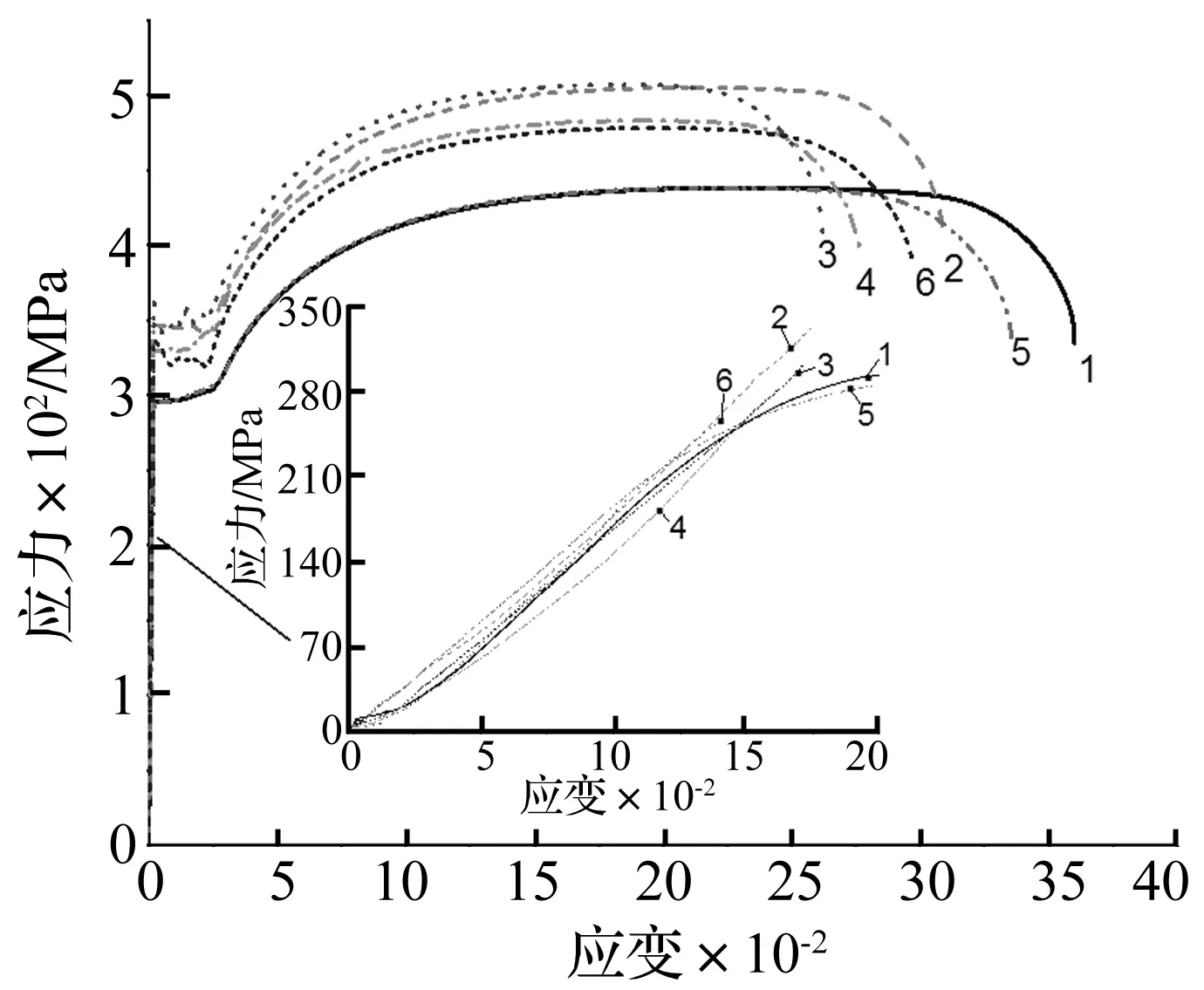
图3 应力-应变关系曲线Fig.3 The relationship curves of stress-strain

其中4号试件由于存在一定的初始弯曲，初始位移增速较大，导致弹性模量偏低(图3)。所以对于4号试件的弹性模量的测试结果予以舍去。其余试件的平均弹性模量为192.8 GPa，试件的平均屈服强度为319.8 MPa。

1.3 测点布置

对单层球面网壳的杆件应变测点布置，主要考虑结构的对称形式，对于整体结构的1/3片区进行重点监测，对其余结构贴部分应变片进行校对。结构的应变监测主要布置在主肋及环向杆件上，如图4。

图4 应变片布设图Fig.4 The figure of strain gauge

对于结构位移的测量，主要采用两台平面非接触式位移计进行测量。另外在结构上布设了12个拉线位移计进行位移校对，其中3个拉线位移计用于测量振动台的三台作动器位移，振动台相关系数见表1。其余位移计测量上部结构的位移，位移计布设如图5。

加速度传感器结合振动情况及模拟结果，主要以监测竖向加速度为主，分布位置如图8。

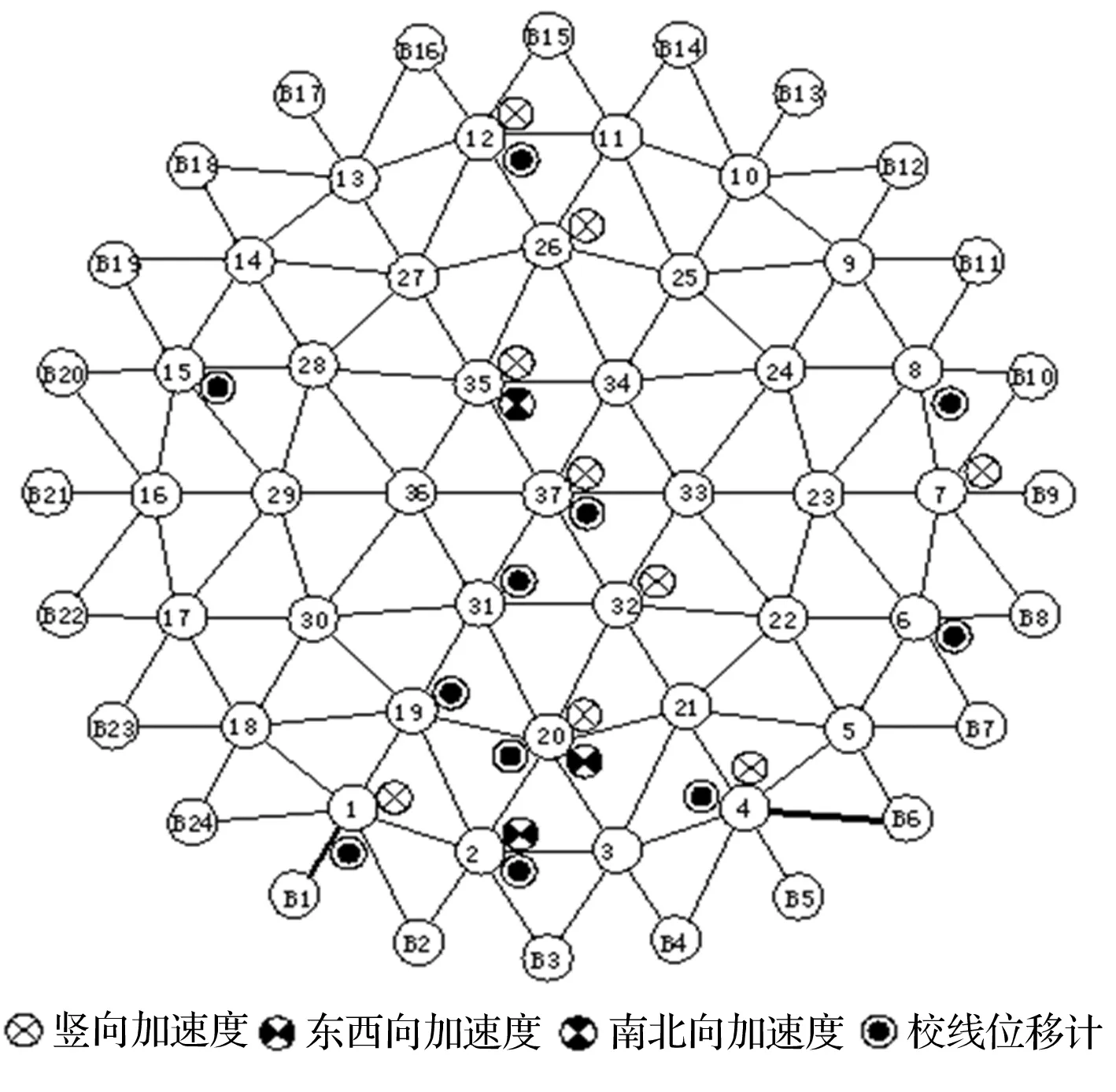
图5 加速度传感器及位移计的布设图Fig.5 The figure of acceleration sensors and displacement meter

作动器3个台面高度1m台面尺寸1m×1m控制方式位移控制振动台控制方向Z作动器行程±7.5cm频率范围0.5～50Hz峰值加速度1.5g

2 冲击法测试结构自振特性

对于结构自振特性的测试，采用冲击法进行，对被测结构不产生附加质量。由于采用作动器进行激励，所以输入能量可以得到保证，从而有效的提高信噪比。但输入的能量过大，会导致高阶频率范围降低，影响结构高阶特性测试的准确性。由于主要需要掌握前几个低阶频率，所以采用冲击法具有可行性。本次试验在北京工业大学结构试验中心进行，振动台输入正弦脉冲，保持一些测量点不变，通过变换其余加速度计的位置，进行结构所有点、所有方向的加速度测量。结合不动点进行数据归一，调整在同一激励下的测试结果，然后对网壳所有测点的振动结果进行分析，得到结构的各阶自振特性。

2.1 自振频率和阻尼比

为了更加精准的确定结构的模态，采用两种方法确定结构的自振频率。并对两种方法所得到的结果进行平均。

方法一：结合加速度传感器测得的结构振动响应数据，采用商业分析软件DASP进行数据分析，通过和东方所不同软件和硬件设备的配合，可以构成一个可进行多种动静态试验的试验室。其中每个模块下均包含多种功能，各种功能可以交错使用，在测试和分析功能上突破很多以往信号分析仪的种种限制。本文采用DASP中的随机减量法进行数据预处理，得到结构近似的衰减曲线，再结合ERA模态参数识别方法，从而确定结构的前三阶自振频率和阻尼比。

加速度传感器采集到的其中两条竖向衰减信号如图6(a),(c)，对应的频谱曲线如图6(b),(d)。识别出来的前三阶自振频率及阻尼比平均值见表2。

对测得的111个测点的分析结果进行汇总并求平均值。用方法二校对方法一的结果，对比发现：二者的差值均在5%以内，这也说明了采用DASP进行数据分析的结果是可信的。

图6 D-1、D-2加速度时程曲线及对应的FFT曲线Fig.6 The D-1、D-2 acceleration history curve and its corresponding FFT curve

方法二：首先对加速度时程曲线采用经验模态法进行分解，然后对分解后的一阶固有模态曲线进行随机减量处理[11]，从而获得自由衰减曲线。最后对衰减曲线进行Hibert变换，并进行最小二乘拟合，获得幅值的自然对数拟合曲线和相位角线性拟合曲线。从而得到结构的第一阶自振频率和阻尼比。采用同样的分析方法，得到结构的第二、第三阶自振频率和阻尼比。

表2 多测点平均得的结构前几阶自振频率

2.2 结构振型分析

采用DASP商业软件对所有实测数据进行振型分析，并结合ABAQUS有限元软件模拟结果，进行对比，如图7。

通过对比分析发现：一阶振型主要呈现整体水平振动，个别节点突出原模型，其余节点向下凹陷的特点。对比图7(a)中的两图可知，一致性很明显。二阶振型呈现整体竖向向下振动的特点，个别节点振动幅值较大；三阶振型呈现多个节点偏离原始位置，产生整体扭动。

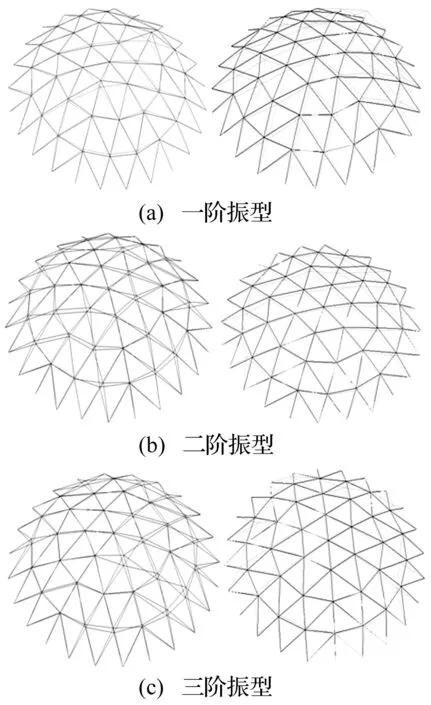
图7 结构振型实测(左)与模拟(右)结果Fig.7 The formation ofthe measured and simulated results

3 低频调幅加载评估损伤程度

结构失效前必定经过损伤累积阶段，结构的损伤累积对结构的失效过程会产生重要影响。对于杆件进入塑性形成损伤的程度，用应变片已经无法准确记录，但是杆件进入塑性的时刻还是可以通过应变片的记录获得的。通过逐步加大激励的幅值，根据杆件进入塑性的次序、数量就可以评估网壳中损伤的累积程度及发展过程。

通过钢管材性试验，已知钢管的平均屈服强度和平均弹性应变，容易计算出进入塑性的微应变为1 658 μm/m。结合振动台的最大加速度限制，且保证位移幅值在一定的范围之内可调整。故采用低频率1.66 Hz的竖向正弦波进行加载，幅值逐渐增大，振动幅值从1～30 mm，每个阶段的振动时长均为10 s。然后观察现场应变片的实测记录，跟踪杆件进入塑性的位置及顺序，见图8。

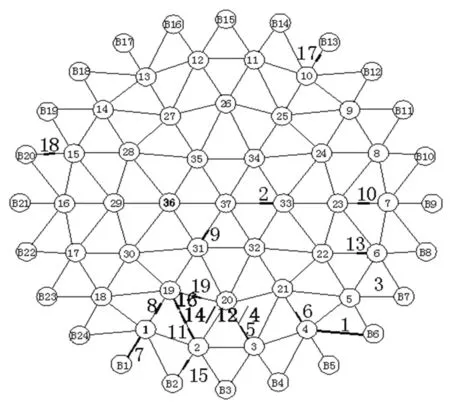
图8 杆件进入塑性的发展顺序Fig.8 The order of plastic development

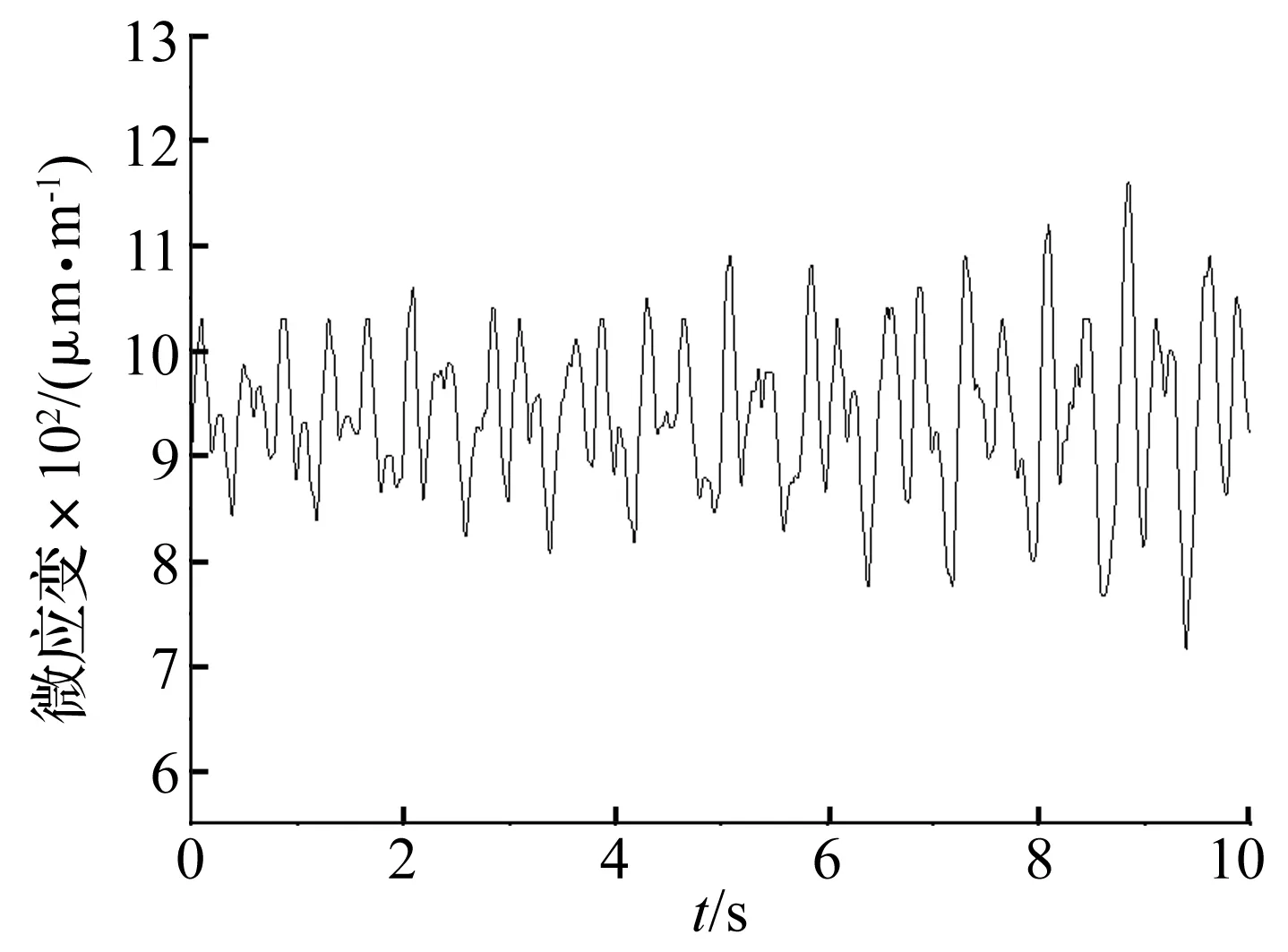
图9 Y4-1号测点微应变随加载时长的变化曲线Fig.9 The curve of the micro strain with the loading time of Y4-1

通过图8可知：最先进入塑性的应变片位于弱化杆件上，然后进入塑性杆件的比较离散，主要集中在斜杆。随着外环主肋杆件开始进入塑性(B1-1)，可以看到塑性杆件沿主肋B1-B13迅速发展并开始演化，附近区域大面积杆件陆续进入塑性，造成整体刚度降低。进一步的试验可知最先产生明显凹陷的区域中心位于35号节点(见图12(a))，注意到结构的对称性，这也应该是可以预测的。综上，该试验模型杆件塑性发展规律可归结为：塑性杆件发展先从弱化区域开始，并且在斜杆之间开始蔓延。一旦有主肋杆件进入塑性，将沿主肋迅速发展，附近区域刚度降低，产生局部凹坑，随着振动的深入，局部凹坑逐渐扩大，直至整体结构失效。

整个加载过程中，随着加载幅值的逐渐增大，微应变也逐渐增大，当幅值为18 mm时，Y4-1号测点的微应变随加载时长的变化时程曲线见图9。当幅值达到23 mm，开始有测点进入塑性，此时进入塑性的杆件为1号杆件，结合幅值从23 mm到30 mm多个阶段，测点进入塑性的数量见图10。最后结合应变片的分布区域图4，把整体结构划分为三个分区，采用对称原则，此时进入塑性的杆件比例至少为2%。采用同样的方法进行统计，在接下来的几个加载阶段，直至加载幅值为30 mm，杆件进入塑性的比例依次为4%、8%、12%、18%、24%、38%。

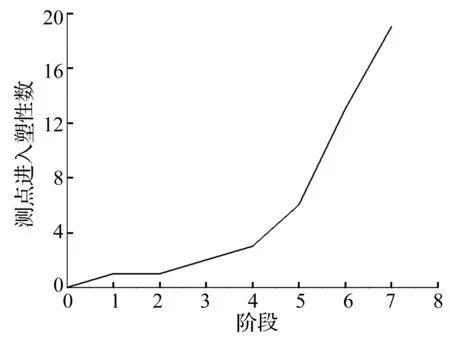
图10 不同阶段下测点进入塑性的数量Fig.10 The number of points of entry into plastic at different stages

4 基频简谐加载监测结构失效过程

4.1 非接触式位移采集设备与校正

经过相关资料的论证，发现非接触式位移采集设备具有很好的位移采集功能，它不仅可以实现上百个测点位移数据的同时采集，并且采集精度能够达到0.01 mm，足可以满足倒塌试验的要求。为了全面测量所有点位的位移信息，故本试验采用两台非接触式位移采集设备，两台非接触式位移采集设备的布设位置与结构中心点呈一条直线。

本次试验在上述发生一定损伤的网壳模型基础上进行。振动台采用位移控制系统，由于在输入位移过程中输入值和输出值有一定的差别。故采用美国Firstmark公司生产的YK12002系列拉线位移计，量程范围为±50 mm。其中两套英国IMETRUM公司生产VG5 Pro-SM-2D型非接触式位移采集设备，进行全程跟踪拍摄测量如图11。拉线位移计用于校正振动台位移输入、输出以及与非接触式拉线位移计二者之间的比例关系，通过预加载确定两台非接触式位移计与拉线位移计之间的比例系数分别为0.562、0.634，修正非接触式位移计采集系统中的比例系数，确保后续采集过程中非接触式位移计的真值。

图11 位移采集设备Fig.11 The displacement of acquisition device

4.2 加载方案

采用正弦波进行加载，主要考虑到正弦波是地震波的基本构成，任意地震波都可以采用多条不同的正弦波进行叠加而成。地震波由于规律复杂，对于整体结构失效规律的影响因素不好确定，所以采用正弦波进行加载便于规律分析。另外通过正弦波加载可以建立起结构动力响应、自振特性与荷载频谱三者之间的关系，对研究网壳失效规律更为方便。由于试验场地的限制以及固定的作动器安装方向，不可能实现非接触式位移计与水平作动器的垂直角度，对于测量的结果会带来不必要的麻烦及角度转换等误差。所以采用竖向正弦波进行加载，可以很容易的得到结构的竖向位移，避免采集所带来的角度转换等问题。

结合自振频率的分析结果，结构的一阶自振频率为16.436 Hz，阻尼比为1.25%。由于振动台控制系统为实验室开发的程序，为了提升计算速度，对于输入波形数据时间间隔进行了四舍五入，所以结合精度进行取舍，折合后的加载频率为16.1 Hz。采用自振频率进行加载，输入幅值从0.5～5 mm逐步加大，由于位移控制系统对高频输出的衰减，实际幅值输出范围为0.12～1.6 mm。每个振动幅值的加载时长从10～100 s逐渐放大，记录每个节点的位移时程，加载时长至整体结构倒塌破坏。最终输出幅值1.6 mm，时长65 s时结构发生倒塌。

4.3 全过程形态捕捉

平面非接触式位移采集设备可以采集到各个节点的位移时程。然后结合各个点的位移时程，描绘出各个时刻点整体结构的形态。

对于两套设备中数据采集的时刻点不能完全一致时，采用差分法进行拟合。一些测点被前面的杆件或者球体遮挡，非接触式位移采集设备无法准确的瞄准测点，会导致数据溢出。结合非接触式位移计采集到的视频数据，并利用软件的再次捕捉功能，在被遮挡测点附近不受影响的位置添加新的捕捉点进行再次捕捉，从视频数据中重新输出新加点的位移时程。最后结合位移时程，采用3D3S描绘出结构倒塌破坏过程。获得的几个关键形态见图12，其中左上角为根据测得的位移时程描绘的结构形态，右上角为普通摄像机摄得的视频截图，下图为非接触式位移采集设备视频数据的截图。

图12 不同时刻点，结构的形态变化图Fig.12 The morphological variation of the structure at different time points

5 试验与分析结果对比

5.1 有限元模型建立

采用ABAQUS进行数值模拟，其中模型几何信息采用现场实测值，并针对ABAQUS材料子程序进行二次开发，考虑材料的损伤[12-13]。针对节点刚域问题，对结构模型进行二次细化，用长度等于球半径的刚性单元，刚结于球圆心，去模拟球的刚性区域(图13(b))。刚性区域单元材料要远远大于杆件的材料强度，采用Reileigh阻尼，阻尼系数采用实测平均值ξ= 0.012 5。

图13 整体结构的有限元模型Fig.13 The finite element model of whole structure

5.2 试验结果与模拟值对比

第一阶频率差别较大，原因主要在材料的处理上，材料的离散性比较大，壁厚、弹性模量等系数在计算机模拟时均采用了平均值的处理方法，势必会产生一定的误差。对于节点质量产生的转动惯量没有考虑，贴脚焊缝所产生的刚域问题，也未考虑，均有可能带来以上的问题。

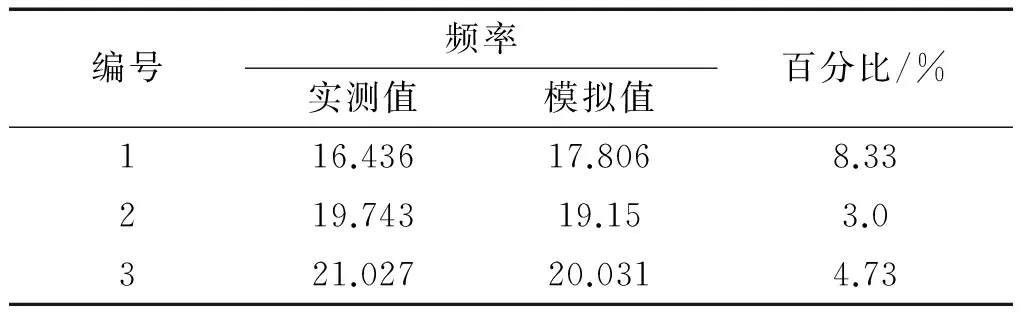
表3 自振频率模拟值与实测值对比

图14给出了网壳中心点绝对位移时程曲线，可看出试验结果与模拟结果具有很好的一致性。振动开始均沿着平衡轴跌荡前进，随着损伤的累积，中心点位移开始急剧加大，直至倒塌。整体结构模拟值与实测值的差别主要集中在由振动平衡到位移急剧增大的转折阶段，该阶段必然是损伤累积到了一定程度，开始有杆件断裂。模拟得出的断裂杆件的主要分布情况见图15(a)，可以看出断裂杆件主要是主肋和环杆，主要发生在杆件的根部单元(图15(b))。试验中观测到的断裂杆件分布与模拟有所不同，分析主要原因还是在于焊接过程中，杆件对准球心不够精确导致的，这也是图14中位移曲线转折阶段出现差别的原因。

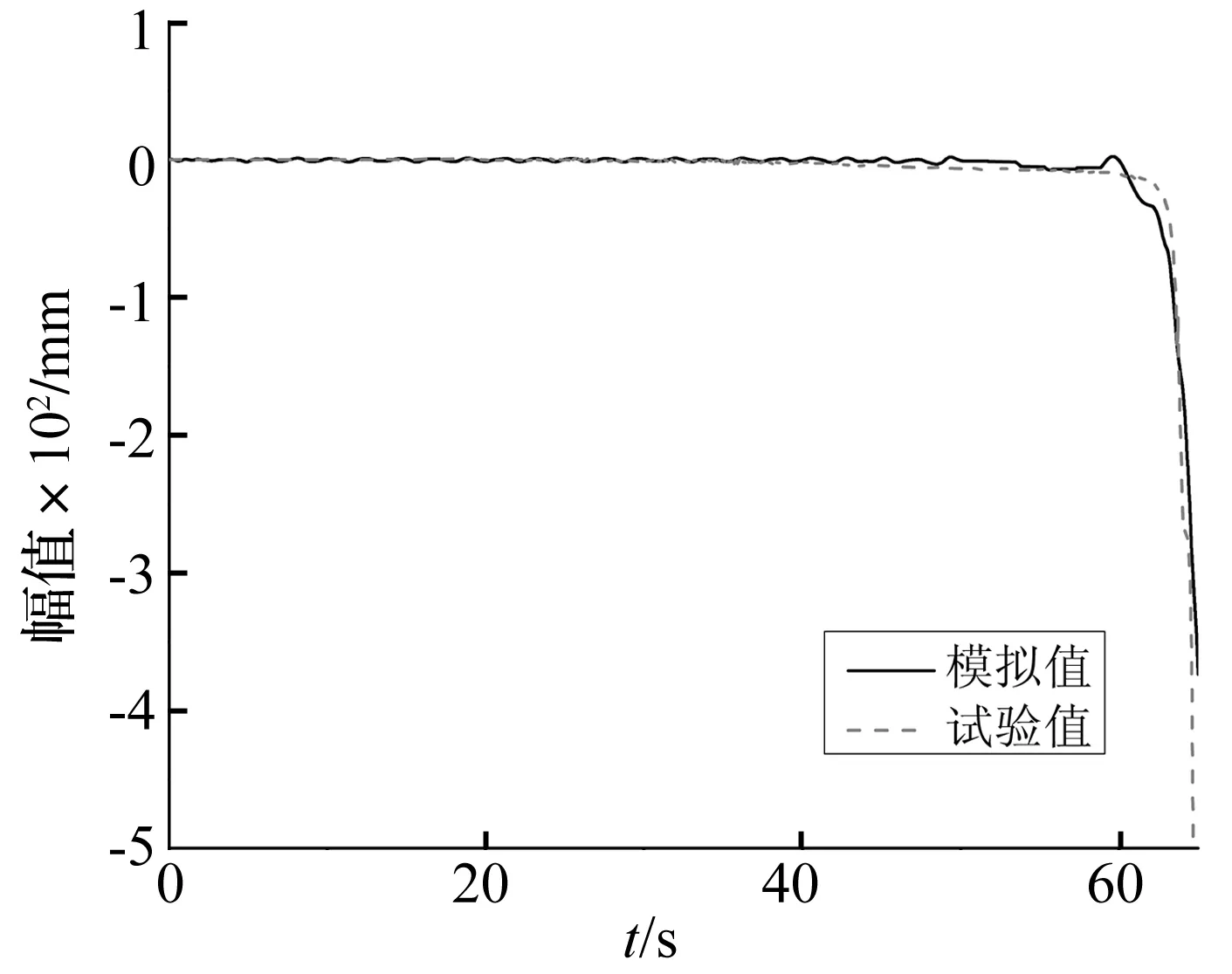
图14 网壳中心点绝对位移时程曲线Fig.14 The history curve of center point

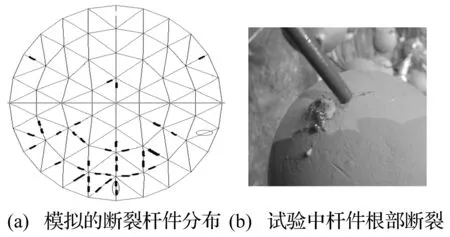
图15 断裂杆件分布图Fig.15 The distribution of failure and fracture bar

6 结 论

本文结合一个K6型单层球面网壳振动台试验，形成了描述单层球面网壳强振倒塌全过程的测试方法，得出以下主要结论：

(1)采用冲击法测试单层球壳的自振特性，可以在振动台试验过程中加以应用。前几阶低阶频率的测试结果在有效范围之内。

(2)通过低频调幅加载试验可以获得杆件进入塑性的演化发展规律，为评估振动过程中结构的损伤累积程度提供了条件。

(3)通过基频简谐加载监测单层球面网壳的失效全过程，可以描绘出结构在倒塌破坏过程中的全过程形态变化，为进一步研究结构失效规律提供了基础。

(4)通过试验结果与模拟结果对比可知，精细的有限元建模可以模拟出单层球面网壳动力失效的过程，二者在失效趋势上具有很好的一致性。

(5)网壳在动力作用下的强震失效试验证明：在结构失效之前，伴随着大量杆件进入塑性；网壳失效先从局部凹陷开始，并进一步蔓延直至整体结构失效。

[ 1 ] HIYAMA Y, TAKASHIMA H,LIJIMA T,et al. Buckling behavior of aluminum ball jointed single layered reticular domes [J].International Journal of Space Structures,2000,15(2):81-94.

[ 2 ] 沈世钊,支旭东. 球面网壳结构在强震下的失效机理[J]. 土木工程学报,2005(1):11-20. SHEN Shizhao,ZHI Xudong. Failure mechanism of reticular shells subjected to dynamic actions[J].China Civil Engineering Journal,2005(1):11-20.

[ 3 ] 聂桂波.网壳结构构件空间滞回性能试验与精细化本构模型研究[D].哈尔滨:哈尔滨工业大学,2008.

[ 4 ] 杜文风,高博青,董石麟. 单层球面网壳结构动力强度破坏的双控准则[J]. 浙江大学学报(工学版),2007,11:1916-1920. DU Wenfeng, GAO Boqing, DONG Shilin. Double-control criterion of dynamical strength failure for single layer latticed shells[J].Journal of Zhejiang University(Engineering Science),2007,11:1916-1920.

[ 5 ] 张其林,Udo Peil. 任意激励下弹性结构的稳定分析[J].土木工程学报,1998,31(1):26-32. ZHANG Qilin,Udo Peil. Stability analysis of elastics structures under arbitraryexcitation [J].China Civil Engineering Journal,1998,31(1):26-32.

[ 6 ] 聂桂波,范峰,支旭东,等.单层球面网壳结构失效机理振动台试验[J]. 土木工程学报,2013,46(10): 17-25. NIE Guibo,FAN Feng,ZHI Xudong,et al. Shaking table test on failure mechanism of single-layer reticulated dome [J]. China Civil Engineering Journal,2013,46(10):17-25.

[ 7 ] 李忠学,沈祖炎,邓长根,等. 钢网壳模型的动力稳定性振动台试验研究[J]. 实验力学,1999,14(4):484-491. LI Zhongxue,SHEN Zuyan,DENG Changgen,et al. Research on the dynamic stability of steel reticulated shells via shaking table test[J].Journal of Experimental Mechanics,1999,14(4):484-491.

[ 8 ] 范峰,支旭东,沈世钊.网壳结构强震失效机理[M].北京：科学出版社,2014:79-104.

[ 9 ] 王秀丽,马晓彤.BRB在受损单层网壳结构抗震加固中的应用于研究[J].工程抗震与加造,2013,35(6):111-117. WANG Xiuliu,MA Xiaotong.Application and research of BRB in seismic strengthening of damage single layer reticulated shells[J].Earthquake Resistant Engineering and Retrofitting,2013,35(6):111-117.

[10] 叶继红,潘锐.单层球壳模型结构振动台试验研究[J].建筑结构学报,2013,34(4):81-90. YE Jihong,PAN Rui. Shaking table test on collapse process of single-layer spherical shells[J].Journal of Building Structures,2013,34(4):81-90.

[11] 聂桂波,范峰,支旭东,等.单层球面网壳模型动力特性测试实验[J].振动与冲击,2013,32(22):200-204. NIE Guibo,FAN Feng,ZHI Xudong,et al.Dynamic characteristics test of a single-layer reticulated dome model[J]. Journal of Vibration and Shock, 2013,32(22):200-204.[12] 巴盼锋,张毅刚,吴金志.基于单元纤维的空间杆件损伤演化计算[C]//杜修力.2013年全国土木工程研究生学术论坛论文集.北京：北京工业大学出版社,2013:298-302.

[13] 张毅刚,巴盼锋,吴金志,等.基于失效的单层球面网壳损伤演化及承载力分析[J].天津大学学报(自然科学与工程技术版),2014,47(增刊7)74-78. ZHANG Yigang,BA Panfeng,WU Jinzhi,et al.Damage evolution and bearing capacity analysis of single layer spherical shell based on aging[J].Journal of Tianjin University(Science and Technology),2014,47(Sup7)74-78.

Whole process test and dynamic failure analysis for single-layer spherical lattice shells

BA Panfeng, ZHANG Yigang, WU Jinzhi, ZHANG Zhihao, ZHENG Xiujuan

(Spatial Structures Research Center, Beijing University of Technology, Beijing 100124, China)

In order to study deeply the dynamic failure process of single-layer spherical lattice shells, combining with shaking table tests of a K6 type single-layer spherical lattice shell, a set of vibration test methods describing the whole collapses process of single-layer spherical shells under strong earthquakes was designed. It included the impact method measuring natural vibration characteristics of structures, the low frequency amplitude-modulation loading assessing structural damage level, and the fundamental frequency simple harmonic loading monitoring structural failure process. Based on the data results of measurement, the collapse process’s deformation history of a structure was described. The fundamental frequency, damping and modal shapes of a structure were analyzed. The order of bars of a structure to enter a plastic state was recorded. The rules of structural damage evolution and collapse failure mechanism were explored. At last, considering material damage, the whole failure process of signle-layer spherical lattice shells was simulated with the FE method. Comparing with the test results, the correctness of the simulation method was verified.

shaking table test; deformation history; natural vibration characteristics; damage assessment; whole failure process

国家自然科学基金重大研究计划-集成项目(91315301);国家自然科学基金项目(51178009)

2015-07-17 修改稿收到日期：2015-12-01

巴盼锋 男，博士生，1984年生

张毅刚 男，硕士，教授，1949年生 E-mail: zyg@bjut.edu.cn

TU317

A

10.13465/j.cnki.jvs.2017.01.005