新型装配式竖向电涡流TMD试验研究

汪志昊， 张 闯， 周佳贞， 徐宙元

(华北水利水电大学 土木与交通学院, 郑州 450045)

新型装配式竖向电涡流TMD试验研究

汪志昊， 张 闯， 周佳贞， 徐宙元

(华北水利水电大学 土木与交通学院, 郑州 450045)

针对城市大跨度钢结构人行天桥的减振需求，研制了一种结构紧凑、装配简单的新型装配式竖向永磁式电涡流TMD样机，综合TMD样机阻尼参数测试与电涡流阻尼磁场有限元分析结果提出了电涡流阻尼的初步设计方法与磁路优化布置。结果表明：新型TMD具有优良的阻尼特性、耐久性，且易于装配，工程应用可行性强。研究得到了用于竖向TMD的电涡流阻尼磁路优选构造：导体铜板两侧的矩形永磁铁宜采用同侧极性相同、不同侧极性相反的布置方式；永磁铁宜以水平单排布置为主，间距控制在永磁铁边长的一半以内；永磁铁必须安装2排或多排时，上下2排间距不宜小于永磁铁边长。

人行天桥；振动控制；调谐质量阻尼器；电涡流阻尼；磁路优化

随着城市化进程与立体化交通的发展，国内大跨径人行天桥的建设越来越多，单跨40 m的简支人行天桥往往难以满足中国《城市人行天桥与人行地道技术规范》(CJJ 69—95)不宜小于3 Hz的规定。为方便施工，城市过街天桥多采用简支钢箱梁结构。固有阻尼极低的简支钢箱梁人行天桥，一旦一阶竖向振动频率落入行人正常步行频率范围内，极易诱发行人舒适度问题，严重者甚至影响人行天桥的安全与正常使用。

解决简支钢箱梁人行天桥舒适性问题的方法主要有：增加梁高、改变结构支撑体系(如门式刚架)、采用组合结构体系(在梁体上方两侧增设桁架)等增加结构自身刚度的频率调整法[1-3]，使其竖向基频超过3 Hz；在人行天桥上附加耗能装置增大结构的阻尼，较多采用调谐质量阻尼器(TMD)来降低人行天桥在同等人流量下的振动幅值[4-7]。

现有人行天桥竖向减振用TMD的阻尼形式主要有杆式液体黏滞阻尼器[8]、锅式黏滞阻尼器[9]等。但TMD中的黏滞阻尼器存在易漏油、养护困难，以及阻尼系数可能受温度的影响等问题。此外，该类TMD的阻尼在后期均很难调节。最近，汪志昊等[10]研发了耐久性较好的电涡流阻尼TMD，通过模型试验验证了其对人行天桥的减振效果[11]，并已成功用于登机桥人致振动控制工程[12]。电涡流阻尼应用于TMD的突出优点有[10]：TMD的阻尼元件与运动质量块无需直接接触，无任何机构摩擦阻尼；阻尼器内无流体，无需密封件，不会出现任何漏液；阻尼器无附加刚度，不会影响TMD的频率参数，实现了TMD刚度与阻尼的完全分离。但现有电涡流TMD的磁路较为简单，易漏磁，且永磁铁裸露在外，易引发耐久性问题。另外，现有TMD往往难以满足既有人行天桥减振对TMD装配与安装提出的较高要求[13]。

针对既有人行天桥竖向减振用TMD的不足，本文研制了一种结构紧凑、磁路合理、便于现场装配的永磁式竖向电涡流TMD，有望用于工程实际。

1 永磁式电涡流阻尼

当运动非磁性导体切割永磁铁磁力线时，穿过导体的磁通量就会发生连续的变化，根据法拉第电磁感应定律，导体内部就会形成类似漩涡的电流(简称：电涡流)，导致振动能量被导体的电阻热效应逐渐消耗，这就是电涡流阻尼的产生机理[14]。根据电涡流阻尼原理，应用于实际减振工程的既有永磁式电涡流阻尼TMD[10,12,15-16]均是将N、S极交错布置的永磁铁固定在调谐质量块外侧，随质量块同步运动，将非磁性导体铜板独立安装固定在永磁铁外侧，为增强导体板的磁感应强度往往还在导体铜板外侧附加导磁钢板，如图1所示。该类TMD采用的电涡流阻尼装置附加质量偏大，横向尺寸过宽，且永磁铁外漏既影响美观，增加了磁场泄露，也不利于永磁铁的耐久性防护。

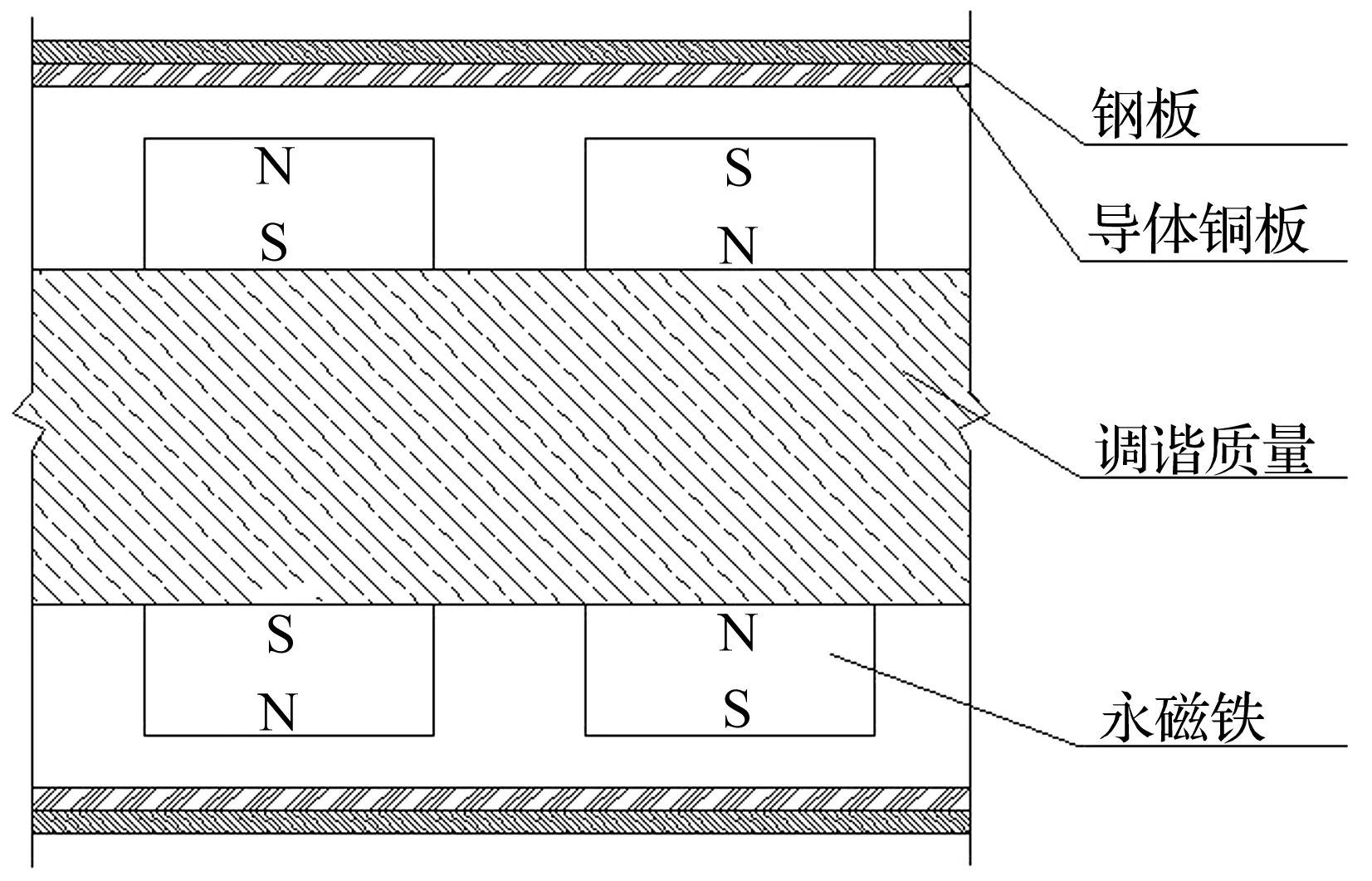
图1 现有竖向TMD电涡流阻尼构造形式Fig.1 Available configurations of eddy-current damping in a vertical TMD

本文拟研制的新型竖向永磁式电涡流阻尼TMD，将永磁铁安装在TMD运动质量块(钢板)内部，永磁铁N/S极交错，形成近似稳定的均匀磁场，导体铜板在稳定磁场中心区域沿竖向相对运动，导体铜板无需设置附加钢板，如图2所示。该TMD电涡流阻尼装置整体结构紧凑、简洁，磁路明确，永磁铁组嵌入在TMD质量块内部易于防护，同时有效提高了TMD运动质量与总质量的比值。新型TMD与传统TMD相关性能比较见表1。

图2 竖向TMD新型电涡流阻尼构造形式Fig.2 Proposed configurations of eddy-current damping in a vertical TMD

性能参数传统TMD新型TMD电涡流阻尼效率一般(导体板后无钢板)、良好(导体板后有钢板)较好耐久性一般好装配性一般好横向尺寸偏大适中有效振动质量比偏小适中

2 装配式竖向电涡流TMD样机设计与制作

2.1 TMD样机参数

笔者曾参与调研了绵阳市部分简支钢箱梁人行天桥的振动情况，在行人激励下这些人行天桥的振动响应均以一阶竖向弯曲振动为主[17]，表2列出了行人舒适度不满足要求的典型人行天桥动力参数。从表2可以看出，主跨40 m左右的简支钢箱梁人行天桥总质量约100 t，主跨超过40 m后第1阶竖向自振频率低于3 Hz，相应的模态质量不超过结构总质量的50%。采用TMD进行减振设计时，若TMD质量比取1%，则TMD运动质量仅需500 kg。因此，简支钢箱梁人行天桥结构及其人致振动特点尤其适用TMD减振。

不失钢结构人行天桥减振的一般性，本文拟研制的新型竖向永磁式电涡流TMD样机，运动质量240 kg，设计频率3.94 Hz、阻尼比7.00%，据此计算得到的TMD刚度系数、阻尼系数分别为146.93 kN/m、0.83 kNs/m。

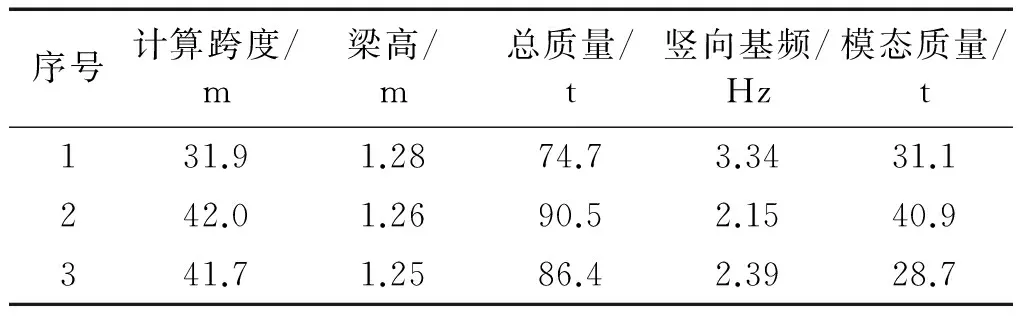
表2 典型钢结构人行天桥动力参数

2.2 电涡流阻尼初步设计

电涡流阻尼系数ce简化公式[10]：

ce=σδSB2

(1)

式中:σ表示导体的导电系数；δ与S分别表示导体的厚度与表面积；B表示导体板表面主磁感应强度的大小。

由式(1)可知，同等条件下，导体板的导电性越好，产生的电涡流阻尼就会越大。因此，本文选取具有较高导电系数、价格相对适中的紫铜作为导体板材料，且导体铜板厚度δ取10 mm。试验采用性价比较好的N40牌号钕铁硼(NdFeB)矩形永磁铁(长、宽、高尺寸分别为50 mm、50 mm、25 mm)，其主要性能参数有：剩磁感应强度1.2T；矫顽力与内禀矫顽力分别为9.3×105Am-1，9.5×105Am-1；最大磁能积为3.2×105Jm-3。

对应目标阻尼系数0.83 kNs/m，由式(1)计算得到永磁铁磁化表面积为0.29 m2，样机共设12块永磁铁，实际磁化表面积为0.03 m2。永磁铁均匀布置在导体铜板两侧，两侧永磁铁完全对称布置，构成6组永磁铁(将两侧各1块对称布置的永磁铁定义为1组)，每侧按上下两排布置，永磁铁与导体铜板布置见图3所示。特斯拉计测试结果显示导体铜板表面(距离单块永磁铁5 mm处)主磁感应强度平均值为0.22 T，据此计算得到电涡流阻尼系数0.84 kNs/m，满足初步设计要求。

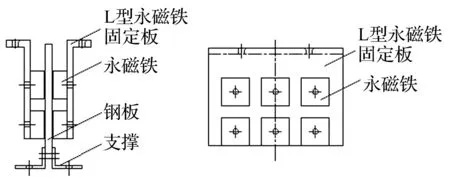
图3 电涡流阻尼器构造示意图Fig.3 Schematic configuration of an eddy current damper

2.3 TMD制作

拟研制的竖向电涡流TMD构造见图4所示， TMD运动质量块套装在固定于下底板的导轴上，并由套装在导轴上的螺旋压簧支撑，导轴顶端安装有限位板。该TMD主要构造特征：TMD运动质量块由下向上依次叠放有5片钢板a、1片钢板b、1片钢板c、1片钢板d和1片钢板e；钢板c的中部预留有安装L型永磁铁固定板(见图3)的槽口；L型永磁铁固定板上安装有永磁铁，相应永磁铁组位于钢板a、b中部形成的矩形腔室内；2块L型永磁铁固定板之间安装有固定在下底板上的导体铜板；在钢板d的导轴孔内设置有直线轴承。

图4 竖向电涡流TMD构造示意图Fig.4 Schematic configuration of a vertical eddy-current TMD

竖向电涡流TMD组装按照从下到上、从内到外的顺序进行，简要装配步骤(图5)如下：

1)准备下底板，装配导轴、螺旋弹簧，固定导体铜板，见图5(a)，然后临时安装钢板a～c；

2)装配L型永磁铁固定板，将两排永磁铁固定在L型永磁铁固定板上，永磁铁上下、左右间距相同，均为25 mm(即永磁铁长度的一半)，且导体铜板两侧的永磁铁完全对称布置，单块L型永磁铁固定板安装示意见图5(b)；

3)将2块L型永磁铁固定板固定于钢板c的预留槽口，见图5(c)；

4)依次安装图5(d)所示的钢板d、直线轴承以及钢板e，接着通过螺杆螺栓将钢板a～e连接为整体构成TMD的运动质量块，然后卸除钢板a下面的临时垫块；

5)安装限位板及固定螺母，见图5(e)。

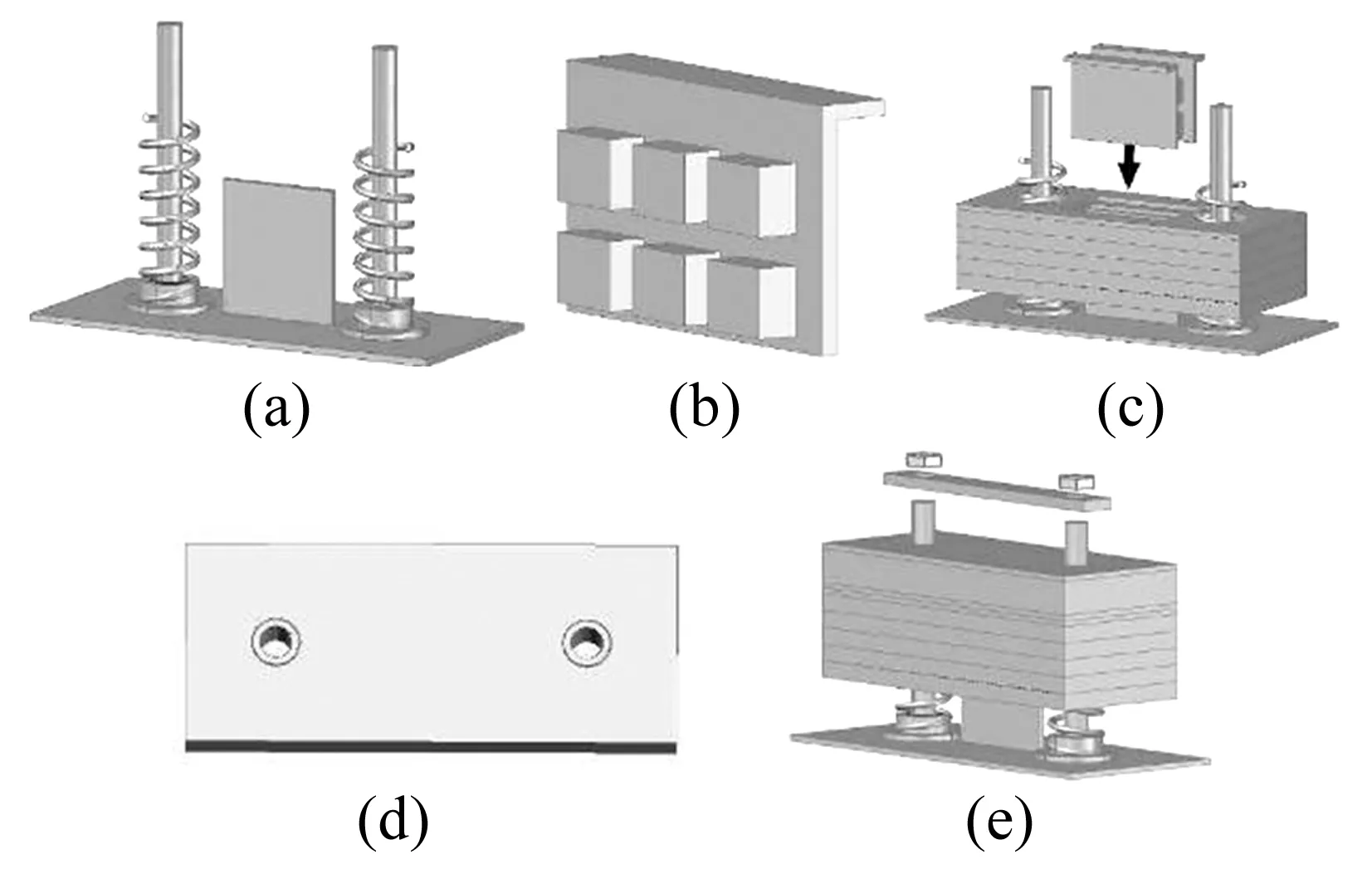
图5 竖向电涡流TMD装配示意图Fig.5 Prefabricated schematic of a vertical eddy-current TMD

经过多次试验最终研制的竖向电涡流TMD样机如图6所示，除永磁铁、直线轴承需要采购外，TMD其余部件均先在工厂预制，然后运至现场进行装配，拆卸方便，便于对TMD的频率与阻尼参数根据工程需要进行适当调整。

图6 竖向电涡流TMD样机Fig.6 Overview of a vertical eddy-current damping TMD

3 TMD性能测试与分析

3.1 测试工况

为明确电涡流阻尼的影响因素，对TMD样机开展了不同工况的阻尼参数测试：

1)工况1，测试TMD的固有阻尼比；

2)工况2，安装1组永磁铁，明确单组永磁铁产生的电涡流阻尼大小；

3)工况3～5，安装2组永磁铁，主要考察相邻永磁铁间距以及排列方式(水平或竖向)对电涡流阻尼效率的影响；

4)工况6～7(图7)，安装3组永磁铁，主要考察相邻永磁铁极性(同侧永磁铁N/S极交错布置或同极布置)对电涡流阻尼效率的影响；

5)工况8～9，安装4组永磁铁，主要考察相邻永磁铁间距对电涡流阻尼效率的影响；

6)工况10，测试TMD安装6组永磁铁产生的电涡流阻尼比，验证设计目标是否实现。

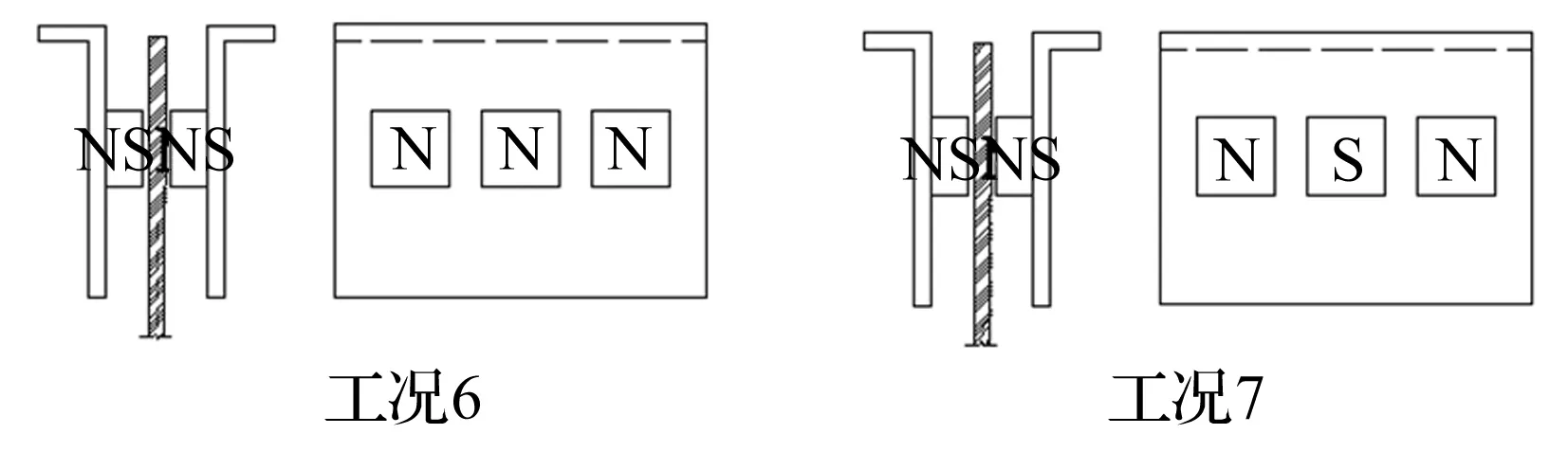
图7 工况6、7永磁铁布置示意图Fig.7 Locations of permanent magnets for case 6 and 7

表3给出了TMD各测试工况永磁铁组数与安装位置说明，其中永磁铁位置编号见图8定义。除工况7外，其它工况单块L型永磁铁固定板上永磁铁均同极布置。

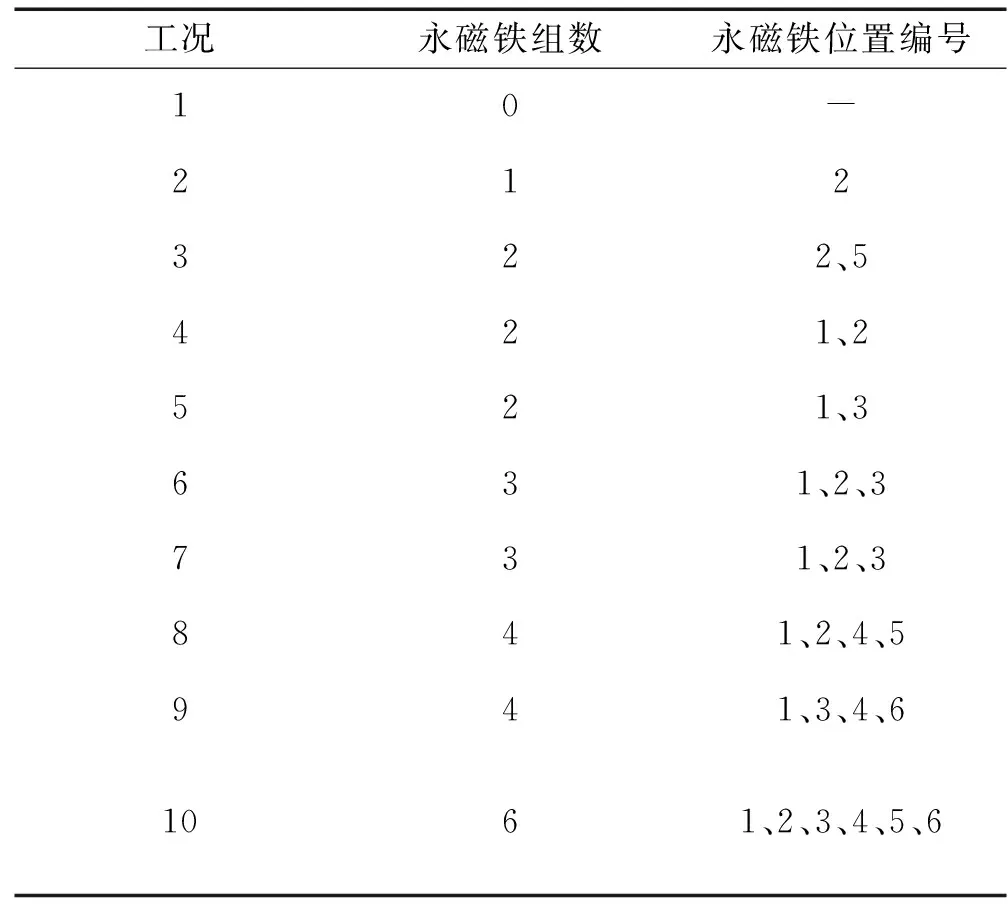
表3 各工况永磁铁安装位置

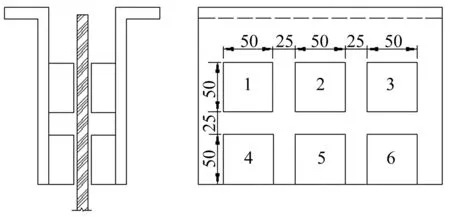
图8 永磁铁布置示意图(单位：mm)Fig.8 Locations schematic of permanent magnets

TMD阻尼比测试采用自由振动法，各工况测试时均将TMD初始位移置于相同位置(振幅1.5 cm)，然后瞬间自由释放，采用INV9828型ICP加速度传感器通过INV3018A型振动信号采集仪记录TMD的自由振动加速度衰减时程曲线。

3.2 测试结果与分析

图9(a)与(b)分别给出了TMD不安装与安装6组永磁铁(永磁铁与导体铜板之间的净距离即磁场间隙5 mm)的自由振动加速度衰减时程曲线。从图9可以看出：TMD的机构固有阻尼较低，等效黏滞阻尼比仅有0.90%，电涡流阻尼起绝对作用。此外，试验识别的TMD固有频率为4.09 Hz，基本处于设计值的目标范围内。

图9 TMD自由振动加速度衰减时程曲线Fig.9 Free vibration time histories of the TMD’s acceleration

表4给出了TMD各工况的实测阻尼比与附加阻尼比，其中由电涡流效应产生的附加阻尼比通过实测阻尼比与机构固有阻尼比的差值计算得到。综合表4与表3分析可知：

1)对比工况3、4、5(2组永磁铁)发现：工况4附加阻尼比最大，其次是工况5，而工况3最小；以工况2(单组永磁铁)结果作为基准，工况3、4与5分别是工况2附加阻尼比的1.69倍、2.56倍、1.96倍。这是由于：2组永磁铁水平间距较大(如工况5的2a，a表示永磁铁长度)时，相邻永磁铁的磁路几乎完全独立，相应附加阻尼比接近单组永磁铁的2倍；2组永磁铁间距较小(如工况3竖向间距0.5a，工况4水平间距0.5a)时，相邻永磁铁磁路耦合作用较强，水平耦合作用较强时(工况4)，有助于增大导体铜板处的水平面磁感应强度，该部分磁感应强度分量与导体板的相对运动速度方向垂直，有利于增大电涡流阻尼，而竖向耦合作用较强时(工况3)，将增大导体铜板处的竖直面磁感应强度，该部分磁感应强度分量与导体板的相对运动速度方向平行，不会产生电涡流阻尼，导致电涡流阻尼效率下降。

2)对比工况6、7(3组永磁铁)发现：同侧永磁铁同极布置(工况6)时附加阻尼比是N/S极交错布置(工况7)时的1.86倍，可见同侧永磁铁同极布置时电涡流效率更高，除特殊说明外本文永磁铁均采用同侧极性相同、不同侧极性相反的布置方式。这是由于：同侧永磁铁N/S极交错布置时，磁路变短，磁力线将主要聚集在远离导体铜板的钢板内部，导致穿过导体铜板的磁力线减小。

3)对比工况8、9(4组永磁铁)发现：工况9的电涡流阻尼效率相对较高，但工况8、9的附加阻尼比均不到相应工况4、5(2组永磁铁单排布置)的2倍。这同样是由于永磁铁之间的水平耦合作用有助于增大电涡流阻尼效率，而永磁铁之间的竖向耦合作用将降低电涡流阻尼效率。值得注意的是，工况6(3组永磁铁单排布置)与工况8、9(4组永磁铁分两排布置)的附加阻尼比对比最能说明永磁铁位置对电涡流阻尼效率的显著影响，工况6以数量较少的永磁铁组却实现了较大的电涡流阻尼。

4)通过工况10的附加阻尼比反算得到电涡流阻尼系数实测值0.51 kNs/m，仅为阻尼系数设计值0.84 kNs/m的61%，表明由于磁泄露与电涡流边界效应简化计算公式(1)过高估计了电涡流等效阻尼系数。

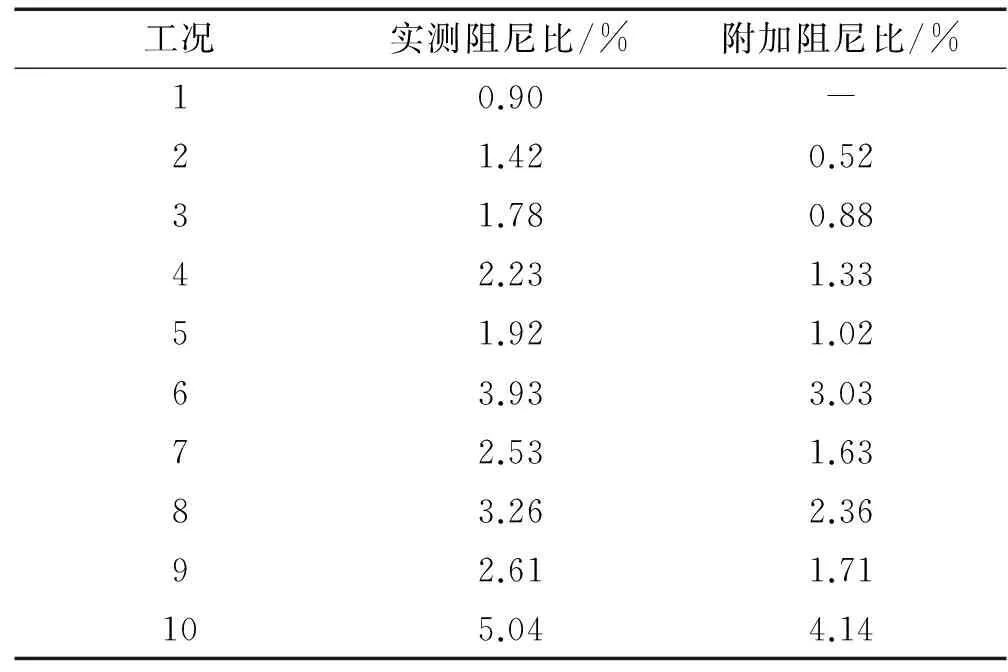
表4 TMD阻尼比测试结果

4 电涡流阻尼磁路有限元分析

4.1 电涡流阻尼磁路仿真分析

为进一步明确永磁铁间距及其极性布置对电涡流阻尼大小的影响规律，印证TMD样机阻尼参数实测结果，采用二维磁场有限元分析软件FEMM对包含两组永磁铁的电涡流阻尼装置(图10)进行了平面有限元分析。永磁铁间距b在0.1a到1.5a之间变化，典型磁路如图11所示。由图11可以看出：磁路磁力线最密集的区域位于永磁铁后的固定钢板，其次为正对永磁铁磁极的导体板区域，且该区域基本处于均匀磁场内。为便于对比分析，图12、13分别给出了永磁铁不同间距下主磁感应强度By在导体板中心线与边缘线上的分布情况。

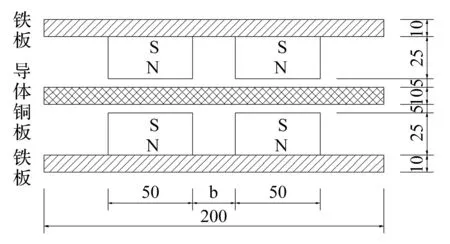
图10 永磁铁与导体板的平面布置图(mm)Fig.10 Layout of permanent magnets and conductive plates(mm)

图11 磁路概况图Fig.11 Schematic of magnetic circuit

图12 导体板中心线主磁感应强度分布随永磁铁间距变化Fig.12 Magnetic induction intensity distribution along the center line of the conductive plate with different distance between permanent magnets

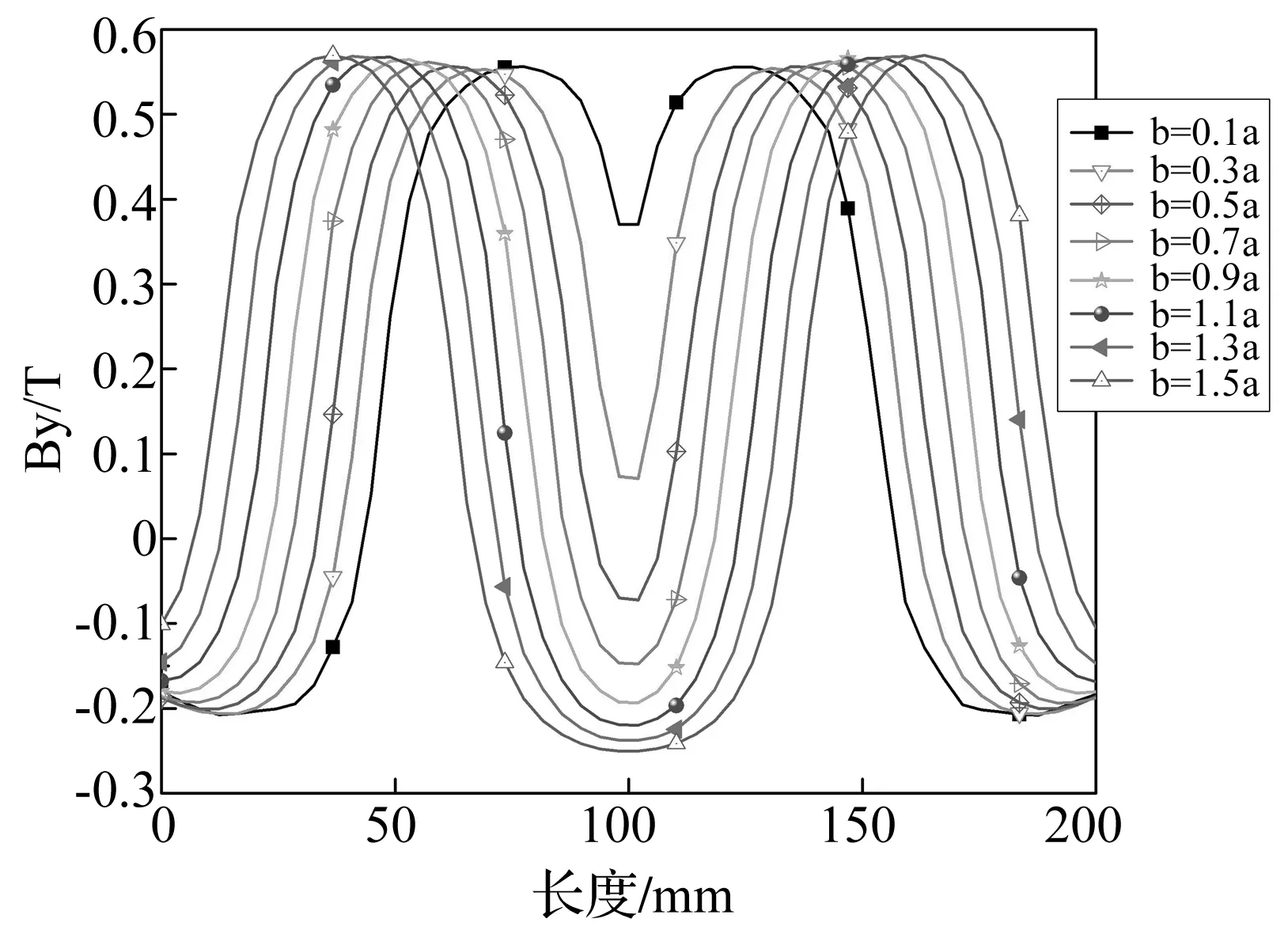
图13 导体板边缘线主磁感应强度分布随永磁铁间距变化Fig.13 Magnetic induction intensity distribution along the edge line of the conductive plate with different distance between permanent magnets

综合图12、13可知：主磁感应强度在导体板中心与边缘处几乎相同，进一步表明了导体板区域近似均匀磁场的形成；当永磁铁间距小于0.5a时，永磁铁中间间隔区域导体铜板处By为正值，距离越近，永磁铁之间的耦合作用越明显；当永磁铁间距大于0.5a时，永磁铁中间间隔区域导体铜板处By开始小于零，表明永磁铁之间的耦合作用开始减弱；当永磁铁间距进一步增加到0.9a后，永磁铁之间几乎不存在耦合作用。这些现象与TMD样机电涡流阻尼测试结果可以很好的相互印证。

4.2 电涡流阻尼力学性能仿真分析

为进一步直接获得TMD电涡流阻尼的力学性能，采用COMSOL软件三维电磁场瞬态分析法[18]对电涡流阻尼的等效阻尼系数进行了仿真分析计算。图14对比了表3工况2～10电涡流阻尼等效阻尼系数实测与仿真值，由图可知：电涡流阻尼等效阻尼系数仿真分析结果与实测值较为吻合，但个别工况误差偏大。误差主要来源：① 仿真分析所需的永磁体相关性能参数不够精确，且仿真分析时忽略了永磁铁中间开孔(便于固定)影响；② 实测阻尼系数通过TMD的附加阻尼比反算得到，而附加阻尼比识别本身会存在一定误差，尤其是当TMD阻尼较大时，基于自由衰减振动信号时域识别阻尼比会带来较大误差。

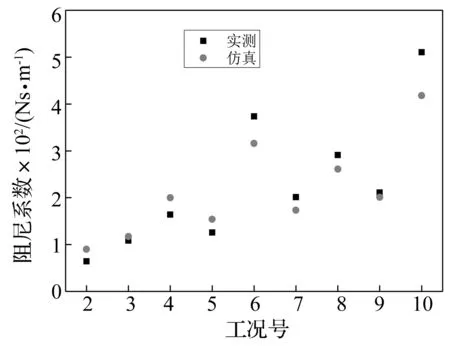
图14 各工况电涡流阻尼等效阻尼系数仿真与实测值对比Fig.14 Comparisons of eddy-current damping coefficients in different case between simulation analysis and test

5 电涡流阻尼设计建议

鉴于简化计算公式(1)过高估计了电涡流等效阻尼系数，建议初步设计时偏保守的在式(1)计算结果乘以0.5的折减因子，然后采用三维磁场有限元分析方法进行校核。为便于竖向电涡流TMD的工业化生产，电涡流阻尼初步设计时也可将一组N/S极相对布置、相距20 mm的N40 NdFeB矩形永磁铁(长、宽、高尺寸分别为50 mm、50 mm、25 mm)，中心插入有10 mm厚的导体铜板定义为板式电涡流阻尼基本单元(对应表3工况2)，将目标电涡流阻尼系数除以该工况实测的阻尼系数64.26 Ns/m即可得到板式电涡流阻尼基本单元的数量，也即永磁铁组的数量。考虑到磁路优化后，电涡流阻尼耗能效率将会有一定程度的提高，该设计也具有一定的保守性，为电涡流阻尼在满足设计目标的前提下一定范围内的适当调节提供了保证。

为提高本文竖向TMD的电涡流阻尼效率，综合TMD样机阻尼比测试结果与磁场有限元分析可知：同侧永磁铁极性宜相同、不同侧永磁铁极性宜相反布置；永磁铁水平间距宜取0.5a(25 mm)以内，竖向间距宜取a(50 mm)以上，以分别增强或削弱永磁铁之间的水平或竖向磁场耦合作用。

6 结 论

本文基于电涡流阻尼研制了一种面向钢结构人行天桥减振应用的新型竖向TMD样机，综合样机电涡流阻尼性能测试与磁场有限元分析，给出了电涡流阻尼磁路优化设计建议。主要结论有：

(1)研发的新型竖向电涡流TMD样机结构紧凑，现场装配简单，耐久性高，且电涡流阻尼具有较大的耗能效率，预计在钢结构人行天桥减振领域具有广泛的应用前景。

(2)获得了竖向TMD电涡流阻尼的合理构造：导体铜板两侧的矩形永磁铁组宜采用同侧极性相同、不同侧极性相反的布置方式；安装空间不受限时，永磁铁宜以水平(单排)布置为主，间距控制在0.5a以内；永磁铁必须布置2排或多排时，上下2排间距不宜小于a。

(3)提出了一套完整的竖向电涡流TMD阻尼构件设计流程，首先应用板式电涡流阻尼基本单元估算永磁铁组数量，然后利用二维磁场有限元分析进行磁路优化设计，最后采用三维电磁场有限元分析方法校核电涡流阻尼等效阻尼系数。

[ 1 ] 刘志才, 唐颖. 人行天桥竖向振动控制[J]. 城市道桥与防洪, 2008(12): 32-36. LIU Zhicai, TANG Ying. Vertical vibration control of walking bridge [J]. Urban Roads Bridges and Flood Control, 2008(12): 32-36.

[ 2 ] 李前名. 车站钢箱梁旅客天桥的竖向振动控制[J]. 铁道建筑, 2013(5): 19-21. LI Qianming. Vertical vibration control of a station footbridge with steel box girder [J]. Railway Engineering, 2013(5): 19-21.

[ 3 ] 熊桂开, 陈翰新. 一座钢人行桥优化设计[J]. 城市道桥与防洪, 2014(10): 99-101. XIONG Guikai, CHEN Hanxin.Optimization design of a steel footbridge [J]. Urban Roads Bridges and Flood Control, 2014(10): 99-101.

[ 4 ] 陈政清, 刘光栋. 人行桥的人致振动理论与动力设计[J]. 工程力学, 2009, 26(增刊2): 148-159. CHEN Zhengqing, LIU Guangdong. Pedestrian-induced vibration theory and dynamic design of footbridges [J]. Engineering Mechanics, 2009, 26(Sup2): 148-159.

[ 5 ] 樊健生, 陈宇, 聂建国. 人行桥的TMD减振优化设计研究[J]. 工程力学, 2012, 29(9): 133-140. FAN Jiansheng, CHEN Yu, NIE Jianguo. Optimum design of tuned mass damper for footbridge [J]. Engineering Mechanics, 2012, 29(9): 133-140.

[ 6 ] 王立彬, 花杰, 刘康安, 等. 大跨度人行桥TMD减振设计[J]. 世界桥梁, 2013, 41(6): 6-10. WANG Libin, HUA Jie, LIU Kangan, et al.Design of tuned mass dampers for long-span footbridges [J]. World Bridge, 2013, 41(6): 6-10.

[ 7 ] 李晓玮, 何斌, 施卫星. TMD减振系统在人行桥结构中的应用[J]. 土木工程学报, 2013, 46(增刊1): 245-250. LI Xiaowei, HE Bin, SHI Weixing. Application of TMD seismic vibration control system in the bridge structures [J]. China Civil Engineering Journal, 2013, 46(Sup1): 245-250.

[ 8 ] WEBER B, FELTRIN G. Assessment of long-term behavior of tuned mass dampers by system identification [J]. Engineering Structures, 2010(32): 3670-3682.

[ 9 ] 尹学军, 王建立, 高星亮, 等. 基于舒适度的钢结构TMD振动控制技术[J]. 建筑结构, 2011, 41(增刊1): 1394-1398. YIN Xuejun, WANG Jianli, GAO Xinliang, et al.Vibration control of steel structure with TMD to increase human comfort [J]. Building Structures, 2011, 41(Sup1): 1394-1398.

[10] 汪志昊, 陈政清. 永磁式电涡流调谐质量阻尼器的研制与性能试验[J]. 振动工程学报, 2013, 26(3): 374-379. WANG Zhihao, CHEN Zhengqing. Development and performance tests of an eddy-current tuned mass damper with permanent magnets [J]. Journal of Vibration Engineering, 2013, 26(3): 374-379.

[11] 汪志昊, 华旭刚, 陈政清, 等. 基于微型永电磁式涡流阻尼TMD的人行桥模型减振试验研究[J]. 振动与冲击, 2014, 33(20): 129-132. WANG Zhihao, HUA Xugang, CHEN Zhengqing, et al. Experimental study on vibration control of a model footbridge by a tiny eddy-current tuned mass damper with permanent magnets [J]. Journal of Vibration and Shock, 2014, 33(20): 129-132.

[12] 蒙华昌, 杨超, 华旭刚, 等. 电涡流TMD应用于登机桥人致振动控制的研究[J]. 预应力技术, 2015(1): 14-17. MENG Huachang, YANG Chao, HUA Xugang, et al. Application of eddy-current TMD to pedestrian induced vibration control of aero-bridge [J]. Prestress Technology, 2015(1): 14-17.

[13] 刘海燕, 陈开利. 在既有人行天桥栏杆上设置薄型TMD进行减振[J]. 世界桥梁, 2004(1): 69-73. LIU Haiyan, CHEN Kaili.In existing pedestrian bridge railing set thin shaped TMD damping [J]. World Bridge, 2004(1): 69-73.

[14] SODANO H A, BAE J S. Eddy current damping in structures [J]. The Shock and Vibration Digest, 2004, 36(6): 469-478.

[15] 雷旭, 牛华伟, 陈政清, 等. 大跨度钢拱桥吊杆减振的新型电涡流TMD开发与应用[J]. 中国公路学报, 2015, 28(4): 60-68. LEI Xu, NIU Huawei, CHEN Zhengqing, et al.Development and application of new type eddy current TMD for vibration control of hangers of long-span steel arch bridges[J]. China Journal of Highway and Transport, 2015, 28(4): 60-68.

[16] 汪志昊, 陈政清, 王建辉. 钢拱桥刚性细长吊杆减振用调谐质量阻尼器的试验研究[J]. 科学技术与工程, 2013, 13(19): 5555-5560. WANG Zhihao, CHEN Zhengqing, WANG Jianhui. Experimental studies on tuned mass dampers for vibration control of rigid slender suspenders in steel arch bridges[J]. Science Technology and Engineering, 2013, 13(19): 5555-5560.

[17] 华旭刚, 陈政清. 绵阳市七座人行天桥动力特性分析与减振措施建议[R]. 长沙: 湖南大学风工程试验研究中心, 2011.

[18] 肖登红, 潘强, 何田. 一种新型电涡流阻尼器及阻尼性能研究[J]. 噪声与振动控制, 2014, 34(6): 197-201. XIAO Denghong, PAN Qiang, HE Tian. Design and analysis of a novel eddy current damper [J]. Noise and Vibration Control, 2014, 34(6): 197-201.

Tests for a prefabricated vertical TMD with eddy-current damping

WANG Zhihao, ZHANG Chuang, ZHOU Jiazhen, XU Zhouyuan

(School of Civil Engineering and Communication, North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

To meet vibration mitigation requirements of long-span urban steel footbridges, a novel vertical eddy-current tuned mass damper (TMD) was developed, it was compact and easy to assemble on site. On the basis of damping parameters test results of the TMD and magnetic field distribution of the eddy-current damping using the finite element analysis, the preliminary design method and the optimal magnetic circuit of eddy-current damping in a vertical TMD were put forward. The results showed that the developed TMD has excellent damping performances and high durability, it is easy to assemble, it is quite feasible for practical application. Moreover, the optimal magnetic circuit configuration for eddy-current damping in a vertical TMD was obtained. It was shown that rectangular permanent magnets on the same side of a copper plate should be the same polarity, while permanent magnets on the different sides should be the opposite polarity; permanent magnets are set in only one row, the horizontal distance between permanent magnets should be less than half of the length of permanent magnets; if permanent magnets must be arranged in two or more rows, the vertical distance between permanent magnets should be more than the length of permanent magnets.

footbridge; vibration control; tuned mass damper (TMD); eddy current damping; magnetic circuit optimization

国家自然科学基金资助项目(51308214)；国家重点基础研究973计划项目(2015CB057702)；河南省高等学校青年骨干教师资助计划(2015GGJS-104)

2016-02-23 修改稿收到日期：2016-05-08

汪志昊 男，博士，副教授，1980年9月生

TU352.1

A

10.13465/j.cnki.jvs.2017.01.003