数学课堂观察的视角：价值、问题与方法——评曹伟林老师的“4.1从问题到方程”教学

■钱德春

数学课堂观察的视角：价值、问题与方法
——评曹伟林老师的“4.1从问题到方程”教学

■钱德春

“教什么”“为什么教”和“怎么教”是课堂教学永恒的话题，“教什么”即教学内容与问题；“为什么教”即教学价值；“怎么教”即教学方法。教者的这节课以对教材独到的理解、对学情充分的把握和教学过程的精彩演绎，在“教育价值”“问题解决”“教学方法”三个方面给予我们以完美诠释。

一、教育价值引领数学教学

裴光亚先生说：“教育价值是教学设计的灵魂。”为什么要安排这一节课？也就是，本节课内容的教学价值何在？这里通过表格对小学和本节课“方程”部分内容进行比较（相同部分省略）：

一是为什么要建立“一元一次方程”概念。所有数学概念大多为解决和表达新问题、新现象，或揭示数学本质而建立，并随着数学的发展不断优化与完善。从表格中发现：小学教材的章节标题是“简易方程”，给出了最上位的“方程”概念，有“简易”就有复杂，我们在“解决问题”中遇到了具体的、更复杂的方程，这些方程与其他方程如何区别，又如何表达，这就有必要出现新的定义。这就是“一元一次方程”概念的教学价值，教者通过教学活动让学生有了很好的价值体验。

二是用方程刻画现实世界（即列方程解决问题）的能力有何要求。这方面内容在小学已有接触，用方程解决问题的基本路径是：找相等关系、用含未知数的代数式表示，这在今后的学习中保持不变，那么这里“反复让学生列方程”的价值何在？我们知道，“找相等关系列方程”始终是运用方程模型解决现实问题的重点和难点，从小学到初中，方程类型不断增加，分析方法多种多样，问题难度逐步提高。因此，这个过程是学生解决问题能力不断升级的过程，也是一个循序渐进的过程，这正是教学价值所在。犹如小学和初中作文都可以写“有意义的一件事”，能力要求大不一样。可喜的是：教者始终抓住这个关键开展教学活动。

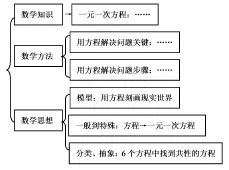
三是数学思想方法如何渗透。从表中发现：小学解方程是用等式的基本性质将方程转化为形如“x=a”的形式，初步感知转化思想。本节课还渗透这样几种思想：从“方程”到“一元一次方程”渗透“一般到特殊”的思想；将6个方程放在一起，通过分类比较，找出具有共性的几种方程，从而建立“一元一次方程”概念，渗透了分类与抽象的思想；通过用方程表示相等关系解决现实问题，让学生感受“模型”思想。从课堂来看，教者做得都非常到位。我们还注意到，教师对数学思想方法的渗透是潜移默化、润物无声的，而不是贴标签式的。

二、问题解决驱动知识建构

建构主义学习理论认为：客观的知识结构通过个体与之交互作用而内化为学生的认知结构。要实现这种内化，必须了解学生的已有认知水平和通过努力能够达到的认知水平。学生在小学五年级下册第一章“简易方程”的学习中，已经初步了解了方程、方程与等式的区别、方程的解、解方程的含义、等式的性质（加、减、乘、除一个数，除数不为0），能够列简易方程解决实际问题的步骤、如何找数量关系等。

教者基于学生已有认知，根据本节课知识、能力要求，将教学内容转化为3个核心问题：一是如何建立一元一次方程概念；二是如何引导学生用方程模型刻画现实问题，并规范解决问题的步骤；三是如何在建构知识的同时渗透数学思想。通过学生自主探究和教师趁机引导，在问题解决中建构知识，并将3个核心问题通过现实情境具体化(求年龄问题)，进而再将问题细化为问题链，启发学生拾级而上，逐步深入探究与思考。

三、教学方法促进数学理解

教学有法，教无定法。教者来自处于教改前沿的洋思中学，他们的“先学后教”课堂教学模式闻名遐迩，也引发不少争议。从这一节课来看，教者充分运用了学习目标领航、学生自主探究、师生问题对话、教师示范引领等多种教学形式，促进学生数学学习。可见洋思课堂教学“先学后教”的内涵得到了丰富与发展。

一是目标领航学习。任何一节课都有明确的目标，教者在引发学生认知冲突后，呈现学习目标：（1）探索多种实际问题中的数量关系，并能用方程描述；（2）了解一元一次方程的概念。这样让学生学有方向，习有目标。课堂目标分显性目标和隐性目标。所谓显性目标，就是呈现给学生的、让学生明白的知识技能和解决问题的能力目标，让学生带着问题和任务学习；另一种目标是隐性的，那就是思维能力以及情感态度价值观目标，这是教者心里明白的潜在目标。

二是探究凸显主体。学生是课堂的主体，自主探究活动是体现学生主体地位的重要载体。课堂上，教者择机安排多次探究活动：通过对“天平和方程”问题的探究，感受“方程就是表达数量关系的‘天平’”；通过对“篮球联赛胜负”提出开放性问题，引导学生自主探究，学生从不同的角度提出不同的问题，列出不同的方程，为建立“一元一次方程”概念作铺垫，进一步感受方程是刻画现实世界的一种模型，同时培养学生数学化的能力。这些教学活动凸显了学生在学习中的主体地位，而教者通过巡视、质疑、启发、追问等手段，引导学生探究、思考与交流，充当了组织者、引导者与合作者的角色。

三是对话促进理解。在问题解决过程中，通过师生对话促进学生数学学习，给笔者留下了深刻的印象。教师捕捉探究活动中即时生成的问题作为对话话题，如：“怎样描述天平所表示的数量之间的相等关系？”“如把你问题中的一个未知量设为x，可得什么方程？”“这个相等关系，信息中哪里给出了提示？”“相等关系抓的是哪个关键句？”“12-x是什么意思？”“方程2x+y=20怎么解释呢？”这一系列问题，引发思维冲突，驱动认知发展，从而在生成的新问题中建构知识、渗透思想、发展能力，这种对话看似无意实则有意，具有生成性、即时性和发展性，是一种无法预约的精彩，充分显示了教者独到的数学理解和深厚的教学功底。另外，师生对话的话题具有开放性和民主性。如“请你根据信息提出一个数学问题”，这是极具开放性的问题，不同的学生对问题信息可能有不同的理解角度，进而提出不同的问题，列出不同的方程，这种对话方式顺应了学生的个性思维与需求。再比如：“老师把时间交还给你们，由你们自己学习探究，好不好？”这种协商的口吻充满了民主平等的氛围，让学生以愉悦的心情投入学习活动。

四是教师示范引领。这是数学教学不可或缺的过程。本节课中，教者善于发现生成性错误资源，通过师生研讨，及时纠错，达到知识内化的目的。当学生列出方程“2x×x=40”时，教者启发学生修正为“2x2=40”；当回到解决课始时的现实问题时，教师通过板书示范，强调“找、设、列、解、验、答”的步骤。因为这个过程在小学是初步感知，学生的认识是模糊的、肤浅的，本节课通过实际问题的解决，对解题过程和步骤初步提出了规范性、完整性、反思性要求，这在能力要求上更上一层。我们还注意到，这些错误和问题资源不是教者先入为主强加给学生的，而是在学习活动中产生的，这样的纠错和规范更能让学生有紧迫感和切身体验。

四、教学设计基于“三个理解”

任何一节优秀课都有值得探讨的地方，正因如此，才体现出其应有的研究价值。概念课如何教学？章建跃先生提出的“三个理解”应该是教学设计的起点，也是课堂教学的归宿，教学设计就要在“理解数学、理解学生、理解教学”的基础上展开。就本节课而言，有两个要点提出来与教者商榷。

一是建立新概念的必要性。为什么要建立概念，这是“理解数学”的问题；学生有什么困惑，这是“理解学生”的问题。在学生根据现实情境列出方程后，教者引导学生通过分类与比较未知数的个数、次数，从而得到“一元一次方程”概念。那么学生会问：为什么要建立这个概念？形式化与结构化是数学的基本特征之一。在所列的6个方程中，方程2x+y=20、x+y=12的解不确定，方程用现有知识无法求解，而其余3个方程与小学学过的简易方程类似，整理后有统一的特征与结构，为了便于表达和交流，必须有一个规范的标准，我们有必要给其命名。这个过程不需花费太多时间，但不可或缺。

二是归纳小结环节的安排。这是“理解教学”的问题。课堂小结是课堂教学的重要组成部分，教者提出“通过本节课的学习，你有哪些收获”的问题引导学生小结，但这样的问题有些让学生无所适从。笔者以为：课堂小结是一节课的点睛之笔，必须要有明确的指向性，并引导学生用框图等方式将知识、方法、思想结构化（如下图）。本节课小结可提出这样的问题：你学到了什么知识？体会到哪些数学思想方法？你还有什么困惑？进而引导学生建构框图。

（作者为江苏省泰州市教育局教研室初中数学教研员）