委托代理的最优契约安排

徐齐利

(首都经济贸易大学 经济学院，北京100070)



委托代理的最优契约安排

徐齐利

(首都经济贸易大学 经济学院，北京100070)

本文研究代理人的努力信息和市场的行情信息在委托人、代理人、仲裁人之间不同分布时委托代理的最优契约安排及其效应。与帕累托最优时的保险性合同条款相比，(1)在可观察可证实情形下，最优契约安排是设置以固定工资支付最大努力且具有强制效力的保险性合同条款；该情形的最优契约安排因信息完全对称而效率最高。(2)在不可观察不可证实情形下，最优契约安排是设置在固定工资的保险性合同条款的基础上增列产出分成的激励性合同条款；该情形的最优契约安排因信息完全不对称而效率最低。(3)在不可观察但可证实情形下，最优契约安排是设置除固定工资的保险性合同条款加产出分成的激励性合同条款之外再加进对有意偷懒则罚、额外努力则赏的赏罚性合同条款，该情形的最优契约安排因信息部分对称、部分不对称而效率折中。

委托代理；契约安排；合同设计；信息不对称

委托代理的市场主体有三类：委托人、代理人和仲裁人。委托人与代理人之间利益相关；当委托人与代理人之间发生委托代理的利益纠纷时，需提请第三方仲裁人仲裁，故仲裁人应与委托人和代理人之间利益无关。委托代理的市场信息有两类：代理人的努力信息和市场的行情信息。对于委托代理的契约安排问题，根据完全契约与不完全契约的定义[1,2]，本文将委托代理的信息完全对称界定为委托人可观察到代理人的努力程度，并且仲裁人可证实相应努力程度对企业业绩产生的影响(即面对委托代理仲裁需求时，仲裁人能够区分代理人的努力信息和市场的行情信息)，此种信息结构本文将其简称为可观察可证实情形；将委托代理的信息完全不对称界定为委托人不可观察到代理人的努力程度，并且仲裁人也不可证实相应努力程度对企业业绩产生的影响(即面对委托代理仲裁需求时，仲裁人不能够区分代理人的努力信息和市场的行情信息)，此种信息结构本文将其简称为不可观察不可证实情形；将委托代理的信息部分对称、部分不对称界定为委托人不可观察到代理人的努力程度，但仲裁人可证实相应努力程度对企业业绩产生的影响，此种信息结构本文将其简称为不可观察但可证实情形。

本文在张维迎[3]对委托代理Holmstorm-Milgrom模型[4-7]进行赋参简化的基础上研究不同信息结构下委托代理的最优契约安排，并分别从社会福利和成本收益两个视角考察其效应。研究发现：(1)在可观察可证实情形下，最优契约安排是设置以固定工资来支付最大努力的强制性合同条款；该情形的最优契约安排因信息完全对称而效率最高，能够到达帕累托最优。(2)在不可观察不可证实情形下，最优契约安排是设置除固定工资之外还有产出分成的激励性合同条款；该情形的最优契约安排因信息完全不对称而效率最低。(3)在不可观察但可证实情形下，最优契约安排是设置除固定工资加产出分成之外再加进对有意偷懒以惩罚、额外努力以补偿的赏罚性合同条款，该情形的最优契约安排因信息部分对称、部分不对称而效率折中，它相对不可观察不可实证情形则是一个帕累托改进。本文接下来的论述安排如下：首先，为了便于不同情形下最优契约安排的静态比较，考察帕累托最优的契约安排及其效应；然后，依次考察可观察可证实、不可观察不可证实、不可观察但可证实三类情形各自的最优契约安排及其效应；最后，总结并讨论。

二、帕累托最优的契约安排

以量h表示代理人的努力水平，设企业产出水平π与代理人努力水平h之间呈线性关系

π=h+θ,θ～N(0,σ2)

(1)

其中θ为企业所处环境的外生不确定性冲击，服从期望E(θ)=0方差Var(θ)=σ2的正态分布。在此假设下， 企业产出π具有不确定性： 产出期望为E(π)=h， 产出风险为Var(π)=σ2， 产出分布为π～N(h,σ2)。

契约安排的模式是设计线性的劳资合同

s(π)=α+βπ

(2)

其中α为委托人支付给代理人的固定工资，它与企业的产出水平π无关。通常情况下，α>0表示委托人向代理人支付保险；但有时也会有α<0，此时则表示代理人向委托人支付保险；本文只考虑α>0这种常规情形。βπ为委托人支付给代理人的绩效工资，它是企业的产出水平π的β倍。β是代理人从企业产出水平π中享有的份额，它既是代理人的激励杠杆，也是其风险敞口；0<β<1表示代理人分享部分业绩的同时承担部分风险，β=0说明代理人不享业绩也不担风险，β=1表示代理独享业绩和独担风险。

假设委托人风险中性，代理人风险规避。作为剩余索取者的委托人，其期望效用为

E(v(π-s(π))) =E(π-s(π))

=-α+(1-β)h

(3)

对于作为优先索取者的代理人，为了分析的方便，其面对实际收入w时，假设具有不变的绝对风险规避度[8]ρ，即效用函数为

u(w)=-e-ρw

(4)

假设代理人付出努力时发生的货币化成本为c(h)=bh2/2,b>0表示代理人的偷懒倾向。对于付出努力水平为h的代理人在面对企业产出水平为π时的实际收入水平为

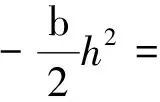
(5)

代理人的实际收入w具有不确定性：期望为E(w)=α+βh-bh2/2， 风险为Var(w)=β2σ2， 分布为w～N(α+βh-bh2/2,β2σ2)。

下面以定义和引理的形式给出随机变量的确定性等价概念及其性质，以便后续分析。

定义：设x为确定变量，y为随机变量，如果作用在x,y上的单调变换u(·)使得u(x)=E(u(y))成立，则称确定变量x为随机变量y的确定性等价。

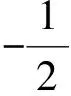
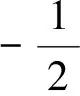
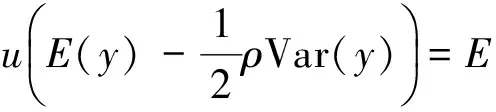
(6)

其中E(y)和Var(y)依次是随机变量y的期望和方差。

针对具有(4)式风险规避特征的代理人，获得(5)式随机性收入w的确定性等价收入为

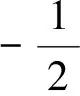
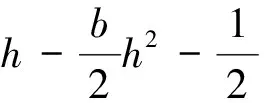
(7)

其中α+βh-bh2/2是代理人的期望收入，ρβ2σ2/2是代理人因承担风险导致的收入损失，称为代理人的风险成本，当β=0时，风险成本为0。代理人最大化(4)式所示的期望效用等价于最大化(7)式所示的确定性等价收入，即

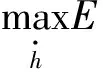
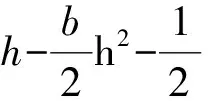
(8)

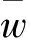
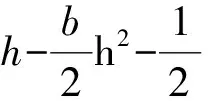
(9)

考虑追求社会福利(委托人的期望收入与代理人的确定性等价收入之和)最大化的契约安排：一方面，为使社会福利尽可能大，由决策变量构成的可能性集需尽量大，也就是约束条件需尽可能少；另一方面，代理人不接受合同，即该项工作没人做，则委托人和代理人在该项目上获得的收入都为0，此时社会福利也为0，这就是说该项工作能够达成、从而获得正的社会福利的契约安排必须满足代理人的个人理性，即参与约束。基于这两方面的考虑，社会福利最大化的契约安排则是下面最优化问题的解

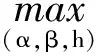
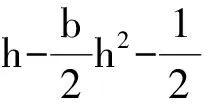
(10)

实际上，作为剩余索取者的委托人，他完全没必要最终支付给代理人的劳动报酬所形成的代理人的确定性等价收入高于其保留收入，也就是说理性的委托人应将参与约束束紧，即等号成立。从而，(10)式所示的优化问题可简化为如下形式：

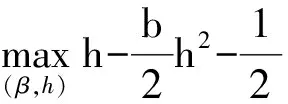
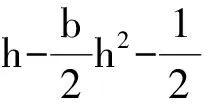
(11)

由(11)式所示优化问题的一阶条件

1-bh=0

ρβσ2=0

以及等式约束得到帕累托最优时代理人的努力水平、享受的产出分成比例和保险金额分别为

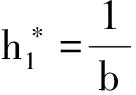
(12)

下面，以命题的形式总结帕累托最优的契约安排及其效应。

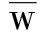
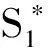
(13)

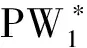
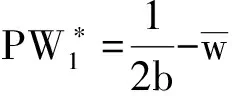
(14)

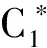
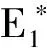
(15)

三、可观察可证实的契约安排

遵行(2)式线性劳资合同的契约安排模式，现在考虑在代理人的努力水平能够被委托人观察到，且该努力导致的产出能够被第三方仲裁机构证实情形下的最优契约安排。

由于代理人的努力水平可观察且由相应努力水平带来的产出可证实，委托人完全可以且应该在契约安排中设定一个对自己最有利的努力水平，并强制代理人按此努力水平从事。这就是说，委托人在寻求使自己利益最大化的契约安排过程中没有必要事先要求代理必须达到何种努力程度，即求解最优契约安排的优化模型中无需设置对代理人的激励约束，只需设置对代理人的参与约束。因此，寻找代理人可观察可证实情形下的最优契约安排问题就转化为求解下列优化模型

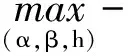
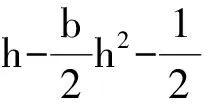
(16)

将束紧的参与约束IR代入目标函数，以消除α，得到优化问题的新形式为

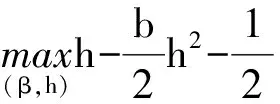
(17)

由(17)式优化问题的一阶条件及束紧的参与约束得到可观察可证实情形下委托人最优契约安排的参数，即代理人的努力水平、享受的产出分成比例和保险金额分别为

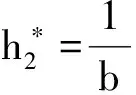
它与帕累托最优的契约安排参数完全一致。进而带给委托人的期望收入、代理人的确定性等价收入、社会的福利水平，以及给代理人带来的努力成本、风险成本和给企业带来的期望产出

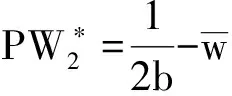
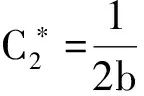
也都与帕累托最优时的契约安排效应完全一致。下面以命题的形式给出可观察可证实情形下最优的契约安排及其效应。

命题2：(1)在代理人的努力水平能够被委托人观察到，且该努力导致的产出能够被第三方仲裁机构证实的情形下，最优契约安排就是设计如下给代理人提供固定工资的具有强制效力的保险性合同条款

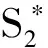
(18)

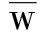
(2)在代理人的努力水平能够被委托人观察到，且该努力导致的产出能够被第三方仲裁机构证实情形下的最优契约安排所产生的福利效应与帕累托最优的契约安排效应相一致。

(3)在此情形下最优的契约安排所产生的成本收益效应也与帕累托最优的契约安排效应相一致。总之，在信息完全对称情况下，由于委托人能够观察到对代理人的努力程度，第三方机构能够证实相应努力程度形成的产出水平，故而形成委托代理的最优契约安排是帕累托最优的。

四、不可观察不可证实的契约安排

在代理人的努力水平不可观察，且由其努力导致的产出水平也不可被第三方机构证实的情形下，契约安排除了满足代理人的个人理性约束外，还应满足对代理人的激励约束，即正因为不能观察到代理人的努力程度而需诱导其选择使自身收入最大的努力水平。还是按照(2)式所示的契约安排模式设计合同，则寻求最优的契约安排参数即是求解下面的优化问题。

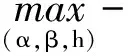
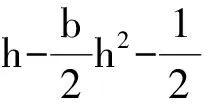
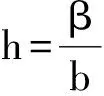
(19)

激励相容约束之所以取h=β/b是因为：代理人从自身利益出发，在给定委托人设置的合同参数(α,β)下，代理人实现自身利益最大化就是寻找最优的努力水平h使其确定性等价收入最大，而代理人使确定性等价收入α+βh-bh2/2-ρβ2σ2/2最大的一阶条件是β-bh=0，即h=β/b；这就是说，在给定委托人设置的合同参数(α,β)下，代理人的最优努力水平为h=β/b，根据逆向归纳法，寻求最优契约安排的委托人在激励相容约束时将代理人的最优努力反应函数h(β)=β/b考虑进来。根据激励约束来取代目标函数中的h，根据束紧的参与约束来取代目标函数中的α，则(19)式的优化问题变形为

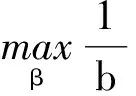
(20)

由(20)式的一阶条件

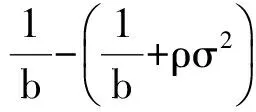
及束紧的约束条件得最优的契约安排参数为

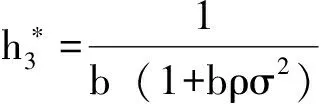
(21)

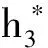
命题3：(1)在代理人的努力水平不可观察且由努力形成的产出水平不可证实的情形下，最优的契约安排就是委托人同代理人签订如下除固定工资的保险性合同条款外再增加产出共享、风险共担的激励性合同条款

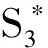
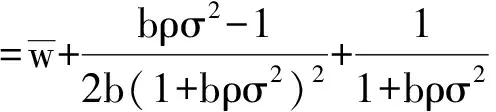
(22)

(2)在代理人的努力水平不可观察且由努力形成的产出水平不可证实的情形下，最优契约安排产生的福利效应为：给委托人带来的期望收入、给代理人带来的确定性等价收入、给社会带来的福利水平分别如(23)式所示

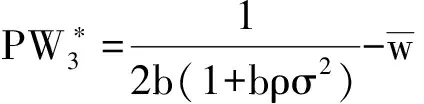
(23)

(3)在此情形下，最优契约安排产生的成本收益效应为：给代理人带来的努力成本、风险成本，以及给企业带来的产出分别如(24)式所示

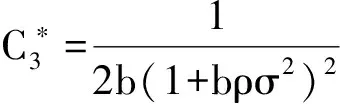
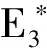
(24)

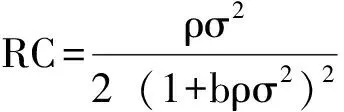
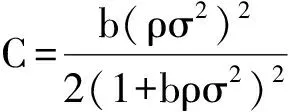
(25)

其中

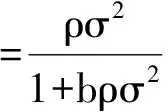
(26)

由此可知，该情形因形成原本不必要的代理成本(AC=ΔRC+(ΔE(π)-ΔC))

(27)

而造成效率损失。

五、不可观察但可证实的契约安排

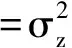
针对能表征代理人努力水平h的工具变量π+γz，委托人还是按照(2)式所示的这一基本的契约安排模式设计合同，如下式

s(π,z)=α+β(π+γz)

(28)

在该契约安排下，代理人承担工作获得合同规定的名义工资扣除因努力导致的货币化成本之后形成的实际风险收入为

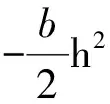
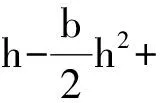
(29)

根据引理，对于具有(4)式风险规避特征的代理人，与该风险收入对应的确定性等价收入为

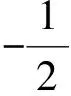
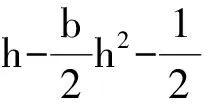
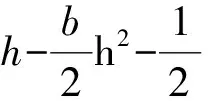
(30)

对于风险中性的委托人，获得具有风险性产出剩余π-s(π,z)的效用即可用期望剩余，称为委托人的期望收入来衡量，如(30)式

E(v(π-s(π,z)))=E(π-s(π,z))

=-α+(1-β)h

(31)

与前述不可观察不可证实情形时委托人寻求最优契约安排参数的逻辑一致，在此不可观察但可证实情形下，无法观察到代理人努力程度的委托人寻求最优契约安排就是求解下面的优化问题

(32)

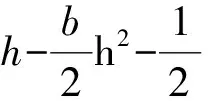
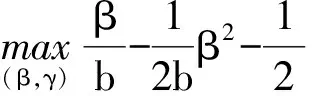
(33)

由(33)式的一阶条件

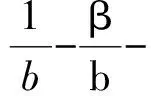
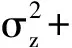
及束紧的约束条件得最优的契约安排参数为

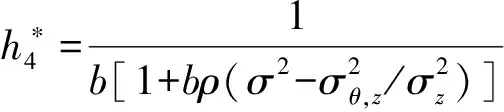
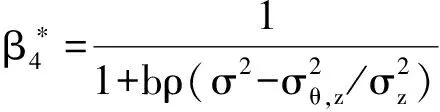
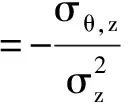
以δ表示外生冲击θ与其充分统计量z之间的相关系数，即δ=σθ,z/(σzσ)，则上述最优的契约安排参数可表示为

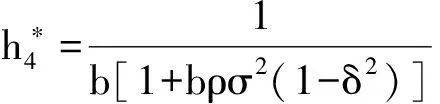
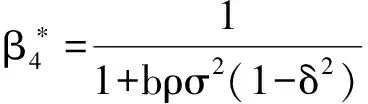
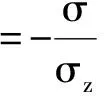
(34)

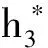
命题4：(1)在代理人的努力水平不可观察但由努力形成的产出水平可证实的情形下，最优的契约安排就是委托人同代理人签订如下除固定工资的保险性合同条款加产出分成的激励性合同条款外还增列对有意偷懒以惩罚、额外努力以补偿的赏罚性合同条款

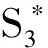
(35)

(2)在代理人的努力水平不可观察但由努力形成的产出水平可证实的情形下，最优契约安排产生的福利效应为：给委托人带来的期望收入、给代理人带来的确定性等价收入、给社会带来的福利水平分别如(22)式所示

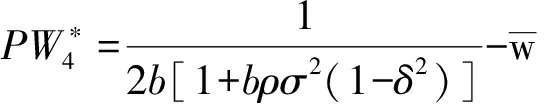
(36)

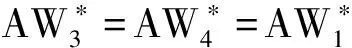
(3)在此情形下，最优契约安排产生的成本收益效应为：给代理人带来的努力成本、风险成本，以及给企业带来的产出分别如(37)式所示

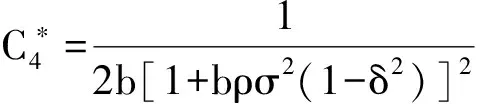
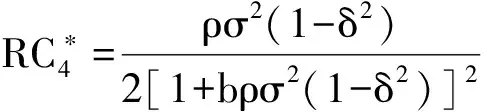
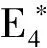
(37)

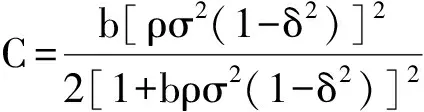
其中

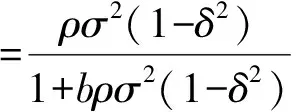
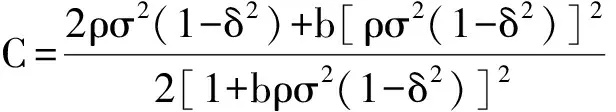
(38)

由此可知，该情形最优契约安排形成原本不必要的代理成本(AC=ΔRC+(ΔE(π)-ΔC))为

(39)

与可观察可证实情形最优契约安排相比，确实因形成了不必要的代理成本而造成效率损失，但与不可观察不可证实情形最优契约安排相比，又因代理成本有所下降而使得效率得以提升。

六、结论与讨论

对于委托代理的最优契约安排问题，本文将代理人的努力信息和市场的行情信息在委托人、代理人、仲裁人之间的对称与不对称分布按照契约的可观察属性和可证实属性归类三种情形，逐一考虑各情形下的最优契约安排及其效应。与帕累托最优时支付固定工资的保险性合同条款相比：(1)在委托人可观察且仲裁人可证实代理人的努力信息和市场的行情信息情形下，最优的契约安排是委托人设置要求代理人付出最大努力程度而获得固定工资的具有强制效力的保险性合同条款；该情形的最优契约安排因信息完全对称而效率最高，从社会福利效应来看它是帕累托最优的契约安排，从成本收益效应来看它是不产生代理成本的契约安排。(2)在委托人不可观察且仲裁人不可证实代理人的努力信息和市场的行情信息情形下，最优的契约安排是委托人给代理人设置固定工资的保险性合同条款之外还让其参与企业风险性产出分成的激励性合同条款；该情形的最优契约安排因信息完全不对称而效率最低，相对可观察可证实情形，从社会福利效应来看代理人的效用不变而委托人的效用损失严重，从成本收益效应来看产生了严重的原本不必要的代理成本。(3)在委托人不可观察但仲裁人可证实代理人的努力信息和市场的行情信息情形下，最优的契约安排是委托人在固定工资的保险性合同条款加对企业风险产出分成的激励性合同条款基础上还加进对代理人有意偷懒以惩、对额外努力以补偿的赏罚性合同条款，该情形的最优契约安排因信息部分对称、部分不对称而效率折中，从社会福利效应来看代理人的效用不变而委托人的效用虽有所损失、但并不严重，从成本收益效应来看较之可观察可证实情形则存在代理成本、但较之不可观察不可证实情形则代理成本较低。

上述最优契约安排及其效应成立的前提有三：(1)代理人努力成本函数中的偷懒倾向b在代理人、委托人、仲裁人三方之间是共同知识。当努力成本函数中的偷懒倾向b为代理人的私人信息、而委托人与仲裁人只能知道代理人偷懒倾向b的分布特征时，上述三类情形下各自的最优契约安排及其效应又将如何是下一步研究的方向。(2)作为风险中性的委托人是最终的剩余索取者。倘若委托人是风险规避者，则他会设置优先获取固定收入的契约安排模式(如委托人将企业承包给代理人而获得无风险的租金)，在此模式下，上述三种情形的最优契约安排及其效应又将如何也是下一步研究的方向。(3)委托人将企业的短期利润或产出作为企业经营的业绩目标。当委托人将企业的长期利润或产出，即企业的价值也纳入进合同条款的设计之中作为企业经营业绩目标时，则代理人会在企业利润与企业价值之间进行权衡，在此模式下，上述三种情形的最优契约安排再将如何也会是下一步研究的方向。

附录：对引理的证明

证明：根据正态分布的性质知E(y)=μ,Var(y)=σ2，下面根据确定性等价的定义，计算变换函数的期望

E(u(y))=E(-e-ρy)

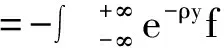
从而引理得证。

[1]Hart O, Holmstrom B. The Theory of Contracts[J]. Working Papers, 1986, 39(4):71-155.

[2]Tirole J.TheTheoryofIndustrialOrganization,Chapter0oftheTheoryofthefirm[M]. Cambridge, Massachusetts: The MIT Press, 1988：15-55.

[3]张维迎. 博弈论与信息经济学[M]. 上海：上海人民出版社，2004：256-262.

[4]Hölmstrom B. Moral hazard and observability[J]. The Bell Journal of Economics, 1979,10(1):74-91.

[5]Holmstrom B, Milgrom P. aggregation and linearity in the provision of intertemporal incentive[J]. Econometrica, 1987, 55(2): 303-328.

[6]Rees R. The Theory of Principal and Agent: Part 1[J]. Bulletin of Economic Research, 1985, 37(1):3-26.

[7]Milgrom B, Milgrom P. Multitask Principal-Agent-Analysis: Incentive Contracts, Asset Ownership, and Job Design[J]. Journal of Law Economics & Organization, 2010, 7(7):24-52.

[8]Varian, H. R.MicroeconomicAnalysis(ThirdEdition)[M]. New York: Norton, 1992：177-189.

(编辑：佘小宁)

Optimal contract arrangement of principal and agent

Xu Qili

(SchoolofEconomics,CapitalUniversityofEconomicsandBusiness,Beijing100070,China)

Optimal contract arrangements and their effects were studied in different distributions of the agent's effort information and market stochastic information among principal, agent and arbitrator. Compared with the Pareto optimal, (1) in observable and verifiable case, the optimal contract arrangement is setting mandatorily insurance terms in the form of fixed return to the maximum effort, and it is the most efficient because of complete symmetry of information; (2) in unobservable and unverifiable case, the optimal contract arrangement is setting incentive terms with risky output to share in addition to insurance terms, and it is least efficient because of complete asymmetry of information; (3) in unobservable but verifiable case, the optimal contract arrangement is setting rewarding-or-publishing terms in order to reward excess effort and punish intentional laziness in addition to the insurance and incentive terms, and it is moderately efficient because of partial symmetry and partial asymmetry of information.

Principal and agent; Contract arrangement; Contract design; Asymmetric information

2016-12-22

徐齐利(1986-)，男(汉)，湖北孝感人，统计师，博士研究生，主要从事微观经济理论、产业组织理论方面的研究。

首都经济贸易大学研究生学术新人计划(2015XSXR006)；首都经济贸易大学特大城市经济社会发展研究协同创新中心资助计划(2015TDCS013)；中国流通研究院资助计划(2015LTJJ013)

F270

A

1671-816X(2017)03-0024-08