风电机组Ⅱ区功率与叶片气动载荷协同控制*
2017-02-10王湘明任树平
王湘明, 任树平
(沈阳工业大学 信息科学与工程学院, 沈阳 110870)
风电机组Ⅱ区功率与叶片气动载荷协同控制*
王湘明, 任树平
(沈阳工业大学 信息科学与工程学院, 沈阳 110870)
为了研究风力发电机组在低于额定功率时的最大风能捕获以及叶片的气动载荷,使得风力发电机组在整个生命周期内高效稳定地运行,提出了一种功率与载荷的协同控制方法,通过过渡区预变桨的方式控制风力发电机组功率与叶片气动载荷.采用所提出的功率与载荷协同控制策略在Matlab软件上搭建风力发电机组的仿真模型,计算得出了风力发电机组的功率和叶片气动载荷的数据,结果显示,协同控制策略能够在低于额定风速区域保持功率基本不变的情况下有效减小叶片的气动载荷,由此证明了所提出的协同控制策略的可行性.
风力发电机组; 风功率; 最大功率追踪; 最佳叶尖速比; 叶片; 气动载荷; 协同控制; 柔性变桨
随着人类社会的不断发展,人类对化石燃料的消耗不仅导致了化石能源的迅速枯竭,同时因大量使用化石能源致使全球环境问题日益严重.面对不可生能源有限的问题,人们利用科学技术逐渐发展可再生能源.风能在很长一段时间内被人们利用,风力发电技术在近几年已经得到了广泛应用与推广,世界各国都在大力推进风力发电的步伐.风力发电机组的单机容量也在逐年递增,从原先的千瓦级已近扩充到兆瓦级,并且容量还在攀升,然而,风力发电机组作为一个复杂的、多变量、强耦合的非线性系统想要在获得最大风功率的同时减小风力发电机组叶片所受的载荷,这对风力发电机组的可靠性和使用寿命有严格要求[1-6].
传统的风力发电机组在额定风速以下运行时,为了获得更多的风能,一般采用定桨距的方式,运用最大风能捕获原理来达到最大功率输出.文献[7]中列举了目前常用的风力发电机组最大风能捕获的方法,但是没有提到在获取风能的同时对叶片气动载荷的控制;文献[8]中提出了一种涉及疲劳载荷的风功率追踪,却没有正真在后续仿真中提及叶片载荷;文献[9]中对叶片的载荷进行了详细分析及计算,但都是面向于额定风速以上及极限条件的载荷问题.本文主要针对传统变速变桨距风力发电机组在Ⅱ区时的最大功率获取以及叶片的载荷问题进行研究,提出了一种额定风速以下柔性变桨控制策略,改变了传统风力发电机组在额定风速以下依靠单一的调节电机功率来控制转速的方式,保证了在获取最大风功率的同时缓解叶片的瞬态载荷.应用Matlab仿真平台模拟风力发电机组,采用所提出的控制策略进行仿真分析,验证了本策略的有效性和真实性.
1 最大风能捕获
根据动能等效原理可知,风力发电机产生的机械功率为
(1)
式中:ρ为空气密度;S为风力机桨叶扫掠面积;Cp为风能利用系数,又称功率系数;v为风速.
在来流风速v已定的情况下,风力发电机组获得的输入机械功率只取决于风能利用系数Cp,而Cp又是叶尖速比λ和桨叶桨距角β的函数,具体表达式[10-11]为
(2)
叶尖速比λ是风轮叶尖的线速度与风速之比,即
(3)
式中:ω为风轮旋转的机械角速度;R为叶片半径.
结合式(1)和(2)可以看出,风力发电机组的功率与风能利用系数Cp、风速v的三次方以及风轮的扫轮面积成正比.
将风力发电机组叶尖速比和桨距角范围设定为[0,20]和[0°,20°],取叶尖速比λ和桨距角β每一步的步长为0.5,利用式(2)可得出理想风能利用系数Cp与叶尖速比λ以及桨距角β的关系如图1所示.
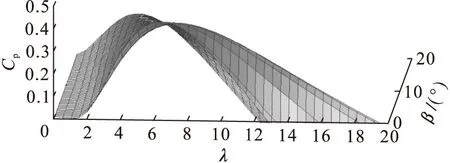
图1 理想风能利用系数与叶尖速比、桨距角关系曲线Fig.1 Curves of ideal wind power coefficient, tip speed ratio and pitch angle
从图1中可以看出,在不同叶尖速比及桨距角下的风能利用系数是不同的.当桨距角固定时,风力发电机组的风能利用系数和叶尖速比成抛物线关系,每一条曲线上都有一个最大风能利用系数.将图1中每条曲线对应的最大风能利用系数提出来制成表1.从表1中可以清楚看到,当风速v和桨距角β都固定在某一值时,则存在一个最佳叶尖速比λopt,使得风能利用系数Cp的值最大,也就是风力发电机组获得气动功率最大.根据表1中的数据可以看出,桨距角在0~20°之间变化时,风能利用系数所对应的叶尖速比λ主要在4~7.5之间变化.
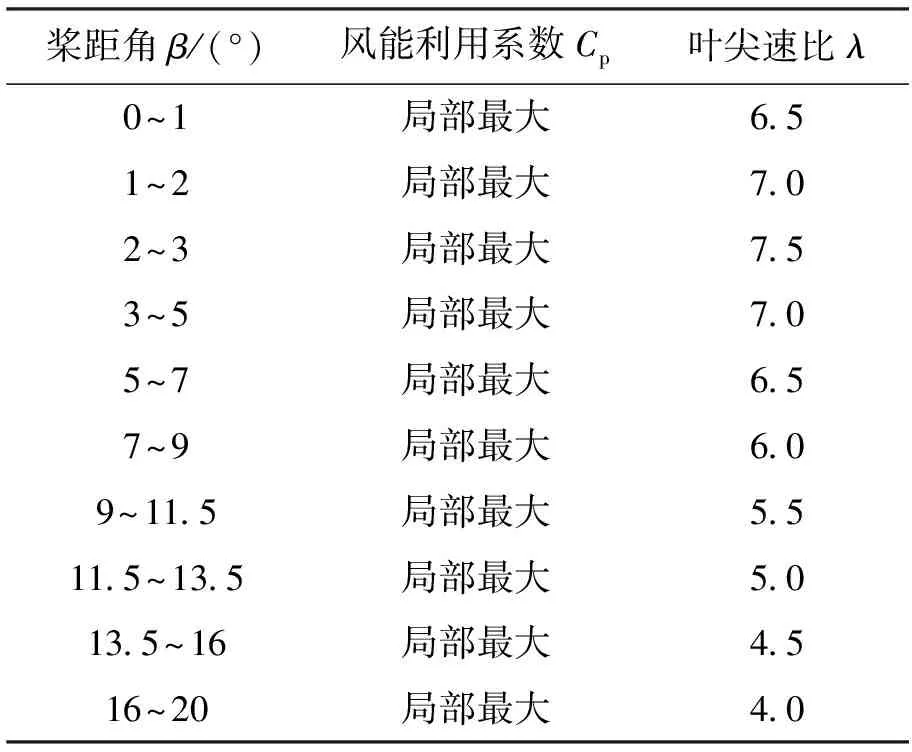
表1 最大风能利用系数对应的叶尖速比和桨距角Tab.1 Tip speed ratio and pitch angle corresponding to maximum wind power coefficient
采用最佳叶尖速比法作为风力发电机组低于额定风速时最大风功率捕获方法,依据给出的最佳叶尖速比,通过电机控制器调节风力发电机的转速来调节风轮转速,使风力发电机沿着图2所示的功率曲线Popt运行.图中的功率曲线依次代表的是风速从v1~v7变化的功率曲线,其中风速从v1到v7是一个逐渐增大的过程,且没有超出额定风速的范围[12].
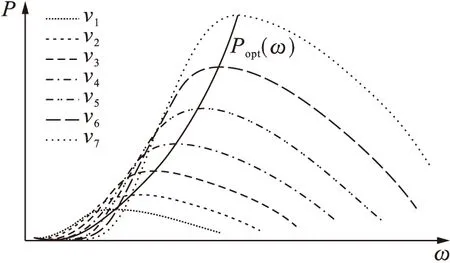
图2 最佳功率曲线追踪Fig.2 Optimal power curve tracking
2 叶片载荷
叶片的载荷是指叶片所受的力与力矩的总和.风力发电机组通过叶片转化风能,并将风能转化为机械能,它是风力发电机组中的重要组成部分.本文主要研究的是风力发电机组运行在Ⅱ区时的气动载荷情况,通过实验研究缓解该区叶片的气动载荷,延长使用寿命.文中将空气动力学的基本理论和计算方法用于建立叶片载荷计算模型,并结合变桨距控制基本理论研究叶片的气动载荷.常见的气动载荷主要包括:叶片的轴向力载荷、切向力载荷、摆振载荷及挥舞载荷[12-14],其表达式为
(4)
(5)
(6)
(7)
式中:Qxb为轴向剪力载荷;Qyb为切向剪力载荷;Mxb为绕主轴中心的转矩,即摆振载荷;Myb为叶片挥舞方向的弯矩,即挥舞载荷;ri为轮毂的半径;W为相对分速;c为叶片某一半径处的弦长;Cn为法向力系数;Ct为切向力系数.
在以上四个载荷的计算中,首先需要计算出合成风速,它是来流风速和风轮切向风速的合成.此外,还需要计算Cn、Ct,其中参数的具体计算参考文献[15]中的方法.
3 Ⅱ 区功率与叶片气动载荷的协同控制
风力发电机组在Ⅱ区的功率获取与控制一直是研究功率问题的一个关键环节,但是随着风电技术的不断发展,风电机组容量的不断扩大,对于长时间处于Ⅱ区的风力发电机组叶片来说会有非常大的损耗,因此,如何在Ⅱ区功率保证的情况下控制叶片的气动载荷至关重要.
3.1 传统变速变桨控制策略
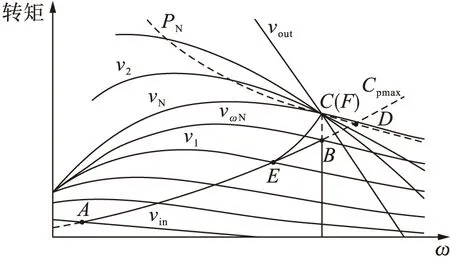
图3 变速变桨距风力发电机组控制策略Fig.3 Control strategy for wind turbine with variable speed and variable pitch
在低风速区,风力发电机组从切入风速为vin的A点到沿着最大功率曲线(Cpmax)一直运行到风速为vωN的B点,此区间称为最大功率追踪区.由于在B点发电机转速达到了其上限值ωN,当风速从vωN上升到vN时,转速将恒定在ωN,提升发电机电磁转矩使风力发电机组达到其额定功率.在图3中为BC段,此段也称为恒转速区,在该区间一般保持桨距角为零度不变.当风速超过额定风速vN时,变桨距系统将开始工作,通过改变桨距角保持风力发电机组功率的恒定,使风电机组持续运行在C点,直到风速超过切出风速vout,此区间称为恒功率区.在此需要注意的是:若最大功率PN曲线与Cpmax曲线的相交点在额定转速极限值左侧,就会造成风电机组在未达到额定转速时,已进入失速状态,相应的AB区间将被缩小,这时就需对整个风电机组额定点进行重新选取.
从图3可以看出,3个区间工作点的划分非常明显,在AB段一般保持桨距角不变,通过调节风力发电机的电磁转矩来控制叶尖速比,使风功率在某一抛物线上达到最大值;BC段通过增大风力发电机的电磁转矩来使风功率达到额定值;CD段通过改变桨距角来控制所获得功率以及保证机组的安全.
由于风力发电机组在整个生命周期中会有较长的时间处在额定功率以下的状态,当遇到风速剧烈波动时,风力发电机组不但会产生较大的功率变化,导致电网电压不稳定,同时也会在叶片上产生较强的瞬态载荷.低风速时由于固定桨距角不变,长时间处在这种状态下会增加机组叶片的疲劳载荷,增加维修成本,缩短机组的使用寿命.为了更好地控制气动转矩,减小疲劳载荷,保证机组安全,需要改进传统的控制策略.
3.2 改进控制策略
改进的变速变桨距控制策略结构框图如图4所示.
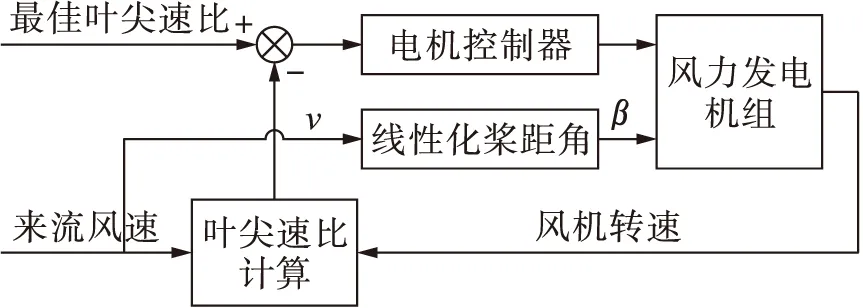
图4 改进的桨距角控制策略Fig.4 Improved control strategy for pitch angle
由图4可以看出,在桨距角控制中引入了风速,即对变桨控制系统做了一个线性化处理,当风速在较小的范围内变化时,可以根据实时风速对桨距角做一个微小调节,这个调节是无法通过电机功率反馈调节的;当风速变化范围较大时,依靠电机功率反馈来调节桨距角具有一定的滞后性,桨距角的变化不能跟随风速实时变化,加入线性化风速后,桨距角随风速变化会存在一个理论的匹配值,当风速不断变化时,可以根据桨距角的变化来调节风力发电机组的励磁状态,使得不同风速条件下获得最佳叶尖速比控制,保证风功率最大.此外,也可以在电机功率反馈的基础上依据风速变化实时调节桨距角变化,确保叶片在运转过程中的载荷冲击最小.通过叠加的桨距角控制可以更好地得到功率和载荷的变化,以达到功率与载荷协同控制的目的.改进后的变速变桨距控制策略如图3中曲线AEF所示,而在实际控制中,采用的是一个过渡区柔性变桨,变桨曲线如图5所示.
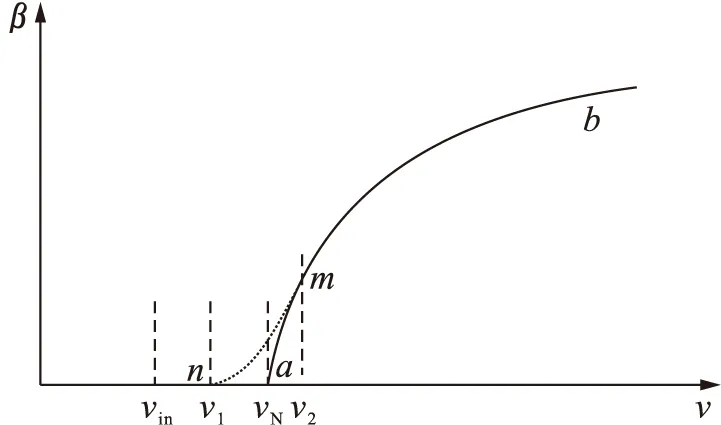
图5 改进的桨距角曲线Fig.5 Improved pitch angle curve
曲线amb为传统变桨方式,曲线nmb为改进变桨方式.改进策略与基本策略的最大区别之处在于:在风速未到达额定时,添加一个缓冲区,缓冲区出现的位置是以风速v1开始,风速v2结束,相应的桨距角控制方式也发生了改变.在低风速区,控制策略基本不变,叶片承受动态载荷较小,因此只需沿着最大功率系数Cp运行即可.但当风速达到v1时进入缓冲区,在缓冲区,转速将以更小的斜率随风速的增加而增加.为了提高工作点的控制力,桨距角也随着风速的增加而缓慢线性增加,当风速达到v2时,过渡区结束.由图5可以看出v1 本文研究对象为三叶片上风向变速变桨距风力发电机组,其主要技术参数如下:额定功率为200 kW,额定风速为12.5 m/s,风轮额定转速为48 rad/min,切入和切出风速分别为3.5 m/s和25 m/s,风轮直径为27.55 m.风速采用了随机函数按照1 s变化的随机风,最大风速12 m/s,最小风速3 m/s,随机风速仿真曲线如图6所示. 图6 随机风速仿真曲线Fig.6 Simulation curves at random wind speed 采用Matlab/Simulink模块搭建风力发电机组模型,对传统变桨距控制策略和改进的控制策略进行仿真.结合200 kW风力发电机组叶片的数据,采用Matlab编程对改进前后的叶片气动载荷进行仿真计算,仿真图如图7所示.(实线代表传统控制方式下功率和载荷曲线,虚线代表改进控制方式下的功率和载荷曲线.图8~11同.) 风速随时间瞬时变化过程中,风功率也随着变化,但是可以明显看出,改进后的风功率与改进之前相比略有减小,但基本维持不变.采用仿真图6中不断变化的风速,在Matlab软件中计算通叶片沿径向受到的气动载荷,具体结果如图8~11所示. 图7 改进前后的风功率仿真图Fig.7 Simulation of wind power before and after improvement 图8 改进前后叶片轴向剪力仿真图Fig.8 Simulation of axial shear of blades before and after improvement 图10 改进前后叶片轴向摆振载荷仿真图Fig.10 Simulation of axial shimmy load of blades before and after improvement 图11 改进前后叶片切向挥舞载荷仿真图Fig.11 Simulation of tangential wave load of blades before and after improvement 过仿真图可以清楚看到,图7中改进后的风力发电机组的风功率略有减小,采用算数求均差方法与传统方法进行对比,改进策略减小的风功率占改进前平均风功率的0.2%,这与风力发电机组功率略有减小相吻合;图8中作用在风力发电机组叶片上的轴向剪力与改进前相比有所减小,采用求均差方法计算得出轴向剪力减小的平均值为81.10 N,与改进前轴向剪力均值相比减小14.28%;图9中切向剪力减小的均差值为23.43 N,与改进前切向剪力均值相比减小21.02%;图10中摆振载荷与改进前相比也在减小,其中摆振载荷减小的均差值为40.38 N·m,与改进前摆振载荷均值相比减小8.79%;图11中挥舞载荷减小的均差值为233.84 N·m,与改进前切向挥舞载荷均值相比减小8.32%.实验结果与改进策略的结果保持一致,证明了控制策略的有效性. 本文从功率与载荷协同控制的角度出发,提了一种过渡区域桨距角控制策略,能够在额定风速以下实行柔性变桨,减小叶片瞬间载荷的同时保证额定风速以下功率基本不变.该方法可以消除风力发电机组在额定功率点附近运行时,由于瞬间变化所造成的功率波动及突变载荷等不利影响. 通过对所提出的风力发电机功率与载荷协同控制策略的仿真结果可以看出,改进后的控制策略能够很好地缓解叶片受气动力作用所产生的轴向力和摆振载荷,并且切向力和挥舞载荷变化幅度不大,同时也能基本保证风功率稳定不变,证明了方案的有效性和可行性. [1]Muyeen S M,Takah A,Mura T,et al.Avariable speed wind turbine control strategy to meet wind farm grid code requirements [J].IEEE Transon Power Systems,2010,25(1):331-340. [2]李慧兰.我国风电发展现状及其前景展望 [J].科学之友,2013(11):111-113. (LI Hui-lan.Present situation and prospect of wind development in China [J].Friend of Science Amateurs,2013(11):111-113.) [3]Lin W M,Hong C M.Intelligent approach to maxi-mum power point tracking control strategy for variable-speed wind turbine generation system [J].Energy,2010,35(6):2440-2447. [4]Luo C L,Banaka R H,Shen B K,et al.Strategies to smooth wind power fluctuations of wind turbine gene-rator [J].IEEE Transactions on Energy Conversion,2007,22(2):341-349. [5]田友飞,李啸骢,徐俊华.变速恒频双馈风电机组最大风能捕获非线性控制策略 [J].电力系统自动化,2011,35(11):27-33. (TIAN You-fei,LI Xiao-cong,XU Jun-hua.VSCF doubly fed wind turbine maximum wind energy capture nonlinear control strategy [J].Automation of Electric Power Systems,2011,35(11):27-33.) [6]李阳,李华强,肖先勇.风特性对风力发电机组输出功率的影响 [J].可再生能源,2012,30(5):34-38. (LI Yang,LI Hua-qiang,XIAO Xian-yong.The impact of wind characteristic on the wind turbine generator [J].Renewable Energy Resources,2012,30(5):34-38.) [7]程尹曼,汪明媚,王映斐.风力发电系统中最大功率点跟踪方法综 [J].华东电力,2010,38(8):1393-1398. (CHEN Yin-man,WANG Ming-mei,WANG Ying-fei.Methods of maximum power point tracking of wind energy conversion system [J].East China Electric Power,2010,38(8):1393-1398.) [8]刘军,何玉林,李俊.变速变桨距风力发电机组控制策略改进与仿真 [J].电力系统自动化,2011,35(5):82-86. (LIU Jun,HE Yu-lin,LI Jun.Variable speed wind turbine pitch control strategies improvement and simulation [J].Automation of Electric Power Systems,2011,35(5):82-86.) [9]Deng Y,Jiang Y J.Extreme loads calculate and secu-rity analysis of wind turbine variable pitch actuator [C]//IEEE Renewable Power Generation Conference.Beijing,China,2013:1-5. [10]马卫东.风力发电机组最大功率追踪 [J].高压电器,2012,48(7):58-61. (MA Wei-dong.Wind turbine maximum power point tracking [J].High Voltage Apparatus,2012,48(7):58-61.) [11]张凤,阎秀恪,兰宏光,等.基于滑模控制的风机最大风能追踪 [J].沈阳工业大学学报,2014,36(6):625-630. (ZHANG Feng,YAN Xiu-ke,LAN Hong-guang,et al.Maximum power point tracking of wind turbine based on sliding model control [J].Journal of Shen-yang University of Technology,2014,36(6):625-630.) [12]Tsai M F,Tseng C S,Hung Y H.A novel MPPT control design for wind-turbine generation systems using neural network compensator [C]//IEEE IECON 38th Annual Conference.Montreal,Canada,2012:3521-3526. [13]张少帅,王章琦.风力发电机气动载荷分析和独立变桨控制技术研究 [D].保定:华北电力大学,2013. (ZHANG Shao-shuai,WANG Zhang-qi.Wind turbine aerodynamic load analysis and independent variable propeller control technology research [D].Baoding:North China Electric Power University,2013.) [14]高龙,王维庆.水平轴风力发电机叶片的载荷计算与模态分析 [D].乌鲁木齐:新疆大学,2014. (GAO Long,WANG Wei-qing.Horizontal axis wind turbine blade load calculation and the model analysis [D].Urumchi:Xinjiang University,2014.) [15]Martin O L,Hansen M.Aerodynamics of wind turbines [M].London:Earthscan,2008:2-65. (责任编辑:景 勇 英文审校:尹淑英) Cooperative control for Ⅱdistrict power of wind turbine and aerodynamic load of blades WANG Xiang-ming, REN Shu-ping (School of Information Science and Engineering, Shenyang University of Technology, Shenyang 110870, China) In order to study the maximum wind power capture of wind turbine and the aerodynamic load of blades below the rated power and make the wind turbine run efficiently and stably in whole life cycle, a cooperative control method for both power and load was proposed. Through adopting the pre-pitch strategy in the transition zone, the aerodynamic load of blades and the power of wind turbine were controlled. Through adopting the proposed power and load cooperative strategy, a simulation model for the wind turbine was established with Matlab software, and the data for the power of wind turbine and the aerodynamic load of blades were calculated. The results show that the cooperative control strategy can effectively reduce the aerodynamic load of blades under the condition of keeping the power basically unchanged in the districts below the rated power. Therefore, the feasibility of the proposed cooperative control strategy is proved. wind turbine; wind power; maximum power tracking; optimal tip speed ratio; blade; aerodynamic load; cooperative control; flexible pitch 2016-01-06. 科技型中小企业技术创新基金资助项目(13C26212101002). 王湘明(1963-),男,湖南宁乡人,副教授,硕士,主要从事风力发电控制技术、电机控制等方面的研究. 14∶01在中国知网优先数字出版. http:∥www.cnki.net/kcms/detail/21.1189.T.20160512.1401.034.html 10.7688/j.issn.1000-1646.2017.01.02 TM 315 A 1000-1646(2017)01-0006-064 协同控制仿真及其结果分析
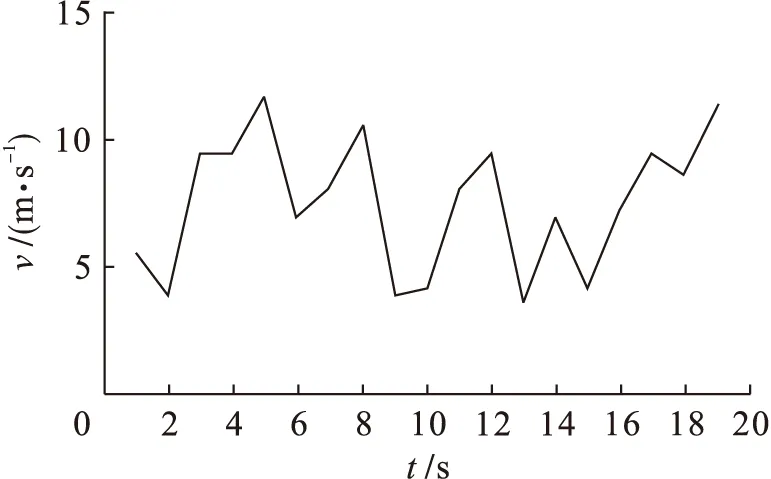
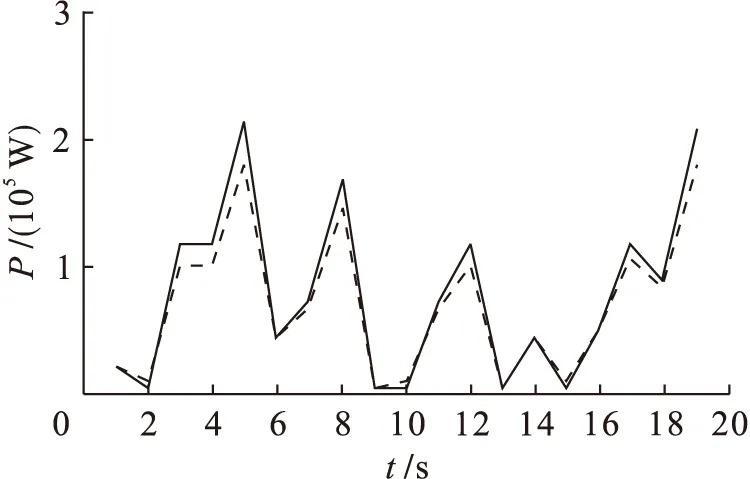
5 结 论
