公差分析在航空发动机设计中的应用研究

2017-02-10陈渊博单福平

制造业自动化 2017年1期

关键词：形位方根公差

陈渊博，单福平

（中国航发商用航空发动机有限责任公司，上海 201108）

公差分析在航空发动机设计中的应用研究

陈渊博，单福平

（中国航发商用航空发动机有限责任公司，上海 201108）

简要介绍了公差传递模型及求解方法，针对航空发动机整机尺寸链设计特点，详细介绍了某型发动机典型径向跳动、径向及轴向间隙分析过程及结果。通过考虑尺寸公差、形位公差、周向定位三种不同维度比较对结果的影响，同时详细分析了三种公差求解方法的应用特点。

公差设计；尺寸及形位公差；极值法；均方根法；蒙特卡洛法

0 引言

航空发动机零组件数量众多、结构复杂，整机关键装配尺寸（如叶尖间隙、转静子同轴等）对产品性能和可靠性有重要影响。公差分析是研究机械产品中尺寸及公差之间的相互关系，分析影响装配精度的因素，决定各零件尺寸和位置的适宜的公差，从而求得保证产品装配精度与技术要求的经济合理的方法。

国内航空发动机领域，目前发动机的公差设计多以经验为主，需要反复的试凑以达到要求；而公差分析仍以传统的一维尺寸链为主，即只计算尺寸公差形成的尺寸链，难以有效处理特征上的方向和形状等形位公差。行业内已经开始尝试二维以及三维公差分析方法，考虑形位公差的影响，采用概率统计方法进行公差设计[1]。

本文详细介绍了不同的公差分析方法在航空发动机尺寸链设计中的应用特点。

1 公差分析方法介绍

1.1 典型的公差传递建模方法

公差传递模型也称为公差传递函数，它是进行公差分析的理论基础。公差传递函数是尺寸链中欲求解的封闭环与已知的组成环之间函数关系的表达式[1]，设公差函数为：

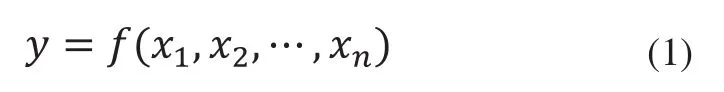
式中，y为欲求解的封闭环的尺寸及偏差；n为已知组成环的个数；x1,x2,…,xn为相互独立的已知的组成环的尺寸及偏差。

1.2 典型的公差传递模型求解方法

不同的公差设计方法其公差传递函数不同，基于零组件在装配时公差值的处理方式不同，根据公差传递函数是否为线性以及各零组件已知尺寸公差的分布特性，可以把公差传递模型的求解方法统分为极值法和统计分析法。常见的统计分析方法有均方根法、蒙特卡洛法等[2]。

1.2.1 极值法

使用极值法计算封闭环的公差，主要适用于：封闭环精度要求较高的话，尺寸链环数就要少；尺寸链环数较多的话，封闭环精度就得要求低些，即极值法适用于组成环平均公差较大的尺寸链。

1.2.2 均方根法

均方根法也叫概率法，它是以一定置信水平为依据，通常封闭环趋近正态分布，取置信水平P=99.73%。因此，按均方根法计算公差，不要求100%互换，只要求大数互换。对于某些重要场合，应当有适当的工艺措施，排除可能有0.27%产品超出公差范围或极限偏差[3]。取置信水平P=99.73%时，封闭环相对分布系数为l。

均方根法适用于封闭环精度高、组成环环数较多的尺寸链。应用均方根法有可能使各组成环获得较为宽松的公差量。

1.2.3 蒙特卡洛法

“蒙特卡洛法”亦称为随机模拟（Random simulation）方法或随机抽样（Random sampling）方法。该方法的基本思想是，为了求解数学、物理、工程技术以及生产管理等方面的问题，首先建立一个概念模型或随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，最后给出所求解的近似值，解的精确度可用估计值的标准误差来表示。蒙特卡洛法的基本原理，是利用各种不同分布随机变量的抽样序列模拟实际系统的概率统计模拟模型，给出问题数值解的渐近统计估计值[4,5]。

用蒙特卡洛法进行公差分析的步骤如下：

1）明确各组成环尺寸的分布规律；

2）根据计算精度的要求确定随机模拟次数N；

3）根据各组成环尺寸的分布规律和分布范围，分别对其进行随机抽样，从而得到一组组成环尺寸的随机数(Al,A2,…,An)；

4）将随机抽样得到的一组各组成环尺寸的随机数(Al,A2,…,An)代入尺寸链方程，计算封闭环尺寸A0，得到该尺寸的一个子样；

5）将上述步骤3）、4）重复N次，即可得到封闭环尺寸的N个子样，构成一个样本；

6）对所得到的封闭环尺寸的样本进行统计处理，从而确定封闭环尺寸的平均值、极限值、公差等。

2 公差分析模型

本文的研究对象为典型双转子涡扇航空发动机，其转子件多为盘、鼓筒轴类，采用轴对称设计，使用短圆柱止口定心及端面定位；静子件多为薄壁机匣，也是采用短圆柱止口定心及端面定位。由于航空发动机制造精度和装配精度要求都很高，其中尺寸公差、形位公差和装配工艺均会对最终的装配质量产生较大影响。基于尺寸链的公差传递模型无法完全考虑这些因素，因此采用三种分析方案来对比说明：方案一是只定义尺寸公差的模型，方案二是定义尺寸公差和形位公差的模型，方案三是定义尺寸公差、形位公差和周向螺栓分布（引入周向基准）的模型。

不同的公差传递模型和求解方法各有优缺点，为了说明不同公差分析方法在航空发动机中的适用性，本文以某型双转子涡扇航空发动机为例，对发动机中典型的三种测量（径向跳动、径向间隙、轴向间隙）分别选取了一个例子进行分析。

径向跳动测量选取高压压气机七级盘盘心相对于高压前轴颈柱面和高涡后轴柱面联合基准的跳动，如图1所示；径向间隙测量选取高压压气机封严篦齿盘与前置扩压器进口的径向间隙，如图3中的7号所示；轴向间隙测量选取高压涡轮一级导向器组件与高压涡轮一级工作叶片的轴向距离，如图3中的5号所示。

3 公差分析方法对比

3.1 公差传递模型对比

本小节采用三个例子针对不同的公差传递模型进行对比分析，为保证变量的唯一性，选用模型及输入条件一致，在同一款商用偏差分析软件中进行对比分析。公差传递模型的三种分析方案分别如1）、2）、3）所述。

3.1.1 针对径向跳动测量分析

航空发动机高、低压转子通过各自的轴承支撑到承力框架上，在尺寸链分析过程中，高、低压转子可以相互独立。以图1中径向跳动测量为例进行建模分析，测量方案采用基准端夹紧（模拟前后轴承支撑），测量端采用八个点到线的测量方式，近似用点到中心线的最大、最小距离之差来模拟全跳动。零组件尺寸及形位公差以研制阶段公差精度数值为输入，采用正态分布模型，装配关系定义参考实际装配工艺。

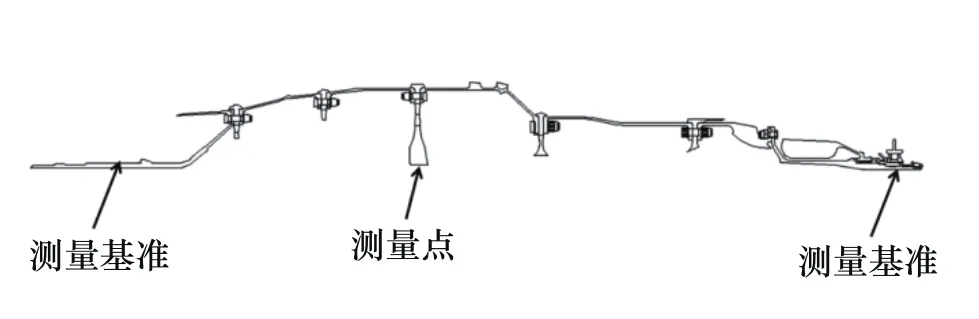
图1 径向跳动测量

1）当仅存在尺寸公差时，七级盘盘心对前后联合基准的径向跳动并不存在。

这是因为七级盘上均布的八个测点都仅有沿径向的平移，它们是受到各级零件径向尺寸公差的约束，而并不存在偏转，如图2所示。当测点随着各级零件在直径公差范围内波动时，各点平移量相同，点到中心线的距离矢量和为零。因此，跳动为零，即该约束条件下不存在盘心跳动。

图2 测点径向移动

2）当增加形位公差后，求得盘心波动均值为0.061mm，标准偏差为0.029mm。设定跳动量合格区间为（0，0.05），则合格率为39.8%（发动机研制阶段合格区间尚未定论，计算合格率可能偏低，本文只比较相对合格率）。形位公差对测量结果起到关键影响。贡献率排前七的影响因素都是端面形位公差，包括端面跳动、端面平行度等。各端面之间通过彼此配合来传递公差，一个面如果有微小的偏转，通过零件远距离的杠杆效应，传递到测量端都会造成极大的偏转。

3）在方案二的基础上，利用精密螺栓进一步增加周向定位约束条件，求得盘心波动均值为0.062mm，标准偏差为0.029mm。设定跳动量合格区间为（0，0.05），则合格率为40%。方案3与方案2的结果近似，仍然说明了形位公差对测量结果起到关键影响。贡献率排前七的影响因素仍都是端面形位公差，包括端面跳动、端面平行度等，而增加的螺栓定位并没有明显改变测量结果。

3.1.2 针对径向间隙测量分析

以图3中7号测量（高压压气机封严篦齿盘与前置扩压器进口的径向间隙）为例进行建模分析，测量方案采用轴孔配合模式下的虚拟间隙来求解径向间隙，其他参数定义与上一节一致。

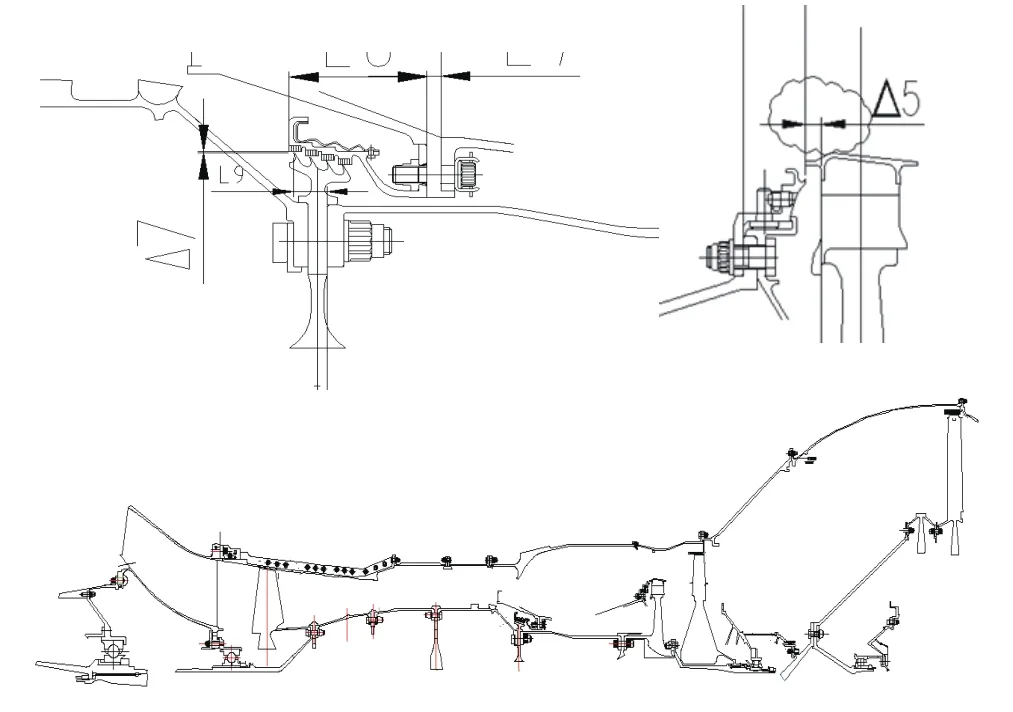
图3 间隙测量要求

1）当仅存在尺寸公差时，求得7号径向间隙的均值为0.513mm，标准偏差为0.017mm。设定间隙量合格区间为（0.47，0.53），则合格率为82.2%。在没有形位公差的情况下，7号径向间隙主要受到测量端孔、轴特征的尺寸公差的影响，以及燃烧室外机匣、高压压气机前后静子、高压涡轮前篦齿盘、高压涡轮鼓筒轴等浮动装配形式的影响。

2）当增加形位公差后，求得7号径向间隙的均值为0.493mm，标准偏差为0.026mm。设定间隙量合格区间为（0.47，0.53），则合格率为73.4%。与前一约束模型相比，此处装配间隙合格率明显降低，表明形位公差对装配质量有较大影响。同时，相比较前一约束模型，各影响因素贡献率发生了明显变化。7号径向间隙不仅受到测量端孔、轴特征的尺寸公差的影响、孔轴浮动装配形式的影响，形位公差对测量结果更是起到重要影响。形位公差通过零件远距离的杠杆效应，使测量端相对位姿发生极大改变。

3）在方案二的基础上，利用精密螺栓进一步增加周向定位约束条件，求得7号径向间隙的均值为0.491mm，标准偏差为0.027mm。设定间隙量合格区间为（0.47，0.53），则合格率为74.7%。方案3与方案2的结果近似，仍然说明了形位公差对测量结果起到重要影响，而增加的螺栓定位并没有明显改变测量结果。

3.1.3 针对轴向间隙测量分析

以图3中5号测量（高压涡轮一级导向器组件与高压涡轮一级工作叶片的轴向距离）为例进行建模分析，测量方案采用均布的四个测点到平面的距离来表示，需要观测轴向间隙的最小距离，其他参数定义参见上一节。

1）当仅存在尺寸公差时，求得5号轴向间隙的均值为6.140mm，标准偏差为0.065mm。设定间隙量合格区间为（6.105，6.165），则合格率为34.2%。在没有形位公差的情况下，5号轴向间隙主要受到端面线性公差的影响，而孔轴浮动装配形式则对结果影响甚微。

2）当增加形位公差后，求得5号轴向间隙的均值为6.115mm，标准偏差为0.070mm。设定间隙量合格区间为（6.105，6.165），则合格率为31.2%。与前一约束模型相比，此处装配间隙合格率有一定程度降低，此时形位公差影响作用并不明显。相比较前一约束模型，各影响因素贡献率并未发生明显变化。5号轴向间隙仍主要受到端面线性公差的影响，而浮动装配形式、形位公差因素对装配结果影响甚微，原因是止口装配和形位公差引起的零件偏心主要在径向上。

3）在方案二的基础上，利用精密螺栓进一步增加周向定位约束条件，求得5号轴向间隙的均值为6.110mm，标准偏差为0.074mm。设定间隙量合格区间为（6.105，6.165），则合格率为28.8%。可以看到，方案三相比较方案一、方案二来说，装配间隙合格率进一步降低。除了高压涡轮外机匣前端止口特征贡献率有所增加外，其他影响因素贡献率并未发生明显变化，增加的螺栓定位并没有明显改变测量结果。

3.1.4 小结

综合以上结果，对比如表1所示。

表1 模型对比计算结果

从表1可以看出，形位公差对径向跳动、径向间隙测量的结果有较大影响。形位公差通过多级零件远距离的杠杆效应，使测量结果变差。而对于轴向间隙测量，结果显示形位公差的影响并不显著，原因是形位公差在轴向并没有杠杆效应。

精密螺栓定位对于三类测量均没有明显影响。说明了在刚性体装配的建模环境下，对于以轴孔配合为主、大端面短柱面的回转体装配，圆周方向约束与否对径向跳动、径向间隙、轴向间隙测量结果并无太大影响。

以上分析说明针对航空发动机的特点，采用含有尺寸公差和形位公差的模型已经能够达到较高的尺寸链分析精度。

3.2 求解方法对比

本小节采用与上一小节相同的三个例子对极值法、均方根法和蒙特卡洛法进行对比分析。公差传递模型采用上一小节中含有尺寸公差和形位公差的模型。

3.2.1 针对径向跳动测量分析

以图1中径向跳动测量为例进行建模分析，建模方案如3.1.1节所述。

1）极值法

当所有公差位于极限值时，求得径向跳动的均值为0.152mm，标准偏差为0.073mm。设定跳动量合格区间为（0，0.05），则合格率为5.2%。

2）均方根法

当运用二维尺寸链模型进行均方根法计算时，公差传递路径如图4所示。

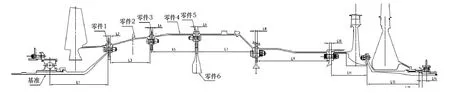
图4 径向跳动二维尺寸链模型

输入参数如表2所示。

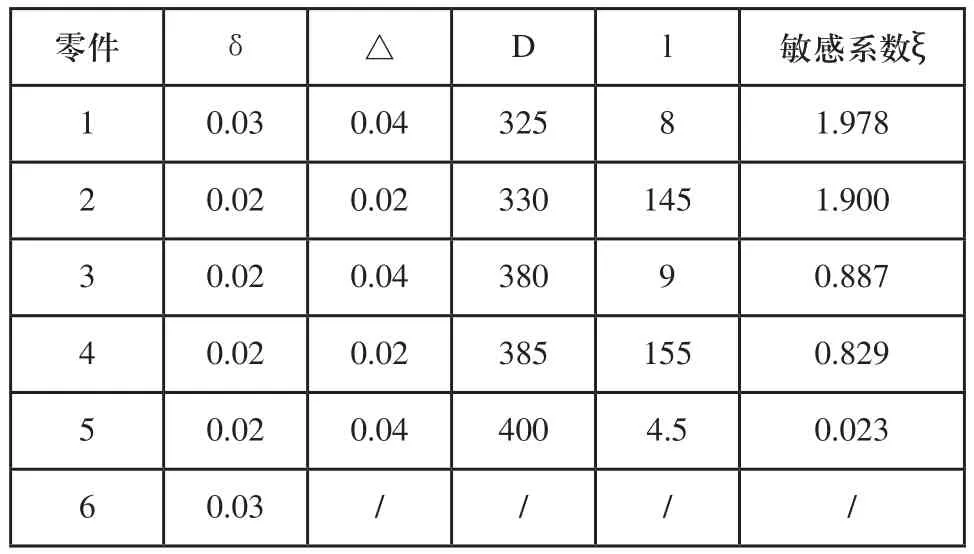
表2 径向跳动参数

表2中，表示径向跳动量，△表示轴向偏转距离，D表示零件直径，l表示零件长度，为敏感系数，通过直径与长度的关系式可计算得出[6]。

由以上结果可得公差传递函数为：

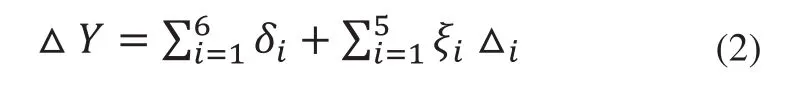
根据均方根法计算公式：

求得波动范围是：

根据计算结果，△Y服从N（0,0.0192）的正态分布，合格区间设置为（0,0.05），查正态分布表得到合格率为：49.62%。

3）蒙特卡洛模拟法

在偏差分析软件中采用蒙特卡洛模拟法时，求得盘心波动均值为0.061mm，标准偏差为0.029mm。设定跳动量合格区间为（0，0.05），则合格率为39.8%。

3.2.2 针对径向间隙测量分析

以图3中7号测量为例进行建模分析，建模方案如3.1.2节所述。

1）极值法

当所有公差位于极限值时，求得7号径向间隙的均值为0.424mm，标准偏差为0.066mm。设定间隙量合格区间为（0.47，0.53），则合格率为24.9%。

2）均方根法

当运用二维尺寸链模型进行均方根法计算时，公差传递路径如图5所示。

图5 径向间隙二维尺寸链模型

输入参数如表3所示。

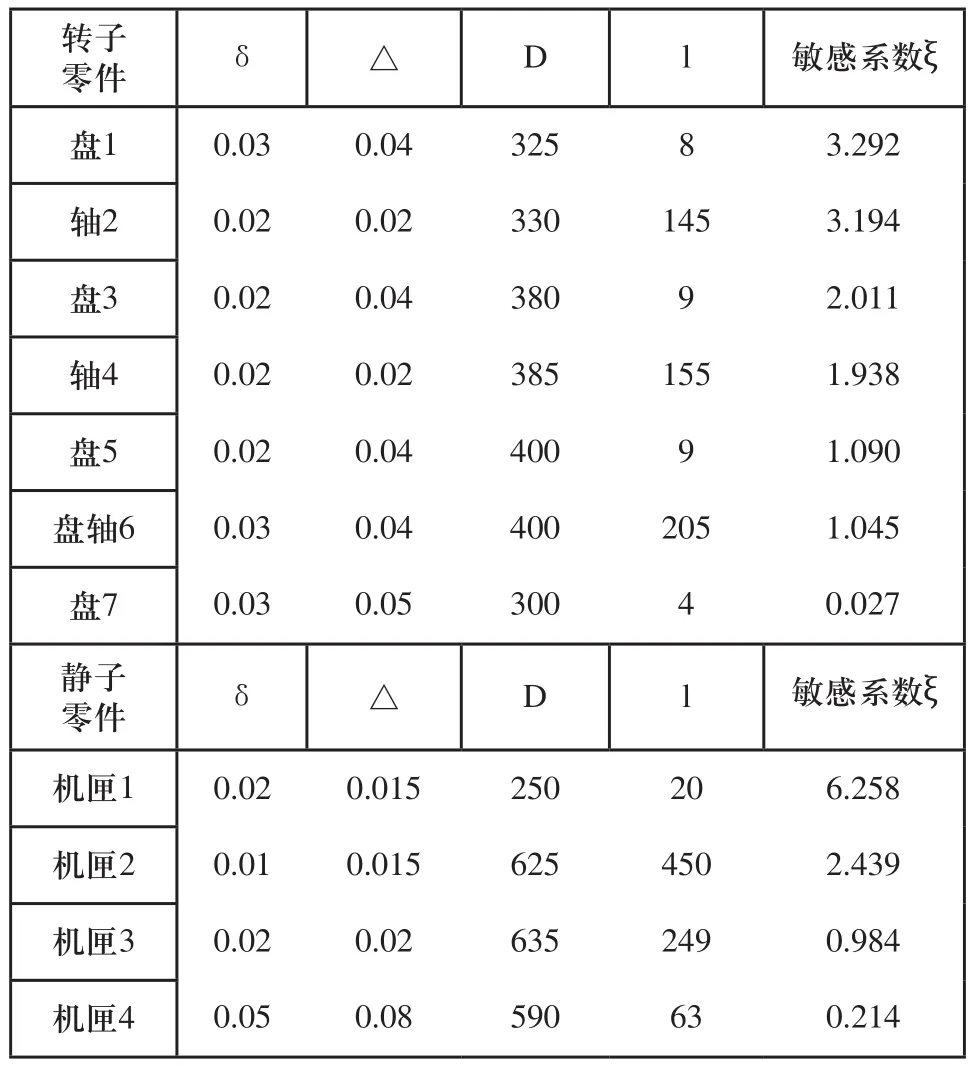
表3 径向间隙参数

由以上结果可得公差传递函数：

转子链：

静子链：

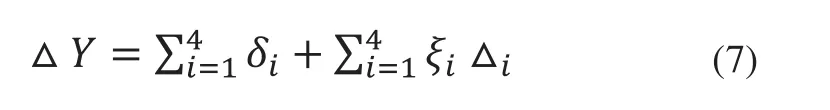
根据均方根法计算公式：

转子链：

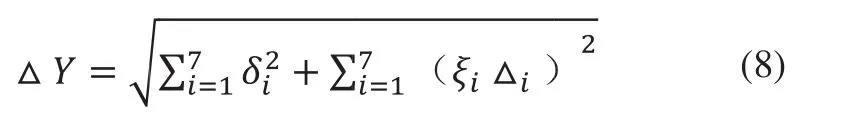
静子链：

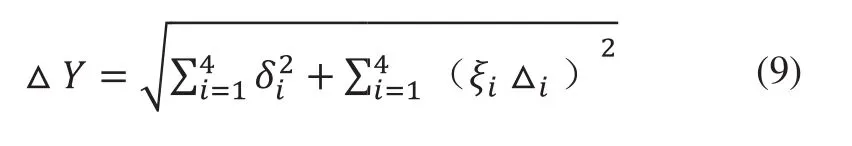
求得波动范围是：

根据计算结果△Y～N（0.5，0.0382），合格区间设置为（0.47，0.53），查正态分布表得到合格率为：57.04%。

3）蒙特卡洛模拟法

在偏差分析软件中采用蒙特卡洛模拟法时，求得7号径向间隙的均值为0.493mm，标准偏差为0.026mm。设定间隙量合格区间为（0.47，0.53），则合格率为73.4%。

3.2.3 针对轴向间隙测量分析

以图3中5号测量为例进行建模分析，建模方案如3.1.3节所述。

1）极值法

当所有公差位于极限值时，求得5号轴向间隙的均值为6.083mm，标准偏差为0.211mm。设定间隙量合格区间为（6.105，6.165），则合格率为10.3%。

2）均方根法

当运用二维尺寸链进行均方根法计算时，公差传递路径如图6所示。

输入参数如表4所示。

图6 轴向间隙二维尺寸链模型

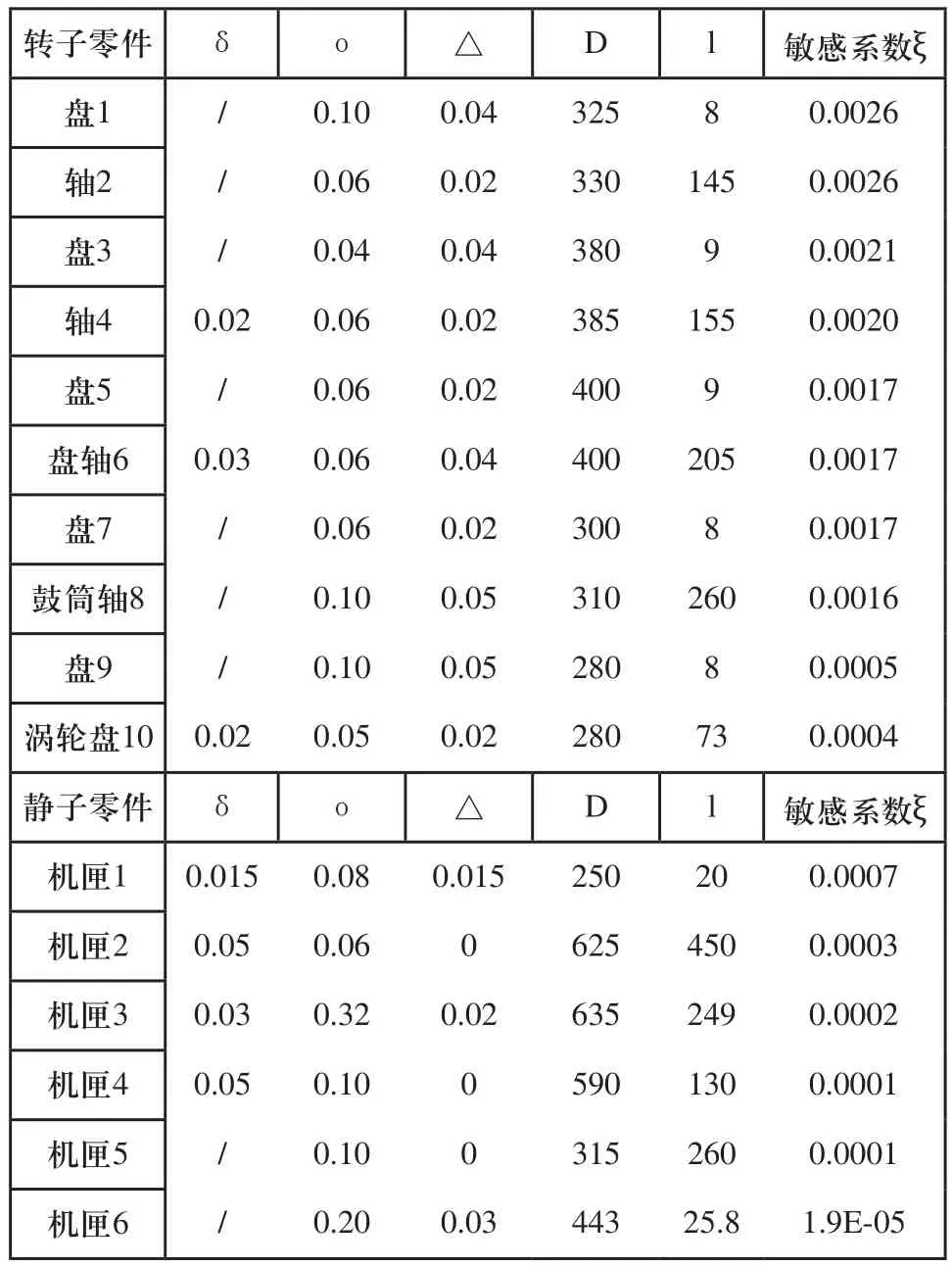
表4 轴向间隙参数

表4中，ο表示轴向尺寸公差。

由以上结果可得公差传递函数：

转子链：

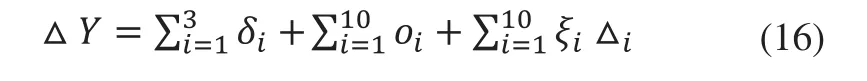
静子链：

根据均方根法计算公式：

转子链：

静子链：

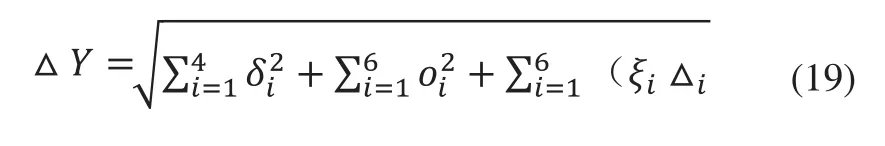
求得波动范围是：

根据计算结果△Y～N（6.135，0.0802），合格区间设置为（6.105，6.165），查正态分布表得到合格率为：29.23%。

3）蒙特卡洛模拟法

在偏差分析软件中采用蒙特卡洛模拟法时，求得5号轴向间隙的均值为6.115mm，标准偏差为0.070mm。设定间隙量合格区间为（6.105，6.165），则合格率为31.2%。

3.2.4 小结

综合以上结果，对比如表5所示。

表5 求解方法对比计算结果

从表中可以看出，运用极值法计算得到的装配偏差明显大于均方根法和蒙特卡洛模拟法。这也印证了传统的以极值法作为公差传递模型的求解方法往往会导致组成环公差要求过严，将会大大增加制造成本。

均方根法与蒙特卡洛法的计算结果理论上应该相近，但由于两者的公差传递模型并非完全一致，且手工建立模型的过程中进行了相应的简化，因此结果存在一定的差异。

与传统的极值法和均方根法相比，蒙特卡洛法在解决三维尺寸设计方面具有一定的优越性。该法在进行公差分析时，把求解封闭环尺寸及其公差的问题，当作求一个随机变量的统计量的问题来处理。由于尺寸链中各组成环的尺寸是在产品零件加工过程中得到的，其数值是在其公差范围内并符合一定分布规律的随机变量。尺寸链方程决定的封闭环尺寸，则是一组组成环尺寸的随机变量的函数，所以它也是一个随机变量。因此封闭环尺寸及其公差的确定，完全可以采用随机模拟和统计试验的方法，在一定条件下，用这种方法得到的结果，比较符合实际情况。