时间跨度对GPS坐标时间序列噪声模型估计影响分析

马梦然, 贺小星，2,花向红,3,4,舒 颖,龚果栋

(1.武汉大学 测绘学院，湖北 武汉 430079；2.华东交通大学 土木建筑学院，江西 南昌 330013；3.武汉大学 灾害监测与防治研究中心，湖北 武汉 430079；4.地球空间信息技术协同创新中心，湖北 武汉 430079)

时间跨度对GPS坐标时间序列噪声模型估计影响分析

马梦然1, 贺小星1，2,花向红1,3,4,舒 颖1,龚果栋1

(1.武汉大学 测绘学院，湖北 武汉 430079；2.华东交通大学 土木建筑学院，江西 南昌 330013；3.武汉大学 灾害监测与防治研究中心，湖北 武汉 430079；4.地球空间信息技术协同创新中心，湖北 武汉 430079)

文中介绍GPS坐标时间序列模型，并给出GPS噪声模型种类、估计方法及最佳噪声模型评价准则。选取来自IGS08的24个IGS核心站的时间序列作为数据基础，对不同时间跨度的时间序列噪声模型进行定量分析，探讨其随着时间变化的演化规律。结果表明：当时间序列长度较短时，噪声模型的不确定性较大，而12.5 a以上时间跨度的噪声模型趋于稳定且主要表现为闪烁噪声加白噪声的组合噪声模型；大跨度时间序列中噪声的长周期分量变得显著。

GPS坐标时间序列；时间跨度；噪声模型估计；影响分析

全球GPS连续观测站积累了大量的GPS观测数据，为高精度地球动力学研究提供了丰富的数据资料，也为分析GPS时间序列所包含的噪声信息提供了一个重要的基础。目前国内外学者已对GPS站坐标时间序列的噪声模型进行了大量研究，其中包括不同跨度对噪声模型的影响[1-3]。然而当前对GPS坐标时间序列噪声模型方面的研究仍存在一定的局限性：对噪声模型进行估计时，大部分研究所采用的时间跨度相对较短，使得噪声模型估计结果存在一定的不确定性；随着大尺度GPS时间序列的累积，传统方法中“闪烁噪声加白噪声”、“闪烁噪声、白噪声加随机游走噪声”为最佳噪声模型的假设是否符合实际；噪声模型估计、评价准则存在局限性等。为此，本文对5个不同时间跨度的时间序列数据进行分析，深入探讨时间序列跨度对噪声模型估计的影响，通过分析噪声模型的演化规律，探讨GPS基准站各噪声分量的最优噪声模型。

1 GPS噪声模型估计及评价准则

1.1 GPS噪声模型估计

已有的研究表明，GPS单站、单分量坐标时间序列y(ti)，通常满足模型(Nikolaidis, 2002)。即

(1)

式中:ti(i=1,…,n)为GPS站点单日历元，以年为单位，a表示站点位置(为序列的平均值)，b表示线速度，c，d和e，f分别为年周期和半年周期项的系数，g表示发生在历元Tg处的由于各种原因引起的阶跃(或称偏移)，H表示Heaviside阶梯函数，假定发生偏移的时刻Tg已知，τi为粘滞系数。

根据目前的研究，GPS时间序列中的噪声不仅包含白噪声，还包含有色噪声(闪烁噪声、功率谱噪声、随机游走噪声等)，并指出最优噪声模型为白噪声与有色噪声的组合模型[4-6]。对于不同噪声模型组合的协方差矩阵如下：

白噪声

(2)

白噪声和闪烁噪声

(3)

白噪声和功率谱噪声

(4)

白噪声、闪烁噪声和随机游走噪声

(5)

式(2)、(3)、(4)、(5)中：a为白噪声振幅；I为单位矩阵；b(bFL,bRW,bPL) 为有色噪声的振幅；J(JFL,JRW,JPL) 表示有色噪声的协方差矩阵。

1.2 最佳噪声模型评价准则

传统的对噪声模型进行评估的方法主要有功率谱分析法和极大似然估计法[7-10]。功率谱分析法可以对噪声模型进行定性估计，但其对低频噪声的分辨率较低，不能准确估计出低频噪声分量。针对功率谱分析的局限性，提出了极大似然估计的噪声估计方法。根据极大似然估计原理，不同噪声组合模型会得到不同的极大似然对数值(MLE)，数值越大结果越可靠。然而经典的MLE存在一个缺陷：噪声模型包含的未知参数越多，其MLE值也随之越大。此时简单选择MLE值较大的模型作为最优噪声模型不能确保结果的可靠性。Langbein (2008)提出了一种保守估计准则判断不同模型的优劣，通过设定经验值进行零假设分析，确定最佳模型。但这种方法受经验值的影响较大，有待进一步研究[1,4]。

综合分析以上模型评价方法，最终本文采用的方法为赤池信息量(Akaike information criterion，AIC)和贝叶斯信息量(Bayesian Information Criteria，BIC)的方法[11-12]。通过AIC/BIC的值评价不同模型的优劣，最终确定最佳模型，其基本原理如下：

AIC=-2ln(L)+2k,

(6)

BIC=-2·lnL+k·ln(n).

(7)

式中：L为某一模型下的似然函数(likelihood)，k为所拟合模型中参数的数量，n为观测值数目。根据AIC/BIC准则，似然函数L越大，对应的模型越好，此时对应最小的AIC/BIC值。对于大多数情况下AIC/BIC的值基本一致，对于一些特殊情况，AIC、BIC的结果并不完全一致时，由于BIC是根据一系列模型寻找的真实模型，建议选择BIC较小的作为最佳模型。

2 时间序列跨度影响分析

为了分析不同时间跨度对噪声模型的影响，本文综合考虑选择了时间跨度在18 a以上的连续观测值，且数据缺失率小于5% 的24个IGS08核心站的数据进行分析。站点分布见图1。其中，COCO测站位于地震活跃区域，可能受地震影响，使得其噪声模型存在不确定性。

本文选取了闪烁噪声加随机游走噪声(FN+RW)、闪烁噪声、随机游走噪声及白噪声(FN+RW+WN)、闪烁噪声加白噪声(FN+WN)、高斯马尔科夫噪声模型(GGM)、功率谱噪声模型(Power-law/PL)共5个噪声模型，利用极大似然估计噪声模型软件Hector[13-14]，对时间跨度为5 a、10 a、12.5 a、15 a和 20(18.10～20.02) a 5个时段的时间序列进行噪声分析。

2.1 不同时间跨度下不同噪声模型空间分布分析

通过统计不同跨度时间序列的AIC/BIC最小值，确定三坐标分量的最优模型。表1、表2、表3给出了不同时间跨度下不同噪声模型空间分布。

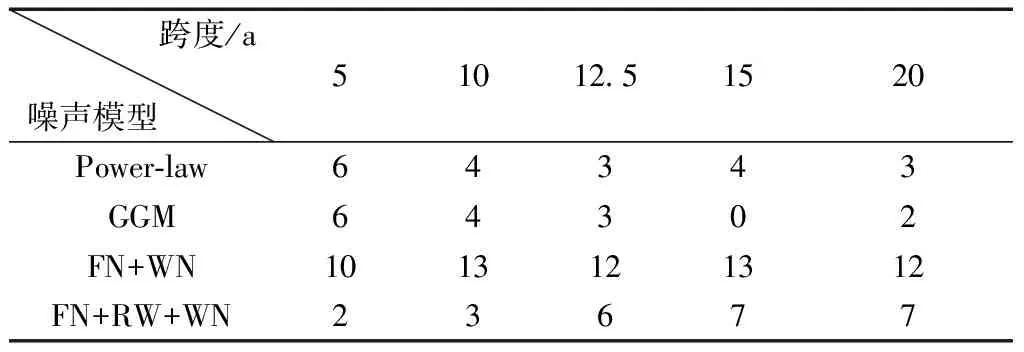
表1 不同时间跨度下不同噪声模型空间分布(N方向) 站数

图1 GPS时间序列跨度对噪声模型影响的站点分布

表2 不同时间跨度下不同噪声模型空间分布(E方向) 站数

表3 不同时间跨度下不同噪声模型空间分布(U方向) 站数

由表1～表3可知：N方向、E方向、U方向3个分量的最佳噪声模型整体上一致性较好。当时间跨度较短时，估计出的最佳噪声模型较发散。时间跨度为5 a时，在E、N、U方向分别主要表现为FN+WN噪声模型、PL噪声模型，同时也包含其他噪声模型。随着时间跨度的增加，FN+WN噪声模型的比重逐渐上升，当时间跨度大于12.5 a时，E、N、U三坐标序列分量的噪声模型趋于稳定，且FN+WN模型占到50%以上，同时跨度大于15 a时，E向PL模型、GGM模型；N向及U向PL模型、FN+RW+WN模型所占百分比均在20%左右。另外需要注意的是，随着时间跨度的增加，随机游走噪声模型(FN+RW、FN+RW+WN)的比重有所增加，尤其是在N方向，在时间跨度为5～10 a时，仅2～3个测站呈现出最佳噪声模型为FN+RW+WN，当时间跨度增大到12.5～20 a时，约7个测站呈现出FN+RW+WN模型。这表明随着时间跨度的增加，GPS坐标序列中噪声的长周期分量(如随机游走噪声)变得显著，大跨度的时间序列为探测低频噪声的存在提供了条件，当时间序列不够长时，尤其是随机游走振幅较小时，被闪烁噪声等抑制，不能准确探测出来[11]。

2.2 不同时间跨度下噪声模型的演化过程分析

为了进一步分析不同跨度下噪声模型的演化过程，表4给出了24个IGS站N方向不同时间跨度下最佳噪声模型演化过程。

由表4可以看出：63%的IGS测站在跨度超过5 a后噪声模型发生了改变，即5 a的时间序列确定的噪声模型可靠性不高，存在较大的偶然因素；约50%的测站在10 a时间跨度中最佳噪声模型发生了改变，表明随着时间序列的增加，噪声模型趋于稳定。当时间跨度增加到12.5 a时，67%的测站最佳噪声模型不再改变，当时间跨度增大到15 a时71%的测站噪声模型不再改变。

同样，对坐标序列E方向最佳噪声模型随时间演化结果进行分析，结果表明，约62%的测站在5 a时间跨度后最佳噪声模型不再改变；当时间跨度增大到15 a跨度后约83%的测站最佳噪声模型不再发生改变。垂向坐标序列统计结果表明，58%的测站在5 a时间跨度后最佳噪声模型发生了改变，10 a时间跨度后趋于稳定，约71%的测站噪声模型不再变化。上述分析结果表明，当时间序列长度低于5 a时，噪声模型的不确定性较大，为了获得可靠的噪声模型估计结果，12.5 a跨度是比较理想的时间跨度间隔。

表4 不同跨度下噪声模型的演化过程(以N方向为例)

3 结 论

本文利用近20 a的24个IGS站GPS坐标时间序列数据分析了不同时间跨度对噪声模型的影响，得出了GPS噪声模型随着时间变化所发生的演化规律。结果表明：当时间序列跨度低于5 a时，噪声模型的不确定性较大，而12.5 a以上时间跨度的噪声模型趋于稳定且主要表现为闪烁噪声加白噪声，因此，为了获得更加可靠的噪声模型估计结果，12.5 a是比较理想的时间跨度间隔。同时，随着时间跨度的增加，GPS坐标序列中噪声的长周期分量(如随机游走噪声)变得显著，大跨度的时间序列为探测低频噪声的存在提供了条件，当时间序列不够长时，尤其是随机游走振幅较小时，被闪烁噪声等抑制，不能准确探测出来。

[1] 姜卫平,周晓慧.澳大利亚 GPS 坐标时间序列跨度对噪声模型建立的影响分析[J].中国科学(D辑:地球科学),2014,44(11):2461-2478.

[2] WILLIAMS S D P,BOCK Y,FANG P,et al.Error analysis of continuous GPS position time series[J].Journal of Geophysical Research:Solid Earth,2004,109(B3).

[3] LANGBEIN J.Estimating rate uncertainty with maximum likelihood:differences between power-law and flicker-random-walk models[J].Journal of Geodesy,2012,86(9):775-783.

[4] LANGBEIN J.Noise in GPS displacement measurements from Southern California and Southern Nevada[J].Journal of Geophysical Research:Solid Earth,2008,113(B5).

[5] MAO A,HARRISON C G A,DIXON T H.Noise in GPS coordinate time series[J].Journal of Geophysical Research:Solid Earth,1999,104(B2):2797-2816.

[6] 李昭,姜卫平,刘鸿飞,等.中国区域 IGS 基准站坐标时间序列噪声模型建立与分析[J].测绘学报,2012,41(4):496-503.

[7] 黄立人.GPS 基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学,2006,26(2):31-33.

[8] 袁林果,丁晓利,陈武,等.香港 GPS 基准站坐标序列特征分析[J].地球物理学报,2008,51(5):1372-1384.

[9] 田云锋.GPS 坐标时间序列中的异常高频周期性噪声[J].测绘科学,2011,36(1):26-28.

[10] MAO A,HARRISON C G A,DIXON T H.Noise in GPS coordinate time series[J].Journal of Geophysical Research:Solid Earth,1999,104(B2):2797-2816.

[11] SCHWARZ G.Estimating the dimension of a model[J].The annals of statistics,1978,6(2):461-464.

[12] AKAIKE H.Markovian representation of stochastic processes and its application to the analysis of autoregressive moving average processes[J].Annals of the Institute of Statistical Mathematics,1974,26(1):363-387.

[13] BOS M S,FERNANDES R M S,WILLIAMS S D P,et al.Fast error analysis of continuous GPS observations[J].Journal of Geodesy,2008,82(3):157-166.

[14] BOS M S,FERNANDES R M S,WILLIAMS S D P,et al.Fast error analysis of continuous GNSS observations with missing data[J].Journal of Geodesy,2013,87(4):351-360.

[责任编辑：刘文霞]

Performance analysis on GPS noise model with different time span

MA Mengran1, HE Xiaoxing1，2, HUA Xianghong1,3,4, SHU Ying1, GONG Guodong1

(1. School of Geodesy & Geomatics, Wuhan University, Wuhan 430079, China;2. School of Civil Engineer and Architecture, East China Jiao Tong University, Nanchang 330013, China; 3. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China; 4. Collaborative Innovation Center for Geospatial Technology,Wuhan 430079, China)

This paper describes the GPS coordinates of a time series model, and gives a GPS noise model, estimation methods and optimal noise model evaluation criteria. In this paper 24 IGS08core stations are proposed to quantitatively analyze the effect of different time span on GPS time series, and to explore the potential evolution as time changes. The results show that when the time span is shorter, the uncertainty of noise model is greater; the time span more than 12.5 years noise model mainly reflects flicker noise and white noise; the long-period component which has upward trend among the long time series in noise becomes significant.

GPS time series; time series span; noise model; impact analysis

引用著录：马梦然, 贺小星,花向红,等.时间跨度对GPS坐标时间序列噪声模型估计影响分析[J].测绘工程，2017，26(5)：25-28.

10.19349/j.cnki.issn1006-7949.2017.05.006

2016-05-06

国家自然科学基金资助项目(41174010，41374011，41464001，41374007);江西省数字国土重点实验室开放研究基金资助项目(DLLJ201605)

马梦然(1991-)，女，硕士研究生.

P228

A

1006-7949(2017)05-0025-04