利用小波变换进行GPS振动观测值的异常探测

王 涛,田林亚,侯建梅,殷 飞

(河海大学 地球科学与工程学院，江苏 南京 211100)

利用小波变换进行GPS振动观测值的异常探测

王 涛,田林亚,侯建梅,殷 飞

(河海大学 地球科学与工程学院，江苏 南京 211100)

本文利用小波变换技术进行GPS振动观测值的异常探测，将GPS振动观测值序列视为一组观测信号，先利用小波低频分解提取信号趋势，再利用小波高频分解探测异常值的位置，提出结合观测体自身变形趋势判断异常值是否存在，再通过小波高频分解和小波阈值去噪找到异常值准确位置的探测方法。结合某GPS振动平台上的振动观测实验数据进行仿真分析，获得准确的异常探测结果。实践证明文中研究的异常值探测方法是可行的和有效的，为GPS振动观测值的异常探测提供新思路。

小波变换；GPS；振动观测；异常探测；信号趋势；小波去噪

目前，高层建筑物日益增多，由于各种环境因素的作用，高层建筑物会产生振动和变形，对高层建筑物的结构振动监测是一项重要的工作。结构振动的频率和振幅是评价建筑物健康状况的主要指标[1-2]。GPS作为一种有效的实时动态测量手段，具有高精度、高采样频率以及可实现全天候实时自动化测量的优点，可采用GPS动态测量方法对高层建筑物进行实时的振动监测。受多种复杂因素的影响，GPS振动观测值中经常会出现一些异常值，异常值的存在会对后续的数据处理结果及其评判产生影响，甚至会导致错误的结论，因此，异常值的准确探测和分析对高层建筑物的结构振动监测十分重要[3]。

小波变换技术具有多尺度、多分辨率、可平移、可伸缩等优点，在时域和频域都具有表征信号局部特征的能力，在变形监测领域被成功地应用在观测信号的分析和处理[4-11]，其探测异常值的能力得到验证[12]，但对于具体如何准确探测和分析异常值的位置没有给出方法。小波变换技术能很好的提取GPS观测的振动信号，将GPS振动观测值序列视为一组观测信号，可以采用小波变换技术进行GPS振动观测值的异常探测。本文提出一种利用小波变换技术获得观测体的变形趋势图，将观测体的变形趋势与观测体的自身变化规律进行对比，先判断异常值是否存在，再通过小波分解和去噪来判断异常值位置的方法，并结合实例进行仿真分析。

1 小波变换基本原理

小波变换的基本思想是将信号分解成一系列小波函数的叠加，这些小波函数都是由一个小波基函数经过伸缩与平移形成的函数集合，小波变换可以视为被变换函数与小波函数作卷积的结果。设满足条件的小波基函数为φ(t)，小波基函数经过平移τ和伸缩a后得到

(1)

式中:τ为时移因子，a为尺度因子。将φa,τ(t)与信号f(t)作卷积，其连续小波变换式为

(2)

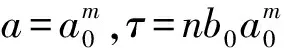
(3)

这时的小波函数就是离散小波，相应的离散小波变换为

(4)

小波变换是一个时间和频率的局部变换，能通过伸缩和平移等运算功能对信号进行多尺度细化分析，从而被称为“数学显微镜”。在此变换中，低频信号可以采用较低的时间分辨率来提高频率的分辨率，高频信号可以采用较低的频率分辨率来换取精确的时间分辨率。

2 异常探测基本思路

在GPS结构振动监测中，一般建筑物的振幅10～200 mm，其频率为0.1～10 Hz，其振动频率由结构体本身固有频率决定。由此可见在频率上表现为低频信号，并且振动在时间上是局部的[14]。异常值主要因各种观测噪声和观测环境的影响等产生，它们表现为分布在全局上的高频信号。异常值和正常值的时频特征一般是不一样的，在GPS振动观测值序列中，异常值的类型在理论上主要有孤立态、离散态、区域态三种[15]。

小波变换中，因为低频信号表现为信号的变化趋势，反映了事物有规律性的变化，据此，可以对观测信号进行小波低频分解提取观测体的变化情况，再与观测体的自身变化规律进行对比分析，或者与以往观测数据经处理后得到的趋势预测图进行对比分析，即可发现曲线异常值情况。高频部分表现为信号的各种噪声和异常值引起的不正常的突变，小波变换后高频部分模的极大值对应为原始信号中的异常点，可以根据原始观测值分解后的高频部分模的大小来判断异常值的位置，只要检测到了模极大值的位置，就等于找到了异常值。

3 仿真分析

本文采用香港理工大学GPS振动平台上的振动观测实验数据进行仿真分析。振动测试时，GPS接收机类型为 LEICA GXl230，GPS采样频率为20 Hz，卫星截止高度角为15°，振动平台的振动频率为0.025 Hz，在水平方向的振幅为5 mm，振幅模拟精度优于0.1 mm。

本文选取600个原始观测值序列作为一组观测信号，基于MATLAB软件平台对振动观测值进行小波变换与分析。原始观测值序列如图1所示，从图1中可以看出，原始观测值序列是一组平稳信号。

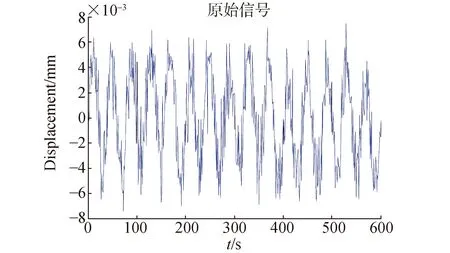
图1 原始观测值序列

在历元t=100时强制赋于10 mm孤立态异常值；在t=200、205、210时，分别设置12 mm、-14 mm、16 mm的离散态异常值；在t=440～460时，所有数据加上5 mm的区域态异常值，此异常值表现为某种系统误差引起；在t=540～560时，对所有数据强制赋给5 mm的区域态异常值，此异常值表现为信号失锁等原因引起的固定值误差。人为添加异常值后，含有异常值的观测值序列如图2所示。

图2 添加异常值后的观测值序列

由图2可以看出，两种区域态异常值可以被发现，但无法准确判断系统区域态异常值的位置，无法直接判断孤立态异常值和离散态异常值的准确位置，从图1和图2中也无法获得观测值序列的变化趋势。

3.1 信号趋势提取

在小波变换中，同一小波基函数在不同分解尺度下的信号趋势不同，当分解层数较少时，信噪比偏低，去噪效果不明显，信号趋势不明显，当分解层数过多时，会使信号信息丢失，产生失真，因此，合理选择小波分解层数来表示信号趋势极为重要。本文选择工程上采用的3 db小波[16]，研究不同分解尺度下表示信号趋势的差异。

首先对原始振动观测值序列进行小波低频分解，发现原始振动观测值序列中不含异常值，小波低频分解图(略)能够表示观测体的真实变化情况。对添加异常值后的振动观测信号进行1～8层小波低频分解，获得信号趋势如图3所示。观察信号分解图，可以发现信号在历元200附近、450附近和550附近出现异常波动，但整体呈现某种有规律的变化。从图中可以看出，1、2层信号平滑性和信噪比较低，光滑性差，但是时间分辨率高，信息量大。从第4～8层，信号逐渐表现为单一趋势，出现失真的情况，不能正确表示信号趋势。可以看出，3层分解能较好的反应振动信号的趋势，具有较好的时间分辨率、信号平滑度和信噪比，故认为3层分解表示信号趋势最优。

图3 添加异常值观测值小波低频分解

该振动为有规律的正弦波动形式，这与实验时设计的振动规律相同，可见，小波低频分解图可以准确表示观测对象的变化规律。在各层分解图中也可以看到信号由于异常值影响而出现的不正常抖动，异常值的存在使信号的低频分解表现为规律的失调，可见，异常值的存在严重影响了信号的趋势，这对于变形分析和安全预警是极为不利的，在工程应用时如发现这种情况，应根据实际情况分析该异常是因为观测粗差造成的还是观测体的真实变化引起的。

3.2 信号异常值判断

本次振动测试中，原始信号视为不含异常值的观测值序列，其变化趋势可以表示观测体的真实变化情况。将有异常值影响的趋势图(见图4(b))与原始信号趋势图(见图4(a))进行对比，发现信号异常情况。在一般工程实际中，高层建筑物受到风力、温度、日照以及地铁运行等因素的影响产生振动[17]，振幅一般随建筑物高度增加而增大，这些振动都具有一般规律性，在实际应用中可以针对具体的建筑物情况进行分析。

选择图像光滑、时间分辨率高、表现程度好的3层分解图进行对比分析，其对比图如图4所示。由图4中可以发现，在历元t=440～460和t=540～560处有区域态异常值存在，判断区域态异常值的位置。孤立态和离散态异常值在图4中也有体现，但是孤立态和离散态异常值的位置却不能准确判断。

图4 原始信号和有异常值信号的趋势图比较

3.3 含异常值的信号分解

信噪比、时间分辨率、信号真实程度采用db3小波，对含有异常值的观测值序列进行3层小波分解，结果见图5。由图5中可以发现，离散态异常值表现为高频部分，区域态异常值在低频部分表现较明显。在各层高频分解中，可以看到在历元t=205附近存在离散态异常值，有关文献认为据此判断异常值位置并进行优化，但是从图中很难准确判断异常值对应的历元，t=100时的孤立态异常值也不易发现。这是由于观测时噪声的干扰，使小波变换后异常值被平滑，对此可进行去噪处理。小波阈值去噪是一种实现简单、效果较好的小波去噪方法，采用该方法对3层分解后的第一层高频(cd1)部分信号进行默认阈值去噪，去噪结果如图6所示。

由图6可以明显看到孤立态异常值和离散态异常值的存在，并能根据对应历元判断异常值出现的位置，这样就准确探测出了异常值的位置。在数据处理中，如果确认该异常值属于粗差，就应该进行观测值的粗差剔除和修复，从而得到不含粗差的GPS振动观测值序列。

图5 含异常值的信号分解

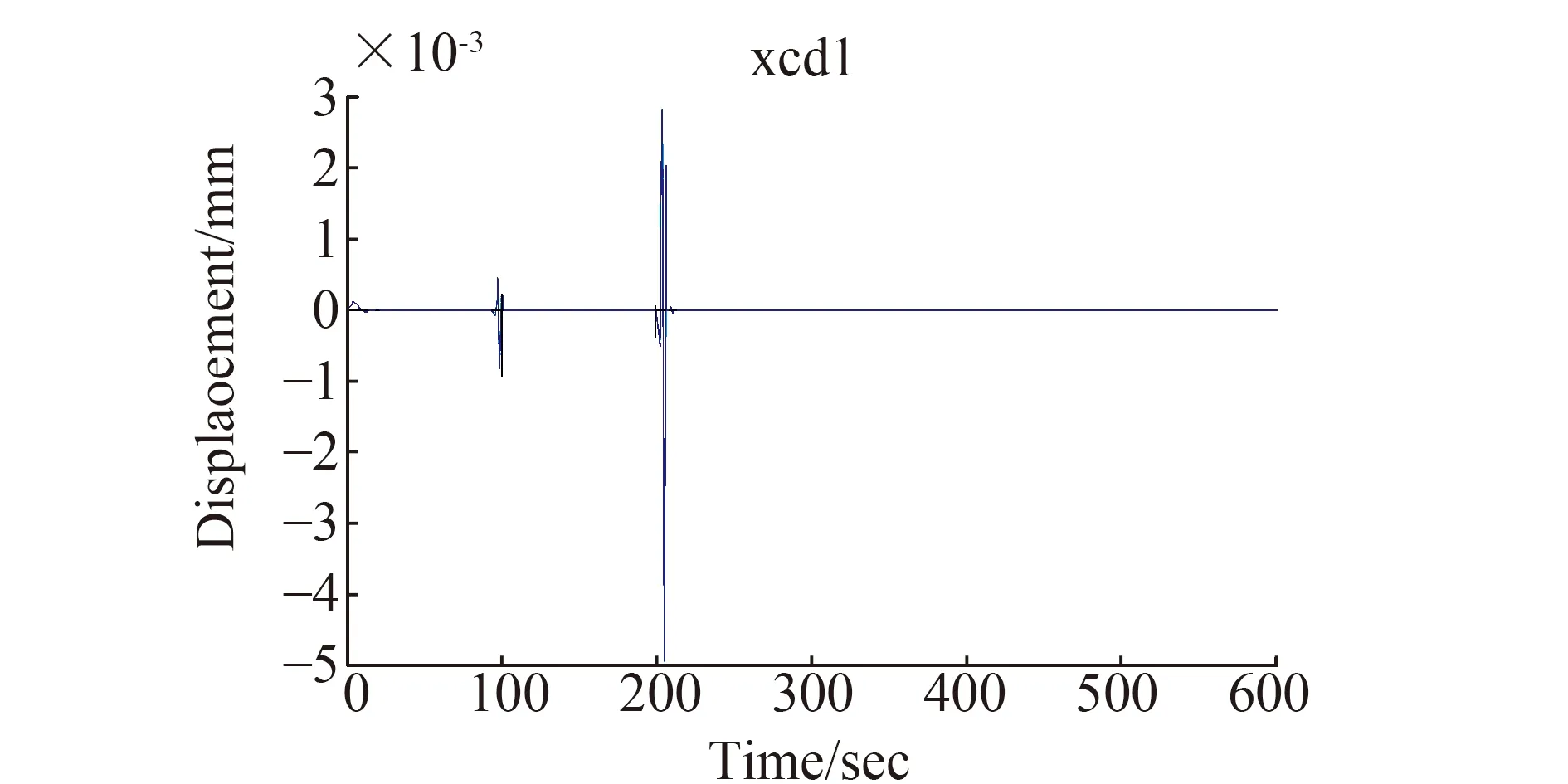
图6 高频信号小波去噪结果

4 结 论

GPS振动观测中可能存在由各种因素引起的异常值，直接对原始观测值序列进行小波变换时可能无法直接判断异常值是否存在，这时研究原始观测值序列的小波低频分解图可以获得观测体的变形趋势图，再与已掌握的观测体的自身变化规律进行对比，分析GPS振动观测值中是否存在异常值，再将异常历元的数据段进行高频分解获得详细异常值，但仍然可能因为各种噪声的影响还无法准确判断，这时对其进行小波去噪就可以进一步得到主要含异常值的信号图像，并能判断出异常值的准确位置。

本文研究GPS振动观测值的异常值探测方法，提出根据小波低频分解图获得信号趋势并与信号一般规律对比分析判断异常值的方法。采用小波低频分解能够提取原始观测值序列的变化趋势，其中小波3层分解在光滑性、时间分辨率和真实性等方面能更好地表达信号的特征，异常值的存在会严重影响信号的变化趋势，采用本文研究的方法可以准确有效地进行异常值的探测。

[1] 贺志勇,吕中荣,陈伟欢,等. 基于GPS的高耸结构动态特性监测[J].振动与冲击,2009,28(4):14-17.

[2] 匡翠林,戴吾蛟.GPS监测高层建筑风致振动变形及小波应用[J].武汉大学学报(信息科学版)，2010，35(9):1024-1028.

[3] 华锡生,田林亚.安全监测原理与方法[M].南京：河海大学出版社，2007：2-13.

[4] 夏秋,周金国.小波分析在GPS变形监测数据处理中的应用[J].地理空间信息,2011,9(6):40-41,44.

[5] 章浙涛.小波分析理论及其在变形监测中的应用研究[D].长沙：中南大学,2014.

[6] 夏开旺,田林亚,杨永平.基于小波分析的坝区GPS信号噪声研究[J].水电自动化与大坝监测，2006,30(4):51-55.

[7] 许杭，王俊杰，高俊强.小波分析去噪在腰沙围垦变形监测中的应用[J].测绘与空间地理信息，2016,39(3)：189-192.

[8] 冯小磊,华锡生,黄红女.观测值序列的粗差探测方法[J].水电自动化与大坝监测,2006,30(3)：56-59.

[9] 冷信风,赖祖龙,熊思桥.基于MATLAB与小波进行沉降数据处理与分析[J].测绘与空间地理信息,2014,37(2):180-182.

[10] 姚丽慧,高井祥,王坚.不同小波函数对异常值识别效果的比较[J].北京测绘，2011(3):20-23.

[11] 程龙，张晓梅.小波神经网络模型在高铁路基沉降预测中的应用研究[J].测绘与空间地理信息，2016,39(4)：218-221.

[12] 刘忠强,孙昌瑜.基于变形观测数据粗差探测与修复的小波变换法[J].测绘与空间地理信息,2013,36(12)：224-226.

[13] 王慧琴.小波分析与应用[M].北京：北京邮电大学出版社,2011:60-68.

[14] 钟萍,丁晓利,郑大伟,等.GPS结构振动监测数据滤波方法及其性能实验研究[J].测绘学报,2007,36(1):31-36,42.

[15] 王坚,高井祥,苗李莉.强污染单历元GPS形变信号的提取和异常值识别[J].武汉大学学报(信息科学版)，2004,29(5)：416-419.

[16] 党星海,赵丽洁,孔令杰,等.小波分析在GPS振动监测数据中的应用[J]. 大地测量与地球动力学,2013,33(2):147-150.

[17] 曹艳梅,夏禾,战家旺.运行列车引起高层建筑物振动的试验研究及数值分析[J]．工程力学,2006,23(11):182-187,152.

[责任编辑：李铭娜]

本刊郑重声明

近来，在一些搜索引擎上，经常充斥一些假冒网站、机构及个人以《测绘工程》杂志社名义征稿、组稿、代发论文，收取审稿费、代写费、版面费，欺诈投稿人，严重损害了我刊名誉。据查其刊名及国内统一刊号、国际标准刊号纯属盗用；发给作者的用稿通知上所盖公章纯属伪造。所谓的征稿行为已涉嫌侵权、诈骗、伪造企事业单位公章等多项犯罪，本刊已向公安机关报案。

本刊敦促相关网站及个人立即停止这一严重损害我刊名誉的侵权行为，本刊将依法保留追究有关人员法律责任的权利。特此声明!

获取在线投稿平台地址邮箱:chgc2008@vip.com,咨询电话:0451-88028906

(本刊编辑部)

Using wavelet transform to detect GPS vibratory observation data

WANG Tao,TIAN Linya, HOU Jianmei， YIN Fei

(School of Earth Science and Engineering, Hohai University, Nanjing 211100,China)

This paper presents the wavelet transform technology to detect GPS vibratory observation data, regarding GPS vibratory observation data order as a group of observation signal. Firstly it studies how to extract the signal trend by wavelet decomposition of low frequency, and then use high frequency wavelet decomposition to detect the location of abnormal data. A method of detection abnormal data combined with the construction deformation trend is proposed to judge whether the abnormal data exist, and then to find abnormal data accurately position through high frequency wavelet decomposition and wavelet threshold denoising. Combining the vibratory observation experimental data in some GPS vibration platform, it mates a simulation analysis to obtain an accurate anomaly detection result. This method proves to be effective and feasible, which can provide a reference for the anomaly detection..

wavelet transform; GPS; vibratory observation; anomaly detection; signal trend; wavelet denoising

引用著录：王涛,田林亚,侯建梅，等.利用小波变换进行GPS振动观测值的异常探测[J].测绘工程，2017，26(5)：52-56.

10.19349/j.cnki.issn1006-7949.2017.05.011

2016-05-12

王 涛(1992-)，男，硕士研究生.

P228

A

1006-7949(2017)05-0052-05