飞行器航路点飞行仿真模型研究*

程 铭 严宗睿 宋 勇

(海军指挥学院 南京 210016)



飞行器航路点飞行仿真模型研究*

程 铭 严宗睿 宋 勇

(海军指挥学院 南京 210016)

针对常用的简化的航路点飞行模型,提出了考虑地形跟随和常高度率的飞行算法,并在空气动力学飞行以及非空气动力学飞行模型中如何加入地形跟随算法和常高度率算法,最后给出计算的实例演示。

飞行器; 航路点飞行; 地形跟随

Class Number TP391.9

1 引言

航路点飞行是飞行器编队的常用的作战行动,即飞行器编队按顺序以规定的速度从一个航路点飞行到另一个。在常用的仿真模型计算中,通常把航路点飞行进行了简化考虑,一个航路点只包含有经纬度、高度、速度、到达时间、离开时间。而这些简化的航路点信息并不满足仿真粒度更小的需求,需要更进一步考虑的考虑地形跟随信息、航路点行为方式、军事坐标参考系统等。而且在飞行过程中也有可能会被执行战场管理功能的指控模型打断,如加油、防御等,在执行完其他任务后,往往需要继续执行未完成的航路点飞行任务。

飞行器编队的航路点飞行行为一般有两个来源,一是由用户通过想定方案的规划产生,二是在执行任务的过程中,由飞行器根据指控模型的决策转换为其他的行为模式。当指控命令飞行器继续正常运行时,则该飞行器返回航路点模式。当编队的长机到达最后的航路点时,飞行处理模型将僚机改变为航路点模式,这样僚机也能飞到最后的航路点。

2 地形跟随算法

2.1 地形跟随飞行

在飞机的所有飞行模式中,会在需要时调整方向向量以避免飞机超过了高度限制或与地形冲突。调整是通过采用一个高度率的过阻尼反馈控制循环来实现的。本文所提及的算法所采用的地图坐标都是ECEF坐标,所以飞机的位置使用一个三维向量来表示。

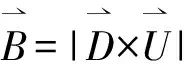
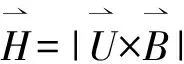
接下来,找到计划飞行路径水平方向的地形高度。未来,飞机的位置沿这个水平方向随时间发生变化:

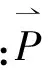
利用这个方程,根据事先仿真设置的地形跟随参数就可找到未来的a/c位置。首先找到初始Dt时间后飞机的位置,后续的位置会从初始Dt值向前几何增长,用连续时间间隔乘以乘数因子。对每一个这样计算的位置,会通过地图数据库找到相应的地形高度。对特殊情况,期望高度是通过MSL测量的,地形高度设为0.0。地形采样会重复进行,直到收集到指定数量的地形采样。控制参数的默认设置允许进行8次地形采样,从0.5s开始,以1.5的因子递增。默认设置的地形采样是在飞机的当前位置之前,时间范围是从0.5s～8.5s。一旦找到未来位置的地形高度,当飞机下降或进行地形跟随时,就将使用的期望下限高度(floor altitude)设为用最高的地形高度。

一旦找到期望的飞机高度,飞机实际的高度率就可通过找到飞机速度向量在本地垂直方向的分量来确定:

接下来,会找到当前位置H和期望高度HDes之间的高度差ΔH:

ΔH=HDes-H

然后计算期望的高度率,调整过阻尼的反馈控制循环:

其中,VV是期望的高度率(m/s),ΔH是当前位置和期望高度之间的高度差(m),Gain是过阻尼反馈循环的增益,DtStep是积分步长=0.5(s)。

前面方程中的增益是仿真模型可输入的地形跟随控制参数,在这里设置为15。

如果实际的高度率大于期望的,或如果在地形跟随中,需要重新计算方向向量以避免超过高度限制或飞向地面。首先,计算水平面中的a/c速度,假设垂直平面内的速度是期望的高度率:

其中,VH是水平方向的飞机速度(m/s),Vmag是a/c速度向量的大小(m/s),VV是飞机期望的高度率(m/s)。

如果期望的高度率大于当前的a/c速度,则VH设为0,期望的高度率设为Vmag。在地形跟随时,对爬升角度有限制以阻止飞机快速改变高度。最大爬升角度限制是一个在飞机元素窗口输入的控制参数,它的默认设置是20°,由速度方向形成的爬升角度确定如下:

其中,φ是爬升角(°),VV是飞机期望的高度率(m/s),VH是在水平方向的飞机速度(m/s)。

如果爬升角大于最大爬升角,用最大爬升角重新计算水平速度:

其中,VH是在水平方向的飞机速度(m/s),Vmag是a/c速度向量的大小(m/s),θMax是最大爬升角落(°)。

然后计算相应的高度率:

VV=VH×tan(θMax)

其中,VV是飞机期望的高度率(m/s),VH是在水平方向的飞机速度(m/s),θMax是最大爬升角(°)。

一旦计算出了水平和垂直速度,就可把速度应用到适当的方向上计算新的方向向量:

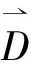
1) 高度监测

当一个飞机不进行地形跟随时,如果要求飞机保持飞行在下限高度之下或升限高度之上,就要调整方向向量。除了航路点和僚机模式,所有的飞行模式采用默认的下限高度和升限高度分别是200m和100000m。对航路点和僚机模式,升限高度仍然是100000m,但下限高度取决于指定的高度。对航路点模式,下限高度设为最小指定高度和200m。对僚机模式也一样,如果编队长机正在飞航路点模式的话,下限高度根据相同的最小条件设置。所有模式的下限高度都是在地平之上(AGL),所有模式的升限高度都是MSL。

为了执行如地形跟随算法所述的高度监测和方向向量调整,需要设置期望的高度。如果飞机没有进行地形跟随,且它的实际高度率是负数(飞机正在下降),或如果它的实际高度小于下限高度,则期望高度设为下限高度。对除了地形跟随以外的其它情况,期望高度高设为升限高度。

2) 地形跟随

当一个飞机预设好飞地形跟随模式时,会对方向向量进行调整以保持飞机飞行在指定高度。在地形跟随时,只有下限高度是重要的。对这种情况,在配置平台时将它设为由用户输入的指定高度。为了执行地形跟随要采用地形跟随算法所述的方向向量调整,期望高度自动设为下限高度。

2.2 常高度率飞行

当一个飞机正在飞航路点、交战或RTB飞行模式时,要对每种模式情况下计算出的方向向量进行修正以满足地球曲率。当期望位置和当前位置向量之间有差异时,每种模式都要计算方向向量,这可能会产生一个穿过地球直接指向期望位置的方向向量。这个方向向量指向期望位置,但是要沿着地球表面。此外,当改变高度时,飞机实际上并不是飞直线,而是沿地球曲率飞一个类似抛物线的航迹。在常高度率飞行中,对这些现象都有考虑。

为了重新计算方向向量,先用地图数据计算出当前位置高度和目标位置高度,再用目标高度减去当前高度,计算出它们之间的差异ΔH。

接下来,再用余弦定理计算出飞机当前位置向量和期望位置向量之间的夹角:

其中,φ是当前位置向量和目标向量之间的夹角(rads),DPmag是目标位置向量的幅度(m),PMag是当前位置向量的幅度(m),DMag是起始方向向量的幅度(m)。

以当前指定速度到达目标点的时间由下式计算:

其中,TTG是到达目标点的时间(s),PMag是当前位置向量的幅度(m),φ是当前位置向量和目标向量之间的夹角(rads),ΔH是当前位置和期望高度之间的高度差(m),VCmd是指定速度(m/s)。

现在,用这个时间可以计算出高度率VV:

给出指定速度和高度率结果后,沿地球表面的速度VH可由下式计算:

接下来,在飞机当前位置上垂直于地球表面的向量,可由方向向量和飞机当前位置的本地上向量叉乘得到:

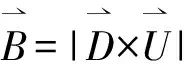
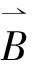
结果向量垂直于飞机当前位置的地平面,那么,这就是在水平方向的向量。接下来,计算水平方向向量的单位向量:

知道了水平和垂直方向的单位向量后,下面可以应用每个方向的速度:

VECIN=VH×UEHN+VV×U

其中,VECIN是飞机在ECEF中的速度向量(m/s),VH是沿地球表面的速度(m/s),UEHn是水平单位向量在第n个方向的分量(m),VV是高度率(m/s),U是垂直单位向量在第n个方向的分量。

最后,通过将积分步长dt用到最终的速度向量上以得到新的方向向量DN:

DN=VECIN×dt其中,VECIN是速度向量在第n个方向的分量(m/s)。

如果新的方向向量不能让飞机飞到升限高度以上或下限高度以下,则用它在积分时间步长上积分飞机的位置。如果这个向量导致飞机超过了高度限制,就要对方向向量进行调整以监测高度,如地形跟随算法所述。

3 航路点飞行计算

关于飞行器编队的空中飞行运动的计算有两种方式:第一种方式是利用典型的空气动力学,在仿真更新的步长内对飞机的位置和速度进行积分。在计算达到期望的速度所需的加速度时,要考虑推力、重力、升力和阻力,并加入地形跟随的考虑。第二种模式是利用非空气动力学对飞机的位置和速度进行积分,同时也要考虑地形跟随的因素。两种模式的计算方法分析如下。

3.1 空气动力学航路点飞行

如果编队长机的飞行仿真并没有特别指明要采用非空气动力学航路点的飞行模型,或者长机刚从作战行动中返回,还没有到达航路中的下一个航路点,则使用典型的空气动力学飞行模型。

当一个飞机飞向它的目标航路点时,飞机的积分时间DT初始化为飞机的上一次仿真更新时间。那么,指定速度初始化为飞机最大速度的最小值和用户为目标航路点定义的速度。如果飞机是一个被指控模型命令悬停的直升机,则将指定速度设为0以迫使直升机减速为悬停状态,并且指定速度将一直设为0直到指控模型发送一个交战行动指令以前进到下一个航路点。

指定的转弯重力是根据飞机当前飞行的路径类型来初始化的,如果在一个圆轨道上飞行,重力设为3.0。否则,就设为该飞机结构允许的最大重力。最后,如果目标航路点要使用地形跟随,飞机将用地形跟随方法飞到该航路点。

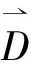
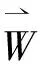
从平台到目标向量之间的距离计算如下:

其中,Dmag是方向向量的幅度(m),Dn是方向向量在第n个方向的分量(m)。

接下来,计算飞机的转弯半径,如果飞机飞得比它的角速度快,它的转弯半径由下式计算:

其中,RT是转弯半径(m),V是飞机当前的速度(m/s),Gcmd是指定转弯重力。

如果飞机飞得比它的角速度慢,则转弯半径RT由下式计算:

到达航路点必须满足两个标准,一是飞机的转弯半径必须大于与航路点之间的剩余距离,二是飞机的速度向量必须垂直于或大于从航路点到飞机飞行路径的投影线。如果这些标准满足,该航路点就是最后一个,飞机执行下一个任务。如果没到最后一个航路点,就将飞机更新到下一个航路点,且它的飞行目标高度调整为下一个航路点的高度。飞机也可使用新目标点的地形跟随状态,并重新设置指定速度,使用上述计算方法的重新计算到新目标航路点的方向向量。

如果引入地形的因素,则需要调整方向向量以满足地形跟随或地球曲率。如果目标航路点需要地形跟随,就采用2.1所述地形跟随方法修正方向向量,由定义可知这个方法已经考虑了地球曲率,地形跟随采用的下限高度由指定的AGL高度来设置。

如果地形跟随不必要,只考虑地球曲率的方向向量修正,则通过使飞机维持一个常数高度率飞行实现的,2.2节中解释了常数高度率的方法。如果方向向量导致飞机飞得高于升限高度或低于下限高度,就如2.1节的方法进行监视高度来调整。高度监测中升限高度默认为100000m,下限高度设为最小的200m或指定的AGL高度。

然后,飞机在积分时间间隔内沿方向向量飞行,对每次积分,积分时间由下式更新:

DT=DT+dt其中,DT是飞机总的积分时间(s),dt是积分步长(s)。

在积分时,飞机在航路点之间按直线或按曲线飞行,这个过程会重复执行直到DT超过了当前的仿真时间。

3.2 非空气动力学航路点飞行

如果一个飞行器编队的长机选择了非空气动力学的飞行计算,且长机正在飞航路点模式,则不考虑飞机的空气动力学和结构限制,对飞机位置和速度进行积分。和空气动力学航路点飞行模型一样,非空气动力学航路点的飞行计算也在每个积分步长上进行积分,直到该仿真步长结束。当到达仿真步长的更新间隔时间时,将飞机新的位置和速度传送给其他仿真模型。

航路点之间的速度是通过在前一个和下一个航路点速度之间用线性内插的手段调整的,首先,找到目标航路点相对于前一个航路点的位置:

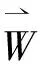
接下来,可以计算出当前和前一个航路点之间速度差的幅度ΔV:

ΔV=VCurr-VPrev

其中,ΔV是当前和前一个航路点之间的速度差(m/sec),VCurr是目标航路点速度的幅度(m/s),VPrev是前一个航路点速度的幅度(m/s)。

这样,指定速度就可通过在航路点期望速度之间线性内插来设置:

其中,VCmd是指定速度(m/s),VCurr是目标航路点速度的幅度(m/s),ΔV是当前和前一个航路点之间的速度差(m/s),Dmag是方向向量的幅度(m),WMag是当前和前一个航路相对位置向量的幅度(m)。

如果该飞机是由指控模型命令进行悬停的直升机,这个指定速度设为0.0以强制直升机减速到悬停。这个指定速度将持续设为0.0直到指控模型发送一个交战行动指令,命令该直升机飞行到下一个航路点。

利用这个指定速度,就可根据下式计算期望的加速度:

其中,AMag是需要加速度的幅度(m/s2),VCmd是指定速度(m/s),V是飞机当前速度的幅度(m/s),Dt是积分时间步长(s)。

一旦如2.1节和2.2节所述根据高度限制和地球曲率对方向向量进行了调整,就将当前速度和需要的加速方向向量进行应用以得到新的速度和加速度向量:

然后用速度和加速度向量更新飞机的状态:

重复以上这个过程直到到达仿真步长的更新时间。使用该非动力学飞行的计算方法,飞机的转弯是瞬间完成的。

4 航路点飞行处理流程

根据以上所述的讨论,在加入了地形跟随算法矫正的航路点飞行处理流程如下。

图1 航路点飞行处理流程

1) 获取平台当前的位置和速度,并计算到下一个航路点的方向向量和距离,设置过载数值;

2) 判断是否到本次更新的最终时间,如果是,则更新平台的位置和速度,并继续转到1)。如果否,则进行以下的步骤;

3) 计算到下一个航路点的方向和距离,确定转弯半径;

4) 使用地形跟随处理矫正飞行方向;

5) 如果距离降落基地小于1000m,则各方向上都使用指令速度;

6) 根据飞行方向确定直线飞行还是曲线飞行,并向前飞行一个积分时间步;

7) 更新速度方向矢量,计算转弯半径;

8) 如果转弯半径大于平台到基地的距离,则平台着陆;

9) 时间加上一个积分步长,并转入2)。

5 实例演示

根据上述航路点飞行的算法,实现的某飞机的飞行路径如图2所示,这是没有加入地形跟随的飞行方式。

图2 普通航路点飞行

加入地形跟随算法后,输出到三维态势显示的飞行路径如图3所示。

图3 加入地形跟随的航路点飞行

6 结语

由以上实现的两个仿真实例可以看出，没有加入地形跟随算法的飞行器航路点的飞行路径是二维平面的，无法适应考虑地形影响的仿真环境，甚至会出现穿山而过的情况。而加入了地形跟随算法的航路点飞行仿真模型不仅能适用有地形影响的航路点飞行，还能考虑到地形对于雷达探测等的遮蔽效果，从而使飞行器能适时调整飞行路径，达到规避雷达探测的目的。

[1] PKA Menon, VHL Cheng, E Kim. Optimal trajectory synthesis for terrain-following flight[J]. Journal of Guidance Control & Dynamics,2012,14(4):807-813.

[2] 彭卫,柳健,王长青,等.一种基于地形跟踪的航迹优化算法[J].华中科技大学学报:自然科学版,2004,32(8):79-81. PENG Wei, LIU Jian, WANG Changqing. Route Optimization Algorithm Based on Terrain Tracking[J]. Journal of Huazhong Univ. of Sci. & Tech,2004,32(8):79-81.

[3] 赵小勇,杨恒辉.一种新的地形跟随飞行方法与关键技术研究[J].计算机测量与控制,2012,7:1983-1985. ZHAO Xiaoyong, YANG Henghui. Study on Key Techniques of a New Approcach to Terrain-following Fight[J]. Computer Measurement & Control,2012,7:1983-1985.

[4] 周坦胜,熊霄,安锦文.地形跟随飞行控制系统的仿真研究[J].系统仿真学报,2009,24:7798-7800. ZHOU Tansheng, XIONG Xiao, AN Jinwen. Simulating Research of Flight Control System of Terrain Following[J]. Journal of System Simulation,2009,24:7798-7800.

[5] 卢斌文,曲东才,杨晓龙.基于数字地图的地形跟随系统设计与仿真[J].四川兵工学报,2016,6:103-105. LU Binwen, QU Dongcai, YANG Xiaolong. Design and Simulation of Terrain Following System Based on Digital Map[J]. Journal of Sichuan Ordnance,2016,6:103-105.

[6] 李建军,李钊,陈超.低空突防中地形跟随算法研究[J].计算机与网络,2009,17:56-58. LI Jianjun, LI Zhao, CHEN Chao. Research of Terrain Following Algorithm for Low Altitude Penetration[J]. Computer & Network,2009,17:56-58.

[7] 唐一萌.基于模糊控制方法的自动地形跟随系统设计[J].计算机仿真,2010,2:59-63. TANG Yimeng. Design of the Automatic Terrain Following System of Aircraft Based on Fuzzy Controller[J]. Computer Simulation,2010,2:59-63.

[8] 王雯.基于模糊抑制函数的地形跟随控制技术[J].计算机仿真,2013,7:106-109. WANG Wen. Fuzzy Stay Function Based Terrain Following Control Technology[J]. Computer Simulation,2013,7:106-109.

[9] 陈楸,杨文萍,朱红铃.地形跟随飞行轨迹设计与仿真验证[J].计算机仿真,2012,03:113-116. CHEN Qiu, YANG Wenping, ZHU Hongling. Design and Simulation of Terrain Following Flight Path[J]. Computer Simulation,2012,3:113-116.

[10] 覃东升,方勇.一种巡航导弹地形跟随算法的研究与实现[J].计算机仿真,2012,2:50-53. QIN Dongsheng, FANG Yong. Study and Implement of Cruise Missile Terrain Following Algorithm[J]. Computer Simulation,2012,2:50-53.

Waypoints Flight Simulation Model of Aircraft

CHENG Ming YAN Zongrui SONG Yong

(Navy Command College, Nanjing 210016)

In view of the commonly used simplified waypoint flight model, the flight algorithm considering terrain following flight algorithm and constant altitude is proposed. and how to use the two algorithms in the air flight dynamics and non air flight dynamics model. Finally, the calculation example is given.

aircraft, waypoint flight, terrain following

2016年7月10日,

2016年8月30日

程铭,女,副教授,研究方向:作战模拟、系统仿真。严宗睿,男,博士研究生,研究方向:系统仿真。宋勇,男,硕士研究生,研究方向:军事运筹。

TP391.9

10.3969/j.issn.1672-9722.2017.01.013