连续、离散小波变换的桥梁健康检测方法研究

陈雪冰尤文贵

(福建农业职业技术学院福建福州350007)

连续、离散小波变换的桥梁健康检测方法研究

陈雪冰尤文贵

(福建农业职业技术学院福建福州350007)

选取竖向位移模态和曲率模态，分别采用连续小波变换和离散小波变换对其进行损伤检测。数值模拟结果表明:当采用连续小波变换时，基于竖向位移的小波变换并不能准确确定损伤位置，而基于曲率的小波变换可以准确确定结构损伤位置;当采用离散小波变换时，基于曲率和竖向位移的小波变换都可以准确确定结构损伤位置。

连续小波变换;离散小波变换;曲率;小波基选择

1 概述

由于荷载作用和外部环境的侵蚀，桥梁结构出现一些轻微损伤，随着服役时间的增长，这些轻微损伤会逐渐演变成大损伤进而影响结构的使用安全，尽早发现并修复这些轻微损伤将可以延长结构使用寿命，保证结构使用安全。小波变换可以检测出信号细微变化，使用小波变换可以检测出桥梁结构轻微损伤。

在桥梁损伤检测中可以采用连续小波变换、离散小波变换、小波包变换，离散小波变换是将小波基函数的尺度因子和平移因子离散化，小波包变换是将信号的低频部分进一步分解。余竹［1－3］等分别采用上述3种方法对桥梁损伤进行检测研究，但是并未对这3种方法优劣进行比较。本文通过数值模拟对连续小波变换和离散小波变换在桥梁检测中的优劣进行比较。

2 基于小波变换的损伤识别

2.1 小波变换

函数的连续小波变换表达式为:

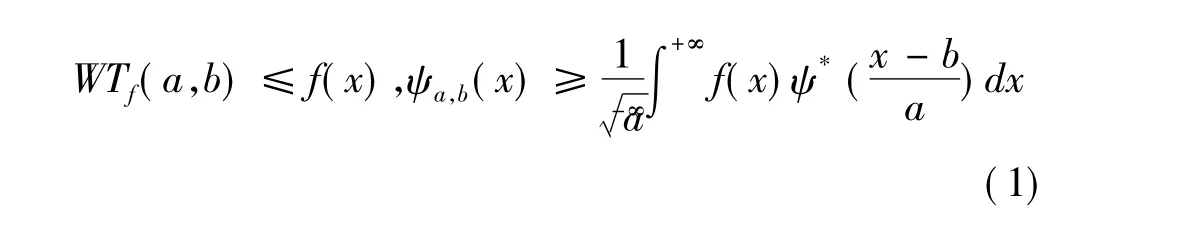
其中:ψ(x)为小波母函数，ψ*(x)为ψ(x)的共轭，a，b分别为尺度因子和平移因子。其中ψ(x)的傅里叶变换φ(ω)必须满足容许条件:

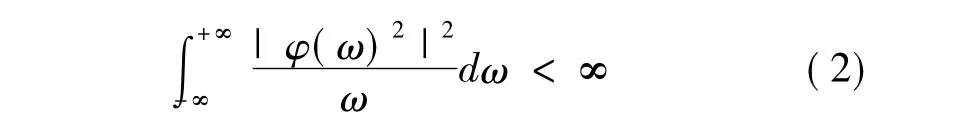
将a，b离散化，令a=2m，b=n·2m，n∈Z则有的离散小波变换为

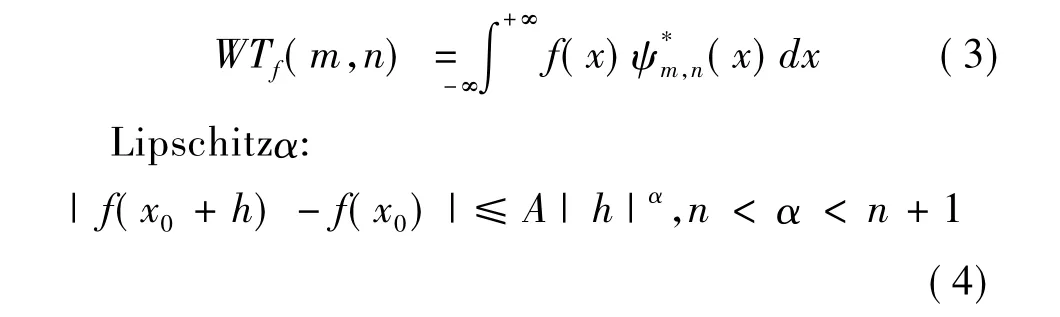
α称为f(x)在x0处的Lipschitz指数，Lipschitz α表征了函数f(x)在x0处奇异性的大小，α越大，函数在x0处的光滑度越高;α越小，函数在x0处的光滑度越低。若f(x)在x0处可导，则α≥1;若f(x)在x0处不连续但有界，则0≤α≤1。已经证明Lipschitz α与小波变换模极大值之间存在如下关系:

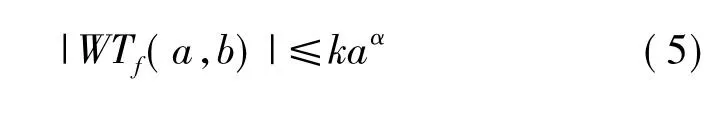
当α＞0时，小波变换的极大值随尺度α的增大而增大;当α＜0时，小波变换的极大值随尺度α的减小而减小。

理论表明，若信号f(x)在x0处是突变点，那么在各个尺度上x0点附近的小波变换都会产生一个局部极大值点。

小波基的消失矩定义:

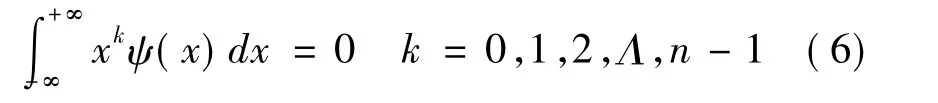
若ψ(x)有n个连续的零点，则称ψ(x)的消失矩为n。几种小波基的消失矩阶数，如表1所示:

表1 小波基消失矩阶数

推论［4］:设小波ψ(x)具有紧支撑和n阶消失矩，且n次连续可微。若f(x)在x0处Lipschitz指数为α，且n＞α，则WTf(a，b)在x0处取极大值。

从推论可以看出小波基的消失矩必须大于结构损伤处模态的Lipschitz α，只有满足这个条件才可以很好地检测出结构的损伤位置。

小波基还应满足如下条件［5］:

①紧支性;②正则性;③对称性;④消失矩阶数。

2.2 结构损伤位置判别

根据欧拉梁理论，结构在截面损伤位置处存在如下关系:

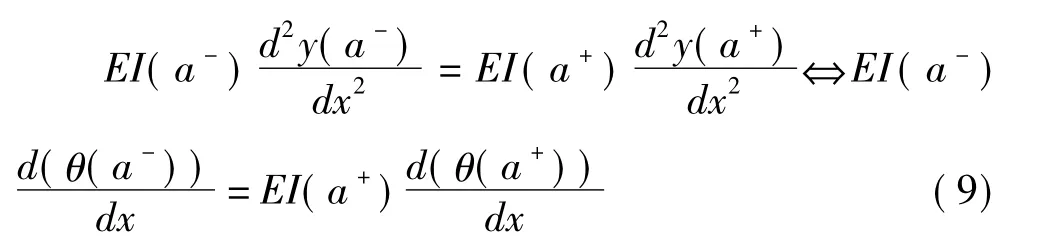
2.3 曲率的求解

在进行结构检测时，通常只能检测到节点的位移、速度、加速度等参数，节点的曲率较难获得，根据微分思想，可以通过节点的位移求得节点的近似曲率，如图1所示，曲率的计算步骤如下。

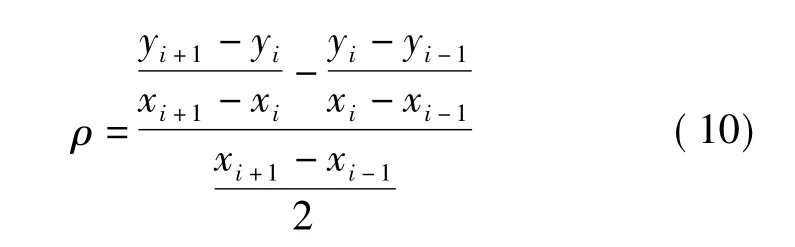
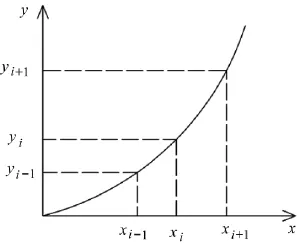
图1 曲线点(xi，yi)处曲率示意图

3 数值模拟

本文采用ANSYS对矩形一悬臂梁进行数值模拟，梁长3m，梁断面尺寸b×h=0．03m×0．05m，弹性模量E=3．0×104MPa。因为结构损伤均可以表示为弹性模量的降低，所以本文采用弹性模量降低来模拟结构损伤，结构损伤处的弹性模量降低15％。采用ANSYS将梁等分成500个单元，有损伤梁的单元号为230。选取Db3小波基进行小波变换。分别采用竖向位移，曲率作为小波变换的输入。

3.1 基于竖向位移模态的损伤检测

选用竖向位移模态，分别采用连续小波变换和离散小波变换得到的结果，如图2所示。

由图2可以看出，当采用竖向位移模态作为小波变换输入时，连续小波变换的灰度图不能准确识别结构的损伤位置，而离散小波变换可以准确识别出结构在第230个单元附近存在损伤。

3.2 基于曲率模态的损伤检测

选用曲率模态，分别采用连续小波变换和离散小波变换得到的结果，如图3所示。

由图3可以看出，节点——曲率图可以指出结构的损伤位置在第230个单元附近，当采用Db3连续小波变换和离散小波变换都可以确定结构损伤位置，但采用离散小波变换能显著地确定结构损伤位置。

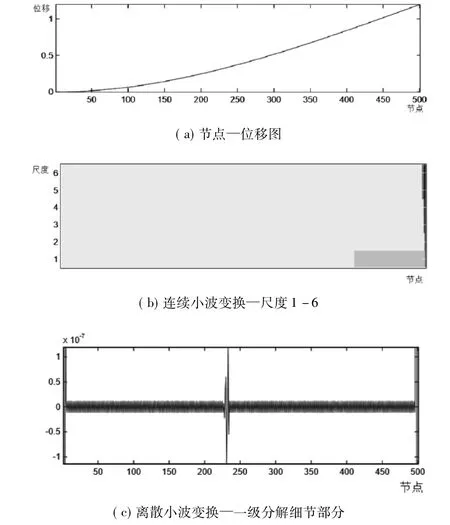
图2 竖向位移模态损伤检测图

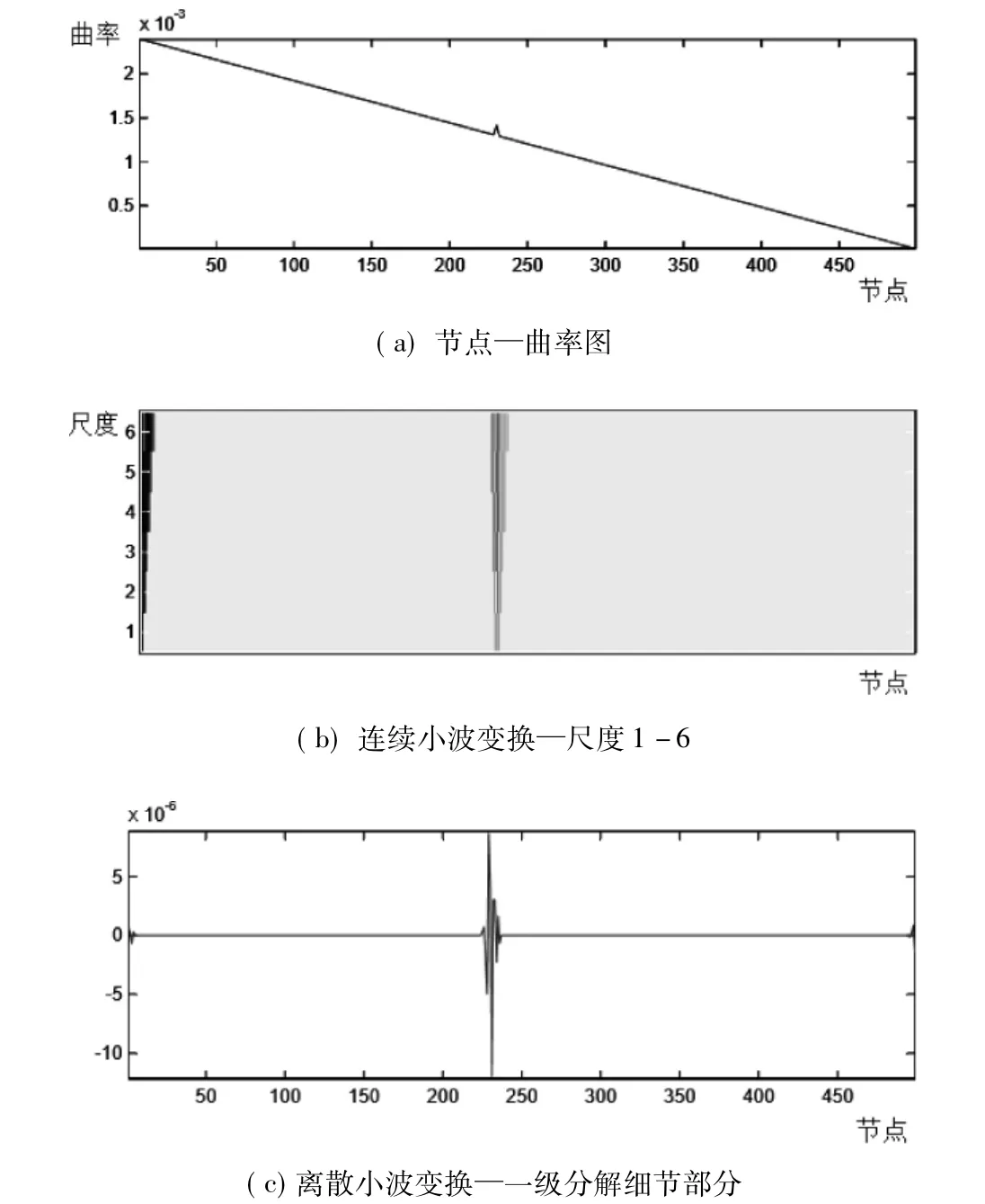
图3 曲率模态损伤检测图

4 结论

本文以悬臂梁为例，分别选取竖向位移模态和曲率模态进行小波变换，得到如下结论:

(1)数值模拟结果表明基于位移模态的结构损伤检测，离散小波变换比连续小波变换更有优势;

(2)当选取曲率模态时，连续小波变换和离散小波变换都可以检测出结构的损伤位置。

综上所述:用小波变换进行结构损伤检测时，采用曲率模态比位移模态有优势，采用离散小波变换比连续小波变换有优势。

［1］余竹，夏禾．基于移动荷载作用下的结构响应及小波分析的桥梁损伤诊断［J］．北京交通大学学报，2014，38 (3):55．

［2］郭健，孙炳楠．基于小波变换的桥梁健康监测多尺度分析［J］．浙江大学学报:工学版，2005，39(1):114－118．

［3］丁幼亮，李爱群，姚晓征．动载测试与小波分析在桥梁结构损伤诊断中的联合应用［J］．振动工程学报，2006，19 (4):499－504．

［4］张兆宁，廖一原，刘峡，等．缓变信号奇异性的小波变换检测及其应用［J］．系统工程理论与实践，2000，10(10): 84－88．

［5］魏宝琴，李白萍．最优小波基的选取原则［J］．甘肃科技，2007，23(10):42－43．

The research method on bridge health detection based on continuous and discrete wavelet transform

CHEN XuebingYOU Wengui
(Fujian vocational college of agriculture，Fuzhou 350007)

The vertical displacement and curvature are selected in this paper，using continuous wavelet transform and discrete wavelet transform to detect the damage respectively.The numerical simulation results indicates that when continuous wavelet transform is being used，the wavelet transform based on curvature can exactly determine the location of the damage and on vertical displacement can’t;when discrete wavelet transform is being used，the wavelet transform based on vertical displacement and curvature can both determine the location of the damage.

Continuous wavelet transform;Discrete wavelet transform;Curvature;The selection of wavelet basis

U446

:A

:1004－6135(2017)01－0069－03

陈雪冰(1983．2－)，男，助教。

E-mail:chngxuebing@126．com

2016－10－11