迷宫式汽封流体动力特性研究
2017-02-08马浩原张万福
马浩原,张万福, 2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海理工大学 能源与动力工程学院,上海市动力工程多相流动与传热重点实验室,上海 200093)
迷宫式汽封流体动力特性研究
马浩原1,张万福1, 2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海理工大学 能源与动力工程学院,上海市动力工程多相流动与传热重点实验室,上海 200093)
建立了迷宫式汽封的全三维模型,采用CFD商业软件Fluent对不同工况下汽封的流场进行了计算分析,研究了转子所受的气流力与转速、进出口压力比及偏心率的关系,得到了影响转子稳定性的密封动力特性系数和涡动系数.结果表明:随着转速、进出口压力比和偏心率的增大,涡动系数也相应增大,转子的稳定性下降.
迷宫式汽封;气流力;动力特性;数值计算
汽封是汽轮机等透平机械中减少流体泄漏的关键部件.常见的汽封结构有迷宫式[1]、刷式[2]、阶梯式[3]、蜂窝式[4]、指尖式[5]、螺旋槽式[6]和混合式[7]等,而迷宫式汽封在透平机械中最为常见,已得到广泛应用[8].随着机组向大容量和高参数方向发展,汽封气流力对转子稳定性的影响更加显著,汽封中流体周向压力分布不均是引起气流力的主要原因.由于存在偏心,转子在自转的同时还会发生涡动.在转子发生涡动时,转子与汽封之间的间隙会发生周期性变化,进而使其中的流体压力产生周期性脉动,而压力脉动滞后转子位移一个相位角,在与转子偏心方向垂直的方向产生一个加剧转子涡动的激振力,流体形成自激振动[9].然而这种自激振动无法通过动平衡的方法消除[10],轻则影响机组可靠性,重则使机组被迫停机,无法正常运行.汽封流体动力特性是设计时必须考虑的因素之一,以往的研究[11]主要集中在汽封静特性方面.
笔者主要研究了汽封对转子动力特性的影响,采用计算流体力学(CFD)方法建立了迷宫式汽封的三维偏心涡动数值分析模型,对汽封的偏心涡动进行数值模拟,研究了转速、进出口压力比及偏心率对密封动力特性系数和涡动系数的影响,并分析了其对转子动态稳定性的影响.
1 汽封流体动力特性模型
1.1 汽封流体动力特性模型
研究汽封中流体对转子作用力的动力学分析时一般采用线性化模型[12].如图1所示,当转子在静平衡位置受到位移或速度扰动时,气流作用在转子上的气流力会发生变化,当扰动量是微小量时,可将气流力分解为水平和垂直2个分量,即Fx和Fy.

图1 汽封流体动力特性模型
定义刚度系数k为单位位移扰动量引起的气流力增量,阻尼系数c为单位速度扰动量所引起的气流力增量,刚度系数和阻尼系数统称为密封动力特性系数.则动态气流力的矩阵形式为
(1)

假设转子为同心涡动,即涡动中心为静子中心.在同心涡动中,密封腔中静态流动参数沿周向分布均匀,密封动力特性系数中直接刚度系数、阻尼系数项kii、cii(i=x,y)相等,交叉耦合刚度系数、阻尼系数项kij、cij(i=x,y;j=x,y)幅值相等,符号相反,即
则气流力可表示为
(2)
式中:Fr为转子所受径向力,N;Ft为转子所受切向力,N;δ为偏心率,mm;Ω为涡动速度,r/min;K、k分别为直接刚度系数和交叉耦合刚度系数;C、c分别为直接阻尼系数和交叉耦合阻尼系数[13].
转子的稳定性可以用涡动系数来判定,涡动系数的绝对值越小,转子的稳定性越高[14].定义涡动系数Ωf为
(3)
1.2 计算模型
采用前处理软件Gambit来建立模型和划分网格,采用CFD商业软件Ansys Fluent16.0对汽封的流场和气流力进行模拟计算.目前,汽封流体动力特性的CFD计算方法主要包括旋转坐标系法(MRF)和动网格法(Dynamic Mesh).由于汽封间隙较小、流场复杂以及湍流度较大,故采用旋转坐标系法,将非稳态问题转化成稳态问题进行求解,可避免动网格法产生网格变形、畸变的问题,保证了计算结果的准确性.以气流激振实验台中的迷宫式汽封为对象,建立其数值分析模型.图2给出了汽封二维截面示意图.表1给出了汽封各处的尺寸.

图2 汽封二维截面示意图

齿数n齿根间距a/mm齿根厚度b/mm汽封间隙e/mm齿尖宽度d/mm转子半径r/mm汽封半径R/mm4520.50.29097.5
1.3 网格划分及边界条件设置
计算域为汽封通流部分及前后压力进出口,图3为汽封的全三维模型计算域示意图.图4给出了汽封子午面的节点数和网格图.表2给出了子午面及周向各段的网格节点数.因齿顶与转子间隙处的流动变化剧烈,故在此处进行网格的局部细化,经验证网格的进一步细化对计算结果影响不大,即通过了网格无关性检验.最终得到汽封全三维模型的网格节点数约为112万.
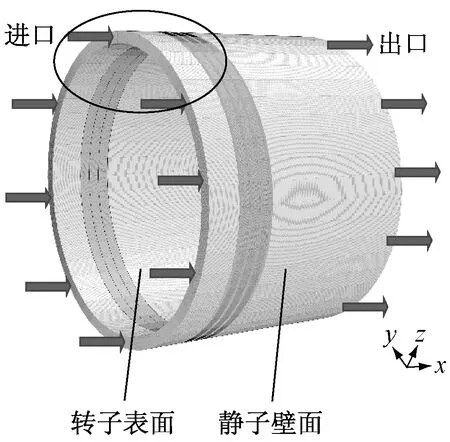


n1n2n3n4周向4050151048
工质为空气,可视为理想气体,采用k-ε湍流模型.进出口边界为压力进出口条件,固定出口压力为1.0×105Pa,通过改变进口压力来模拟不同进出口压力比下的工况条件.壁面均设为绝热边界,气体与壁面采用光滑无滑移边界条件.转子绕其轴心的转速为N,涡动速度为Ω.采用旋转坐标系法(见图5),设置静子壁面的旋转角速度为Ω,转子旋转壁面绕其轴心旋转的相对角速度为N-Ω,汽封壁面绕转子轴心的相对角速度为-Ω.
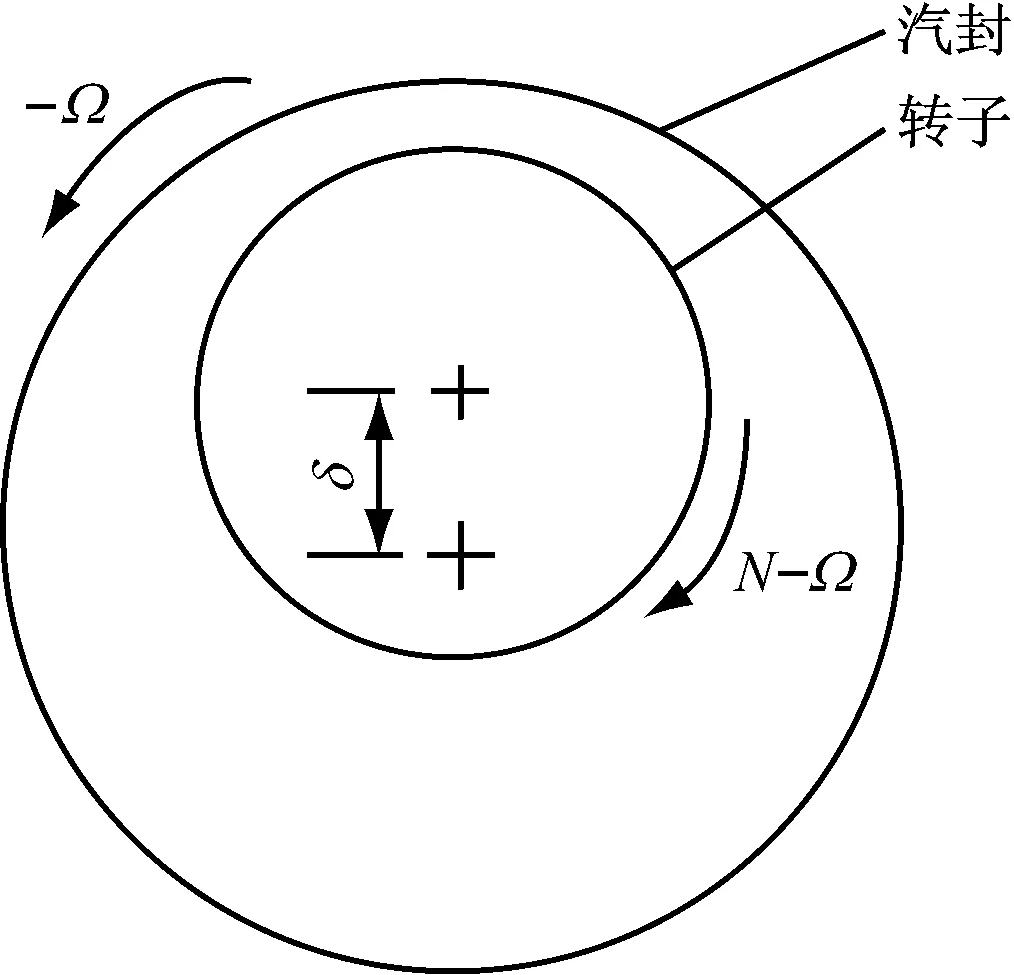
图5 旋转坐标系法
通过控制变量,分别改变不同实验组别的偏心率、进出口压力比、转速和涡动速度来研究汽封流体动力特性的影响因素,从而求出密封动力特性系数.不同实验组别的边界条件设置见表3.

表3 边界条件
2 计算结果与分析
2.1 转速对气流激振特性的影响
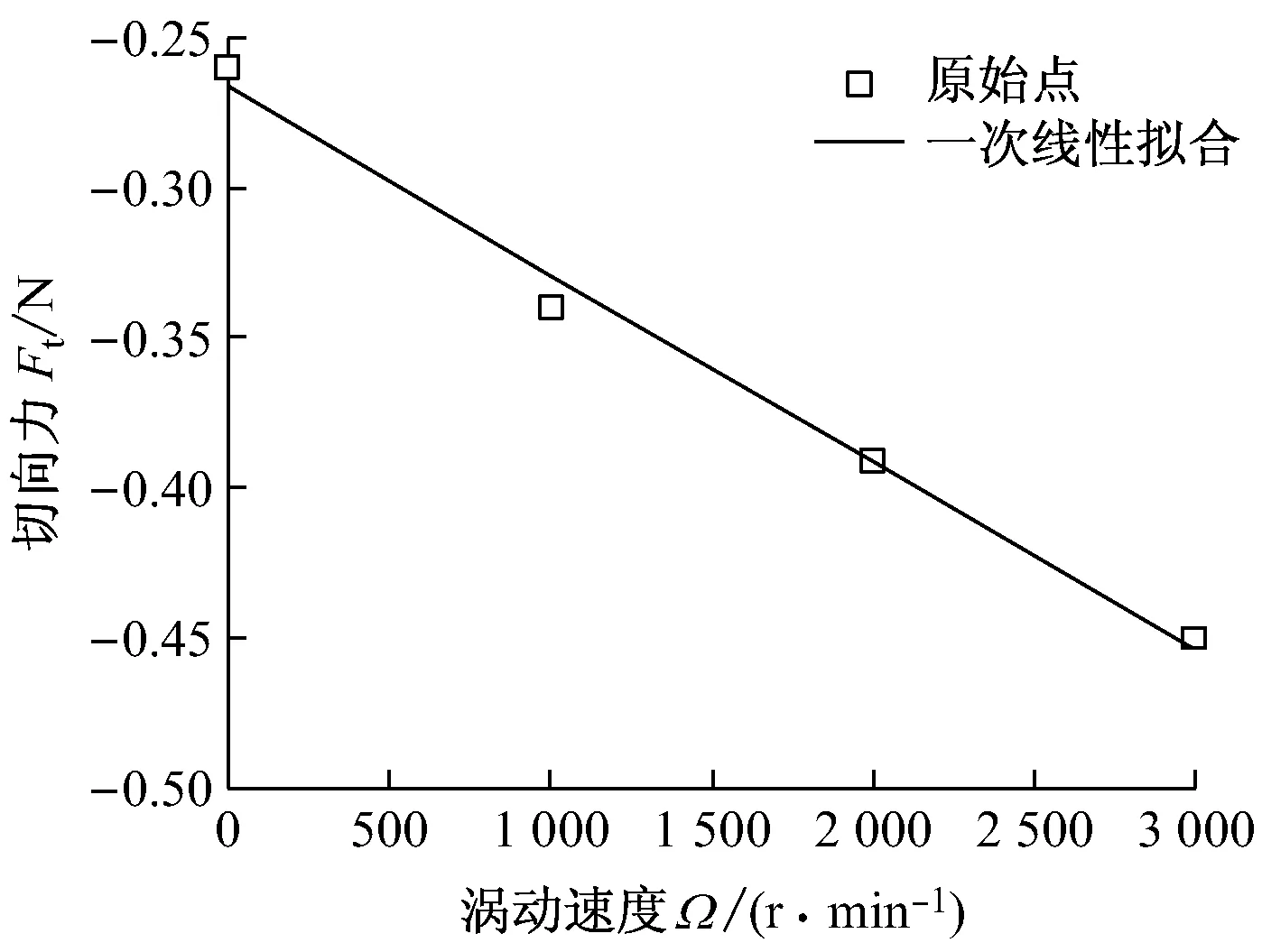
切向力是促使转子涡动的气流力来源,也是导致转子失稳的主要因素.图6给出了不同转速下切向力与涡动速度之间的关系.对图6中的数据进行一次线性拟合,将拟合出的系数代入式(2),求出交叉耦合刚度系数k和直接阻尼系数C,再将其代入式(3)中求出涡动系数.
图7给出了涡动系数随转速的变化.从图7可以看出,随着转速的增大,涡动系数增大,因此转速越高,转子越容易失稳.
2.2 进出口压力比对气流激振特性的影响
图8给出了涡动系数随进出口压力比的变化.从图8可以看出,当转速和偏心率一定时,随着进出口压力比的增大,涡动系数增大,即转子的稳定性随着进出口压力比的增大而下降.
2.3 偏心率对气流激振特性和泄漏量的影响
图9给出了不同偏心率下的涡动系数.从图9可以看出,随着偏心率的增大,涡动系数增大,转子稳定性下降,且与进出口压力比和转速相比,偏心率对转子稳定性的影响更为显著.
在对偏心模型进行计算时,还可以得到不同偏心率下的迷宫式汽封泄漏量,如图10所示.从图10可以看出,当其他条件相同时,泄漏量随着偏心率的增大而增加,但总体增加量不大,在偏心率增大300%的情况下泄漏量只增加了2.1%.
3 结 论
(1) 随着转子转速、进出口压力比和偏心率的增大,涡动系数增大,转子越容易失稳,其中偏心率对转子稳定性的影响更为显著.
(2) 偏心率增大会导致泄漏量增加,汽封的密封效果下降.
(a) N=3 000 r/min

(b) N=6 000 r/min

(c) N=9 000 r/min

(d) N=12 000 r/min

图7 涡动系数随转速的变化

图8 涡动系数随进出口压力比的变化

图9 涡动系数随偏心率的变化

图10 泄漏量随偏心率的变化
[1] 潘永密,郑水英.迷宫密封气流激振及其动力系数的研究[J].振动工程学报,1990,3(2):48-58.
PAN Yongmi,ZHENG Shuiying.Study on the flow induced exciting forces and the dynamic characteristics of labyrinth seals[J].Journal of Vibration Engineering,1990,3(2):48-58.
[2] LELLI D,CHEW J W,COOPER P.Combined three-dimensional fluid dynamics and mechanical modeling of brush seals[J].Journal of Turbomachinery,2006,128(1):188-195.
[3] YÜCEL U.Calculation of leakage and dynamic coefficients of stepped labyrinth gas seals[J].Applied Mathematics and Computation,2004,152(2):521-533.
[4] 张强,何立东.蜂窝密封动力特性系数的计算方法[J].中国电机工程学报,2007,27(11):98-102.
ZHANG Qiang,HE Lidong.Study on calculation of the dynamic coefficients of honeycomb seals[J].Proceedings of the CSEE,2007,27(11):98-102.
[5] 苏华.指尖密封结构和性能的设计分析与试验研究[D].西安:西北工业大学,2006.
[6] CHILDS D W,GANSLE A J.Experimental leakage and rotordynamic results for helically grooved annular gas seals[J].Journal of Engineering for Gas Turbines and Power,1996,118(2):389-393.
[7] LAOS H E,VANCE J M,BUCHANAN S E.Hybrid brush pocket damper seals for turbomachinery[J].Journal of Engineering for Gas Turbines and Power,2000,122(2):330-336.
[8] 何立东,袁新,尹新.刷式密封研究的进展[J].中国电机工程学报,2001,21(12):28-32,53.
HE Lidong,YUAN Xin,YIN Xin.The advance in the investegation of brush seal[J].Proceedings of the CSEE,2001,21(12):28-32,53.
[9] 徐悦,田爱梅.基于CFD的涡轮泵转子密封流体激振研究进展[J].火箭推进,2005,31(1):8-13.
XU Yue,TIAN Aimei.Progress of investigation on turbopump annular seal fluid-induced vibration based on CFD[J].Journal of Rocket Propulsion,2005,31(1):8-13.
[10] 沈耀阳.迷宫密封气流激振的数值模拟与分析[D].保定:华北电力大学,2008.
[11] 骆名文,丁学俊,祁小波,等.大型汽轮机汽流激振研究现状及展望[J].热能动力工程,2006,21(6):551-555.
LUO Mingwen,DING Xuejun,QI Xiaobo,et al.The status quo and prospect concerning a study on steam flow excitations in large-sized steam turbines[J].Journal of Engineering for Thermal Energy and Power,2006,21(6):551-555.
[12] 张万福.汽轮机流体激振及抑制技术理论与试验研究[D].南京:东南大学,2013:41-43.
[13] HIRANO T,GUO Zenglin,KIRK R G.Application of computational fluid dynamics analysis for rotating machinery-part II:labyrinth seal analysis[J].Journal of Engineering for Gas Turbines and Power,2005,127(4):820-826.
[14] CHILDS D.Turbomachinery rotordynamics:phenomena,modeling,and analysis[M].New York,USA:Wiley,1993.
Research on Flow Field Dynamic Characteristics in a Labyrinth Seal
MAHaoyuan1,ZHANGWanfu1,2
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering,School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
A full three-dimensional model was set up for a labyrinth seal,in which the flow field was calculated and analyzed under different working conditions using commercial CFD software Fluent,so as to study the relations of the fluid-induced force with the rotational speed,pressure ratio and the eccentricity,etc.,and to obtain the dynamic coefficient and whirl coefficient of the seal that may influence the stability of the rotor.Results show that with the rise of rotational speed,pressure ratio and eccentricity,the whirl coefficient increases accordingly,and the stability of the rotor is hence reduced.
labyrinth seal; fluid-induced force; dynamic characteristic; numerical simulation
2016-03-11
2016-04-18
国家自然科学基金资助项目(11402148)
马浩原(1995-),男,满族,河北承德人,本科,研究方向为动力机械强度与振动.张万福(通信作者),男,讲师,博士,电话(Tel.):18817882508;E-mail:wfzhang@usst.edu.cn.
1674-7607(2017)01-0021-05
TK263
A 学科分类号:470.30
