微机械轮式角振动陀螺气体阻尼特性研究*

陈奥运,凤 瑞,庄须叶,徐大诚*,郭述文,

(1.苏州大学微纳传感技术研究中心,江苏 苏州 215100;2.北方通用电子集团有限公司,江苏 苏州 215163)

微机械轮式角振动陀螺气体阻尼特性研究*

陈奥运1,凤 瑞2,庄须叶2,徐大诚1*,郭述文1,2

(1.苏州大学微纳传感技术研究中心,江苏 苏州 215100;2.北方通用电子集团有限公司,江苏 苏州 215163)

轮式角振动陀螺气体阻尼效应是影响其动态特性的主要因素。在充分研究轮式角振动陀螺结构特征的基础上,创建了角振动陀螺驱动模态滑膜阻尼数学解析模型,并给出了改进解析模型。利用有限差分算法求解极坐标系下雷诺方程,建立了敏感模态压膜阻尼简化分析模型。在5 Pa到105Pa压强范围内,进行了简化分析模型计算,同时对计算结果进行了与ANSYS 仿真结果的比对。理论模型计算与仿真结果表明,敏感模态压膜阻尼是轮式角振动陀螺气体阻尼的主要产生机制。进而,从结构设计和控制电路的角度,给出了减小气体阻尼效应的有效方法。

微机械轮式角振动陀螺;滑膜阻尼;压膜阻尼;品质因数

微机械陀螺是基于哥式效应测量目标物旋转角度或角速度的传感器[1-2]。该类陀螺一般处于谐振工作状态,谐振性能的优劣直接决定着测量精度的高低。而表征谐振器性能的重要参数之一是Q值。对于硅微材料的谐振器而言,决定其Q值大小的因素主要有真空度、锚点结构和材料热特性等方面[3-7]。乔治亚理工Jacob等[8]通过求解三维Stokes方程,给出了硅微横向谐振器气体阻尼解析结果;纽约州立大学Dorel等[9]分析了用于陀螺、加速度计等硅微器件的带孔结构的气体阻尼;东南大学苏岩等[10]给出了轮式角振动陀螺粘性滑膜阻尼数学模型。综合以上文献,虽然对该类陀螺气体阻尼特性分析进行了部分研究,但比较系统的分析气体阻尼对Q值影响还未见报道。

本文以轮式角振动陀螺为研究对象,在文献[10]的基础上,改进了低真空度下驱动模态滑膜阻尼数学解析模型。建立了敏感模态滑膜阻尼解析模型,并与有限元分析结果作对比验证。进而比较全面的给出了气体阻尼对Q值影响的分析方法。压膜阻尼解析结果与有限元分析结果接近,且在相同条件下远大于滑膜阻尼,是形成气体阻尼的主要因素。

1 轮式角振动陀螺结构

图1为轮式角振动陀螺结构示意图,其驱动轴为z轴,y轴为敏感检测轴,角速率输入轴为x轴。振动质量块通过4个弯曲梁连接至内环,内环由两扭转梁与中心锚点连接。此种结构的振动质量块耦合了驱动和检测两模态的运动,拥有较高的灵敏度。陀螺通过静电梳齿驱动方式作平面内振动,当有角速度输入时,科氏力矩激励质量块绕y轴产生振动。质量块下方对称分布的两差分电容用以敏感该振动信号,通过C-V转换、解调后得到角速度信号。

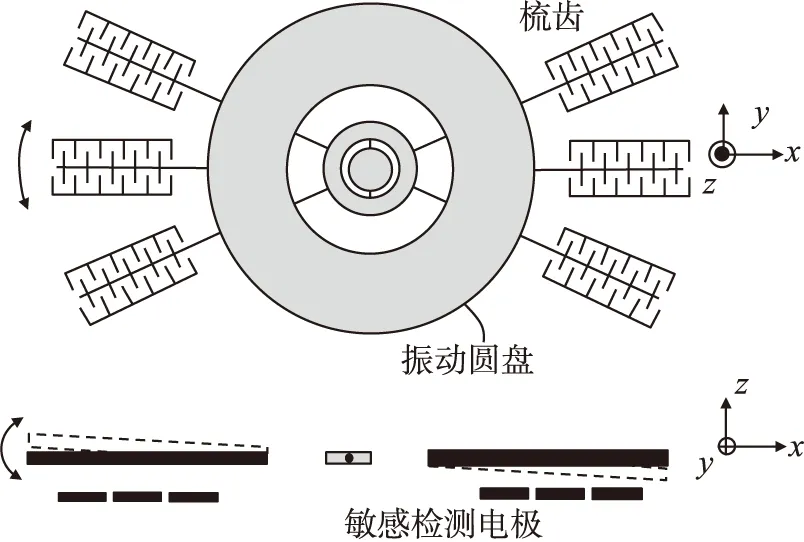
图1 轮式角振动陀螺结构示意图

陀螺结构为层厚度30 μm,质量块与检测电极间隙1.6 μm。详细尺寸如表1所示。

表1 轮式角振动陀螺尺寸

2 气体阻尼理论

2.1 气体阻尼流场模型

Knudsen(M.H.C,1871—1949)提出了努森数的概念,阐述了气体的平均自由程与特征尺寸之比的重要意义,表示为

Kn=λ/d

(1)式中:λ为气体分子平均自由程,d为器件的特征尺寸。

在MEMS器件的气体阻尼分析中,依据努森数可区分不同特性的流动区域,Kn≤0.01、0.0110的气流分别为连续流区、滑移流区、过渡流区、自由分子流区[11]。

流体阻尼源自流体自身的粘性,表示为流体的剪切力与流速梯度的比例因子-粘滞系数μ,常温常压下μ=1.78×10-5Pa·s。

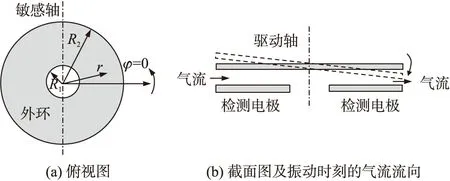
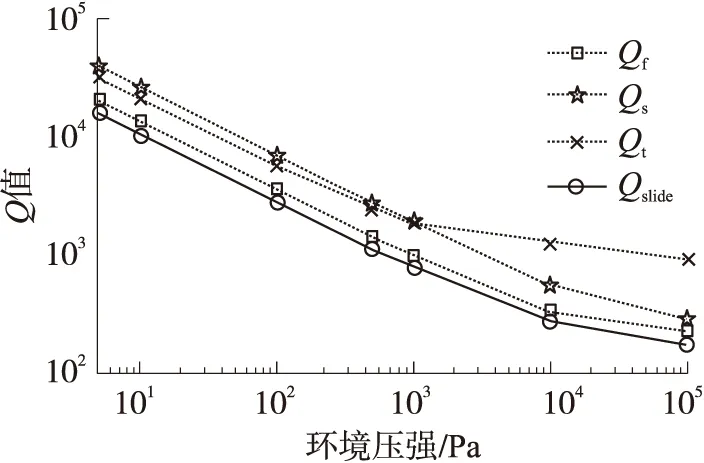
当0.01

(2)

2.2 滑膜阻尼

驱动模态的滑膜阻尼主要有3个部分:质量块与下衬底之间、质量块动齿与定齿侧壁之间和质量块与上硅盖帽之间的滑膜阻尼。梳齿间距df和质量块与下电极间隙ds通常远小于δ,应采用Couette流模型计算;质量块与硅盖帽之间距离较大,应采用Stokes流模型较精确。本文计入了质量块与上硅盖帽之间的滑膜阻尼,源于驱动模态滑膜阻尼的Q值计算结果较文献[10]更加精确。沿用文献[6]的推导方法可得:

源于弧形梳齿之间滑膜阻尼的Qf

(3)

式中:IZ为驱动模态转动惯量,ω为振荡频率,df为梳齿间距,Ri为第i个可动弧形梳齿到驱动轴距离,Ai为第i个动齿的阻尼面积。

源于质量块与下电极之间的滑膜阻尼Qs

(4)

式中:ρp、t分别为质量块的密度和厚度。

源于质量块与硅盖帽之间的滑膜阻尼Qt

(5)

当流体处于非连续流时,μ由μeff校正。因此,驱动模态滑膜阻尼导致的QSlide可由下式计算。

(6)

2.3 压膜阻尼

雷诺方程对连续流流体有较好描述,通过有效粘滞系数的校正,雷诺方程的应用范围可扩展至滑移流、过渡流、自由分子流[12]。忽略温度变化和空气压缩,极坐标系下的雷诺方程可表示为[14]

(7)

式中:P包含环境压强Pa和压膜阻尼产生的阻尼压力p,即P=Pa+p,dh/dt表示气体薄膜厚度变化率。

由于敏感模态质量块绕敏感轴扭动,在r向和φ向均有压力梯度存在,因此直接求解雷诺方程较为复杂。本文采用有限差分法求解压力分布。若计入梳齿与谐振梁,计算量庞大,且敏感模态压膜阻尼主要产生于外环与检测电极之间。综合考虑可将模型简化为环形极板与检测电极之间压膜阻尼的计算。简化模型如图2所示。图中标出了φ=0的起始位置。本文所研究陀螺工作频率远低于临界频率,压膜刚度效应可忽略不计[15]。

图2 压膜阻尼简化计算模型

将简化模型进行等分网格化,每个格点的压强用Pi,j表示,下标i和j分别表示沿r向和φ向的网格,Δr、Δφ表示r向和φ向的格点间距。则极坐标系下的雷诺方程的中心差分格式为

(8)

可以推得压力分布的迭代格式为

(9)

在硅微角振动陀螺开环工作模式下,质量块绕敏感轴最大扭转角θmax=0.001 6rad,扭转角很小,可取tanθ≈sinθ≈θ,则质量块与下电极间距h可表示为

h=h0±rcosφtanθ≈h0±(rcosφ)θ

(10)

因此

(11)

边界条件为:r=R1或R2时,P=Pa。φ=π/2或3π/2时,∂P/∂r=0,Pa为环境压强。

网格单元中心到敏感轴的距离为

(12)

每个网格单元的面积为

(13)

一个网格单元的平均压强差为

(14)

式中:ΔPi,j表示第(i,j)个网格左右两个侧面的压强差。因此,振动质量块阻尼合力矩为

(15)

式中:ni、nj分别为r向和φ向的网格总数。从而阻尼系数

(16)

压膜阻尼导致的角振动的谐振结构损耗因子由压膜阻尼系数C,敏感模态弹性系数K及等效转动惯量J共同决定[16],即

(17)

因此,敏感模态压膜阻尼损耗导致的QSqueeze

(18)

3 计算与仿真结果分析

3.1 滑膜阻尼计算

本文所研究的轮式角振动微机械陀螺驱动模态谐振频率fd=10 kHz,驱动模态转动惯量的大小IZ=3.52×10-14kg·m2。在室温(25 ℃)下,改变真空度,计算滑膜阻尼损耗导致的Q值。压强的降低应保证努森数Kn<880。求得滑膜阻尼Q值与压强关系如图3所示。

图3 室温(25 ℃)下驱动模态滑膜阻尼Q值与压强关系

由以上计算结果可以看出,轮式角振动陀螺源于驱动模态滑膜阻尼的Q值随压强增大而减小。实验测得5Pa环境压强下驱动模态的滑膜阻尼的Q值为29 973,解析模型计算值为25 416,两者结果接近,证明了解析模型的正确性。另外,从图3可以看出,Qt与Qf及Qs数值相当,因此振动质量块与硅盖帽之间的滑膜阻尼不可忽略,是构成驱动模态滑膜阻尼的重要组成部分。

3.2 压膜阻尼解析模型验证

利用MATLAB计算基于雷诺方程有限差分算法的敏感模态压膜阻尼Q值,并将结果与ANSYS环境下的仿真结果进行比较验证。在使用ANSYS进行压膜阻尼分析时,先使用SHELL93单元进行模态分析,利用模态分析得出的每个节点的位移信息,进而利用FLUID136单元算出压强分布。在此基础上采用模态投影法计算模态阻尼比和Q值。解析计算中,取Δr=1μm,Δφ=0.1°。敏感模态等效转动惯量Iy=2.13×10-14kg·m2,敏感模态谐振频率fs=10.358kHz,特征尺寸d=1.6μm。部分压强值下解析模型所得Q值与ANSYS仿真所得Q值如表2所示,5Pa到105Pa范围内两者结果对比如图4所示。

图4 解析结果与ANSYS仿真结果对比

压强/Pa5101102103104105解析值7230346324418.71.720.31ANSYS6020278020816.11.490.28

由图4可以看出,基于雷诺方程,利用简化模型所求得的Q值解析结果与ANSYS仿真结果非常接近,从而验证了解析模型的正确性。由于简化模型未计入梳齿与检测电极之间压膜阻尼,因此计算结果略大于ANSYS仿真结果。

对比滑膜阻尼和压膜阻尼的计算结果可以看出,相同条件下,源于滑膜阻尼的Q值比源于压膜阻尼的Q值大2到3个数量级。因此,敏感模态压膜阻尼是形成气体阻尼的主要来源。由于敏感检测电容较小,考虑到检测灵敏度,未对检测极板做开孔处理以减小压膜阻尼。

图5给出了室温下,5 Pa环境压强的敏感模态压膜阻尼压力分布云图,可以看出压力分布梯度主要集中在敏感轴两侧的外环质量块下方,梳齿及内环下方压强改变并不明显,从而说明了简化模型建立的可行性。

图5 敏感模态压力分布云图

4 结论

本文分析和仿真了微机械轮式陀螺谐振模态的滑膜阻尼效应和敏感模态的压膜阻尼效应,给出了压膜阻尼的简化解析模型,并在此基础上改进了滑膜阻尼的解析模型。模型解析结果与有限元分析结果进行了对比验证,两者结果具有良好的一致性。在分析两种模态气体阻尼效应模型基础上,也分析总结出了角振动陀螺开环工作模式下的压膜阻尼是影响其动态特性的主要因素,还可以采用敏感闭环控制电路抑制振幅来减小压膜阻尼的影响。

[1] Guo Zhanshe,Cheng Fucheng,Li Boyu,et al. Research Development of Silicon MEMS Gyroscopes:A Review[J]. Microsystem Technologies,2015,21(10):2053-2066.

[2] 刘梅,周百令,夏敦柱. 对称解耦硅微陀螺仪结构设计研究[J]. 传感技术学报,2008,21(3):435-438.

[3] 高嵘,王小静,张效翔,等. 计入空气阻尼的MEMS微谐振器非线性动力学研究[J]. 传感技术学报,2006,19(5):1354-1357.

[4] Gologanu M,Bostan C G,Avramescu V,et al. Damping Effects in MEMS Resonators[C]//2012 International Semiconductor Conference,2012,1:67-76.

[5] 周镇威,杨卓青,蔡豪刚,等. 带有凸条平板的MEMS结构压膜阻尼效应分析[J]. 传感技术学报,2010,23(5):665-669.

[6] Ekeom D. Thermal-Electromechanical FEM-BEM Model for MEMS Resonator Simulation[J]. Journal of Microelectromechanical Systems,2011,20(1):184-192.

[7] Ha T D,Bao J F. Reducing Anchor Loss in Thin-Film Aluminum Nitride-on-Diamond Contour Mode MEMS Resonators with Support Tethers Based on Phononic Crystal Strip and Reflector[J]. Microsystem Technologies,2016,22(4):791-800.

[8] Ye W,Wang X,Hemmert W,et al. Air Damping in Laterally Oscillating Microresonators:A Numerical and Experimental Study[J]. Journal of Microelectromechanical Systems,2003,12(5):557-566.

[9] Homentcovschi D,Bruce T,Murray B T,et al. Viscous Damping and Spring Force Calculation of Regularly Perforated MEMS Microstructures in the Stokes’ Approximation[J]. Sensors and Actuators A Physical,2013,201:281-288.

[10] 裘安萍,苏岩. 振动轮式微机械陀螺仪中滑膜阻尼机理的研究[J]. 中国机械工程,2006,17(16):1679-1682.

[11] Rostami A A,Mujumdar A S,Saniei N. Flow and Heat Transfer for Gas Flowing in Microchannels:A Review[J]. Heat and Mass Transfer,2002,38(4/5):359-367.

[12] Veijola T,Kuisma H,Lahdenpera J,et al. Equivalent-Circuit Model of the Squeezed Gas Film in a Silicon Accelerometer[J]. Sensors and Actuators A:Physical,1995,48(3):239-248.

[13] 白晓晓,李梦委,储伟航,等. 谐振式微陀螺中通孔质量块阻尼建模研究[J]. 中北大学学报,2015,36(3):366-371.

[14] Beschorner K,Higgs C F,Lovell M. Solution of Reynolds Equation in Polar Coordinates Applicable to Nonsymmetric Entrainment Velocities[J]. Journal of Tribology,2009,131(3):034501.

[15] 张雄星,王伟,彭首军. MEMS器件平板运动结构的空气阻尼分析[J]. 西安工业大学报,2010,30(4):310-314.

[16] Pandey A K,Pratap R. A Semi-Analytical Model for Squeeze-Film Damping Including Rarefaction in a MEMS Torsion Mirror with Complex Geometry[J]. Journal of Micromechanics and Microengineering,2008,18(10):1270-1282.

Research on Air Damping of Micro-Machined Wheel Angular Vibration Gyroscope*

CHENAoyun1,FENGRui2,ZHUANGXuye2,XUDacheng1*,GUOShuwen2

(1.Micro-Nano Sensor Technology Research Center,Soochow University,Suzhou Jiangsu 215100,China;2.North General Electronics Group Co.,Ltd,Suzhou Jiangsu 215163,China)

The air damping of Micro-machined Wheel Angular Vibration Gyroscope is a main factor to influence the dynamic performance. A physical model is proposed and improved for the characterization of the slide film damping of drive mode based on adequate studies of the whole structure. A simplified model to calculate the squeeze film damping of sense mode is given by solving the Reynolds equation through the finite-difference method. The formulation is calculated in the 5 Pa～105Pa range of pressure change,and the model is validated by comparing with the ANSYS results. The theoretical model computation and simulation results all shows that the squeeze film damping of sense mode is the main generation mechanism of the whole air damping in wheel angular vibration gyroscope. Effective ways to reduce the air damping effect is given from the perspective of structure design and circuit control.

micro-machined wheel angular vibration gyroscope;slide film damping;squeeze film damping;quality factor

陈奥运(1992-),男,汉族,硕士研究生,主要研究方向为硅微陀螺能量耗散机理分析,cayemail@163.com;徐大诚(1963-),男,汉族,教授,主要研究方向为MEMS传感器信号处理技术研究,xudacheng@suda.edu.cn; 郭述文(1955-),男,汉族,苏州大学电子信息学院特聘教授,主要研究方向为MEMS传感器设计与开发研究,shuwenguo@wzxmems.com。

项目来源:国家自然基金重点项目(61434003);装备预研基金项目(9140A09032015)

2016-05-17 修改日期:2016-07-24

U666.12

A

1004-1699(2017)01-0054-05

C:2575

10.3969/j.issn.1004-1699.2017.01.011