采用SVD-NMF的管道泄漏信号去噪算法
2017-02-07肖启阳
肖 楠,李 健,肖启阳
(天津大学 精密测试技术与仪器国家重点实验室,天津300072)
采用SVD-NMF的管道泄漏信号去噪算法
肖 楠,李 健*,肖启阳
(天津大学 精密测试技术与仪器国家重点实验室,天津300072)
在管道泄漏检测中,压力信号中的噪声干扰会降低传统互相关法的定位精度。传统的去噪算法对环境的适应性差,去噪效果不理想。为此,提出了一种奇异值分解SVD(Singular Value Decomposition)与非负矩阵分解NMF(Nonnegative Matrix Factorization)相结合的管道泄漏信号去噪算法。该方法首先通过奇异值分解确定非负矩阵分解的阶数并对其初始化;然后,采用改进的非负矩阵分解算法对原信号进行迭代分解,获得去噪信号;最后,对去噪信号进行处理后通过互相关计算时延,并结合泄漏信号的传播速度实现泄漏定位。大量实验结果表明,SVD-NMF算法能够显著降低迭代次数,提高去噪速度;同时在泄漏检测中,能够达到去除噪声干扰,提高定位精度的目的。
管道泄漏定位;非负矩阵分解(NMF);奇异值分解(SVD);互相关;负压波
管道运输已成为现代工业和国民经济的命脉,在运输气体、液体等方面具有重要作用。随着管网的迅速发展,由于管道老化、腐蚀、第三方破坏等原因导致的泄漏事故频繁发生,造成资源浪费和环境污染的同时,也存在着安全隐患。因此,对管道泄漏进行精确定位具有重要意义[1-2]。
基于负压波的泄漏检测法由于其施工量小、成本低、维护方便、检测距离远等优点,在国内外长输管道泄漏检测领域获得广泛应用[3-4]。然而传感器采集的实际信号中包含噪声,导致时延计算不准确,降低泄漏定位精度。因此,增强泄漏信号,抑制压力信号中的噪声,提高信噪比,成为精确判断和定位泄漏的关键。目前,负压波信号处理技术存在两大难题:负压波信号的微弱性和干扰噪声的多样性[5],因此需采用合适的算法去除噪声干扰。
近年来,针对管道压力信号去噪,国内外学者进行了许多研究:2007年,路炜[6]等利用信号的互谱相位谱和相关系数估计泄漏信号的频率范围,对信号进行滤波,提高信噪比;2012年,文玉梅[7]等根据不同带宽信号与噪声自相关长度的差异,对检测信号中的窄带噪声和宽带噪声进行自适应抑制;2013年,赵利强[8]等采用改进的EMD算法对泄漏信号的特征进行提取,实现管道泄漏检测;同年,文玉梅[9]等利用泄漏信号源和固定干扰源之间的独立性,采用盲卷源分离算法将干扰源进行分离,保留了泄漏信号中的时延信息;2014年,孙洁娣[10]等采用局域均值分解对信号进行处理,结合峭度特征重构信号在进行互相关定位;同年,Ostapkowicz[11]等采用中值滤波和短时互相关算法,通过阈值检测进行定位;2015年,Mostafapour[12]等通过小波分析和模型定位理论,对泄漏信号的低频和高频部分分别进行小波分解来去除噪声;同年,梁伟[13]等采用双树复小波变换和奇异值分解进行信号去噪对泄漏进行精确定位。
基于非负矩阵分解的去噪算法是近年来兴起的去噪方法,其得到的去噪信号不存在相移,非常适合用于泄漏定位前的预处理算法。然而非负矩阵分解的阶数及矩阵的初始化的不确定性会造成算法的去噪效果差,收敛时间长。因此,本文将奇异值分解与非负矩阵分解结合,以奇异值差分谱的峰值位置作为非负矩阵分解的阶数并初始化,对管道压力信号进行处理,最后通过加权残差和互相关分析对泄漏进行检测定位。实验结果表明,采用结合奇异值分解的非负矩阵分解算法,收敛速度更快,去噪效果更好,定位精度也更高。
1 非负矩阵分解降噪算法
非负矩阵分解NMF(Non-Negative Matrix Factorization)是由Lee和Seung等人于1999年提出,并发表在Nature杂志上的一种新的矩阵分解方法[14],广泛应用于图像分析、数据挖掘、语音处理等领域。近年来,学者在原NMF算法的基础上进行修改,取得了不少成果[15-19]。NMF算法的优点在于:由于其要求矩阵元素为非负,因此其分解形式和结果有很强的解释性;其次,矩阵分解后的结果一般具有自然的稀疏性,不但易于表示,占用空间也相应缩小。由于管道压力信号的值为正值,采用非负矩阵分解对压力数据进行处理满足算法的要求。
1.1 非负矩阵分解
非负矩阵分解算法可以这样定义:给定一个非负矩阵X∈Rm×n,将矩阵X分解成为W∈Rm×d和H∈Rd×n两个非负矩阵的乘积,即:
X+≈W+H+
(1)
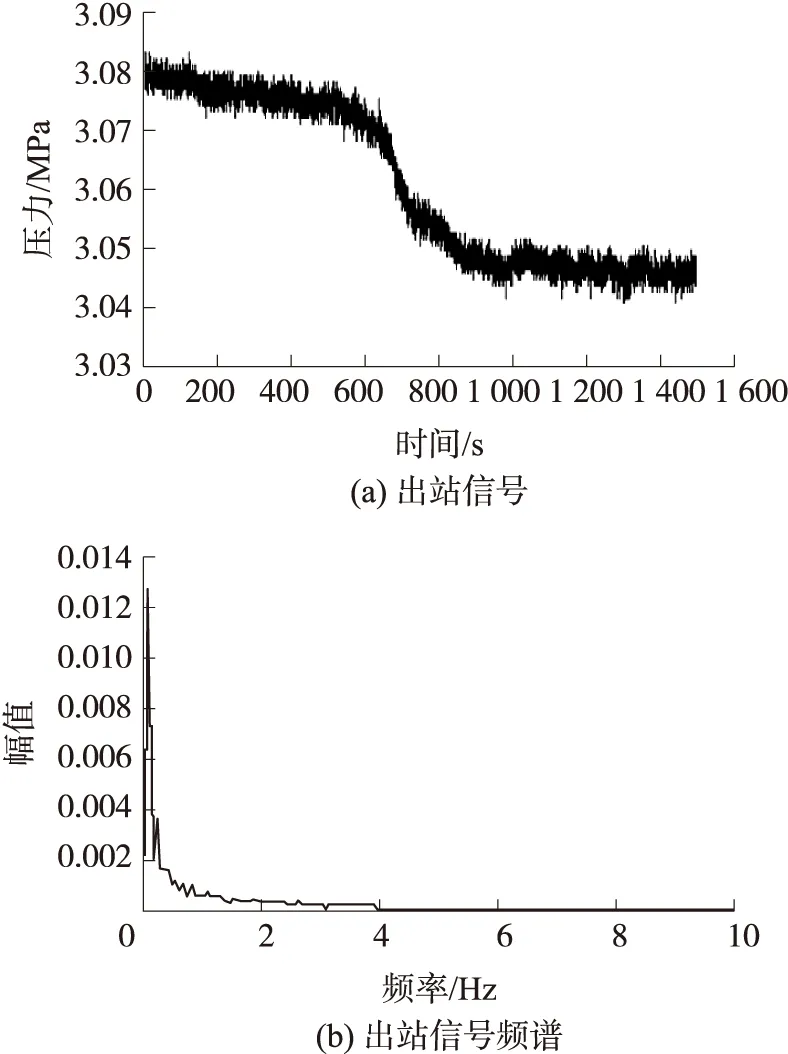
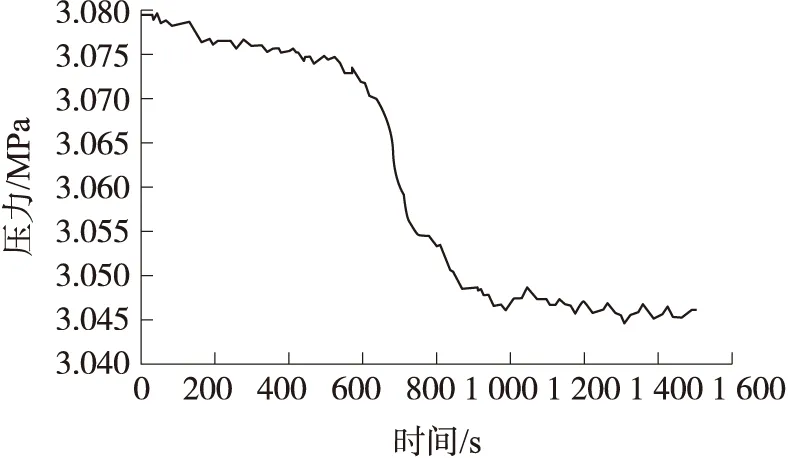
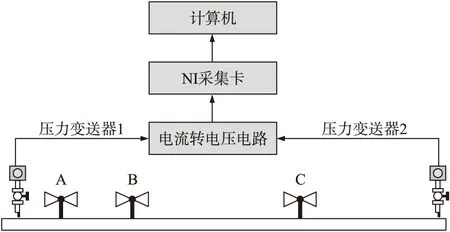
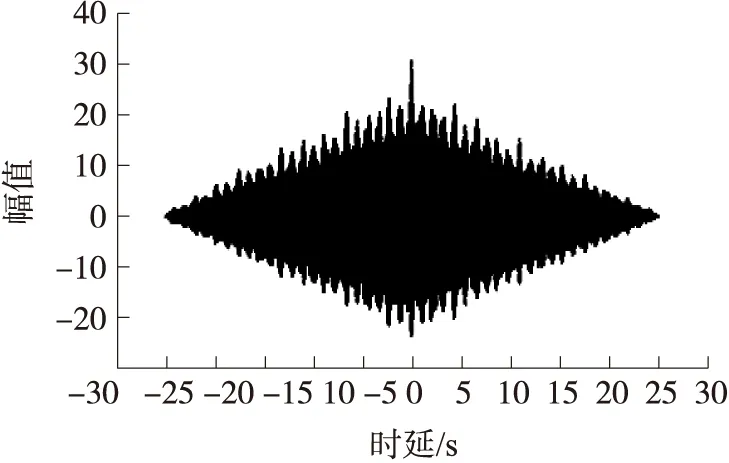
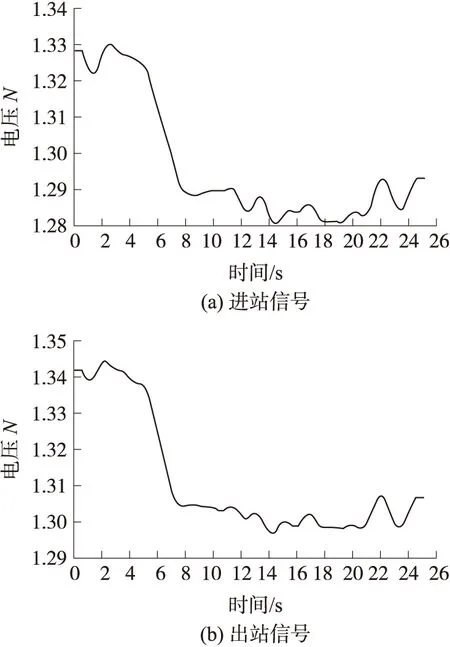
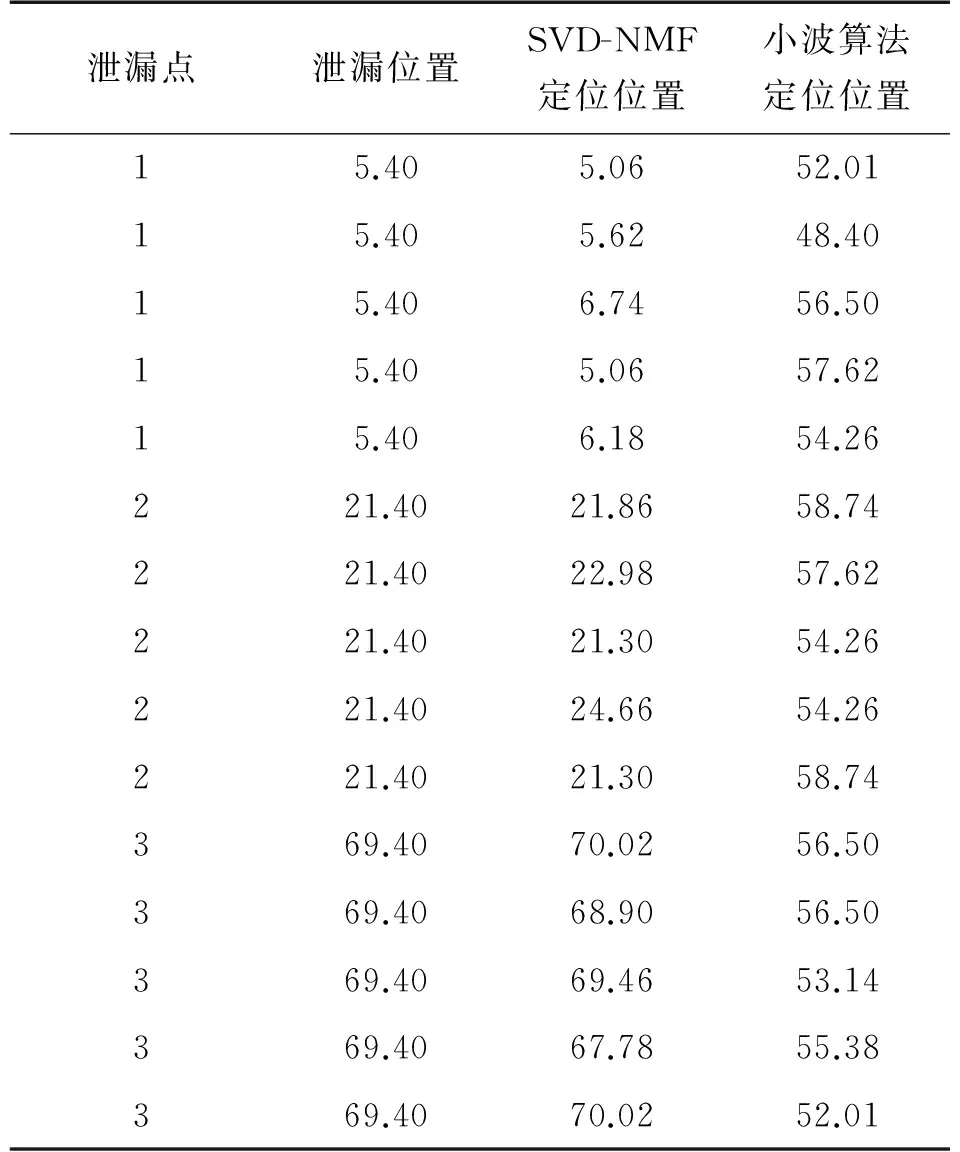
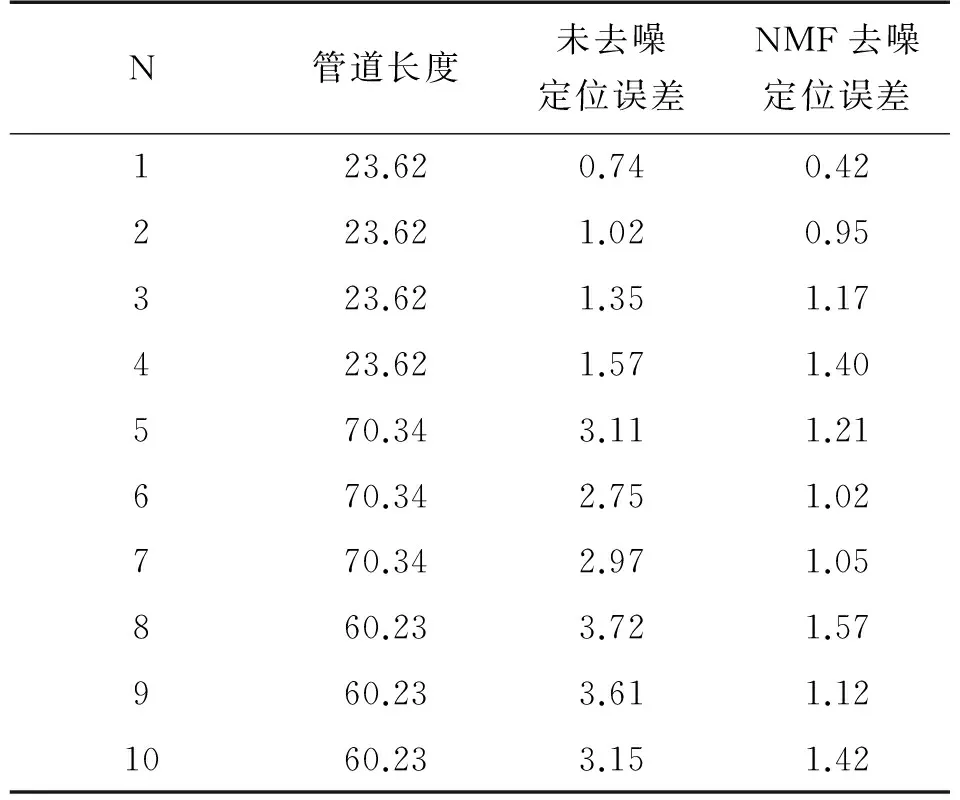
式中:下标“+”代表非负约束,参数d为近似描述原始数据的低维空间维度,应满足(m+n)d 对于式(1)的求解要求矩阵W和H的乘积与原矩阵X逐步逼近,通常采用欧氏距离来表征两者间的误差,误差函数为: (2) 式中:矩阵X,W,H的元素为非负。当上式取得最小值时,矩阵X与矩阵W和H的积误差最小。Lee和Seung给出了对应上式的迭代规则: (3) (4) 根据以上两式进行迭代,当W和H收敛时,迭代结束,非负矩阵分解完成。 1.2 奇异值分解 奇异值分解是线性代数中的一种重要的矩阵分解,其数学表达式为:给定一个矩阵X∈Rm×n,存在一个分解使得: X=USVT (5) 式中:U∈Rm×m,V∈Rn×n为正交矩阵,S为对角矩阵,对角线元素s1,s2,…,sq为矩阵X的奇异值,并满足s1≥s2≥…≥sq>0。在信号处理应用中,通常会出现: s1≥s2≥…≥sk≫sk+1≥…≥sq (6) 的情况,即前k个奇异值远远大于后q-k个奇异值,可以认为前k个奇异值代表着有用信号,而后q-k个奇异值对应噪声信号。因此,我们可以选取前k个奇异值作为有效奇异值,并将其他奇异值置零,而后将其作为新的矩阵S与矩阵U和V相乘,得到处理后的新矩阵[20-21]。 在使用奇异值分解进行信号处理中,需要将一维信号构造为二维Hankel矩阵。设一维离散信号k={k(i)},i=1,2,…,N,采用滑动窗口截取的方式来获取多个行向量,得到矩阵X: (7) 之后对矩阵X进行奇异值分解,选取前k个奇异值保留后进行重构,反复迭代几次就可以对原信号进行去噪。 对于有效奇异值数的选取,通常采用奇异值差分谱的方法进行,差分谱的定义为: Δsk=sk-sk+1 (8) 可以看出,当相邻两奇异值相差较大,则会在差分谱序列中产生一个峰值,相当于式(6)中的突变位置k。通过差分谱的计算就可以实现有效奇异值个数的自适应选取[22]。 1.3 SVD-NMF降噪算法 在1.1节中介绍的非负矩阵分解基础算法中,由于只存在矩阵非负这一个约束条件,造成其在对图像、信号等较为复杂的数据进行处理时,迭代往往无法收敛,造成算法失效。为了解决这一问题,许多学者也在原算法基础上添加其他的约束以提高分解矩阵的可解释性。比较典型的就是Hoyer提出的NMFSC算法[23],该算法以非线性投影的方式实现精确控制结果的稀疏性。 大部分对NMF算法进行的改进都是在原有的算法上添加其他条件来改变算法迭代公式,从而提高算法的稀疏度等要求,而少有针对NMF算法本身来提高算法效果的方法。在1.1节介绍的基础算法中,参数d以及矩阵W和H的初始化均是不定的,而d的取值也会影响矩阵W和H的大小。可以想象,对参数d以及矩阵W和H的不同取值会严重影响算法的迭代结果,甚至无法收敛,造成算法失效。因此,需要对参数d以及矩阵W和H的初始化进行确定,以保证算法的可靠性。 由于参数d表示近似描述原始数据的低维空间维度,即原信号中占绝大部分比重的有效信号,而这与奇异值分解中有效奇异值的个数所代表的有用信号相一致。因此,我们可以采用奇异值分解得到的有用信号数目来确定参数d,以完整保存有用的信号。同时,选取奇异值分解中矩阵U和V的前k行(列)作为W和H的初始化矩阵,以达到快速收敛的目的。 图1 原信号 为验证算法的可行性,我们选取一段实际管道泄漏信号进行去噪,其波形如图1(a)所示。将直流部分滤除掉,对应的频谱如图1(b)所示。从图1(b)中可以看出,噪声多分布于低频部分,与有用信号频率重叠,通过传统频域滤波的方式进行降噪无法得到满意的效果。 将信号进行直接NMF降噪,分别选择参数d为1、2、3,以展示不同参数d的取值对NMF算法降噪的影响,同时设置迭代超过100次停止,矩阵W和H为随机初始化,降噪结果如图2所示。 图2 NMF处理后的信号 从图2可以看出,当参数d取1时,处理后的信号较为平滑,可以认为满足降噪要求;当参数d取2时,处理后的信号中仍存在较大的毛刺;而参数d取3时,处理后的信号中的毛刺更大,影响压力下降位置的判断。在这3次实验中,迭代次数均达到了100次,证明矩阵W和H初始化随机,造成算法收敛过慢,运算时间过长。 采用SVD-NMF算法进行降噪的结果如图3所示。结果表明,处理后的信号基本上去除了噪声,波形较为平坦,同时迭代次数为3,证明SVD-NMF算法能够快速收敛,缩短计算时间。 图3 SVD-NMF处理后的信号 2.1 管道泄漏定位原理 管道泄漏定位原理图如图4所示,在管段两端分别设置有两个传感器,当管段中间产生泄漏时,泄漏信号到达首尾两端传感器的时间差为Δt,设泄漏信号的传播速度为v,两传感器间的距离为D,则首端传感器与泄漏点之间的距离d表示为: (9) 式中:信号的传播速度v可以通过实际测量得到,而传感器间距D也容易得出,因此上时间差Δt就成为影响定位精度的关键因素。 确定时间差Δt的方法是计算互相关函数。对于两个离散信号x(N)和y(N),两者的互相关函数表达式为: (10) 式中:m从 0到N-1变化。 图4 泄漏原理示意图 2.2 改进的互相关定位法 对压力信号直接进行互相关算法,其峰值往往会在时间延迟为零处。造成这一现象的原因在于信号的稀疏性差。对信号采用加权残差算法能够有效地提高稀疏性,同时在不改变时间特征的前提下保留住信号的压降特征。加权残差算法的数学表达式为: (11) (12)式中:α为加权参数。从式(14)和(15)可以看出,如果原信号相对平稳,其加权残差信号将一直保持在零附近,当原信号有下降或上升时,其加权残差信号也会偏离零值下降或上升。因此,加权残差算法可以提高信号的稀疏性,对后续进行互相关算法提供帮助。 2.3 SVD-NMF定位方法步骤 通过对管道泄漏信号进行奇异值分解的结果,确定有效奇异值的个数初始化NMF的矩阵W和H,实现管道泄漏的检测与定位,其定位方法流程如图5所示,主要步骤如下: ①分别对首尾站点的两泄漏信号x(k),y(k)进行滑动窗口截取,得到二维Hankel矩阵X∈Rm×n,Y∈Rm×n;②进行奇异值分解,计算奇异值差分谱,确定有效奇异值个数k;③截取奇异值分解矩阵U前k行对矩阵W进行初始化,矩阵V前k列对矩阵H进行初始化,并根据式(3)、式(4)的迭代规则进行迭代,当矩阵W和H的变化小于阈值时,停止迭代,并相乘计算新矩阵X,重构去噪后的新信号x′(k),y(k);④将NMF算法去噪后的信号进行加权残差计算,得到Δx(k),Δy(k),并判断最小值的绝对值是否超过阈值,如超过则判定泄漏发生;⑤对两残差信号进行互相关计算,得到时延数,最后根据式(9)进行定位,检测软件发出报警并显示泄漏点位置。 为了验证SVD-NMF算法计算两信号时延的准确性,对实验室搭建的管道泄漏实验平台进行检测。管道总长为113 m,两传感器间距为93 m,在3个不同位置安装阀门来模拟泄漏,以进水端压力变送器的位置为原点,泄漏点1、2、3的位置分别为5.4 m、21.4 m和69.4 m,通过计算得到波速为1 120 m/s。整个实验系统示意图如图6所示。 图6 泄漏检测系统示意图 当1号泄漏点发生泄漏时,采集两端压力变送器的电信号其波形如图7所示,其中采样率为500 Hz。对两信号直接进行加权残差和互相关计算得到的互相关谱如图8所示,可以看出由于信噪比较低,互相关谱的峰值位置在零点处,无法得到准确的时延数。 对两原始信号进行SVD-NMF降噪处理,得到降噪后的信号如图9所示。后对两信号进行加权残差计算和互相关计算,得到的互相关谱如图10所示。对比图8和图10的互相关谱,SVD-NMF降噪有效地提高了信噪比,得到的时延数也更加精确。提取互相关谱峰值,得到时延为74 ms,结合波速、和管道长度信息得出泄漏位置为5.06 m,与泄漏点1位置5.4 m非常接近。 图8 含噪互相关谱 图9 SVD-NMF算法处理后信号 图10 SVD-NMF算法处理后互相关谱 在1号~3号泄漏点分别进行五次泄漏实验,定位结果如表1所示。所示结果表明,采用SVD-NMF算法对原信号进行降噪处理,对于不同位置的泄漏点都能进行较为准确的定位,平均定位误差为0.80 m。 表1 信号去噪前后互相关得到的时延数 单位:m 同时,为了对比SVD-NMF算法与其他算法的降噪效果,采用8级db02小波对相同信号降噪后进行定位,并与SVD-NMF定位结果进行对比,其结果在表2列出。通过结果对比,可以看出,在信噪比较低的情况下,采用小波降噪互相关峰值位置在零附近,因此无法进行准确的定位。而SVD-NMF算法能够对压力信号进行降噪并得到更高的定位精度。 表2 SVD-NMF与小波降噪算法的时延数对比 单位:m 对新疆某管线的压力数据进行处理,查询工作日志,在距出站0.66 km处发生泄漏。管线长23.62 km,压力波传播速度为1170 m/s,采样率为20 Hz。对泄漏时刻管道两端站点的压力信号提取并处理,其波形如图11所示。观察波形可以发现存在明显的压力下降。对两信号直接进行加权残差计算和互相关计算的结果如图12所示。 图11 含噪原始信号 图12 含噪互相关谱 对两信号进行SVD-NMF降噪处理,得到降噪后的信号如图13所示。再进行加权残差计算和互相关计算,得到的互相关谱如图14所示。可以看出,由于原信号的信噪比较高,两互相关谱波形差别并不大。但取互相关峰值位置分别为356和367,根据式(9)计算出采用NMF算法前后泄漏定位分别为1.40 km和1.08 km。对比工作日志的泄漏位置,在采用SVD-NMF算法后,泄漏定位的精度有所提升。 图13 NMF算法处理后信号 图14 NMF算法处理后互相关谱 对多条管线的工作日志显示的发生泄漏时的信号进行SVD-NMF算法进行定位,其定位误差与未去噪定位误差的对比结果如表3所示。由表3可以看出,采用SVD-NMF算法后,管道泄漏的定位误差有所下降。 表3 去噪前后定位误差比较 单位:km 在管道泄漏检测中,由于周边环境复杂,采集的压力信号易受到多种噪声干扰,导致定位精度降低。针对这一问题,本文提出基于SVD-NMF的泄漏信号增强算法,该算法通过将奇异值分解与非负矩阵分解相结合,提高了算法的稳定性和运算速度。通过对压力信号进行SVD-NMF处理,去除了噪声干扰,提高定位精度。实验证明,该方法能够有效地对压力信号进行去噪,计算得到的泄漏定位精度更高。 [1] Wang L,Wang J,Gao X,et al. Summary of Detection and Location for Oil and Gas Pipeline Leak[C]//Control and Decision Conference(CCDC),2013 25th Chinese. IEEE,2013:821-826. [2] 韩玲娟,王强,杨其华,等. 基于分布式光纤传感的水下输气管道泄漏检测与定位分析[J]. 传感技术学报,2015,28(7):1097-1102. [3] Zhang Y,Chen S,Li J,et al. Leak Detection Monitoring System of Long Distance Oil Pipeline Based on Dynamic Pressure Transmitter[J]. Measurement,2014,49(1):382-389. [4] Ge C,Wang G,Ye H. Analysis of the Smallest Detectable Leakage Flow Rate of Negative Pressure Wave-Based Leak Detection Systems for Liquid Pipelines[J]. Computers and Chemical Engineering,2008,32(8):1669-1680. [5] 郭晨城,文玉梅,李平,等. 采用EMD的管道泄漏声信号增强[J]. 仪器仪表学报,2015,36(6):1397-1405. [6] 路炜,文玉梅. 供水管道泄漏定位中基于互谱的时延估计[J]. 仪器仪表学报,2007,28(3):504-509. [7] 文玉梅,谢仁峰,杨进,等. 管道泄漏检测中的噪声自适应抑制[J]. 仪器仪表学报,2012,33(10):2228-2233. [8] 赵利强,王建林,于涛. 基于改进EMD的输油管道泄漏信号特征提取方法研究[J]. 仪器仪表学报,2013,34(12):2696-2702. [9] 文玉梅,由原,杨进,等. 固定干扰源存在下的管道泄漏检测和准确定位[J]. 声学学报,2013,38(1):80-84. [10] Sun J,Xiao Q,Wen J,et al. Natural Gas Pipeline Small Leakage Feature Extraction and Recognition Based on LMD Envelope Spectrum Entropy and SVM[J]. Measurement,2014,55(9):434-443. [11] Ostapkowicz P. Leakage Detection from Liquid Transmission Pipelines Using Improved Pressure Wave Technique[J]. Eksploatacja I Niezawodno,2014,16(1):9-16. [12] Mostafapour A,Davoodi S. Continuous Leakage Location in Noisy Environment Using Modal and Wavelet Analysis with One AE Sensor[J]. Ultrasonics,2015,62:305-311. [13] Yu X,Liang W,Zhang L,et al. Dual-Tree Complex Wavelet Transform and SVD Based Acoustic Noise Reduction and Its Application in Leak Detection for Natural Gas Pipeline[J]. Mechanical Systems and Signal Processing,2015,72/73:266-285. [14] Lee D D,Seung H S. Learning the Parts of Objects by Non-Negative Matrix Factorization[J]. Nature,1999,401(6755):788-791. [15] Shon S,Mun S,Han D,et al. Non-Negative Matrix Factorization-Based Subband Decomposition for Acoustic Source Localization[J]. Electronics Letters,2015,51(22):1723-1724. [16] Ozerov A,Févotte C. Multichannel Nonnegative Matrix Factorization in Convolutive Mixtures for Audio Source Separation[J]. IEEE Transactions on Audio Speech and Language Processing,2010,18(3):550-563. [17] 刘中健,赵知劲,尚俊娜. 快速NMF盲源分离算法[J]. 信号处理,2014,30(6):699-705. [18] 胡永刚,张雄伟,邹霞,等. 改进的非负矩阵分解语音增强算法[J]. 信号处理,2015,31(9):1117-1123. [19] 王帆,杨雅伟,谭帅,等. 基于稀疏性非负矩阵分解的故障监测方法[J]. 化工学报,2015,66(5):1798-1805. [20] 任建新,边琦,张鹏,等. 一种基于SVD和改进自适应算法的科氏流量计气体信号频率解算方法[J]. 传感技术学报,2013,26(10):1405-1408. [21] 查翔,倪世宏,张鹏. 一类非线性信号去噪的奇异值分解有效迭代方法[J]. 电子与信息学报,2015,37(6):1330-1335. [22] Zhao X,Ye B. Selection of Effective Singular Values Using Difference Spectrum and Its Application to Fault Diagnosis of Headstock[J]. Mechanical Systems and Signal Processing,2011,25(5):1617-1631. [23] Hoyer P O. Non-Negative Matrix Factorization with Sparseness Constraints[J]. Journal of Machine Learning Research,2004,5(Nov):1457-1469. SVD-NMF Based Denoising Algorithm for Pipeline Leak Signal XIAONan,LIJian*,XIAOQiyang (State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China) In the pipeline leak detection,noise in pressure signals decrease the location accuracy of traditional cross-correlation method. The traditional denoising algorithm cannot adapt to environment,and the effect is not good. Therefore,a denoising algorithm for pipeline leakage signal based on nonnegative matrix factorization(NMF)combined with singular value decomposition(SVD)is proposed. The leak signals are decomposed by singular value decomposition to determine the NMF’s order and initialize the matrix. The improved NMF algorithm is adopted to factorize the original signals and denoised signals are obtained. The time delay is calculated by cross-correlation method,and the leak location is accomplished with the combination of the stress wave velocity. Experimental results show that the SVD-NMF algorithm can reduce the number of iterations and enhance the speed of denoising significantly. In the application of leak detection,the algorithm can remove noise and improve the location accuracy. pipeline leak location;NMF;SVD;cross-correlation;negative pressure wave 肖 楠(1992-),男,天津大学精密仪器与光电子工程学院硕士研究生,研究领域:振动信号检测和处理方法,xi-aonan430@tju.edu.cn;李 健(1973-),男,天津大学精密仪器与光电子工程学院教授,研究领域:管道安全检测、无损检测,tjupipe@tju.edu.cn; 肖启阳(1989-),男,天津大学精密仪器与光电子工程学院博士研究生,研究领域:振动信号处理,机械故障诊断与识别,yisuoyanyu058@126.com。 2016-06-23 修改日期:2016-09-07 TN911.72 A 1004-1699(2017)01-0101-08 C:7220 10.3969/j.issn.1004-1699.2017.01.019


2 基于SVD-NMF和互相关法的泄漏定位

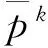
3 SVD-NMF算法实验验证


4 实际数据采集与处理




5 结语

