列车纵向车钩力不确定性研究

郑雪,薛齐文

(大连交通大学 土木与安全工程学院，辽宁 大连 116028)*



列车纵向车钩力不确定性研究

郑雪,薛齐文

(大连交通大学 土木与安全工程学院，辽宁 大连 116028)*

基于区间摄动理论，引入多参数数学简化方法构建列车制动系统模型，在已有车钩力模型的基础上，建立了列车纵向动力学的不确定性区间分析模型.针对多参数的制动系统模型，分别考虑制动控制阀特性、制动缸充气特性、制动波传播速度特性等参数的不确定性，利用所建不确定性区间分析模型，探讨纵向车钩力的区间变化范围，并给出了相关的数值算例.结果表明制动系统中相关参数变化会对最大车钩力造成不同程度的影响.其中，制动控制阀特性参数对尾车最大压钩力影响最大，制动波传播速度特性参数对其影响最小.制动缸充气速度和制动波传播速度会随着制动时间的延长而减慢，这一改变均会使最大车钩力较初始的最大车钩力变大.

多参数;纵向动力学;区间摄动理论;不确定性

0 引言

随着世界经济的迅猛发展，铁路运输日益受到人们的重视.由于列车纵向动力学性能的好坏会直接影响列车运行的安全性，所以当列车制动时所产生的纵向力超过了列车所能承受的极限, 就会导致一系列安全事故的发生，众多学者对此开展了很多研究[1- 3].

针对列车纵向动力学的研究，制动系统特性的研究是其核心问题之一.目前国内外对于制动系统特性的计算方法主要有三种：多段线性拟合法、基于气体流动方程的计算方法、单参数数学计算方法.这三种方法计算得出的制动缸充气特性都与实际情况相差很大[4].本文引入多参数数学简化方法来探讨列车制动系统相关参数变化对最大车钩力的影响，从而为后续的计算提供有效的制动特性数据.

在以往的纵向动力学分析中，学者们通常将系统参数及初始条件等均视为确定量进行分析求解，但列车的纵向动力学研究是一个高度复杂的不确定过程，这就使分析得出的相关数据存在一定的误差甚至是错误.为了得到更加准确且对工程实际有指导意义的分析结果，通过考虑制动系统相关参数的不确定性，建立列车纵向动力学不确定性区间分析模型来研究其纵向动力学不确定性问题.

对于不确定性问题，目前主要存在三种方法进行求解: 随机模型、模糊模型、区间分析模型.由于区间分析模型无需依赖大量统计数据来描述不确定参数的概率分布或者隶属函数，仅通过不确定参数的取值范围，便能求解出响应的区间范围，更加符合工程实际[5- 8].目前区间分析模型在其他领域应用较广，并且已取得了很多成果，但是对于列车纵向动力学的应用而言还相对较少.

鉴于以上考虑，本文基于区间摄动理论，引入多参数数学简化方法构建列车制动系统模型，在已有车钩力模型的基础上，建立了列车纵向动力学的不确定性区间分析模型.分别考虑了制动系统中相关参数的不确定性，对模型进行最大车钩力数据分析.将不确定性计算结果与确定性结果对比表明，所提区间分析模型在对列车纵向动力学不确定性问题进行分析时是可行的.

1 纵向动力学区间模型

根据牛顿第二定律F=ma，列车运行过程中针对某一节车厢仅考虑制动力与车钩力作用，则P-FC=ma,其中P为制动力，FC为车钩力.在纵向动力学研究范围中，列车中每节车厢可以抽象成一个质量弹簧阻尼系统，所以FC=Cv+Kx,由此可以得到列车动力学方程Ma+Cv+Kx=P.列车纵向动力学模型如图1所示.

图1 研究对象

对于确定性的列车动力学问题，由给定的初始条件，可以得到如下方程：

其中:向量φ由列车中车辆编组总数N、制动控制阀特性参数λ、制动波传播速度特性参数γ、制动缸充气特性参数κ等参量组成，可以利用确定性的数值方法进行求解.

式中:M(φc)、C(φc)、Kφc)、P(φc)、a(φc)、v(φc)和x(φc)是与中值对应的质量矩阵阻尼矩阵、刚度矩阵、等效载荷矩阵、位移二阶导数向量、位移一阶导数向量和位移向量；ΔM、ΔC、ΔK、Δa、Δv、Δx则分别为相对应的区间不确定性矩阵.

列式(2)在任意时刻均成立，忽略展开过程中的高阶小项，可得到下面方程组：

其中:ΔP1=ΔP-(ΔM·a(φc)+ΔC·v(φc)+ΔK·x(φc))，由此可知，不确定方程式(2)可以分离为确定性部分和不确定性部分，各式中均含有与时间相关的项.

采用时域精细算法进行时域离散[11- 12]，在每一个离散时间段内，位移及梯度变换公式可分别写为：

由此可得：

在第一个时间段内，x0由给定的初始条件求得，在其他的第N个时间段内，x0可以由上一个时间段按下式求得：

由上述两个确定性的递推列式(7)～式(8)，以及给定的区间参数和初始条件，可以依次求得每个时间段内的x0，x1，x2，…，xm和Δx0，Δx1，Δx2，…，Δxm，从而求得各时间段末的位移和速度.在任意时刻，节点位移场与速度场的上、下界分别为：

2 制动系统模型

影响任意两节车厢间车钩力大小的主要因素就是这两节车厢所受的制动力.首先要用数学方法得到制动缸充气压强，因此引用多参数数学简化方法，通过以下公式描述制动缸在紧急制动工况下的充气特性[3]：

式中：Ps(ts)为紧急二段阀作用时制动缸多线段性充气压力；ts为紧急二段阀作用结束时间；tm为制动缸压力上升到最大值时的时间；td,i为第i辆车制动缸开始充气时所用的时间；tΔ,i为第i辆车与第1辆车制动缸充气时间的差值；λ为制动控制阀特性参数；Pmax为制动缸压力上升达到的最大值.其中，

式中：γ为制动波传播速度特性参数；κ为制动缸充气特性参数；N为列车中车辆的编组总数；t1为第1辆车的制动缸开始充气时所用的时间；tN为第N辆车的制动缸开始充气时所用的时间；T1为第1辆车的制动缸充气所用的时间；TN为第N辆车的制动缸充气所用的时间.

对于货运列车的基础制动系统基本都采用闸瓦制动，那么在进行车辆制动力计算时，首先需要将制动缸压力转化为闸瓦压力，因此机车车辆中每块闸瓦的闸瓦压力可表示为：

其中：dz为制动缸直径；ηz为基础制动装置计算传动效率；nz为制动缸数量；γz为制动缸倍率；nk为闸瓦数量；pi为制动缸内空气压强.

根据车轮与闸瓦间的作用力关系，车辆在制动过程中的制动力为：

其中：φK为车轮与闸瓦间的摩擦系数;K为闸瓦压力.

由此可见，车轮与闸瓦间的摩擦系数直接影响了制动力的大小，因此根据《列车牵引计算规程》，通过列车制动初速度和瞬时速度可以得到不同材质闸瓦的摩擦系数，进而可以求出任意时刻每节车厢所受到的制动力.

根据上述公式构建列车制动系统模型，结合已有车钩力模型，根据区间摄动理论建立纵向动力学区间分析模型，分别考虑制动参数的不确定性，即可得到任意两节车厢间的车钩力变化范围.

3 数值算例

以分析30辆车的纵向动力学问题为例，讨论制动系统相关参数的不确定性对最大车钩力的影响.采用一辆机车(HXD1)加29辆拖车(C80)的编组形式，总分析时域为30 s，时间段长取为0.02 s，制动缸压力最大值为430 kPa.初速度为100 km/h,列车车钩间隙一致为10 mm，缓冲器为HM-1型，其中λ、γ和κ初始值均取1.

计算结果如下所示，其中表1列出了紧急制动和常用制动两种工况下，首车、中车和尾车位置所受到的最大车钩力及其发生时刻，表1～3给出了紧急制动工况下，制动控制阀特性参数λ、制动缸充气特性参数κ和制动波传播速度特性参数γ分别变化0.5%时对首车、中车和尾车的最大车钩力影响，表4～6给出了紧急制动工况下，任意两个参数组合变化0.5%时，对尾车最大车钩力的影响.

表1 不同制动工况下不同位置的最大车钩力以及发生时刻

表2 当λ变化0.5%时，最大车钩力响应区间 kN

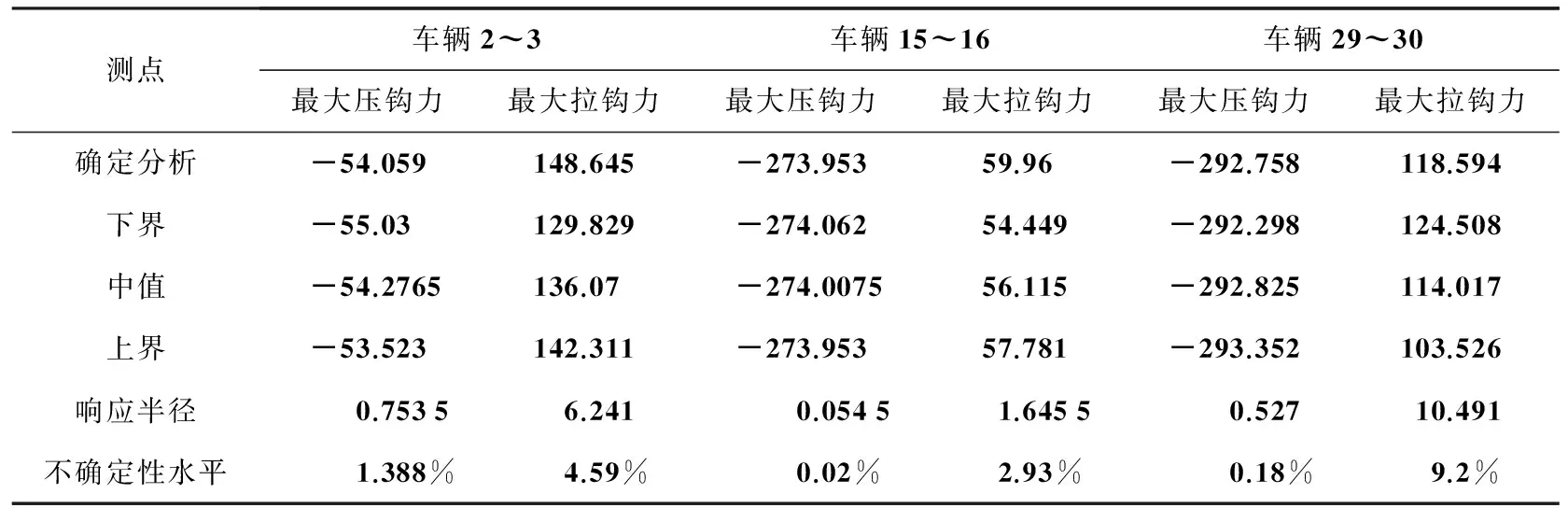
表3 当κ变化0.5%时，最大车钩力响应区间 kN

表4 当γ变化0.5%时，最大车钩力响应区间 kN

表5 当λ和κ组合变化0.5%时，第29与30辆车之间最大车钩力响应区间

表6 当λ和γ组合变化0.5%时，第29与30辆车之间最大车钩力响应区间

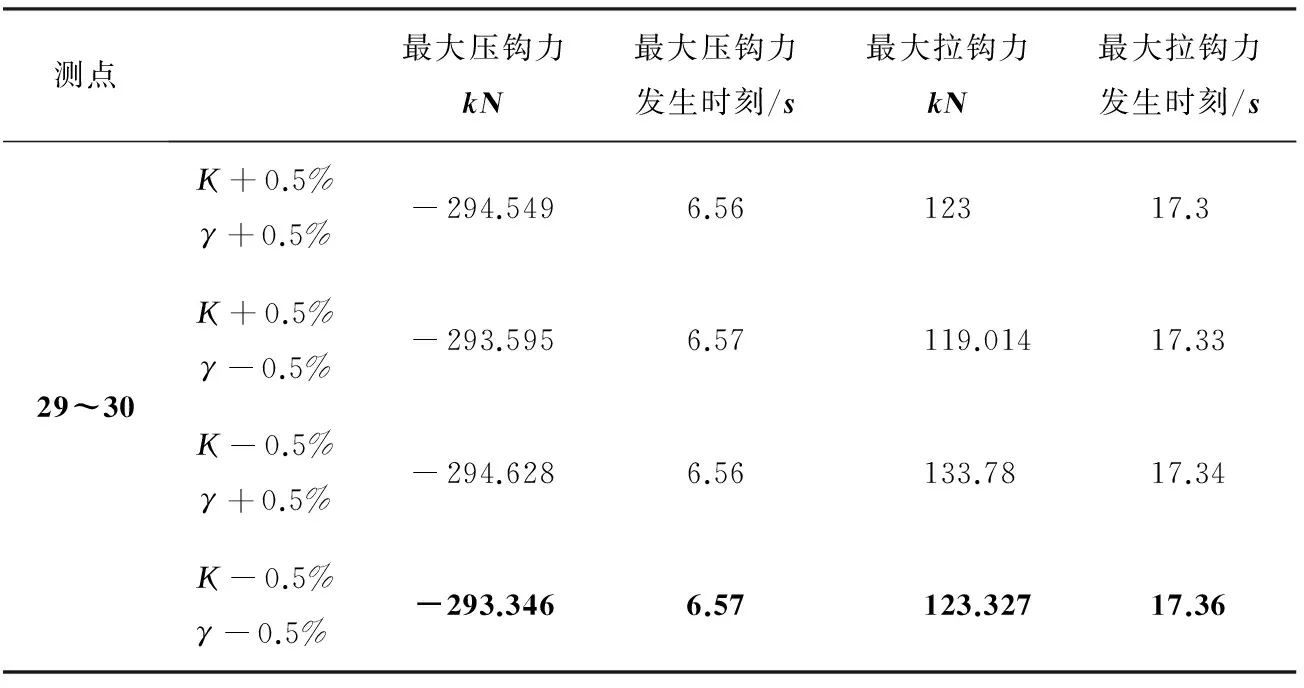
表7 当κ和γ组合变化0.5%时，第29与30辆车之间最大车钩力响应区间

计算结果表明：

(1)从计算结果可以看出，基于区间摄动理论，引入多参数数学简化方法构建制动系统模型，结合车钩力模型建立的纵向动力学区间模型可以求解列车最大车钩力的不确定性问题;

(2)从表1中数据可以得知，常用制动工况下最大车钩力发生在列车中部,由于最大拉钩力数值很小，可以忽略不计，在此不进行讨论.在紧急制动工况下，由于制动时间短，制动缸压强在短时间内迅速增大，以达到快速制动的目的，但势必造成车厢间的纵向冲动，所以无论压钩力还是拉钩力，都比常用制动时的车钩力大很多.其中，最大拉钩力发生在列车头部，最大压钩力发生在列车尾部;

(3)从表2～表4可以看出，在紧急制动工况下，λ变化对最大车钩力影响最大，К变化对其影响最小.其中，λ变化0.5%时，对首车及尾车最大压钩力影响较大，不确定性水平分别为6.91%和5.26%；К变化0.5%时，对首车及尾车最大拉钩力影响较大，不确定性水平分别为4.59%和9.2%；γ变化0.5%时，对首车及尾车最大压钩力影响较大，但与λ相比，不确定性较小，分别为3.88%和1.72%;

(4)从表5可以看出，当λ与К同时变化时，在λ增大0.5%且К变化0.5%时，第29与第30节车厢之间的最大压钩力减小，分别减小了0.29%和0.24%;

(5)从表6可以看出，当λ和γ同时变化时，只有在λ减小0.5%且γ减小0.5%这种情况下，最大压钩力减小了0.04%;

(6)从表7可以看出，当К和γ同时变化时，四种组合变化均使最大车钩力有不同程度的增大.

由于在紧急制动工况下，发生在尾车位置的最大压钩力比发生在首车位置的最大压钩力数值要大得多，所以，在研究列车纵向动力学过程中，重点是对尾车位置的最大压钩力进行分析.图2～图5分别描述了紧急制动工况下，单参数变化0.5%以及任意两个参数组合变化0.5%时对尾车最大压钩力的影响.通过对比，可以得到以下结果：

(1)从图2中可以看出，当λ增大0.5%时，最大压钩力最小；反之，最大压钩力最大.当К减小0.5%时，最大压钩力减小，当К增大0.5%，γ增大或者减小0.5%时，最大压钩力均增大;

(2)从图3中可以看出，当λ增大时，不管К增大或者减小，最大压钩力均减小;

(3)从图4～图5中可以看出，К和γ同时变化对最大压钩力的影响比λ和γ同时变化对其影响要大.

图2 单参数变化时，第29～30辆车之间车钩力

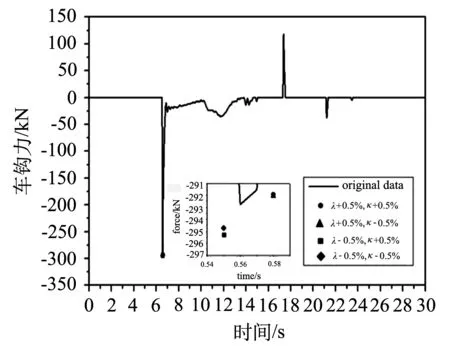
图3 λ与К同时变化时，第29～30辆车之间车钩力

图4 λ与γ同时变化时，第29～30辆车之间车钩力

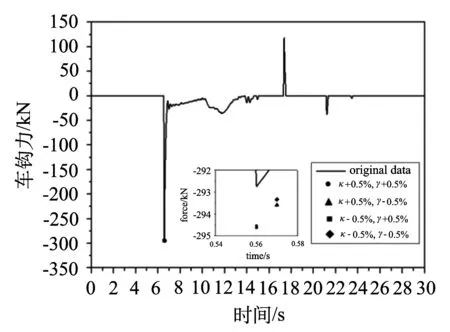
图5 γ与К同时变化时，第29～30辆车之间车钩力

4 结论

基于区间摄动理论，引入多参数数学简化方法构建制动系统模型，结合车钩力模型建立了列车纵向动力学区间模型.针对该模型对30辆车紧急制动工况下的最大车钩力不确定性区间响应进行了分析，主要考虑了制动控制阀特性参数、制动波传播速度特性参数和制动缸充气特性参数的变化对于最大车钩力的影响，根据数值算例的结果，可以得到如下结论：

(1)基于区间摄动理论，引入多参数数学简化方法构建制动系统模型，结合车钩力模型建立的纵向动力学区间模型对紧急制动工况下的列车最大车钩力不确定性问题研究是有效的;

(2)当制动控制阀特性参数、制动波传播速度特性参数和制动缸充气特性参数发生同等程度的变化时，对应的车钩力变化程度是不同的.λ变化对最大车钩力影响最大，К变化对其影响最小.γ代表制动波的传播速度特性，由于参数最初取值为1，表明制动波匀速传播，因此当制动波传播速度特性参数发生变化时，表明制动波非匀速传播，必然会导致最大压钩力的增大.所以当制动波传播速度特性参数与其他参数组合变化时车钩力均有不同程度的增大.

由于制动波的传播速度和制动缸充气速度会随着制动时间的延长而减慢，对于这一过程如何使数学方法进行描述还有待更进一步深入研究.

[1]钱立新．世界重载铁路运输技术的最新进展[J]．机车电传动,2010(1):3- 7.

[2]李芾，安琪，黄春蓉．中国铁路机车车辆装备技术发展及展望[J].中国铁路,2012(11):11- 17.

[3]魏伟，杜念博．重载列车制动管路对制动性能的影响[J]．交通运输工程学报,2011，11(5):49- 54.

[4]孙树磊. 重载列车纵向冲动动力学研究[D].成都：西南交通大学，2014.

[5]IMPOLLONIAN,MUSCOLINOG.Intervalanalysisofstructureswithuncertain-but-boundedaxialstiffness[J].ComputerMethodsinAppliedMechanicsandEngineering, 2011,200(21/22):1945- 1962.

[6]杜秀云，唐祯安，薛齐文.瞬态热传导温度场不确定性区间数值分析[J].功能材料,2013，44(11):1558- 1561.

[7]陈塑寰,裴春艳.不确定二阶振动控制系统动力响应的区间方法[J].吉林大学学报,2008,38(1):94- 98.

[8]丁健峻,薛齐文,刘旭东.基于区间摄动理论的隧道结构响应分析[J].大连交通大学学报,2015,36(1):68- 71.

[9]邱志平,马利红,王晓军.不确定非线性结构动力响应的区间分析方法[J].力学学报,2006,38(5):645- 651.

[10]张翼，薛齐文.TSV封装孔形态参数对焊点热疲劳寿命的影响[J].半导体技术,2015,40(9):684- 691.

[11]YANGHAITIAN.Aprecisealgorithminthetimedomaintosolvetheproblemofheattransfer[J].NumericalHeatTransfer,PartB,1999,35(2):243- 249.

[12]郭红玲，杨海天,赵潇.蚁群算法求解弹性本构参数区间反问题[J]．工程力学,2012,29(1):7- 12.

Uncertainty Study of Train Longitudinal Coupler Force

ZHENG Xue,XUE Qiwen

(School of Civil and Safety Engineering,Dalian Jiaotong University,Dalian 116028,China)

A train braking system was built by multi-parameter mathematic simplified method, and the train longitudinal dynamics uncertain interval model is presented by interval perturbation theory based on the used model of coupler force. This thesis respectively analyzes the brake control valve characteristic, brake cylinder inflation characteristic and brake wave propagation characteristic parameter uncertainty of train air brake system for multi-parameter mathematic simplified method, and the uncertain interval model is used to discuss the variation range of couple force and provide a relevant numerical example. The results show that relevant parameters in the brake system will affect maximum coupler force in varying degrees. The brake control valve characteristic parameter has the most important influence on tail-car maximum compress coupler force, and brake wave propagation characteristic parameter has minimum impact. The brake cylinder inflation characteristic and brake wave propagation characteristic parameter will be slower by prolonging braking time, and the whole process will make coupler force increasing.

multi-parameter; longitudinal dynamics; interval perturbation theory; uncertainty

1673- 9590(2017)01- 0038- 07

2016- 01- 03

国家自然科学基金资助项目(10802015);辽宁省自然科学基金联合基金资助项目(2015020119)

郑雪(1990-)，女，硕士研究生;薛齐文(1976-)，男，教授，博士，主要从事车辆动力学方面的研究

E-mail:983248165@qq.com.

A