关于画法几何学中直线的迹点求解方法分析

刘剑锋



关于画法几何学中直线的迹点求解方法分析

刘剑锋

（湖南科技学院 电子与信息工程学院，湖南 永州 425199）

文章对空间直线任意位置的迹点求解方法进行了分析和归纳，重点是从几何学的角度对利用定比性求解侧平线的迹点加以证明，为后续学习人员直接引用定比性求解直线迹点提供理论依据。

迹点；侧平线；定比性；求解

1　引　言

迹点是指直线和投影面的交点。直线和水平投影面的交点称为水平迹点，和正面投影的交点称为正面迹点，和侧面投影的交点称为侧面迹点，分别用M、N、S表示。在《画法几何及机械制图》、《画法几何学》、《机械制图》等众多机械专业教材中对于迹点这一内容描述的篇幅较少，其中并未对迹点的求解过程加以详细讲解[1-3]。但是在相关习题集中关于迹点的题型相对较多较全，导致学生在做题过程中存在诸多疑惑[4-5]。经查阅相关文献，很少有关于迹点的详细求解过程，尤其是利用定比性求解[6-7]。因此，将迹点的求解过程明朗化, 对帮助学生理解和增加学习积极性具有现实意义。

2　各类空间直线迹点求解方法探讨

画法几何中，按照空间直线对基本投影体系的相对位置关系，可将直线分为三大类：一般位置直线、投影面平行线和投影面垂直线，后两类又称为特殊位置直线，根据投影面的不同，特殊位置直线又可分为水平线（∥水平面）、正平线（∥正平面）、侧平线（∥侧平面）和铅垂线（⊥水平面）、正垂线（⊥正平面）、侧垂线（⊥侧平面）。

2.1一般位置直线的迹点

一般位置直线的迹点求解常用的方法是根据点的两面投影确定迹点位置，求解过程相对简单。

图1为一般位置直线的H/V两面投影，它的迹点详细求解过程如下：

（1）如图2所示，分别延长空间线段AB在水平投影面的投影ab与投影轴OX相交于点n，延长空间线段AB在正立投影面的投影a¢b¢与投影轴OX相交于点m¢;

（2）根据点的投影特性可知，点的两面投影的连线垂直于投影轴，如图3所示，分别过点n、m¢作垂直于OX的垂线；

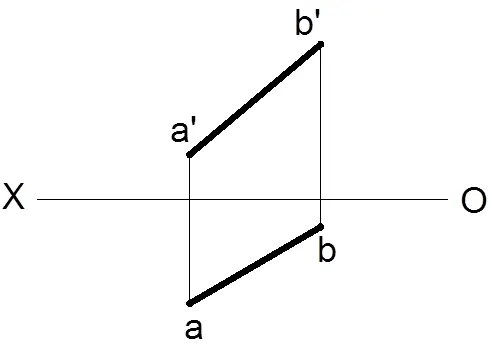
图1.一般位置直线

图2.步骤一

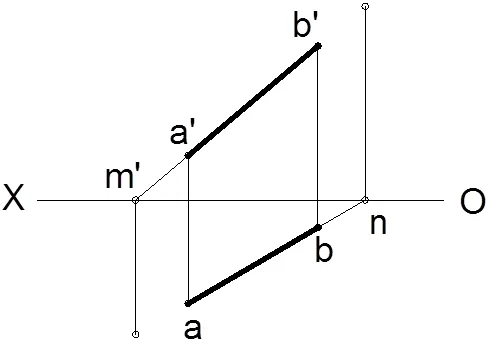
图3.步骤二

图4.步骤三

（3）在水平投影面延长ab与投影轴连线相交于点M，在正立投影面延长a¢b¢与投影轴连线相交于点N。其中迹点M在水平面的投影m与之重叠，因此m带括号，迹点N在正立面的投影n¢与之重叠，因此n¢带括号，如图4所示。

2.2投影面平行线的迹点

投影面平行线分为水平线、正平线、侧平线三种，求解过程如下：

（1）水平线。根据水平线的定义可知，水平线平行于水平投影面，与其他两个投影面倾斜，它的迹点分别在正立投影面和侧立投影面上，迹点标记是N点和S点。图5是水平线在H/V两面投影体系中的投影，若采用点的投影规律求解迹点，则需要引入三面投影体系才能求解，如图7所示。

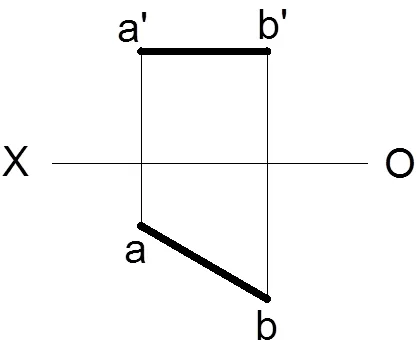
图5.水平线

图6.正平线

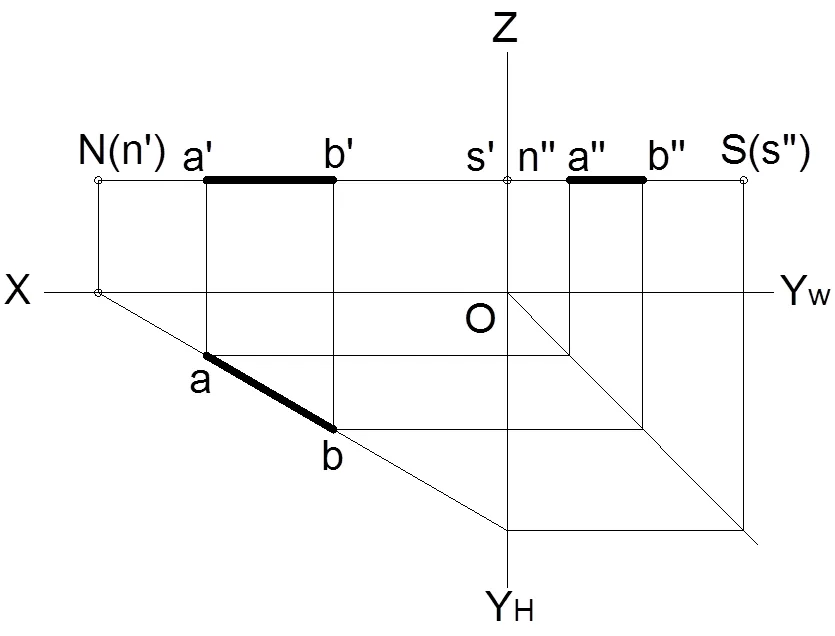
图7.水平线的迹点

（2）正平线。根据正平线的定义可知，正平线平行于正立投影面，与其他两个投影面倾斜，它的迹点分别在水平投影面和侧立投影面上，迹点标记是M点和S点。图6是正平线在H/V两面投影体系中的投影，若采用点的投影规律求解迹点，则同样需要引入三面投影体系才能求解，如图8所示。

图8.正平线的迹点

（3）侧平线。根据侧平线的定义可知，侧平线平行于侧立投影面，与其他两个投影面倾斜，它的迹点分别在水平投影面和正立投影面，迹点标记是M点和N点。若采用点的投影规律求解迹点，则需要引入三面投影体系才能求解。

由上述可知，投影面平行线的两个迹点需要在三面投影体系中才能求解。那么能否在不引入三面投影体系的前提下求解？可以利用直线上点的定比性求解。

定比性指的是直线上点的投影必须在该直线的同面投影上，且点分线段长度之比等于其投影长度之比。定比性常用于解决直线上点的投影问题。

以侧平线为例，已知侧平线AB的两面投影分别为ab和a¢b¢，利用定比性求解它的正面迹点M和水平迹点N。

图9所示为侧平线AB在三投影面体系中的状态，它与水平投影和正面投影的迹点分别为M和N点，图10所示为侧平线迹点的H/V两面投影，图11所示为利用定比性求解两迹点，图12所示为沿X方向从右往左看侧平线AB，做辅助线得交点E。

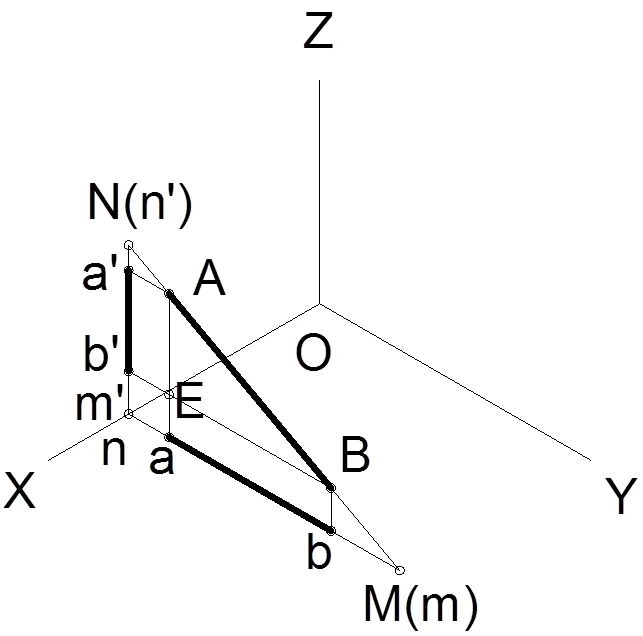
图9.侧平线的三面投影体系

图10.侧平线的迹点

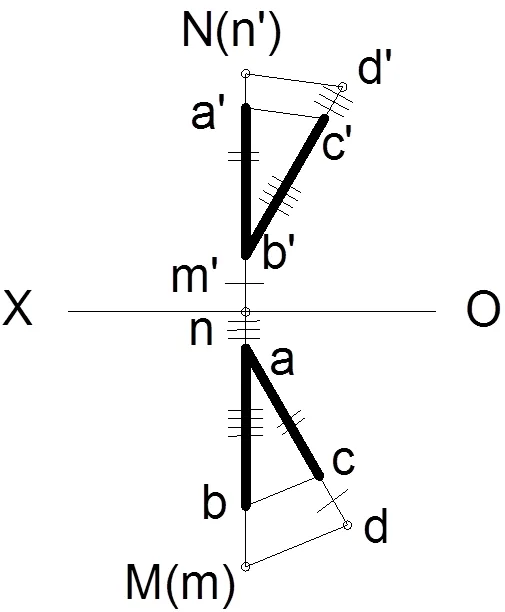
图11.定比性图解侧平线迹点

图12.侧平线的侧视图

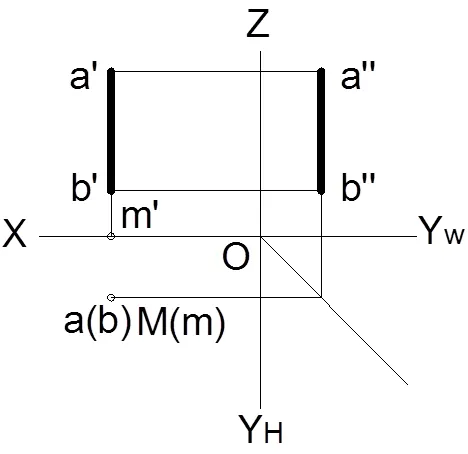
图13.铅垂线的迹点

①在图9中，以点B在直线AM上理解，根据直线上点的定比性，可得到图11，并存在以下关系：

ac=a¢b¢, cd=b¢m¢

ab:bm=ac:cd=a¢b¢:b¢m¢

在图9中，以点A在直线NB上理解，根据直线上点的定比性，可得到图11，并存在以下关系：

ab=b¢c¢, na=c¢d¢

a¢b¢:n¢a¢=c¢b¢:d¢c¢=ab: na

②结合图9和12从几何的角度可证明如下关系：

∵△BEA∽△MbB

∴EB:bm=AE:Bb

又∵EB=ab, AE=a¢b¢,Bb=b¢m¢

∴ab:bm=a¢b¢:b¢m¢

同理△BEA∽△Aa¢N

可得EB:a¢A=AE:Na¢=ab:na=a¢b¢:n¢a¢

因此，侧平线的迹点存在图10中的定比关系，同样水平线和正平线也能用定比性进行求解。

2.3投影面垂直线的迹点

投影面垂直线分为铅垂线、正垂线、侧垂线三种，求解投影面垂直线迹点的方法需要引入到三面投影体系，根据点的投影特性进行求解。如图13-15所示，分别是铅垂线的迹点、正垂线的迹点、侧垂线的迹点，由图可知该类型直线的迹点有且仅有一个。

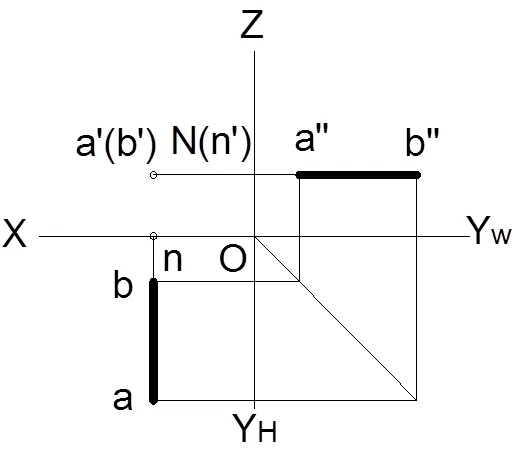
图14.正垂线的迹点

图15.侧垂线的迹点

3　结束语

文章对任意位置空间直线的迹点的求解均加以作图解释，得出以下结论：

（1）一般位置直线和投影面平行线存在2个迹点，投影面垂直线有且仅有1个迹点；（2）一般位置直线的迹点可以在两面投影直接图解得到，而投影面平行线和投影面垂直线的迹点需引入三面投影体系，根据点的投影特性才能求解；（3）从几何学的角度对利用定比性求解侧平线迹点的原理加以证明，为后续人员的直接引用提供理论依据。

[1]华中科技大学等院校编.画法几何及机械制图(第七版)[M].北京:高等教育出版社,2016.

[2]大连理工大学工程图学教研室编.画法几何学(第七版)[M].北京:高等教育出版社,2016.

[3]清华大学工程图学及计算机辅助设计教研室编,机械制图(第五版)[M].北京:高等教育出版社,2006.

[4]华中科技大学等院校编.画法几何及机械制图习题集(第七版)[M].北京:高等教育出版社,2016.

[5]大连理工大学工程图学教研室编.画法几何习题集(第五版)[M].北京:高等教育出版社,2016.

[6]繆宪文.关于直线几个图学问题的思考[J].安徽建筑工业学院学报(自然科学版),2005,(6):103-106.

[7]叶晓芹.关于侧平线几个图学问题的探讨[J].重庆建筑大学学报,1999,(4):102-105.

（责任编校：宫彦军）

2017－03－01

湖南科技学院教学改革研究项目（项目编号XKYJ2017053）。

刘剑锋（1985－），男，湖南永州人，湖南科技学院机械专任教师，工程师，研究方向为机械制图教学与机械结构轻量化设计等。

TH126.2

A

1673-2219（2017）10-0075-02