基于几何模型的惯性辅助PPP周跳修复与快速重新收敛

付粉娥

(内蒙古自治区地图院,内蒙古 呼和浩特 010051)

0 引 言

精密单点定位技术(PPP)可在全球范围内实施单机作业,具有成本低、灵活性好、精度高的优点,被广泛应用于空天地各种工程与科学领域中。随着多频多模GNSS的发展,PPP定位性能也得到了大幅度的提升。多频多模的GNSS为PPP定位增加了可见的卫星数,带来了更多的观测值,极大地改善了卫星几何构型,具有更好的定位精度和和收敛速度[1-2]。在海洋测绘、精细农业等开阔环境下,PPP技术能够取得与差分定位等同的效果。然而,GNSS本质上属于有源定位手段,在城市峡谷、高机动等复杂环境下,其信号具有脆弱性,将受到周围环境的遮挡干扰而出现周跳失锁现象,导致PPP模糊度重新初始化,影响定位精度及可靠性[3-5]。因此,许多学者提出周跳修复的方法来解决PPP重新初始化的问题。

周跳修复过程包括周跳探测、整数值估计以及相位观测值改正[6]。目前,周跳修复方法主要分为无几何模式和几何模式两大类,均采用超宽巷-宽巷-窄巷的组合方式进行逐级修复。Zhang提出利用L5-L3-Lx分级周跳修复的方法,首先利用LAMBDA和TRIM电离层模型得到电离层信息固定宽巷周跳,再利用LAMBDA方法固定由宽巷和无电离层组合导出的窄巷周跳,最后利用L5组合和L1、L2或GF组合任一观测来计算L1和L2的周跳,直到周跳被完全修复,该方法具有较好的鲁棒性[7]。Zhao借鉴三频模糊度固定的三频模糊度解算(TCAR)方法,形成超宽巷-宽巷-窄巷的周跳组合,逐步探测并修复[8]。Ye针对多系统PPP,提出了GPS+GLONASS双系统的周跳修复方法,由于系统间偏差比较稳定,经过历元间差分后可以消去,因此,多系统与单系统的周跳修复方法本质上是一样的[9]。在GNSS/SINS组合中,也有学者提出利用捷联惯导系统(SINS)递推的位置来辅助周跳探测和修复,但大部分集中于差分GNSS,且多数采用无几何模式的方法[10-12]。

本文采用非差非组合原始观测值建立周跳修复的历元间差分模型,通过PPP/SINS紧组合解算,标定惯性器件的系统误差,利用短时间内惯性递推的高精度位置约束历元间差分模型中的位置变化量,改善周跳解算方程的条件数,对解算得到的浮点周跳值进行整数固定,并再次用周跳探测检验周跳修复的正确性。即使周跳修复失败,PPP/SINS紧组合仍能加快重新收敛速度,进一步增强PPP定位在复杂环境下的性能。

联系人: 付粉娥E-mail: 15598048940@163.com

1 周跳修复的几何模型

周跳是指载波相位发生整周跳变的现象,周跳前后的相位观测值差一个整周数,将其作为参数,利用历元间差分模型进行解算,本文采用非差非组合的方式形成周跳修复方程。

原始伪距和相位观测方程为

(1)

式中: P为伪距观测值; φ为相位观测值; λ为载波波长; ρ为卫地距; dts为卫星钟差;dtr为接收机钟差;dtrp为对流层误差;dion为电离层误差;N为整周模糊度;εP和εφ分别是伪距和相位观测噪声。对式(1)原始观测值进行历元间差分,得到:

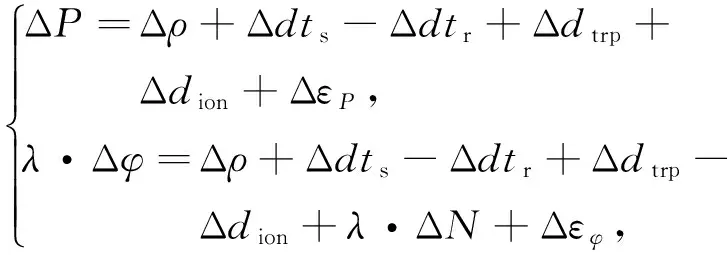
(2)

式中: Δ为历元间差分算子,当存在周跳时,ΔN不为零,需要作为待估参数进行求解； Δdts可以由精密星历提供； Δdtrp为对流层的变化量,在极短的时间内对流层十分稳定,该项可以忽略; Δdion为电离层变化量,通过电离层建模预报得到[3,7,9]； Δρ中包含卫星位置和接收机位置,具体表达式为

Δρ=ρ2-ρ1=e2(xs2-xr2)-e1(xs1-xr1)

=(e2xs2-e1xs1)-(e2-e1)xr1-

e2·Δxr，

(3)

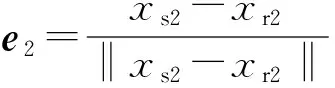
对于不同系统,接收机钟差dtr不一样,但可以选定某个系统的钟差作为参考,其它系统的钟差表示为系统间偏差,即dtr=dtr0+dtISB,而系统间偏差在短时间内很稳定,因此经过历元间差分后可以消掉,同样其它的码间偏差和频间偏差也可以由历元差进行消除[9]。

综上,对于不同系统不同频率上的周跳,可以列得形式相同的方程

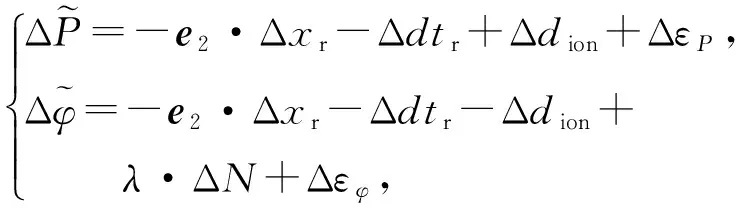
(4)

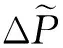
(5)

对于所有卫星的观测值,按照式(4)可形成周跳解算方程,由于所有参数均为线性,可以由最小二乘直接求解,得到周跳浮点值以后,再利用LAMBDA方法进行周跳整数值固定。

本文采用的非差非组合的周跳修复模型可适用于任意系统任意频率上的相位观测测,且对于各系统各频率上的周跳具有简单统一的观测方程形式,可方便加入新系统新频率上的周跳观测方程。此外,由于各类误差都作为参数进行估计,在一定程度上削弱了误差的影响,因此,非差非组合的周跳修复方法本质上和超宽巷-宽巷-窄巷逐级修复的方法是等价的。

2 惯性辅助周跳修复

惯性辅助周跳修复主要是利用惯性短时间内递推的高精度位移量,用来约束周跳修复方程中的位置变化量参数,改善周跳修复方程的条件数。此外,当卫星小于4颗时,由于加了惯性递推位移量的约束,周跳修复方程仍可以进行解算,这对于卫星信号遮挡严重的情况极为有用。

本文采用的是ECEF系下的PPP/SINS紧组合模型,如图1所示。

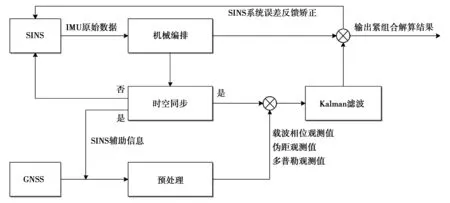
图1 PPP/SINS紧组合结构

GNSS和SINS的原始观测值共同输入到一个Kalman滤波器中,联合估计导航参数(位置、速度和姿态)、SINS系统误差以及PPP相关参数(对流层和模糊度),并且采用闭环修正技术,对SINS系统误差进行反馈校正。在发生周跳的时刻,利用校正以后的SINS观测值进行机械编排,由前一历元位置、速度和姿态作为初始条件,递推得到当前历元的高精度位置,从而得到相对于上一历元的位移量。PPP/SINS紧组合状态模型和观测模型,分别为

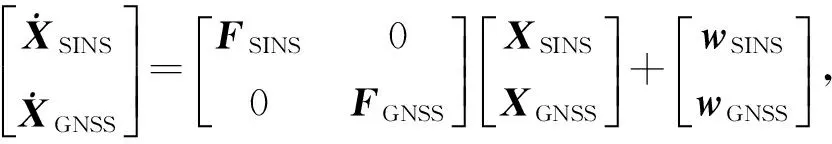
(6)

δz=HδX+η,

(7)

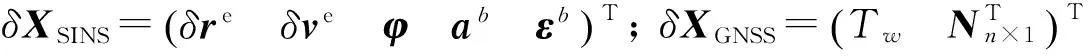
假设k-1时刻,PPP/SINS紧组合滤波完成,得到相应的位置xk-1及其方差P(xk-1),在k时刻发生周跳,此时,惯导利用已在线标定的IMU观测值进行机械编排,递推得到高精度的位置xk及其方差P(xk),由此可以得到k时刻的位置量及其方差:

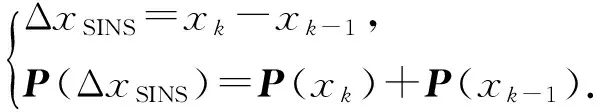
(8)

在得到惯导位移量ΔxSINS及其协方差阵P(ΔxSINS)后,将其作为虚拟观测值加入到周跳修复方程中一起进行最小二乘解算。当P(ΔxSINS)接近0时,等价于式(4)中的Δxr直接由ΔxSINS代入,不需要进行该位移参数的求解; 当P(ΔxSINS)趋于无穷时,等价于ΔxSINS对周跳修复方程没有任何贡献,即惯性不起任何辅助作用。P(ΔxSINS)值代表着ΔxSINS对周跳修复贡献的大小,由于相邻历元单点定位也可以求解得到位移量,因此,只有当ΔxSINS的精度优于单点定位精度时,惯性辅助周跳修复才有作用。当修复得到周跳值后,将其改正到原始相位观测值上,并再次使用周跳探测模块检验是否仍存在周跳,确保周跳修复的正确性。

值得一提的是,当不考虑ΔxSINS的方差时,直接将ΔxSINS代入方程(4)中,并且电离层变化量Δdion由预报值直接代入,此时方程(4)只存在钟差变化量和周跳参数,而钟差可以采用星间单差消除,此时周跳修复的几何模型就退化为无几何模型,可以直接获取周跳值ΔN.

3 实验测试与结果分析

为了验证惯性辅助PPP快速重新收敛和周跳修复的效果,本文采用了一组车载和一组机载实验的数据。两组数据均采用Novatel公司的SPAN-FASA组合导航设备,FASA是一款战术级别的光纤陀螺惯导,其陀螺零偏小于0.75 deg/h. 图2示出了两组数据的可视卫星数以及相应的PDOP值。

图2 可视卫星数以及PDOP值

两组数据观测条件较好,车载数据时长约为2.7 h,机载数据时长约为4.3 h,GPS观测数据采样率为1 Hz,IMU观测数据采样率为200 Hz,GPS卫星数基本在9～11颗,PDOP均值在2.0附近,利用GPS差分求解流动站坐标,均为固定解,可以作为PPP/SINS组合定位结果的参考值。本文通过人为地在GPS观测数据上引入周跳与中断来分析惯性辅助PPP定位的性能。从GPS观测数据起点开始,每隔20 min模拟20 s的中断,并在所有卫星的L1和L2观测值上引入随机的周跳值,由于模拟的周跳值已知,因此可以用来评估周跳修复的正确性。

3.1 SINS辅助PPP快速重新收敛的性能分析

对该上述模拟数据进行PPP和PPP/SINS紧组合正向滤波数据处理,并以GPS差分结果做为参考真值,得到的定位误差如图3所示。从图中可以看出,由于数据中断以及全部卫星发生周跳,PPP需要重新初始化,位置精度受到影响,其误差序列存在较长时间的收敛,而PPP/SINS紧组合可以在一定程度上加快模糊度的收敛,从而提高定位精度。在加入惯导辅助后,车载数据的定位精度从(0.408,0.465,0.938) m提高到(0.319,0.225,0.628) m,机载数据的定位精度从(0.597,0.639,0.922) m提高到(0.546,0.488,0.540) m.从精度统计的结果来看,高程分量精度改善较为明显。这是因为在PPP/SINS紧组合中,由于航向角难以估计,且垂直分量的重力通过水平角误差投影到水平面,导致紧组合中,平面位置精度要差于高程精度,但中断收敛以后,紧组合的位置精度主要取决于PPP,因而平面仍是优于高程精度。

加入SINS辅助后,PPP定位之所以能够加快收敛,主要是SINS提供的短时间内高精度的预报位置信息,对重新初始化的模糊度起到了约束作用。如图3所示,在首次初始化时,PPP和PPP/SINS紧组合的浮点模糊度收敛速度是一样的,在开始阶段,SINS的状态也处于滤波收敛状态,它不能给PPP提供准确的约束信息。而在GPS数据中断时,由于SINS的状态已收敛,系统误差也已经过在线标定,SINS机械编排递推的位置精度较高,从而可以用来约束浮点模糊度,加快浮点模糊度的收敛,图3中可以看到,车载和机载数据在加入SINS辅助后,能够加速重新初始化阶段浮点模糊度的收敛速度。

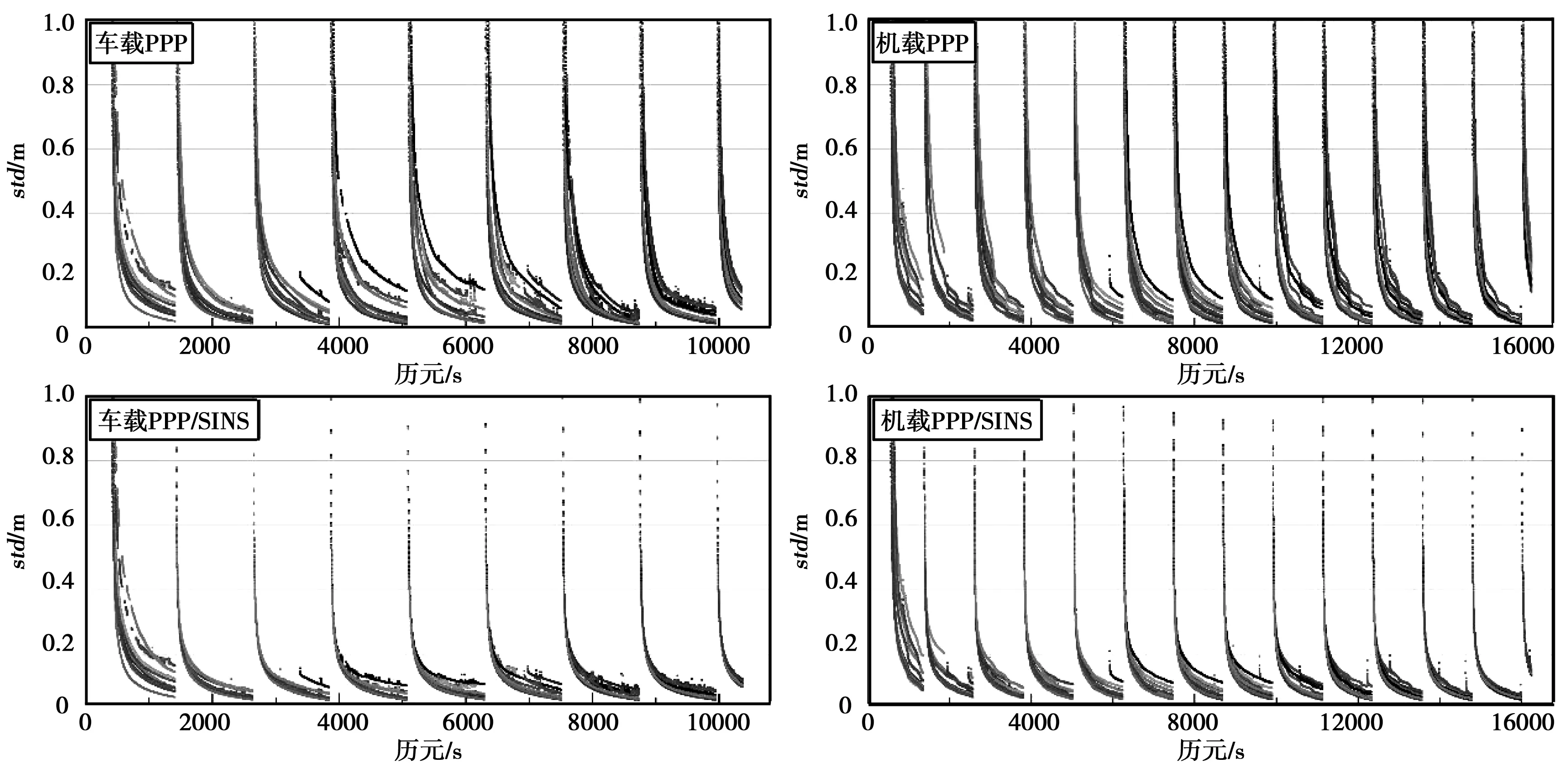
图3 模糊度标准差收敛情况

3.2 PPP/SINS紧组合周跳修复

采用本文提出的基于几何模式的PPP/SINS紧组合周跳修复算法,对两组数据进行周跳修复,其中车载数据共有8处中断,机载数据共有13处中断,修复结果如表1所示。

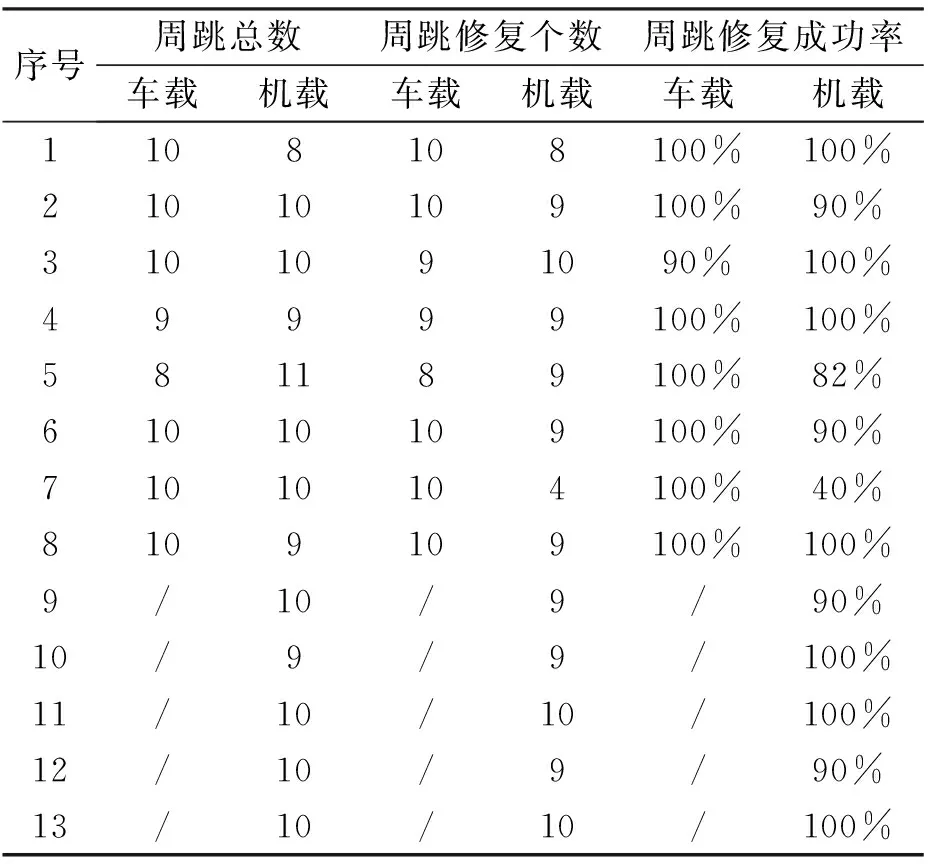
表1 周跳修复结果统计

车载数据的第3处中断有1颗卫星修复失败,其余处全部修复成功,成功率较高。机载数据有多处未能100%的成功修复周跳,其中第7处中断,只有4颗卫星修复成功,成功率只有40%,其余卫星按照模糊度重置的方式进行处理,连续跟踪的相位观测数小于PPP定位的必要观测数5,因此,定位结果出现明显波动,如图4中黑框所示。而其它中断处成功修复的卫星至少有8颗以上,对结果不会产生影响。机载数据的周跳修复效果不如车载数据,主要原因是飞机的速度远远大于地面车辆的速度,空间位置变化较大,导致电离层难以预报,同时,惯导递推的误差也较大,因此,机载数据更加难以修复周跳。

图4示出了加入惯性辅助以及周跳修复前后的位置误差对比。

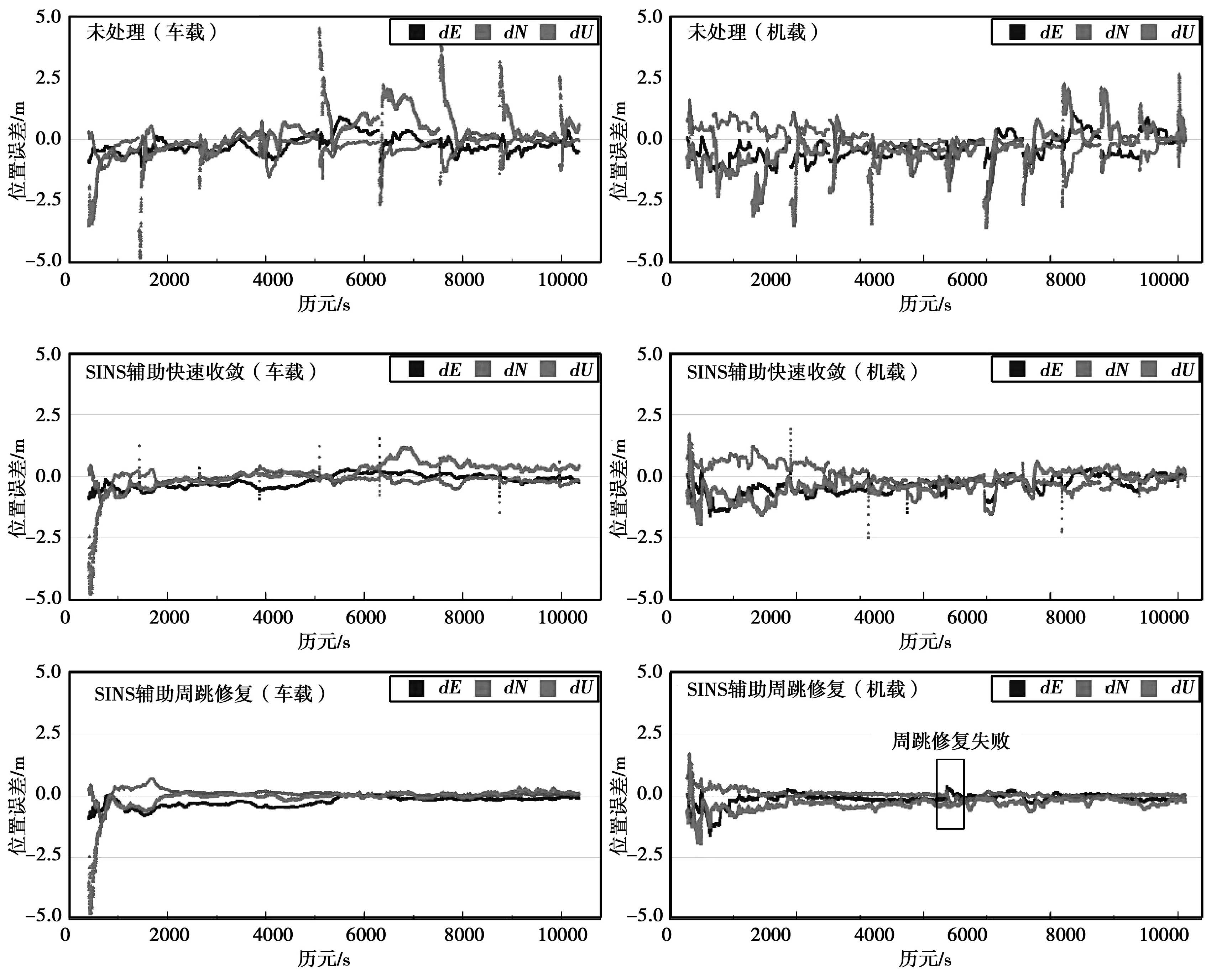
图4 周跳修复前后PPP/SINS紧组合定位结果

车载数据周跳修复成功后,整体较为平稳,位置精度逐步提高,机载数据在第7处中断上,未能成功修复足够多的卫星,导致位置误差较大,而其余周跳修复处定位精度均较好。总体而言,由于加入了惯导以后,即使周跳未能成功修复,位置精度仍能保持在较好的水平,且收敛较快,当周跳修复后,能够提高PPP/SINS定位定姿的精度。

统计了PPP/SINS收敛以后的位置、速度和姿态精度,如表2所示。

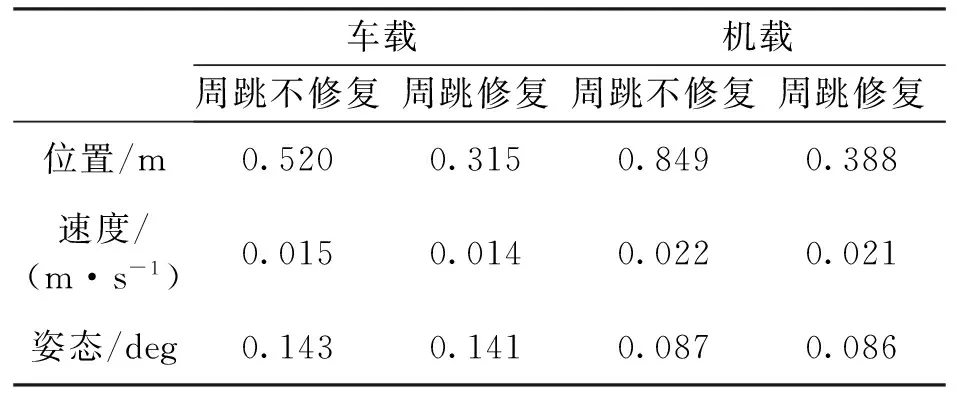
表2 周跳修复前后的PPP/SINS紧组合结果统计

周跳修复前后,位置精度改善比较明显,分别从0.520 m、0.849 m提高到了0.315 m、0.388 m,精度改善了39.4%和54.3%.而速度和姿态基本没有变化,在PPP/SINS紧组合中,速度和姿态估计的贡献主要来源于惯导的加计和陀螺观测量,短时间的中断不会产生明显的影响,而位置精度主要依靠GPS伪距和相位观测值,因此,周跳修复主要提高了PPP/SINS紧组合的定位精度。

4 结束语

针对复杂环境下的PPP定位,本文采用PPP/SINS紧组合方式,给出了惯性辅助周跳修复的几何模型,该模型基于非差非组合观测量,操作方便,可适用于多频多系统PPP的周跳修复,而惯导信息作为虚拟观测量参与周跳方程解算,该方法利用短时间内惯导递推的高精度位置信息辅助PPP周跳修复与快速重新收敛。通过两组实验数据的处理,表明该方法可以较好地修复周跳,地面车载数据比机载数据具有更高的周跳修复成功率,在引入惯性辅助后,重新初始化阶段的定位精度收敛明显加速,当周跳修复后,定位精度整体保持稳定,相比于周跳不修复的定位精度提高了39.4%和54.3%.此外,短时间中断的周跳修复与否,对速度和姿态影响不大。

致谢: 感谢武汉大学测绘学院朱锋博士对本文数据处理的相关建议。

[1] LI X, GE M, DAI X,etal. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635.

[2] LI X, ZHANG X, REN X,etal. Precise positioning with current multi-constellation global navigation satellite systems: GPS, GLONASS, Galileo and BeiDou[J]. Scientific reports, 2015, 5.

[3] GENG J, MENG X, Dodson A H,etal. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning[J]. Journal of Geodesy, 2010, 84(12): 705-714.

[4] CAI C, LIU Z, XIA P,etal. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity[J]. GPS solutions, 2013, 17(2): 247-260.

[5] 王振杰,聂志喜,欧吉坤. 一种基于 TurboEdit 改进的 GPS 双频观测值周跳探测方法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1017-1021.

[6] 柴艳菊,阳仁贵,张宝成. 动态 PPP 定位中周跳自动探测与处理策略[J]. 地球物理学报, 2014, 57(5): 1433-1439.

[7] ZHANG X H, LI X X. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing[J]. GPS Solutions, 2012, 16(3): 315-327.

[8] ZHAO Q, SUN B, DAI Z,etal. Real-time detection and repair of cycle slips in triple-frequency GNSS measurements[J]. GPS Solutions, 2015, 19(3): 381-391.

[9] YE S, LIU Y, SONG W,etal. A cycle slip fixing method with GPS+GLONASS observations in real-time kinematic PPP[J]. GPS Solutions, 2016, 20(1): 101-110.

[10]Li Z, Gao J, Wang J. Inertial aided cycle slip detection and repair for PPP/INS tightly coupled navigation[J]. The Journal of Navigation, 2016, 69(6): 1357-1378.

[11]刘帅,孙付平,张伦东, 等. INS 辅助周跳修复以实现精密单点定位瞬时重新收敛[J]. 中国惯性技术学报, 2015: 607-614.

[12]韩厚增,王坚,李增科. GPS/INS 紧组合的 INS 辅助周跳探测与修复[J]. 测绘学报, 2015, 44(8): 848-857.