基于高分值加权的改进阴影匹配定位算法研究

夏景平,胡辉,颜瑜军,欧敏辉

(华东交通大学 信息工程学院,江西 南昌330013)

0 引 言

随着全球卫星导航系统(GNSS)的不断发展,卫星定位已成为人们日常定位最主要的手段之一。然而在高楼密集、高楼间距离短的“城市峡谷”环境中,由于建筑物对卫星信号的遮挡、反射和衍射,会导致多径干扰、信号衰减、非视距信号(NLOS)被接收和几何精度因子(GDOP)变大,使得接收机存在较大定位误差甚至不能定位[1]。

针对“城市峡谷”环境中GNSS接收机不能定位或存在固有过街精度低的问题,Groves[2]提出基于3D城市地图的GNSS-阴影匹配(SM)算法,该算法利用3D城市模型和卫星仰角、方位角信息来预测不同位置的卫星可见性,并与实际位置GNSS接收机观测到的卫星可见性进行匹配来定位,仿真表明SM算法能够实现城市环境下米级的过街精度。Groves、Wang L[3]将SM算法首次用于实测环境,实测结果表明，使用该算法的GNSS接收机能识别出人行道和街道,但模板没有考虑卫星NLOS信号接收情况。Wang L等[4-6]进一步通过引入衍射模型来改善SM算法的匹配模板,在预测卫星可见性中引入固定的衍射模型,对统计模板进行了细分,并赋予不同的匹配分值,在智能手机上的测试结果表明,使用改善模板的定位误差相对于以前模板减少了9.4%,但定位精度提高不大。在“城市峡谷”中,卫星信号被玻璃、金属材质建筑反射会产生较强的NLOS信号,同时由于LOS信号被用户的身体、树木或者路过的行人遮挡,也可能衰减很大后被接收机接收,仅通过简单信噪比(SNR)阈值并不能有效区分LOS/NLOS信号。Wang L[7]通过对LOS信号的SNR数据进行统计建模,获得不同SNR条件下的LOS信号概率,并通过建筑边界信息、接收机位置和卫星仰角、方位角预测不同位置的LOS信号概率,来构建概率统计模板,并使用粒子滤波(PF)将概率统计模板用于行人运动下动态定位,改进的SM模板一定程度地提高了过街精度。2014年Wang Lei[8]提出了动态SM改进算法,在伦敦两条街道四条不同实验路线的实验表明,SM/KF和SM/PF组合算法相比单SM算法可以平滑位置误差,但定位精度改善不大,其中SM/PF组合算法效果更好。综上可知,SM算法存在固有SNR观测误差导致定位结果不准,同时PF算法对动态SM算法的有一定的平滑滤波作用,在一定程度上提高SM算法定位精度。针对以上问题,本文提出了基于高分值加权的改进SM定位算法。

1 基于高分值加权改进的SM定位算法

在“城市峡谷”环境中,由于建筑物分布特征不一致,在街道的不同位置建筑物对卫星信号的遮挡程度不同,接收的卫星信号也有较大差别。此时,用户可以通过星历计算卫星位置,结合周围的建筑模型来预测卫星的可见性;同时,接收机接收的卫星信号能观测卫星的可见性,对比预测和观测卫星可见性结果计算用户位置。SM算法流程如图1所示[9]，实现步骤如下：

图1 SM算法流程图

步骤一：初始化定位。由于初始化定位只为了得到用户较低精度的定位结果P0,尽管城市峡谷环境下GPS单点定位存在一定的误差,但仍然满足算法需求。

步骤二：确定搜索区域。以初始位置P0为中心确定搜索区域,一般选用固定半径的圆或矩形区域,本文选用以街道宽度为边长的15 m×40 m矩形搜索区域,网格候选位置面积为1 m2.

步骤三：预测卫星可见性。在步骤二中确定的每一个候选位置上,利用卫星星历计算当前时刻卫星的仰角和方位角,并利用周围的3D建筑模型计算同一方位角下的建筑物边界仰角,若卫星仰角高于建筑物边界仰角,则预测卫星可见;反之,预测卫星不可见。

步骤四： 观测卫星可见性。通过接收机接收卫星的NMEA-0183格式数据可获取每颗卫星的SNR,若卫星信号经建筑物反射、衍射被接收机接收,其SNR较低,则该卫星观测不可见;反之,卫星观测可见。其中SNR阈值见实验数据。

步骤五：卫星可见性打分。在步骤三、四得到卫星预测和观测可见性结果的基础上,对二者进行模板匹配打分,匹配越准打分越高。对于高于15°截止仰角的卫星,SM打分模板如图2所示,即观测和预测相同得分为1,不同得分为0.在候选位置对每颗卫星打分后,得到所有卫星可见性匹配总分值,其计算公式为

(1)

式中: fp(j)为候选位置j的最终得分值; fs(i,j)为卫星i对候选位置j的打分值; n为大于10°截止仰角的卫星颗数。

图2 SM打分模板图

步骤六：定位解算。由步骤五卫星打分模板可知,在卫星预测和观测准确的情况下,高分值所在的候选位置更接近真实位置,而打分最高的候选位置通常不只一个,对于计算得到的K个最高分值点,采用K最近邻点(KNN)算法得到SM的定位结果,简称KNN-SM算法,其计算公式为:

(2)

(3)

在实际情况中,存在卫星SNR经验阈值观测卫星可见性有误的情况,即最高分值点不一定更接近真实位置。此时引入次高分值加权来计算SM最终位置,一般最高分值所在的位置离真实位置更近,可信度更高,其权重更大。计算公式如下:

(4)

(5)

2 PF算法

本文在基于高分值加权的改进SM定位结果的基础上,使用PF算法对定位结果进行滤波,其基本实现步骤如下:

(6)

(7)

j=1,2,…,m,

(8)

(9)

步骤六:状态估计输出。通过更新后的粒子状态和权重,加权统计得到系统当前状态:

(10)

步骤七:判断算法是否结束。若是,则退出算法;否则返回步骤二。

3 实验结果分析

实验位于华东交通大学北区31栋与32栋之间的峡谷场景,实景图如图3所示,其中峡谷长度为50m,宽度为15m.利用全站仪测量建筑物顶点坐标,建立了如图4所示的3D建筑物轮廓模型。本文实验平台基于UbloxNEO-M8N接收机,前期在空旷场景和图5所示的城市峡谷场景同时采集卫星数据,分析数据可知峡谷中的NLOS信号强度明显低于空旷场景中的LOS信号,统计大量数据后取38dB作为SNR阈值来观测卫星的可见性[9]。

本文在图3所示的城市峡谷中选取了D108、D114、D120和D126共4个静态点进行SM定位实验,在Google地图上显示如图6所示。为了便于分析,以D120点采集数据为例来进行分析,其坐标为(28°44'52.7327"N,115°51'42.4182"E,45.12m),数据采集时间为2016年12月18日17:09:14-17:11:14.实验过程中通过GPS星历和3D建筑模型预测D120点的卫星可见性,可知10、25和31号卫星预测可见,其他卫星预测不可见。

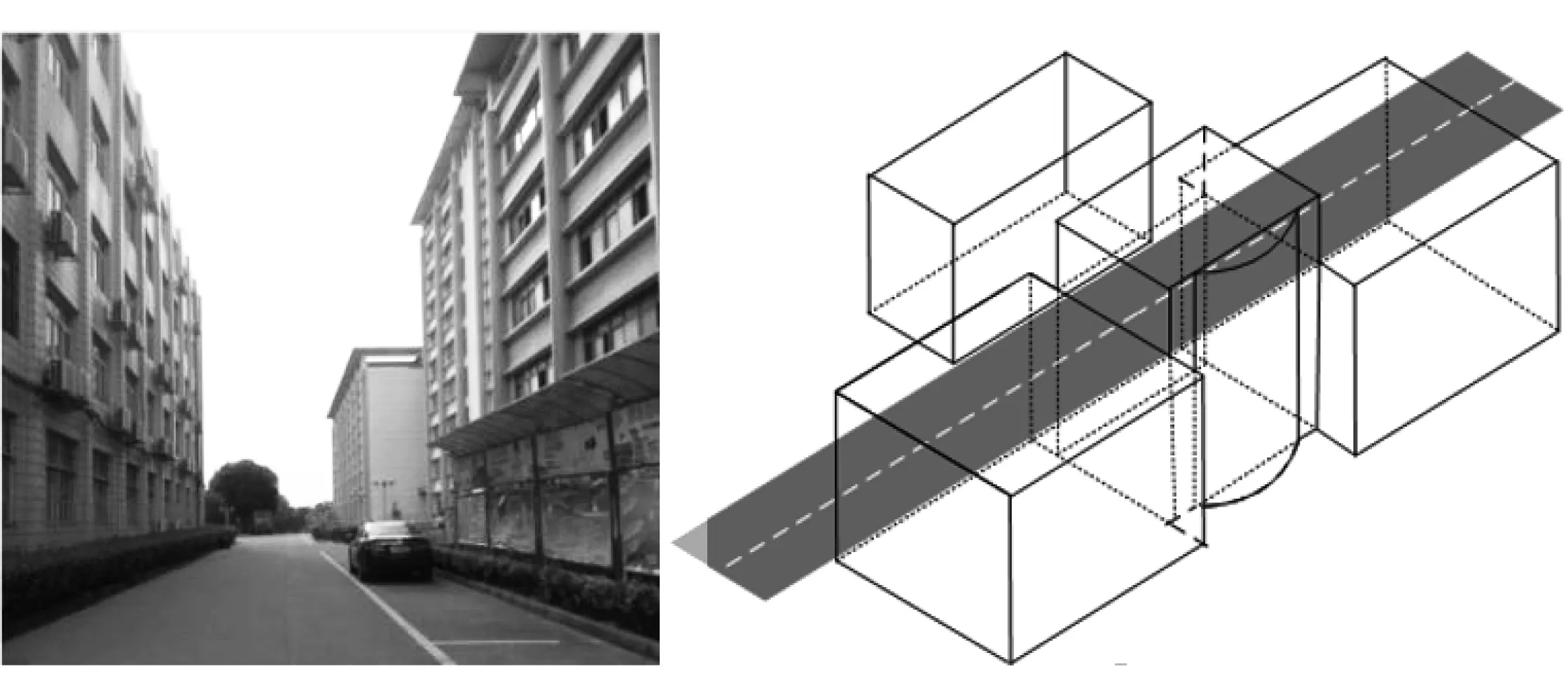
图3 城市峡谷实景图 图4 3D建筑模型

图5 城市峡谷中静态实验点图 图6 城市峡谷中实验路径

实验过程中接收机接收到预测可见卫星的SNR如图7所示,对于大于15°较低仰角的31卫星,由于卫星信号穿过电离层造成了较大的衰减,同时受到树木、车辆、行人的遮挡等,其SNR在大量时刻低于38dB阈值而被观测为不可见。而较高仰角的10号卫星也受到附近车辆、行人的影响,在第27～29s、68s时SNR低于阈值,SM模板匹配分值如图8所示。

由图8可知,黄色为最高分值,即所有的7颗卫星预测和观测结果均匹配。蓝色“+”号标记为真实位置,红色“*”号标记为改进SM定位结果,绿色“×”号标记为KNN-SM定位结果,可知改进SM定位结果更接近真实位置。这是由于10号卫星信噪比观测不准,在600个候选位置中仅有7个最高分值,通过最高分值位置得到KNN-SM定位结果存在较大偏差,而此时次高分值的个数较多且分布均匀,平均位置更接近真实位置。

图7 10/25/31号卫星SNR变化特性 图8 10号卫星第68 s的SM模板匹配分值

对于预测不可见的卫星,图9所示第83s的14号卫星信号被建筑物反射到达接收机,其SNR等于阈值38 dB观测可见,SM模板匹配分值如图11所示。

如图10可知,最高分值所在的黄色区域偏离真实位置,而次高分值个数较多,且分布相对集中于真实位置,红色“*”号标记的改进SM定位结果相对于绿色“×”号标记的KNN-SM定位结果更接近真实位置。

图9 14/32号卫星SNR变化特性 图10 14号卫星第83 s的SM模板匹配分值图

图11、图12为KNN-SM和改进SM定位结果对比,可知改进SM定位精度相对于KNN-SM在沿街和过街方向均有所提高,在卫星SNR观测可见性有误的异常点处,SM定位误差突然增大,通过高分值加权改进后误差有一定程度的降低。统计改进的SM在沿街方向定位误差均值为1.08 m,相对于KNN-SM的1.28 m降低了15.6%,过街方向定位误差均值为0.32 m,相对于KNN-SM的2.32 m降低了82.6%,有效改善了GPS过街方向误差偏大的问题。

图11 沿街方向定位误差对比 图12 过街方向定位误差对比

同理,对D108、D114和D120点进行误差统计,并对4个位置的误差统计平均如表1所示,GPS过街方向平均定位误差为10.05 m明显高于沿街方向的0.88 m,无法满足城市环境中的精确定位需求。改进SM在沿街方向平均定位误差为2.07 m,相对于KNN-SM的2.95 m降低了30%;在过街方向平均定位误差为0.88 m,相对于KNN-SM的2.64 m降低了66.7%.

为了进一步测试改进SM定位算法性能,本文在华东交通大学15与16楼之间进行动态实验,实验路径如图6所示。起点D178坐标为28°44'52.17875" N,115°51'41.74564" E,45.25 m,终点D78坐标为28°44'52.72285" N,115°51'43.54570" E,45.12 m,D178到D78的距离为110.33 m.Ublox NEO-M8N接收机采集GPS数据的时间为2016年11月3日11:46:23-11:48:00.

表1 D120静态实验点位置误差统计

如图13、图14所示,接收机进入峡谷前GPS定位结果相对稳定,第30 s左右进入峡谷时发生较大突变,过街方向尤为剧烈。由于峡谷环境中建筑物结构类似,SM定位驻留使沿街方向的定位误差呈锯齿形,但由于接收机接收SNR观测卫星可见性不准,定位结果存在少量突变点。可知,改进SM定位算法在沿街和过街方向定位误差均低于KNN-SM,PF-改进SM定位算法对SM定位突变点有一定的滤波作用,其定位精度最高,误差对比如表2所示。

图13 沿街方向定位误差 图14 过街方向定位误差

位置误差沿街方向误差过街方向误差最大值/m平均值/m均方根最大值/m平均值/m均方根KNN-SM19.437.514.947.252.761.68改进SM17.085.624.584.291.941.6KF-改进SM13.894.944.124.231.911.53UKF-改进SM13.494.644.044.221.91.53PF-改进SM11.184.283.194.031.781.44

本文对改进SM定位结果分别使用KF、UKF和PF进行滤波对比,其定位误差如图15、16所示,可知改进SM在滤波前后定位误差趋势保持一致,在SM定位突变的时刻,三种滤波算法起到了一定的平滑作用。由于PF不受噪声类型和模型的影响,其滤波性能较KF和UKF更优,定位误差对比统计如表2所示:KF-改进SM和UKF-改进SM算法效果近似,较改进SM定位精度略有提高,而PF-改进SM算法的定位性能最好,在沿街和过街方向定位误差分别为4.28 m和1.78 m,相对于加权SM的5.62 m和1.94 m,分别降低了23.8%和8.2%.

图15 沿街方向误差 图16 过街方向误差

4 结束语

本文在分析KNN-SM定位算法中SNR观测卫星可见性存在误差的基础上,提出了基于高分值加权改进的SM定位算法,并使用PF对动态场景下的改进SM定位结果进行滤波。该算法考虑实际环境中NLOS信号强度可能高于LOS信号,导致SM打分不准,通过引入次高分值加权来提高定位精度。同时,将该算法应用到动态场景中,并使用PF算法对定位结果进行优化。实验结果表明:静态和动态场景下该算法的平均定位误差为2.45 m和4.64 m,相对于传统SM定位算法的3.96 m和5.95 m,分别降低了38.1%和21.9%.

[1] HSU L T, GU Y L, KAMIJO S. NLOS correction/exclusion for GNSS measurement using RAIM and city building models[J]. Sensors, 2015, 15(7):17329-17349.

[2] GROVES P D. Shadow matching: A new GNSS positioning technique for urban Canyons[J]. Journal of Navigation, 2011, 64(3):417-430.

[3] GROVES P, WANG L, ZIEBAR M. Shadow matching improved GNSS accuracy in urban Canyons[J]. GPS World, 2012, 23(2)：14-18，27-29.

[4] WANG L, GROVES P D, ZIEBART M K. GNSS shadow matching: Improving urban positioning accuracy using a 3d city model with optimized visibility scoring scheme[J]. Navigation-Journal of The Institute of Navigation, 2013, 60(3):195-207.

[5] WANG L, GROVES P D, ZIEBART M K. Shadow matching: Improving smartphone GNSS positioning in urban environments[J]. Lecture Notes in Electrical Engineering, 2013( 245):613-621.

[6] WANG L, GROVES P, ZIEBART M. Urban positioning on a smartphone: Real-time shadow matching using GNSS and 3D city models[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2013:1606-1619.

[7] WANG L. Smartphone shadow matching for better cross-street GNSS positioning in urban environments[J]. Journal of Navigation, 2015, 68(3):411-433.

[8] WANG L. Kinematic GNSS shadow matching using a particle filter[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2014.

[9] 胡辉, 颜瑜军, 欧敏辉. 一种基于EKF的GPS/SM组合定位算法[J]. 全球定位系统, 2016, 41(2):7-13.

[10]周瑞, 李志强, 罗磊. 基于粒子滤波的WiFi行人航位推算融合室内定位[J]. 计算机应用, 2016,36(5):1188-1191.